catalogue
2.2 advantages and disadvantages of Bloom filter
1, Bitmap
1.1 bitmap concept
Bitmap is a bit to represent a state. A bit has two states: 0 and 1. 0 can represent a state and 1 can represent a state. It is usually used to judge whether a data store exists. For example, to judge whether a data is saved, it can be represented by a bitmap. The corresponding bit of the data is 1, which means it is saved, and the corresponding bit is 0, which means it is not saved. If you want to know whether a number exists, you can directly find the status of the corresponding bit of the number.
Note: the bitmap does not save data, but the saved state.
1.2 application of bitmap
Bitmap is suitable for massive data without duplication. Because bits are used, the occupied space will be relatively small.
- Quickly find whether a data is in the collection
- Sorting + de duplication.
- Find the intersection, union, etc. of two sets
- Disk tags in the operating system
Advantages: small space
OK: only shaping can be processed
1.3 implementation of bitmap
We use an array to hold the shaping, one shaping 4 bytes. One byte 8 bits. So one element of the array occupies 32 bits.
- Find the corresponding bit of data
Save data to a location 1 and delete data to a location 0. The search data has been saved. You need to find the corresponding bit of the number. How to find it?
1. First find the index in which the data is saved in the array.
2. Find out which subscript the data is in.
//Get the bits of the data in the array_ Which subscript in bit int index = num / 32;//Array one element 32 bits //Get which bit to save the array in int pos = num % 32;
- Place a position 1
Bitwise OR operation '|' can be used. By bit or, 1 is 1 and all 0 is 0.
In this way, you need to get a corresponding number of 1 and other bits of 0. You can use the shift operation to shift 1 to the left pos bit.
Move the current element of the array by bit or up 1 to the left pos bit, and the corresponding position will be 1.
//Save the data to the corresponding position 1
void set(size_t num){
if (num > _bitcount){
return;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Set this position to 1, press bit or operate
_bit[index] |= (1 << pos);
}- Set a location to 0
Bitwise and operation '&' can be used. By bit and, all 1 is 1, and 0 is 0.
In this way, you need to get a corresponding number of 0 and other bits of 1. You can use the shift operation to shift 1 to the left pos bit and then reverse it by bit. By biting the current element of the array with the previous number, the corresponding position is 1.
//Delete the data and change the corresponding position to 0
void reset(size_t num){
if (num > _bitcount){
return;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Bitwise and operation
_bit[index] &= (~(1 << pos));
}- Find the status of the corresponding bit of the data
You can use bitwise &, with the corresponding bit of 1 and other bits of 0 and the upper array element
Press bit or no, the corresponding bit is 0 and other bits are 1. Will change the state of other bits.
//Check that the data exists
bool test(size_t num){
if (num > _bitcount){
return false;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Bitwise OR operation
return (_bit[index] & (1 << pos)) != 0;
}- Complete code
#pragma once
//The bitmap and bloom filter are only the existence of empty data. A bit 01 status, 0 does not exist and 1 exists. No data saved
#include<vector>
class bitset{
public:
bitset(size_t bitcount){
_bitcount = bitcount;
_bit.resize(bitcount / 32 + 1);//One int, one 32-bit. The open space size is always increased by 1, and the remainder may not be 0. Complement the remainder.
}
//Save the data to the corresponding position 1
void set(size_t num){
if (num > _bitcount){
return;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Set this position to 1, press bit or operate
_bit[index] |= (1 << pos);
}
//Delete the data and change the corresponding position to 0
void reset(size_t num){
if (num > _bitcount){
return;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Bitwise and operation
_bit[index] &= (~(1 << pos));
}
//Check that the data exists
bool test(size_t num){
if (num > _bitcount){
return false;
}
//Get the bits of the data in the array_ Which subscript in bit
int index = num / 32;//Array one element 32 bits
//Get which bit to save the array in
int pos = num % 32;
//Bitwise OR operation
return (_bit[index] & (1 << pos)) != 0;
}
private:
std::vector<int> _bit;
size_t _bitcount = 0;//Total number of bits
};2, Bloom filter
2.1 concept of Bloom filter
From the above, we know that the disadvantage of bitmap is that it can only record whether to save integer data. Bloom filter aims at this disadvantage and can also record other types of data except integers.
The bottom layer of Bloom filter is realized by bitmap, and other types are transformed into shaping by hash function. However, there is a disadvantage. Different data may be converted to the same value through hash function. For example, "abcd" and "aadd" hash functions of string type add up the ASCII code values of all characters, and the two strings will get the same value.
This will lead to misjudgment, and the saved data will not be saved. However, the unsaved data will not be saved when the value calculated by the hash function is the same as the integer value of one of the saved values.
This misjudgment can not be substantially solved, but some methods can be used to reduce the misjudgment.
The bloom filter uses multiple hash functions to obtain multiple values from the values to be saved, and sets multiple positions in the bitmap to 1. When the measurement is not available, it is necessary to check whether all positions are 1.
For example:
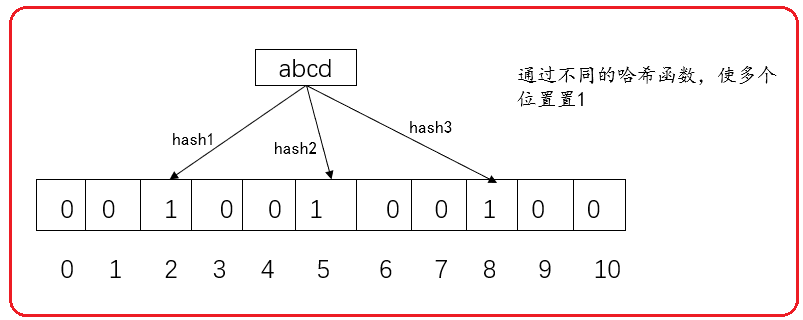
2.2 advantages and disadvantages of Bloom filter
advantage:
The time complexity of adding and querying elements is O(K), (K is the number of hash functions, which is generally small), which is independent of the amount of data.
There is no relationship between hash functions, which is convenient for hardware parallel computing.
Bloom filter does not need to save the function itself, which has great advantages in some occasions with strict confidentiality requirements.
Space saving and efficient
Disadvantages:
Misjudgment exists and deletion is not supported.
2.3 realization
- Parameters of Bloom filter
bitset _bloom;//bitmap size_t _count = 0;//Number of data
- Initialization of Bloom filter
bloomfilter(size_t num)
:_bloom(num * 5)//The length is too small to filter and cannot be too large. It is best to multiply by 5
, _count(0)
{}
The number of bitmaps can be determined by the number of data. As we know above, a data corresponds to multiple bits. If the number of bits of the bitmap of the bloom filter is exactly the number of data, the bloom filter will soon be full. The data is not easy to save and can not play the role of filtering. But the number of digits is too large and the space is too large. Therefore, it was studied that it is best to open up 5 times the number of elements.
- Insertion of Bloom filter
After the insertion is transformed into shaping by hash function, the corresponding position 1 is in the bitmap.
void insert(const K& num){
//First turn to plastic surgery
int index1 = KToInt1()(num) % _bloom.bitcount();//Leave all digits to prevent cross-border
std::cout << index1 << std::endl;
int index2 = KToInt2()(num) % _bloom.bitcount();
std::cout << index2 << std::endl;
int index3 = KToInt3()(num) % _bloom.bitcount();
std::cout << index3 << std::endl;
//Place the corresponding position 1
_bloom.set(index1);
_bloom.set(index2);
_bloom.set(index3);
}- Lookup of Bloom filter
After the search is transformed into shaping by hash function, check whether each bit is 1 in the bitmap. If one bit is not 1, it does not exist.
//As long as one bit is 0, it does not exist
bool IsBloomFilter(const K& num){
int index1 = KToInt1()(num) % _bloom.bitcount();//Leave all digits to prevent cross-border
if (!_bloom.test(index1)){
return false;
}
int index2 = KToInt2()(num) % _bloom.bitcount();
if (!_bloom.test(index2)){
return false;
}
int index3 = KToInt3()(num) % _bloom.bitcount();
if (!_bloom.test(index3)){
return false;
}
return true;
}- Deletion of Bloom filter
The bloom filter does not support deletion because different data may be set to 1 on multiple bits through multiple hash functions. However, different data may have the same position through multiple bits of different hash functions.
For example:
If abcd is deleted, the position of the corresponding bitmap 2 will be set to 0, and the corresponding aadd will be detected as nonexistent, which actually exists. Therefore, there can be no deletion operation.
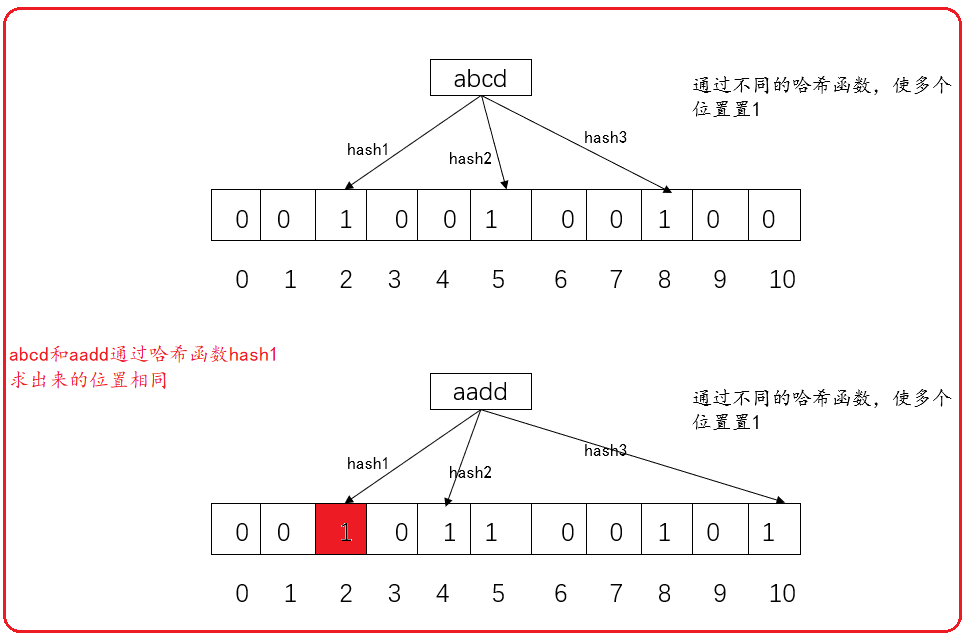
Note: bloom filter reduces misjudgment by adding multiple positions to 1 through multiple hash functions, and does not solve misjudgment.
Complete code
#pragma once
//Bloom filter is implemented with bitmap
#include"bitset.h"
#include<string>
template<class T>
struct KeyToInt1{
T& operator()(const T& k){
return k;
}
};
template<>
struct KeyToInt1<std::string>
{
size_t operator()(const std::string& s){
if (s.size() == 0){
return 0;
}
size_t hash = 0;
for (size_t i = 0; i < s.size(); i++){
hash *= 131;
hash += s[i];
}
return hash;
}
};
template<class T>
struct KeyToInt2{
T& operator()(const T& k){
return k;
}
};
template<>
struct KeyToInt2<std::string>
{
size_t operator()(const std::string& s){
if (s.size() == 0){
return 0;
}
size_t hash = 0;
for (size_t i = 0; i < s.size(); i++){
hash *= 65599;
hash += s[i] ;
}
return hash;
}
};
template<class T>
struct KeyToInt3{
T& operator()(const T& k){
return k;
}
};
template<>
struct KeyToInt3<std::string>
{
size_t operator()(const std::string& s){
if (s.size() == 0){
return 0;
}
int magic = 63689;
size_t hash = 0;
for (size_t i = 0; i < s.size(); i++){
hash *= magic;
hash += s[i];
magic *= 378551;
}
return hash;
}
};
//KToInt is a function that converts K type into int, converts a data into multiple shaping, and multiple bits save the state of a data
template<class K, class KToInt1 = KeyToInt1<K>, class KToInt2 = KeyToInt2<K>, class KToInt3 = KeyToInt3<K>>
class bloomfilter{
public:
bloomfilter(size_t num)
:_bloom(num * 5)//The length is too small to filter and cannot be too large. It is best to multiply by 5
, _count(0)
{}
void insert(const K& num){
//First turn to plastic surgery
int index1 = KToInt1()(num) % _bloom.bitcount();//Leave all digits to prevent cross-border
std::cout << index1 << std::endl;
int index2 = KToInt2()(num) % _bloom.bitcount();
std::cout << index2 << std::endl;
int index3 = KToInt3()(num) % _bloom.bitcount();
std::cout << index3 << std::endl;
//Place the corresponding position 1
_bloom.set(index1);
_bloom.set(index2);
_bloom.set(index3);
}
//As long as one bit is 0, it does not exist
bool IsBloomFilter(const K& num){
int index1 = KToInt1()(num) % _bloom.bitcount();//Leave all digits to prevent cross-border
if (!_bloom.test(index1)){
return false;
}
int index2 = KToInt2()(num) % _bloom.bitcount();
if (!_bloom.test(index2)){
return false;
}
int index3 = KToInt3()(num) % _bloom.bitcount();
if (!_bloom.test(index3)){
return false;
}
return true;
}
private:
bitset _bloom;
size_t _count = 0;//Number of data
};