Handwritten HashMap? So hard, the interview has been rolled to this extent?
The first time I saw this interview question was in the article of an Offer harvester boss who was inconvenient to be named:
This... I was numb at that time. We all know that the data structure of HashMap is array + linked list + Red and black tree. Is this the rhythm of tearing the red and black tree by hand?
Later, after sorting out some Facebook, it was found that Kwai Kwai appeared frequently in the quick interview. The analysis of this question should be in the quick question database. Since it happens frequently, you can't tear the red and black tree by hand - I think most interviewers can't tear it out. If they don't tear the red and black tree, this question is still a little saved. Look down slowly.
Recognize hash table
HashMap is actually the implementation of hash table in data structure in Java.
Hash table essence
Hash table is also called hash table. Let's take a look at the definition of hash table:
Hash table is a data structure that can be accessed directly according to the value of key.
It's like someone looking for a third in the company. The little sister at the front desk is good at pointing to the station in the corner.
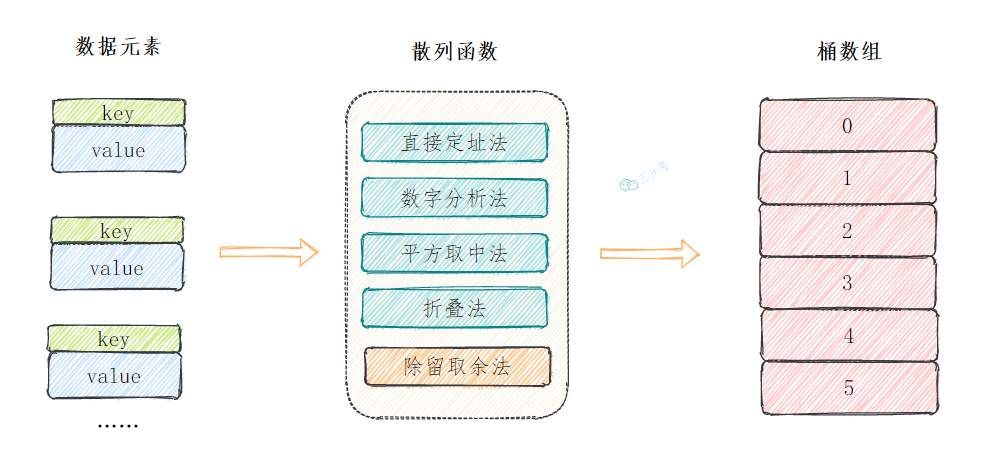
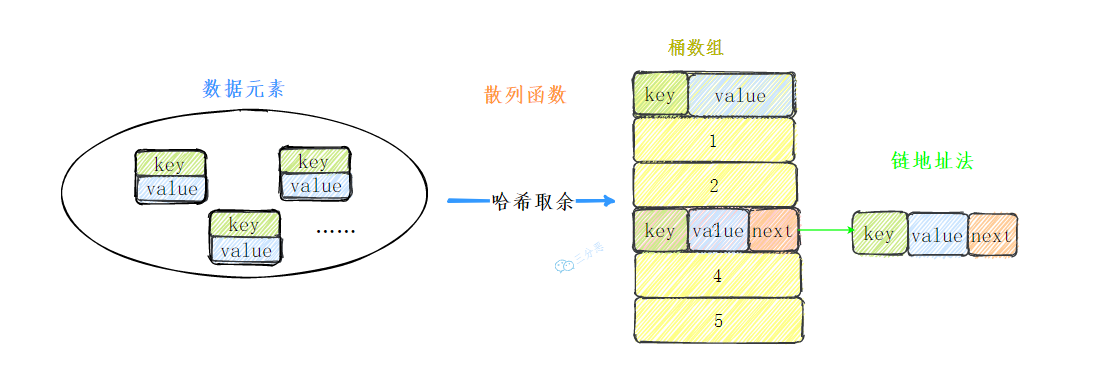
In short, a hash table consists of two elements: a bucket array and a hash function.
- Bucket array: one row of stations
- Hash function: the third is in the corner
Bucket array
We may know that there is a kind of basic data structure linear table, and there are two kinds of linear table, array and linked list.
In the hash table data structure, the data structure for storing elements is an array. Each unit in the array can be imagined as a Bucket.
If several programmers are assigned stations: egg, Xiong Da, Niu Er and Zhang San, we observe that these names are more distinctive. The last word is a number. We can extract it as the key code. In this way, they can be assigned to the corresponding numbered station. If they are not assigned, let it be empty first.
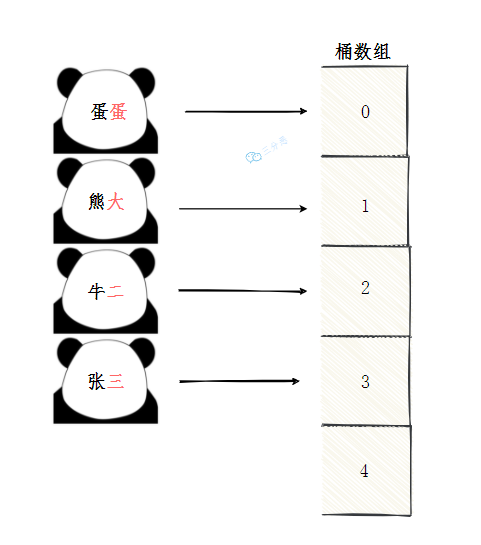
So what is the time complexity of finding / inserting / deleting in this case? Obviously, they are all O(1).
But we are not gourd babies. We can't all call them 1234567. If the newcomer is Nangong Daniu, how can we assign him?
This introduces our second key element, hash function.
Hash function
We need to establish a mapping relationship between the element and the bucket array. This mapping relationship is a hash function, which can also be called a hash function.
For example, we have a bunch of irregular names Zhuge iron and steel, Liu Huaqiang, Wang situ and Zhang quandan... We need to calculate which station these names should be assigned to through the hash function.
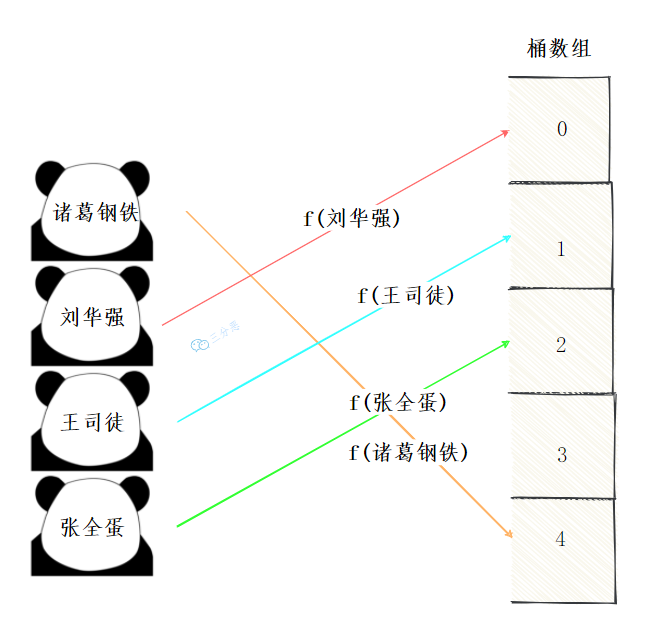
Hash function construction
Hash function is also called hash function. If the key of our data element is an integer or can be converted to an integer, we can obtain the mapping address through these common methods.
- direct addressing Directly map to the corresponding array position according to the key, for example, 1232 is placed at the position of subscript 1232.
- Digital analysis Take some numbers of the key (such as tens and hundreds) as the mapping position
- Square middle method Take the middle bits of the key square as the mapping position
- Folding method Divide the key into several segments with the same number of bits, and then take their superposition and as the mapping position
- Division method H (key)=key%p (p < = n), the keyword is divided by a positive integer p not greater than the length of the hash table, and the remainder is the hash address, which is the most widely used hash function construction method.
In Java, the Object class provides a default hashCode() method, which returns a 32-bit int integer, which is actually the storage address of the Object in memory.
However, this integer must be processed. Among the above methods, the direct addressing method can be excluded, because we can't build such a large bucket array.
And the hash address we finally calculated should be within the length of the bucket array as far as possible, so we choose the division and retention method.
Hash Collisions
Ideally, each data element is calculated by the hash function and falls in the position of its unique bucket array.
However, the reality is usually unsatisfactory. Our space is limited, and the best hash function can not completely avoid hash conflict. The so-called hash conflict is that different key s fall to the same subscript after being calculated by the hash function.
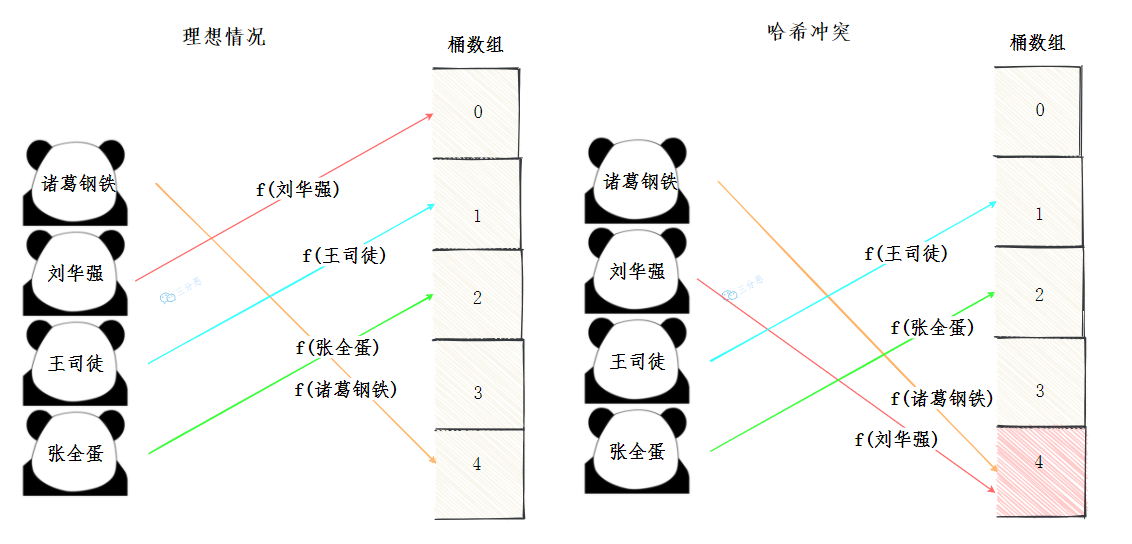
Now that there are conflicts, we have to find ways to solve them. Common ways to solve hash conflicts are:
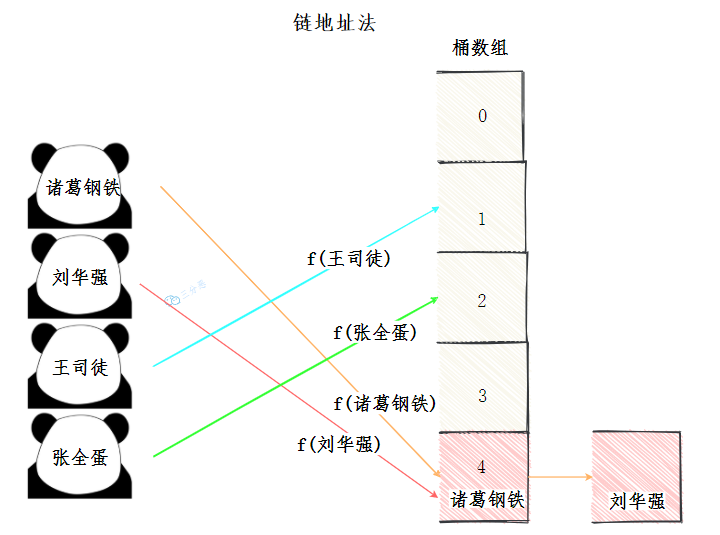
Chain address method
It is also called zipper method. It looks like pulling another linked list on the bucket array. Put the elements with hash conflict into a linked list. When looking up, traverse the linked list from front to back and find the corresponding key.
Open address method
The open address method is simply to find a free position in the bucket array for the conflicting elements.
There are many ways to find free locations:
- Line detection method: start from the conflicting location, judge whether the next location is free in turn until the free location is found
- Square detection method: start from the conflicting position x, add 1 ^ 2 positions for the first time, and add 2 ^ 2... For the second time until a free position is found
- Double hash function exploration method
......
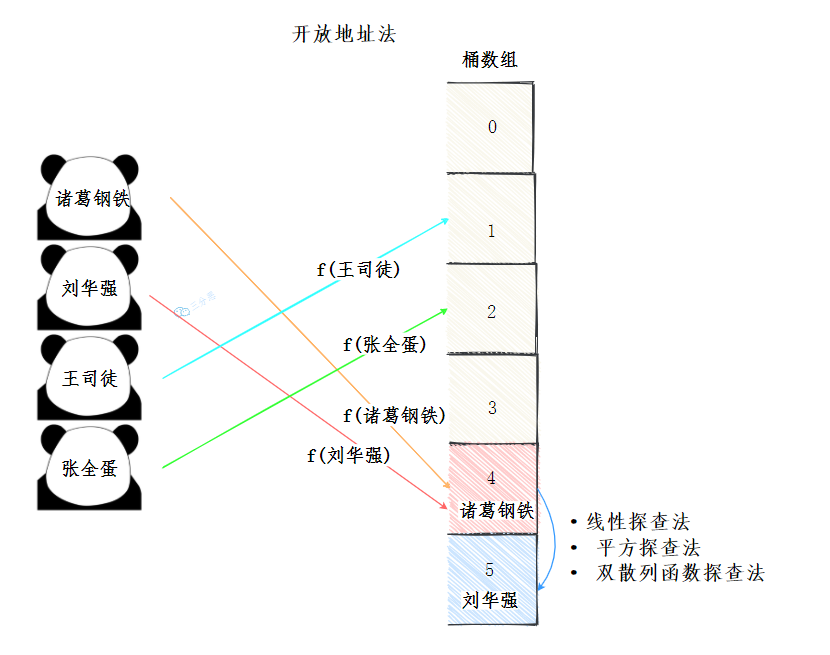
double hashing
Construct multiple hash functions. In case of conflict, replace the hash function until a free location is found.
Establish public overflow area
Establish a public overflow area and store the conflicting data elements in the public overflow area.
Obviously, next we will use the chain address method to solve the conflict.
Well, that's all for the introduction of hash table. I believe you have a deep understanding of the essence of hash table. Next, enter the coding time.
HashMap implementation
The simple HashMap we implemented is named ThirdHashMap. First determine the overall design:
- Hash function: hashCode() + division and remainder method
- Conflict resolution: chain address method
The overall structure is as follows:
Internal node class
We need to define a node as the carrier of specific data. It not only carries key value pairs, but also serves as the node of the single linked list:
/**
* Node class
*
* @param <K>
* @param <V>
*/
class Node<K, V> {
//Key value pair
private K key;
private V value;
//Linked list, successor
private Node<K, V> next;
public Node(K key, V value) {
this.key = key;
this.value = value;
}
public Node(K key, V value, Node<K, V> next) {
this.key = key;
this.value = value;
this.next = next;
}
}Member variable
There are mainly four member variables, in which the bucket array is used as the structure for loading data elements:
//Default capacity
final int DEFAULT_CAPACITY = 16;
//Load factor
final float LOAD_FACTOR = 0.75f;
//Size of HashMap
private int size;
//Bucket array
Node<K, V>[] buckets;Construction method
There are two construction methods: nonparametric construction method, bucket array default capacity, and bucket array capacity specified with parameters.
/**
* Parameterless constructor, set the default capacity of bucket array
*/
public ThirdHashMap() {
buckets = new Node[DEFAULT_CAPACITY];
size = 0;
}
/**
* A parameterized constructor that specifies the bucket array capacity
*
* @param capacity
*/
public ThirdHashMap(int capacity) {
buckets = new Node[capacity];
size = 0;
}Hash function
Hash function is the hashCode() and array length remainder we mentioned earlier.
/**
* Hash function, get address
*
* @param key
* @return
*/
private int getIndex(K key, int length) {
//Get hash code
int hashCode = key.hashCode();
//And bucket array length remainder
int index = hashCode % length;
return Math.abs(index);
}put method
I use a putval method to complete the actual logic, because this method will also be used in capacity expansion.
General logic:
- Get element insertion location
- The current position is empty. Insert directly
- The position is not empty. There is a conflict. Traverse the linked list
- If the element key is the same as the node, overwrite it. Otherwise, the new node is inserted into the linked list header
/**
* put method
*
* @param key
* @param value
* @return
*/
public void put(K key, V value) {
//Determine whether capacity expansion is required
if (size >= buckets.length * LOAD_FACTOR) resize();
putVal(key, value, buckets);
}
/**
* Stores the element in the specified node array
*
* @param key
* @param value
* @param table
*/
private void putVal(K key, V value, Node<K, V>[] table) {
//Get location
int index = getIndex(key, table.length);
Node node = table[index];
//The inserted position is empty
if (node == null) {
table[index] = new Node<>(key, value);
size++;
return;
}
//If the insertion position is not empty, it indicates a conflict. Use the chain address method to traverse the linked list
while (node != null) {
//If the key s are the same, they are overwritten
if ((node.key.hashCode() == key.hashCode())
&& (node.key == key || node.key.equals(key))) {
node.value = value;
return;
}
node = node.next;
}
//The current key is not in the linked list. Insert the header of the linked list
Node newNode = new Node(key, value, table[index]);
table[index] = newNode;
size++;
}Capacity expansion method
General process of capacity expansion:
- Create a new array with twice the capacity
- Rehash the elements of the current bucket array to a new array
- Set the new array as the bucket array of map
/**
* Capacity expansion
*/
private void resize() {
//Create an array of buckets with twice the capacity
Node<K, V>[] newBuckets = new Node[buckets.length * 2];
//Rehash the current element to a new bucket array
rehash(newBuckets);
buckets = newBuckets;
}
/**
* Rehash current element
*
* @param newBuckets
*/
private void rehash(Node<K, V>[] newBuckets) {
//map size recalculation
size = 0;
//Brush all the elements of the old bucket array into the new bucket array
for (int i = 0; i < buckets.length; i++) {
//Null, skip
if (buckets[i] == null) {
continue;
}
Node<K, V> node = buckets[i];
while (node != null) {
//Put elements into a new array
putVal(node.key, node.value, newBuckets);
node = node.next;
}
}
}get method
The get method is relatively simple. I get the address through the hash function. Here, I omit the judgment of whether there is a linked list and directly look up the linked list.
/**
* Get element
*
* @param key
* @return
*/
public V get(K key) {
//Get the address corresponding to the key
int index = getIndex(key, buckets.length);
if (buckets[index] == null) return null;
Node<K, V> node = buckets[index];
//Lookup linked list
while (node != null) {
if ((node.key.hashCode() == key.hashCode())
&& (node.key == key || node.key.equals(key))) {
return node.value;
}
node = node.next;
}
return null;
}Full code:

test
The test code is as follows:
@Test
void test0() {
ThirdHashMap map = new ThirdHashMap();
for (int i = 0; i < 100; i++) {
map.put("Hua Qiang Liu" + i, "Are you sure this melon is cooked?" + i);
}
System.out.println(map.size());
for (int i = 0; i < 100; i++) {
System.out.println(map.get("Hua Qiang Liu" + i));
}
}
@Test
void test1() {
ThirdHashMap map = new ThirdHashMap();
map.put("Liu Huaqiang 1","Man, are you sure this melon is cooked?");
map.put("Liu Huaqiang 1","I must have your melon cooked!");
System.out.println(map.get("Liu Huaqiang 1"));
}You can run by yourself and see the results.
summary
Well, here we have a simple HashMap to achieve, and the interview Kwai is no longer afraid of handwritten HashMap.
Kwai: Interviewer: really? I don't believe it. I want you to write a red and black tree version
Of course, we also find that the O(1) time complexity operation of HashMap is in the case of less conflicts, and the simple hash remainder is certainly not the optimal hash function; After the conflict, the linked list is pulled too long, which also affects the performance; In fact, there are thread safety problems in our capacity expansion and put
However, in reality, we don't have to consider so much, because Master Li has written it for us, and we just call it.
reference resources:
[1] Data structure and algorithm