1. Semi-folded insertion sort:

• Half insertion sort is actually an optimization of direct insertion sort. Half search is used to find the location to insert, then move the elements, and finally insert.
• Idea analysis:
• Define low as the first position of the ordered part and high as the last position of the ordered part. Through the method of half-search, update low and high until low > high, then high+1 is the position we want to insert.
• The direct insertion sort is to move the data at each comparison, while the semi-insertion sort is to move the element of high+1 position to the last element j of the ordered part through a cycle once after finding the insertion position, and finally insert the value value of this time to the position of high+1.
• The code is implemented as follows:

package www.first;

import java.util.Scanner;

public class HalfInsertSort {
    public static void halfInsertSort(int[] arr){
        if(arr.length<=1||arr==null){
            return;
        }else{
            //i is the first element position of the disordered part
            for(int i = 1;i<arr.length;i++){
                //Store the values of disordered elements for easy comparison
                int value = arr[i];
                //The first element position of the ordered part
                int low = 0;
                //The last element position of the ordered part
                int high = i-1;
                while(low<=high){
                    int mid =(low+high)/2;
                    if(value<arr[mid]){
                        high = mid-1;
                    }else{
                        low = mid+1;
                    }
                }
                //At this point, the insertion location is found, high+1, and the element is moved.
                //Move the elements in the high+1~j position one bit back
                int j = i-1;
                for(;j>high;j--){
                    arr[j+1] = arr[j];
                }
                //After the loop, j is high at this point
                //Assign the high+1 position to our value
                arr[j+1] = value;
            }
        }
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String str = scanner.nextLine();
        String[] s = str.split(" ");
        int[] array = new int[s.length];
        for(int i = 0;i<s.length;i++){
            array[i] = Integer.parseInt(s[i]);
        }
        halfInsertSort(array);
        for(int i:array){
            System.out.print(i+" ");
        }
    }
}

The results are as follows: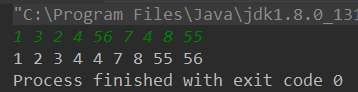

• The time complexity and space complexity of semi-insertion sort are the same as that of direct insertion sort, and it is also a stable sort algorithm.
• Comparisons between semi-insertion sort and direct insertion sort:
  I randomly generated 100,000 ordered data and 100,000 disordered data. Let's look at the results: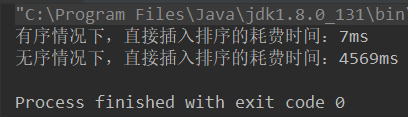
  
  
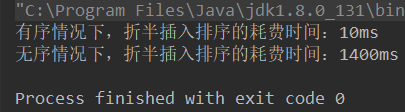
  It can be seen that the semi-insertion sort is better than the direct insertion sort in the case of disorder, but in the case of near-ordered, the direct insertion sort is better than the semi-insertion sort, because the direct insertion only uses comparison once.

2. Hill Ranking:

• Thought analysis: Hill sorting reduces the number of data exchanges and moves by dividing data into different groups, sorting each group first, when most of the data is in order, and then inserting and sorting all elements once.
• Code implementation:

public class ShellSort {
    public static void shellSort(int[] arr){
        if(arr.length<=1||arr==null){
            return;
        }else{
            int step = arr.length/2;
            while(step>=1){
                for(int i = step;i<arr.length;i++){
                    int value = arr[i];
                    int j = i-step;
                    for(;j>=0;j-=step){
                        if(value<arr[j]){
                            arr[j+step] = arr[j];
                        }else{
                            break;
                        }
                    }
                    arr[j+step] = value;
                }
                step/=2;
            }
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{1,2,5,6,8,2,3,5,2};
        shellSort(arr);
        for(int i:arr){
            System.out.print(i+" ");
        }
    }
}

The results are as follows: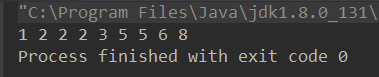

• Hill sorting is to insert elements according to asynchronous size. When the initial elements are out of order, the step size is the largest, and the number of elements in the insert sorting is very small. When the step size is 1, the elements are basically in order, and then insert sorting will greatly improve efficiency.
• The time complexity of Hill sort is O(nlogn) and the space complexity is O(1), but it is not a stable sort algorithm because the same elements may move in their respective insertion sort.
• The comparison of Hill sort with direct insert sort and half insert sort:
  Random generation of 100,000 pieces of data for three ways of sorting, the results are as follows: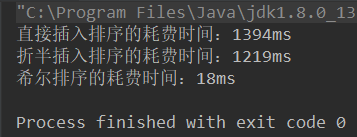
  
  It can be seen that Hill sort is much more efficient than direct insert sort.