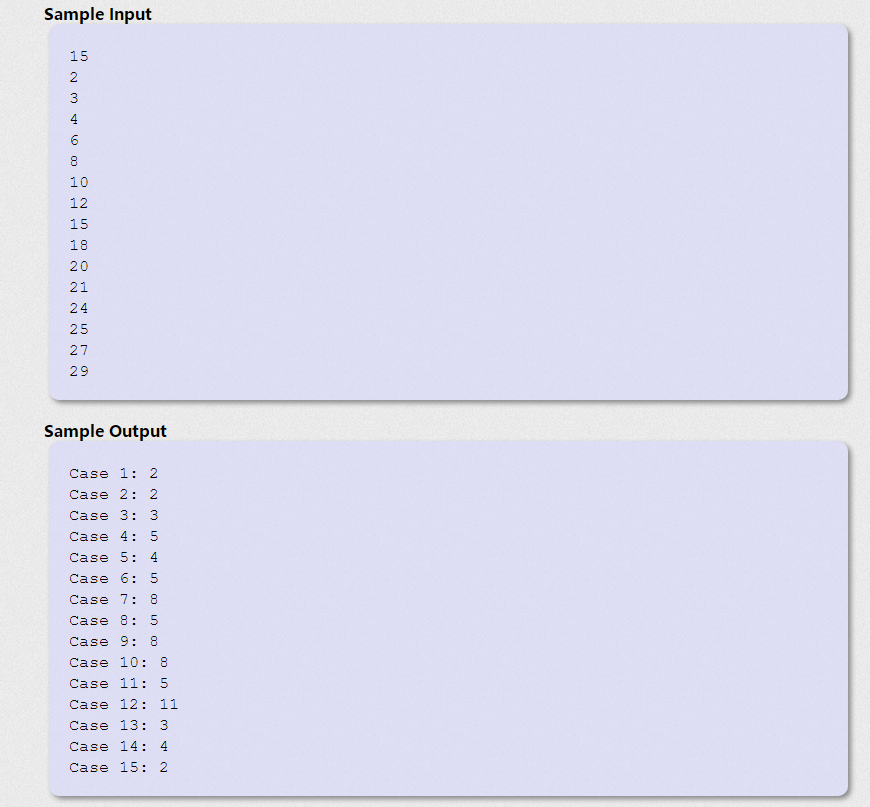
I began to look for the rule, and thought that the direct n-euler (n) + 1 was finished, but I found that it was not right because when n equals 8, the number of 6 was missed.
So Baidu asked how to write this question, alas... We also encounter the prime sieve and the unique decomposition theorem.
But this time I saw a big guy's talk is really good!

When I looked at the solution, I found that it used high school independent events. But I think it should be like this after careful consideration, because we know that any number can be represented by the product of prime numbers, and the events of each prime number are independent, so the types need to be multiplied, but note that when m==n, the same kind is added here, so one needs to be subtracted. Then we need to pay attention to that if n is not decomposed to 1, then there will be a prime number, so ans needs ans*=3. Finally, we need to pay attention to 1, because 1 is not a prime number, so we need to add a 1 to the final answer.

#include<map>
#include<list>
#include<ctime>
#include<queue>
#include<deque>
#include<cmath>
#include<stack>
#include<string>
#include<cstdlib>
#include<cstring>
#include <iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
//ll gcd(ll a,ll b){
//   return b?gcd(b,a%b):a;
//}
//ll QP(ll x,ll n,ll Mod){
//     ll res=1;
//     while(n){
//       if(n&1){
//         res=(res*x)%Mod;
//       }
//       x=(x*x)%Mod;
//       n>>=1;
//     }
//       return res;
//}
//bool is_prime(int x)
//{
//    if (x < 2 || x % 2 == 0)return false;
//    for (int i = 3; i*i < x;i+=2)
//    if (x%i == 0)return false;
//    return true;
//}
//Euler function template used to find the number of 1--n and n coprime 
//ll eular(ll n){
//	 ll ans=1;
//	 for(ll i=2;i*i<=n;i++)
//	 	if(n%i==0){
//	 		n/=i;ans*=i-1;
//	 		while(n%i==0) n/=i,ans*=i;
//		 }
//	    if(n>1) ans*=n-1;
//	    return ans;
//}
//Sieve prime template
const int N = 1e7 + 10;
int pri[700010], k;
bool Isprime[N];
void prime()
{
    k = 0;
    memset(Isprime, true, sizeof(Isprime));
    Isprime[1] = false;
    for(int i = 2 ; i < N ; i++)
    {
        if(Isprime[i])
        {
            pri[k++] = i;
            for(int j = 2 ; i * j < N ;j++)
                Isprime[i * j] = false;
        }
    }
}//Prime number selection
int main()
{
	prime();
    ll T,n,g=1,ans,count;
    scanf("%lld",&T);
    while(T--){
    	ans=1;
    	scanf("%lld",&n);
    	for(int i=0;i<k;i++){//Decomposition number n
    		count=0;
    		 while(n%pri[i]==0){
    		   count++;
    		   n/=pri[i];
			 }
			 ans*=(2*count+1);
		}
		if(n!=1) ans*=3;//It shows that n does not reach 1 after decomposition, so there is a larger prime number.  
		printf("Case %lld: %lld\n",g++,ans/2+1); 
	}
  return 0;
}