catalogue
1. Description of single source shortest path problem
4. Specific code implementation
1. Description of single source shortest path problem
① Given weighted digraph G =(V,E). Where V is the set of all vertices in the graph. E is the set of all edges in the graph, and the weight of each edge is a nonnegative real number.
② A vertex in a given V is called a source.
③ Calculate the shortest path length from the source to all other vertices.
Dijkstra algorithm is the most representative greedy algorithm for solving single source shortest path problem.
2.Dijkstra algorithm idea
① Set the vertex set U, which represents the selected node, so the initialized U contains only the source node.
② Set a table, which records the minimum distance from the node outside u and within V to any node in U.
③ Constantly make greedy choices and select nodes that are not in the U set to join the set.
④ Whenever a node joins the set, the minimum distance from other nodes not joined to any point in U is updated.
⑤ When all nodes are added to U, the algorithm is completed.
doubt:
What does this have to do with the path after adding U? Even if it has something to do with Lu Jin, can you ensure that it is the shortest path?
We analyze from the first node joining U:
When we want to select the first node to join U, we can only select the node with path relationship with the source node.
If other nodes have no path relationship with the source node, the distance to the source node is infinite, so they can only wait to contact the source node through other nodes.
Among the nodes that have a path relationship with the source node at the beginning, we select the node with the shortest road strength to join U.
Why? Because the distance from this node to the source node must be the shortest.
For example, the distance from node a to the source node is 10, the distance from node b to the source node is 20, and the distance from other nodes to the source node is infinite. If a is not selected at this time, there are only two methods to select a later: either directly through b to the source node, or first through b's expansion node and then through b to the source node. The path length of both methods is at least 20 +, which is greater than 10. Therefore, it is best to add a to U, and the path from a to the source node is also the shortest.
For other nodes that are not expanded for the first time, the process is the same:
If you don't choose the shortest path to join U at this time, you can only choose another longer path.
This proves the correctness of Dijkstra algorithm.
3. Specific case analysis
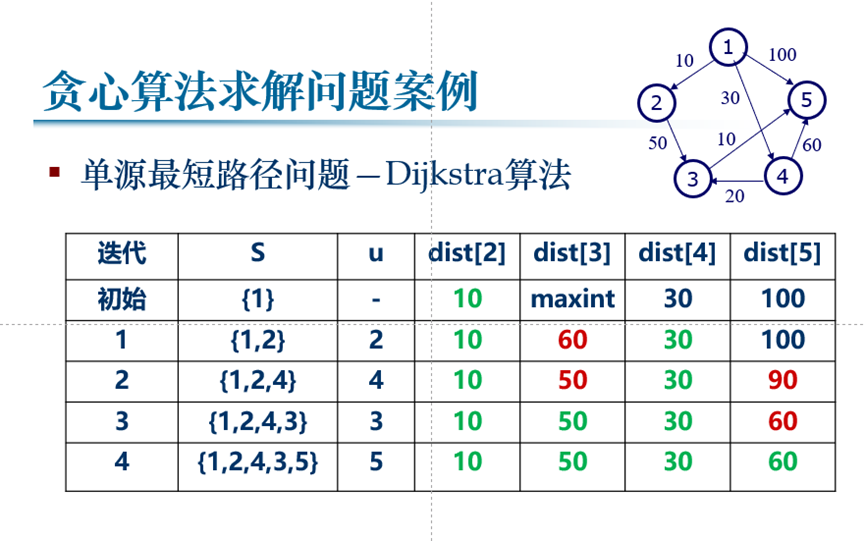
4. Specific code implementation
public class SingleSourceShortestPath {
public static void main(String[] args) {
//Number of nodes
int num = 5;
//Source node
int sourcev = 1;
/*
* 5 Nodes, but let the adjacency matrix be c[6][6]
* In this way, c[1][2] represents the distance from the first node to the second node, which is better understood
* Therefore:
* Because there is no node 0, the first row and column of the adjacency matrix are invalid and set to - 1
* Since the node itself is meaningless, the left to right diagonal of the adjacency matrix is invalid and set to - 1
*/
int[][] c = {{-1,-1,-1,-1,-1,-1},
{-1,-1,10,-1,30,100},
{-1,10,-1,50,-1,-1},
{-1,-1,50,-1,20,10},
{-1,30,-1,20,-1,60},
{-1,100,-1,10,60,-1}};
//result
int[][] result = dijkstra(num,c,sourcev);
for (int i = 1; i <= num; i++) {
System.out.print("node" + i + ":");
if(i == sourcev) {
System.out.println("This node is the source node!");
}else {
System.out.print("The shortest path to the source node is" + i + "->");
int index = result[0][i];
while(index != sourcev) {
System.out.print(index + "->");
index = result[0][index];
}
System.out.println(sourcev + ",Count Reg" + result[1][i]);
}
}
}
/**
*
* @param num Number of nodes
* @param c adjacency matrix
* @param sourcev Source node
* @return An array. Line 0 of the array represents the precursor node of the node, and line 1 of the array represents the distance from the source to the node.
*/
private static int[][] dijkstra(int num, int[][] c, int sourcev) {
int[][] prevANDdist = new int[2][num+1];
boolean[] isChosen = new boolean[num+1];
//initialization
for (int i = 1; i < prevANDdist[0].length; i++) {
if(i == sourcev) {
prevANDdist[0][i] = -1;
prevANDdist[1][i] = Integer.MAX_VALUE;
isChosen[sourcev] = true;
}else {
if(c[i][sourcev] != -1) {
prevANDdist[0][i] = sourcev;
prevANDdist[1][i] = c[i][sourcev];
isChosen[i] = false;
}else {
prevANDdist[0][i] = -1;
prevANDdist[1][i] = Integer.MAX_VALUE;
isChosen[i] = false;
}
}
}
//Because num-1 nodes other than the source node are added in turn, it is necessary to cycle num-1 times.
for (int i = 1; i <= num-1; i++) {
int tempv = 0;
int tempdist = Integer.MAX_VALUE;
//Select next node
for (int j = 1; j <= num; j++) {
if(isChosen[j]==false && prevANDdist[1][j]<tempdist) {
tempv = j;
tempdist = prevANDdist[1][j];
}
}
//Update the table after confirming who the next node is
isChosen[tempv] = true;
for (int j = 1; j <= num; j++) {
if(isChosen[j]==false && c[tempv][j] != -1) {
if(prevANDdist[1][tempv] + c[tempv][j] < prevANDdist[1][j]) {
prevANDdist[0][j] = tempv;
prevANDdist[1][j] = prevANDdist[1][tempv] + c[tempv][j];
}
}
}
}
return prevANDdist;
}
}2021/11/27
If you think it's helpful, please like it or collect it~