Linked list

1. Preface

C/C + + has its own data structure - array, which is easy to use, but it can't insert or delete elements at any position, so we need another data structure to realize this operation, so the linked list was born. The linked list supports insertion or deletion at any position, but can only access the elements in order. We can use a struct to represent the nodes of the linked list, which can store any data. Then we can use prev and next pointers to point to the front and rear nodes to form a common two-way linked list structure. In addition, in order to prevent the left and right ends or the access in the empty linked list from crossing the boundary, we usually establish two additional nodes, head and tail, to represent the head and tail of the linked list.

2. Code implementation

const int maxn=100100;

struct Node{
	int value;
	int prev,next;
}node[maxn];

int tot,head,tail;
int q;

int initialize(){
	tot=2;
	head=1;
	tail=2;
	node[head].next=tail;
	node[tail].prev=head;
}

int insert(int p,int val){
	q=++tot;
	node[q].value=val;
	node[node[p].next].prev=q;
	node[q].next=node[p].next;
	node[q].next=q;
	node[q].prev=p;
}

void remove(int p){
	node[node[p].prev].next=node[p].next;
	node[node[p].next].prev=node[p].prev;
}

Adjacency table

In many structures related to linked lists, adjacency list is a very important one. It is the general storage method of tree and graph structure.

In fact, adjacency table can be regarded as a structural set composed of "multiple data linked lists with index array". The data stored in such a structure is divided into several categories, and the data of each category constitutes a linked list. Each class also has a representative element, which is called the "header" of the linked list corresponding to the class. All "headers" form a header array as a random access index, so you can locate the linked list corresponding to a certain type of data through the header array.

When a new data node needs to be inserted, we can locate the linked list header of the category to which the new data node belongs through the header array head, and insert the new data in the header position.

In a digraph structure with n points and m edges, we can define the "category" of each edge as the starting point label of the edge. In this way, all edges are divided into n classes, and class X consists of "all edges starting from X". Through the header head[x], we can easily locate the linked list corresponding to class X, so as to access all edges starting from point X.

Let me draw a picture to make you better understand. (don't spray ugly words ~)

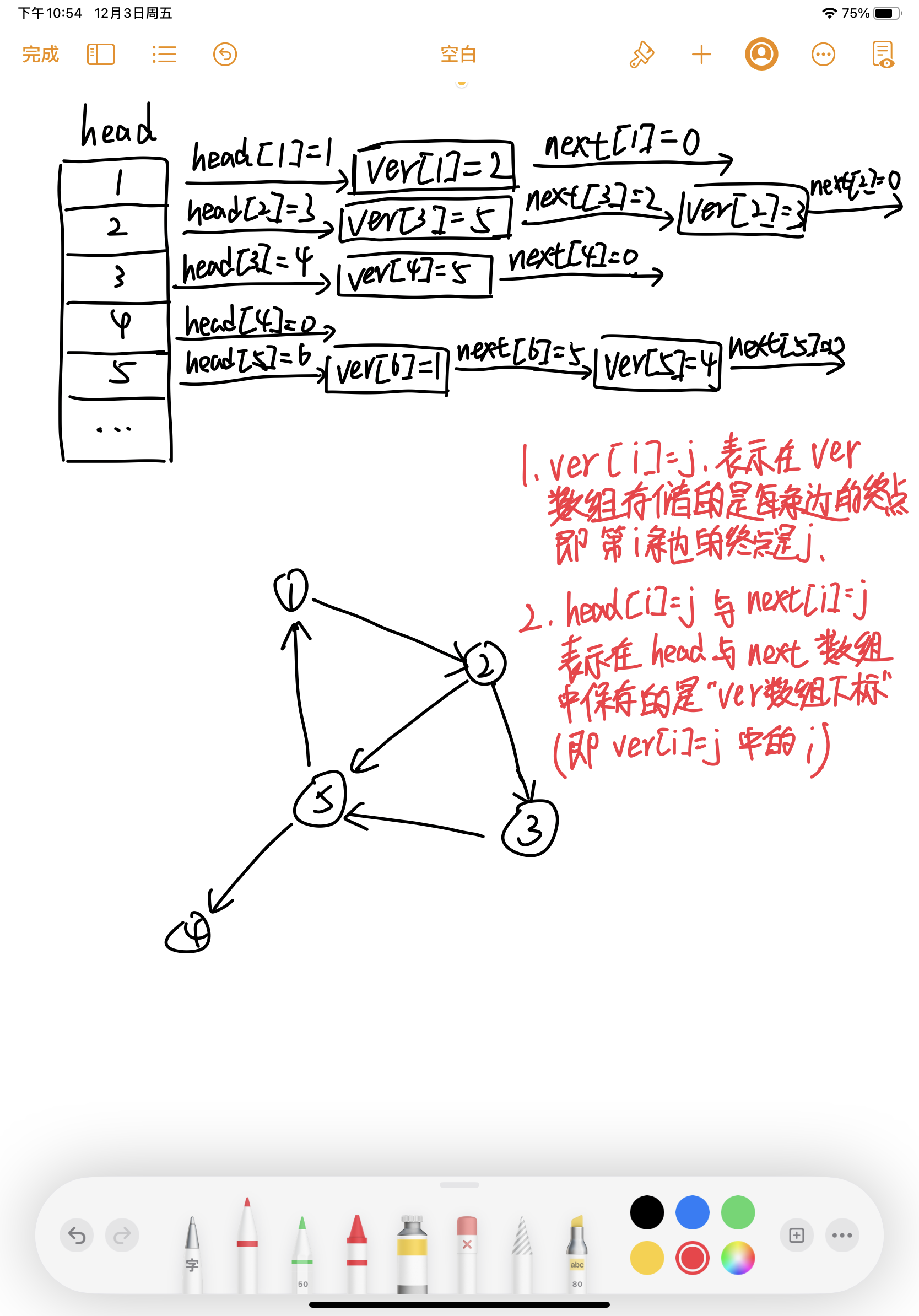
The specific code is as follows:

void add(int x,int y,int z){//Add the directed edge x, and the weight of y is z
    ver[++tot]=y;
    edge[tot]=z;
    next[tot]=head[x];
    head[x]=tot;
}

//Access all edges from x
for(int i=head[x];i;i=next[i]){
    int y=ver[i];
    int z=edge[i];
}

  For an undirected graph, we treat each undirected edge as two directed edges.

Similarly, we can implement it with struct, so that we can record points and use them better.

Code examples are as follows:

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;

struct Edge{
	int next;
	int edge;
	int ver;
}t[100100];

int tot,head[100100];

void add(int x,int y,int z){
	t[++tot].ver=y;
	t[tot].edge=z;
	t[tot].next=head[x];
	head[x]=tot;
}

int main(){
	int n;
	cin>>n;
	int x,y,z;
	for(int i=1;i<=n;i++){
		cin>>x>>y>>z;
		add(x,y,z);
	}
	for(int i=1;i<=n;i++){
		cout<<"point:"<<i<<endl;
		for(int j=head[i];j;j=t[j].next){
			y=t[j].ver;
			z=t[j].edge;
			cout<<y<<" "<<z<<endl;
		}
	}
}
/*
5
1 2 5
1 3 1
2 3 4
3 4 3
4 5 2
*/

Sample input:

5
1 2 5
1 3 1
2 3 4
3 4 3
4 5 2

Sample output:

point:1
3 1
2 5
point:2
3 4
point:3
4 3
point:4
5 2
point:5
              <-- (there should be no output here)

Then we can happily write the graph thesis