preface
Hello, I'm brother Xiong.
Today, I'll bring you a high-frequency interview question related to array. This question has been tested as an interview question by Internet companies such as IBM, Google and Goldman Sachs, that is, the 259 question on the force buckle - the sum of smaller three numbers and the 918 question on the collar buckle - the sum of three numbers is less than.
This paper mainly introduces three methods to solve this problem, such as sorting + binary search and sorting + collision pointer, for your reference and hope to be helpful to you.
Smaller sum of three
Given a length of n An array of integers and a target value target,Look for conditions that enable nums[i] + nums[j] + nums[k] < target Established triples i, j, k Number (0) <= i < j < k < n).

Examples and advanced
Problem solving ideas
It's easy to think of doing it through violent enumeration.
Solution 1: Violence Law
According to the meaning of the topic, traverse (three times) the whole array to find the solution that meets the conditions.
Show me the Code
C
int threeSumSmaller(int* nums, int numsSize, int target){
int cnt = 0;
for (int i = 0; i < numsSize - 2; ++i) {
for (int j = i + 1; j < numsSize - 1; ++j) {
for (int k = j + 1; k < numsSize; ++k) {
if (nums[i] + nums[j] + nums[k] < target) {
cnt++;
}
}
}
}
return cnt;
}
Complexity analysis
Time complexity: O(n^3), where n is the length of the array.
Space complexity: O(1), no additional storage space is opened up.
Operation results
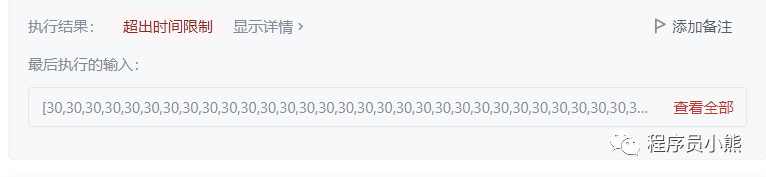
Force buckle operation results
Due to the violence method, the time complexity is O(n^3), and the time complexity is too high, resulting in timeout on the force buckle (not on the collar buckle).
Solution 2: sorting + binary search
When you encounter search related problems, it is easy to think of the binary search method to solve them. Because this problem does not explain that the array is orderly, you need to sort the array first, and then binary search.
give an example
Take num = [- 2,0,1,3], target = 2 as an example, as shown in the figure below.
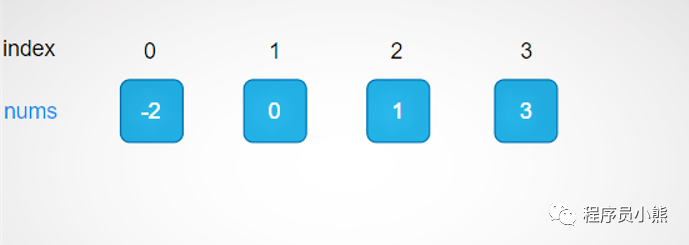
example
Since nums itself is ordered, there is no need to sort.
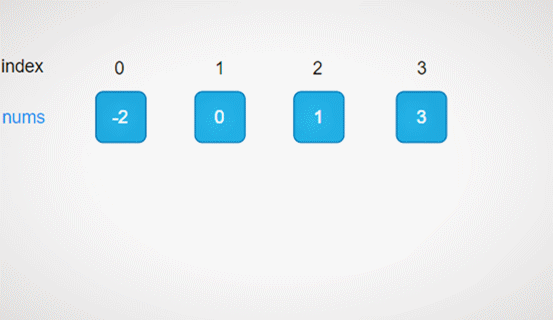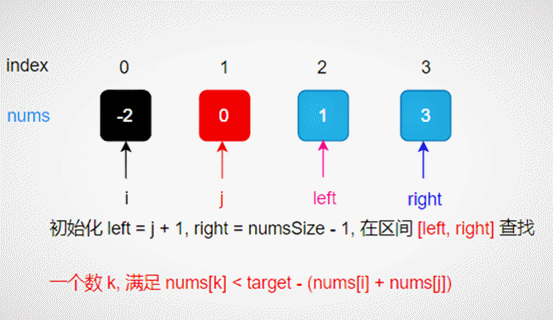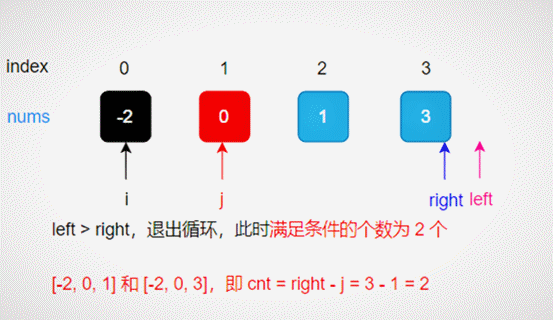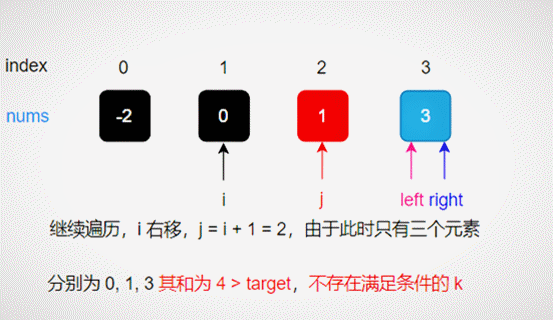
First fix i and j, and then find k satisfying the condition in (J, numsize - 1];
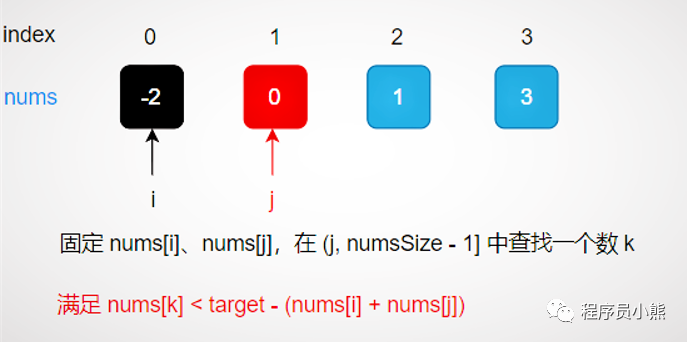
Determine search interval
Shorten the search interval according to the size relationship between num [mid] and target - num [i] - num [J];
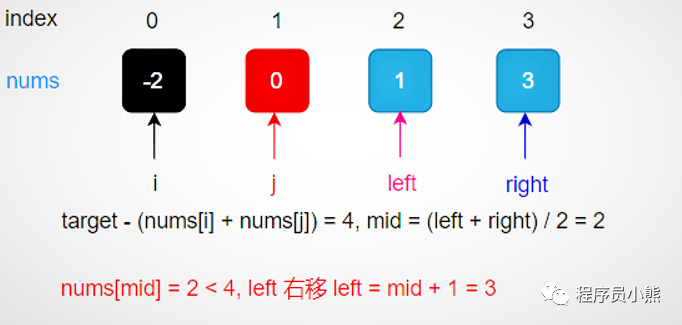
Narrow the search
Then determine the logarithm of the triples that meet the conditions.
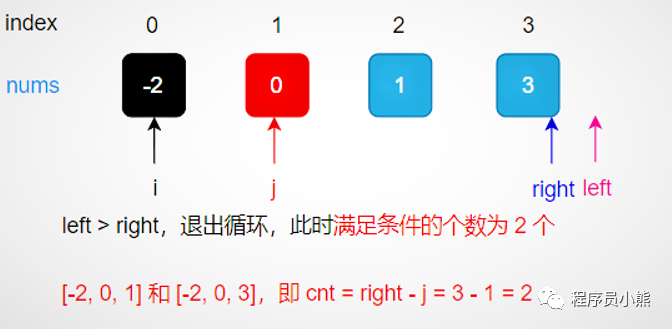
Determine the logarithm of the appropriate triples
The sorting + binary search method is adopted to complete the search process, as shown in the following figure:
Search process (sort + dichotomy)
Show me the Code
C
int comp(const void *a, const void *b) {
return *(int *)a - *(int *)b;
}
int threeSumSmaller(int* nums, int numsSize, int target){
if (nums == NULL || numsSize < 3) {
return 0;
}
int cnt = 0;
qsort(nums, numsSize, sizeof(int), comp);
for (int i = 0; i < numsSize - 2; ++i) {
for (int j = i + 1; j < numsSize - 1; ++j) {
int sum = target - nums[i] - nums[j];
int left = j + 1, right = numsSize - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] >= sum) {
right = mid - 1;
} else {
left = mid + 1;
}
}
cnt += (right - j);
}
}
return cnt;
}
C++
int threeSumSmaller(vector<int>& nums, int target) {
int cnt = 0;
int size = nums.size();
sort(nums.begin(), nums.end());
for (int i = 0; i < size - 2; ++i) {
for (int j = i + 1; j < size - 1; ++j) {
int sum = target - nums[i] - nums[j];
int left = j + 1, right = size - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] >= sum) {
right = mid - 1;
} else {
left = mid + 1;
}
}
cnt += (right - j);
}
}
return cnt;
}
Java
int threeSumSmaller(int[] nums, int target) {
int cnt = 0;
Arrays.sort(nums);
int size = nums.length;
for (int i = 0; i < size - 2; ++i) {
for (int j = i + 1; j < size - 1; ++j) {
int sum = target - nums[i] - nums[j];
int left = j + 1, right = size - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] >= sum) {
right = mid - 1;
} else {
left = mid + 1;
}
}
cnt += (right - j);
}
}
return cnt;
}
Python3
def threeSumSmaller(nums, target):
nums.sort()
cnt, size = 0, len(nums)
for i in range(len(nums) - 2):
for j in range(i + 1, size - 1):
sum = target - nums[i] - nums[j]
left, right = j + 1, size - 1
while left <= right:
mid = (right + left) // 2
if nums[mid] >= sum:
right = mid - 1
else:
left = mid + 1
cnt += (right - j)
return cnt
Golang
func threeSumSmaller(nums []int, target int) int {
if len(nums) < 3 {
return 0
}
cnt := 0
sort.Ints(nums)
for i := 0; i < len(nums) - 2; i++ {
for j := i + 1; j < len(nums) - 1; j++ {
sum := target - nums[i] - nums[j]
left, right := j + 1, len(nums) - 1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] >= sum {
right = mid - 1
} else {
left = mid + 1
}
}
cnt = cnt + right - j
}
}
return cnt
}
Complexity analysis
Time complexity: O(n^2lgn), where n is the length of the array.
Space complexity: O(1), no additional storage space is opened up.
Solution 3: sorting + collision pointer
In case of search related problems, if they are still orderly, in addition to binary search, the collision pointer method in double pointers can also be used to solve them.
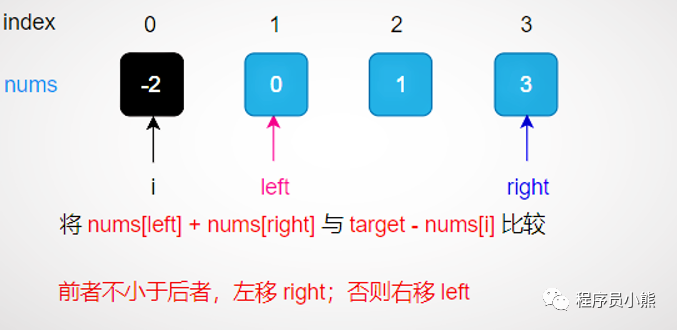
give an example
Take num = [- 2,0,1,3], target = 2 as an example, as shown in the figure below.

Example
Compare the size relationship between num [left] + num [right] and target - num [i], so as to narrow the search range;
Search method
Determines the logarithm of the triples that satisfy the condition.
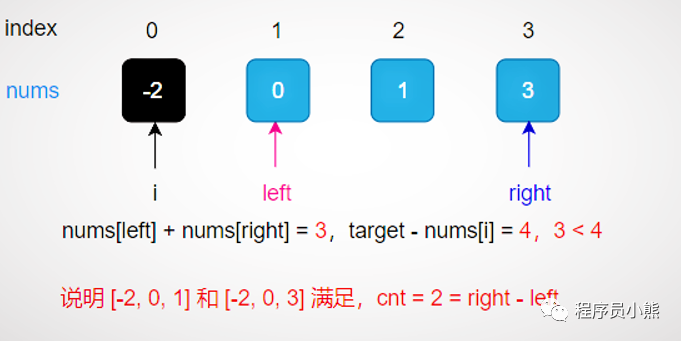
Determine results
The sorting + collision pointer method is used to complete the search process, as shown in the following figure:
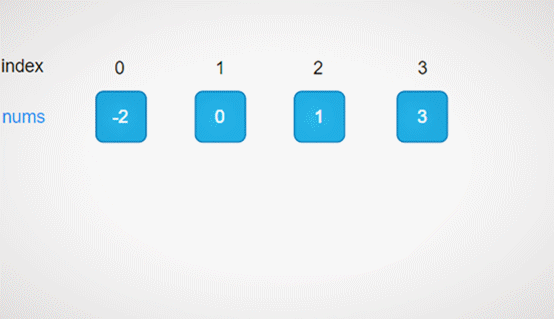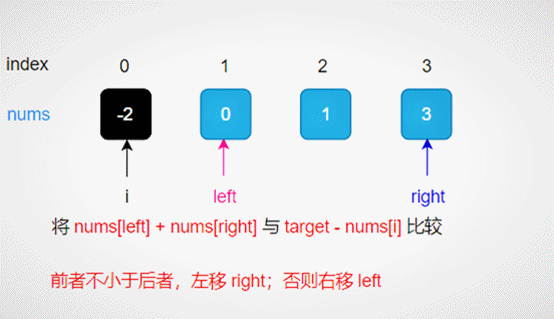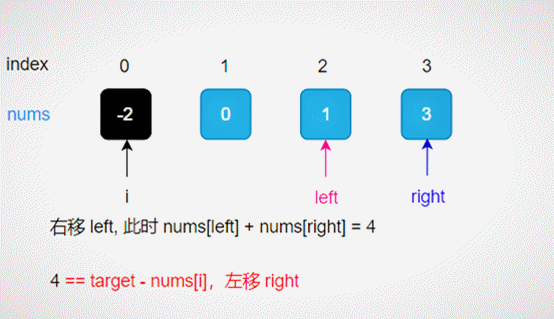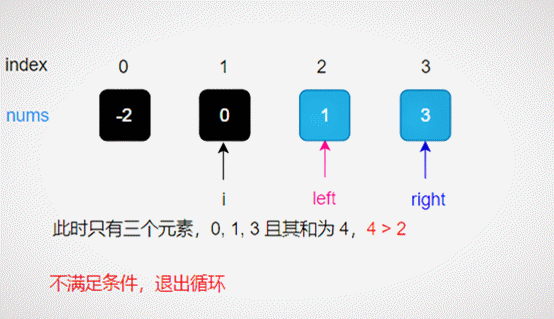
Sorting + collision fingerpin search process
Show me the Code
C
int comp(const void *a, const void *b) {
return *(int *)a - *(int *)b;
}
int threeSumSmaller(int* nums, int numsSize, int target){
if (nums == NULL || numsSize < 3) {
return 0;
}
int cnt = 0;
qsort(nums, numsSize, sizeof(int), comp);
for (int i = 0; i < numsSize - 2; i++) {
int sum = target - nums[i];
int left = i + 1, right = numsSize - 1;
while (left < right) {
if (nums[left] + nums[right] < sum) {
cnt += (right - left);
left++;
} else {
right--;
}
}
}
return cnt;
}
C++
int threeSumSmaller(vector<int>& nums, int target) {
int cnt = 0;
int size = nums.size();
sort(nums.begin(), nums.end());
for (int i = 0; i < size - 2; ++i) {
int sum = target - nums[i];
int left = i + 1, right = size - 1;
while (left < right) {
if (nums[left] + nums[right] < sum) {
cnt += (right - left);
left++;
} else {
right--;
}
}
}
return cnt;
}
Java
int threeSumSmaller(int[] nums, int target) {
int cnt = 0;
Arrays.sort(nums);
int size = nums.length;
for (int i = 0; i < size - 2; ++i) {
int sum = target - nums[i];
int left = i + 1, right = size - 1;
while (left < right) {
if (nums[left] + nums[right] < sum) {
cnt += (right - left);
left++;
} else {
right--;
}
}
}
return cnt;
}
Python3
def threeSumSmaller(nums, target):
nums.sort()
cnt, size = 0, len(nums)
for i in range(len(nums) - 2):
sum = target - nums[i]
left, right = i + 1, size - 1;
while left < right:
if nums[left] + nums[right] < sum:
cnt += (right - left)
left += 1
else:
right -= 1
return cnt
Golang
func threeSumSmaller(nums []int, target int) int {
if len(nums) < 3 {
return 0
}
cnt := 0
sort.Ints(nums)
for i := 0; i < len(nums) - 2; i++ {
sum := target - nums[i]
left, right := i + 1, len(nums) - 1
for left < right {
if nums[left] + nums[right] < sum {
cnt += (right - left)
left += 1
} else {
right -= 1
}
}
}
return cnt
}
Complexity analysis
Time complexity: O(n^2), where n is the length of the array.
Space complexity: O(1), no additional storage space is opened up.