Feeling like National Day is busier than working, I finally got free and didn't write code for five days for fear of being handy. I just got bored and wrote a Gerstner calculation by the way.
Gerstner is a pseudo-real algorithm used in earlier graphics algorithms to simulate water surface waves. It is based on a combination of sine and cosine waves, which are explained in detail. First, officially:
trochoidal_wave
wind_wave
wave
What exactly is an overlay? First, let's write the effect of a sinusoidal wave:
Grid building:

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

[ExecuteInEditMode]
[RequireComponent(typeof(MeshRenderer))]
[RequireComponent(typeof(MeshFilter))]
public class WaveRectanglePanel : MonoBehaviour
{
    public int horizonCount = 50;
    public int verticalCount = 50;

    [Range(0.1f, 100f)]
    public float cellDistance = 1f;

    public bool isUpdate = false;

    private MeshRenderer meshRender;
    private MeshFilter meshFilter;

    private Mesh mesh;

    void Start()
    {
        meshRender = GetComponent<MeshRenderer>();
        meshFilter = GetComponent<MeshFilter>();
        mesh = new Mesh();
    }

    void Update()
    {
        if (isUpdate)
        {
            UpdateMesh();
            isUpdate = false;
        }
    }

    private void UpdateMesh()
    {
        if (mesh != null)
        {
            mesh.Clear();
        }
        Vector3[] vertices = new Vector3[(horizonCount + 1) * (verticalCount + 1)];
        Vector3[] normals = new Vector3[(horizonCount + 1) * (verticalCount + 1)];
        Vector2[] uvs = new Vector2[(horizonCount + 1) * (verticalCount + 1)];
        int[] triangles = new int[horizonCount * verticalCount * 6];
        int triindex = 0;
        for (int y = 0; y <= verticalCount; y++)
        {
            for (int x = 0; x <= horizonCount; x++)
            {
                int index = (horizonCount + 1) * y + x;
                vertices[index] = new Vector3(x * cellDistance, 0, -y * cellDistance);
                normals[index] = new Vector3(0, 1, 0);
                uvs[index] = new Vector2((float)x / (float)horizonCount, (float)y / (float)verticalCount);
                if (x < horizonCount && y < verticalCount)
                {
                    int topindex = x + y * (horizonCount + 1);
                    int bottomindex = x + (y + 1) * (horizonCount + 1);
                    triangles[triindex] = topindex;
                    triangles[triindex + 1] = topindex + 1;
                    triangles[triindex + 2] = bottomindex + 1;
                    triangles[triindex + 3] = topindex;
                    triangles[triindex + 4] = bottomindex + 1;
                    triangles[triindex + 5] = bottomindex;
                    triindex += 6;
                }
            }
        }
        mesh.vertices = vertices;
        mesh.normals = normals;
        mesh.triangles = triangles;
        mesh.uv = uvs;

        meshFilter.sharedMesh = mesh;
    }
}

* Next implement the sin wave effect

Shader "GerstnerWave/SinWaveShader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _WaveSpeed("Wave Speed",Range(0.1,10)) = 1 
        _WavePower("Wave Power",Range(0.1,10)) = 1
        _WaveRange("Wave Range",Range(0.1,10)) = 1
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            float _WaveSpeed;
            float _WavePower;
            float _WaveRange;

            v2f vert (appdata v)
            {
                v2f o;
                //sin-in factor on x or z axis to control wave
                float s = sin(v.vertex.x*_WavePower+_Time.y*_WaveSpeed)*_WaveRange;
                v.vertex += float4(0,s,0,0);
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = tex2D(_MainTex, i.uv);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:

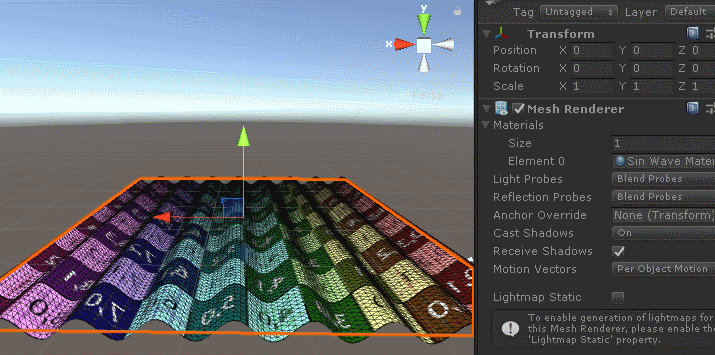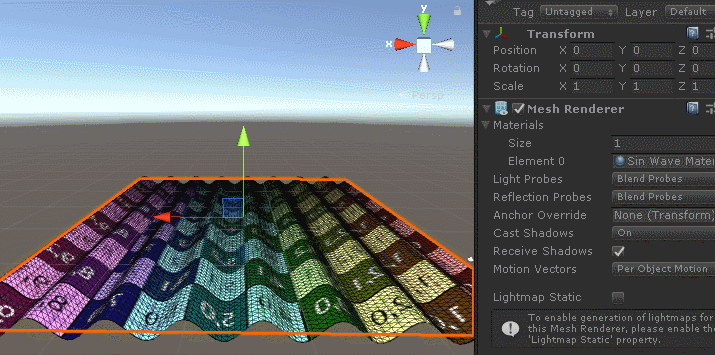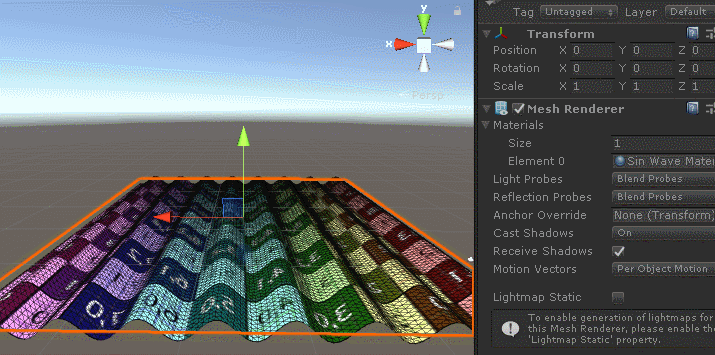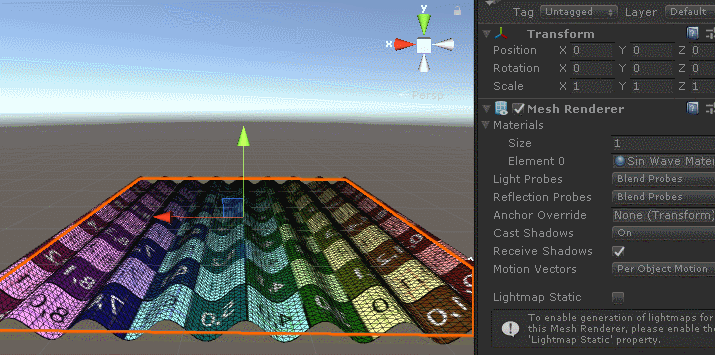
First, we create a horizontal planar grid with a y-axis of 0, so the effect of waves can be obtained by sinusoidal wave incorporation calculations using x and y values at the vertices of the grid in the shader.
In reality, however, the wave peaks are obviously sharp rather than smooth, as shown in the following figure:

Official Mathematical Schematics:
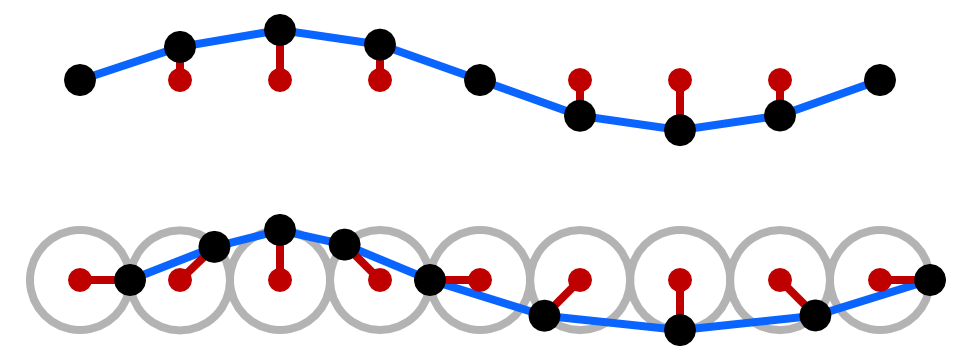ps: sin s at the top and gerstner at the bottom.
At the same time, we can see that gerstner sampling is cos sampling with an X (or z) axis superimposed (or subtracted) on the basis of sin sampling. We can think about it in our mind that by comparing the black origin of the upper and lower graphs, we can see that the origin does not change on the y axis, but has a periodic change on the X (or z) axis (sin x = cos (90-x))

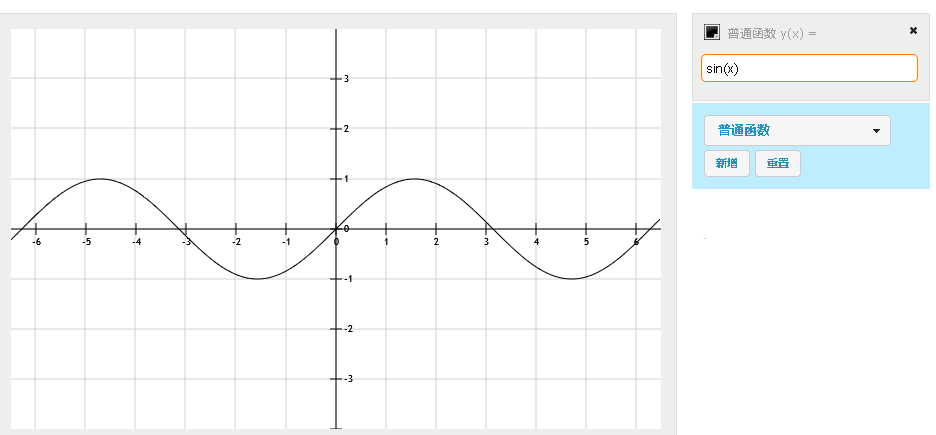
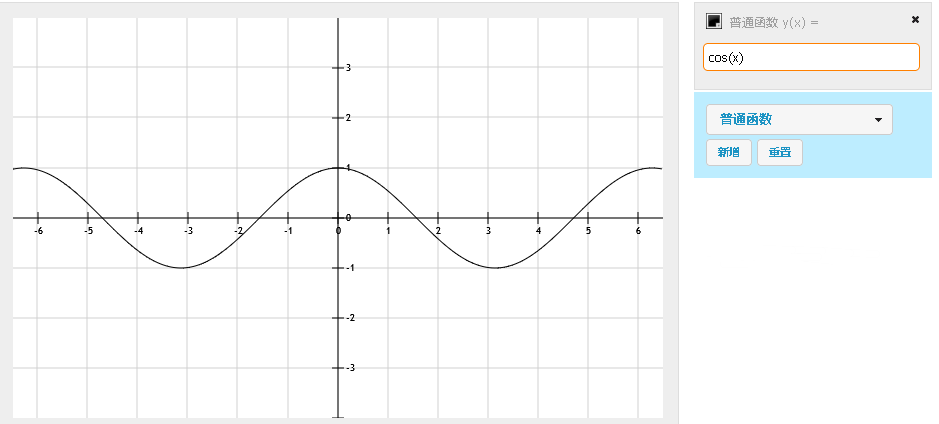
Then, in order to verify our ideas, it's easy to see that.

Shader "GerstnerWave/GerstnerWaveShader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _WaveRadius("Wave Circle Radius",Range(0.1,10)) = 1
        _WaveSpeed("Wave Speed",Range(0.1,10)) = 1
        _WaveRange("Wave Range",Range(0.1,10)) = 1
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            float _WaveRadius;
            float _WaveSpeed;
            float _WaveRange;

            v2f vert (appdata v)
            {
                v2f o;
                //angle Involvement
                float ang = v.vertex.x + _WaveSpeed*_Time.y;
                //y-axis sin overlay
                float y = _WaveRange*sin(ang)*_WaveRadius;
                //x-axis cos reduction
                float x = _WaveRange*cos(ang)*_WaveRadius;
                v.vertex += float4(x,y,0,0);
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = tex2D(_MainTex, i.uv);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:
You can see that such a water wave is more real. Of course, the water wave is not a fixed X or z axis direction, so if we could add a two-dimensional (x z axis) direction, it would be better as follows:

(It can be seen that at this time the peaks move along the X and z axes due to the direction (dir), so we can imagine that the larger the point product of the X oz plane vertex with dir (i.e., the smaller the angle between x'oz'and dir)The closer this vertex approaches the peak, the larger the input parameter involved in the sine-cosine calculation, and the components of the X and z fluctuations moving vertically also need to be calculated according to the components of dir, X and y.

Shader "GerstnerWave/GerstnerWaveDirectionShader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _WaveDirection("Wave Direction",vector) = (1,0,0,0)
        _WaveRadius("Wave Circle Radius",Range(0.1,10)) = 1
        _WaveSpeed("Wave Speed",Range(0.1,10)) = 1
        _WaveRange("Wave Range",Range(0.1,10)) = 1
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            float2 _WaveDirection;
            float _WaveRadius;
            float _WaveSpeed;
            float _WaveRange;

            v2f vert (appdata v)
            {
                v2f o;
                //Direct input of the unit vector is better
                float2 dir = normalize(_WaveDirection);
                //dot(dir,v.vertex.xz) obtains the point product (weight) of the XZ two-dimensional vector and the dir vector in vertex modeling space
                //Peak weights used to determine vertex (i.e. sine-cosine function parameters)
                float ang = dot(dir,v.vertex.xz) + _WaveSpeed*_Time.y;
                //x-direction overlay and z-direction overlay need to be calculated based on dir components
                float x = dir.x*_WaveRange*cos(ang)*_WaveRadius;
                float y = _WaveRange*sin(ang)*_WaveRadius;
                float z = dir.y*_WaveRange*cos(ang)*_WaveRadius;
                v.vertex += float4(x,y,z,0);
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = tex2D(_MainTex, i.uv);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:

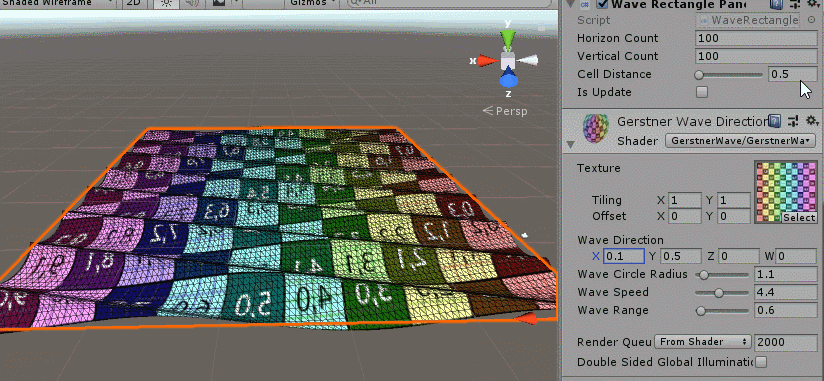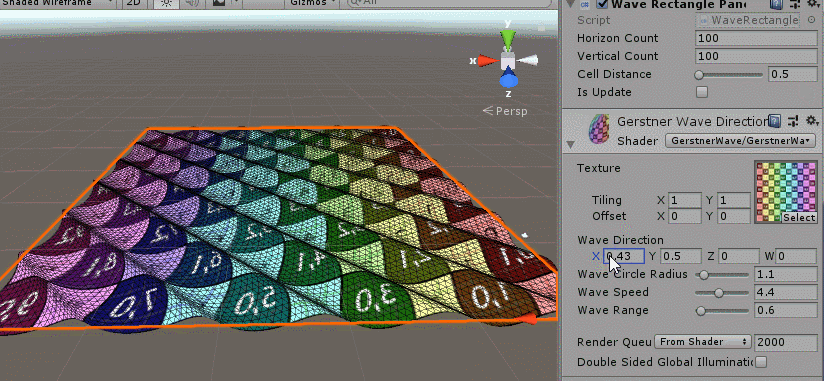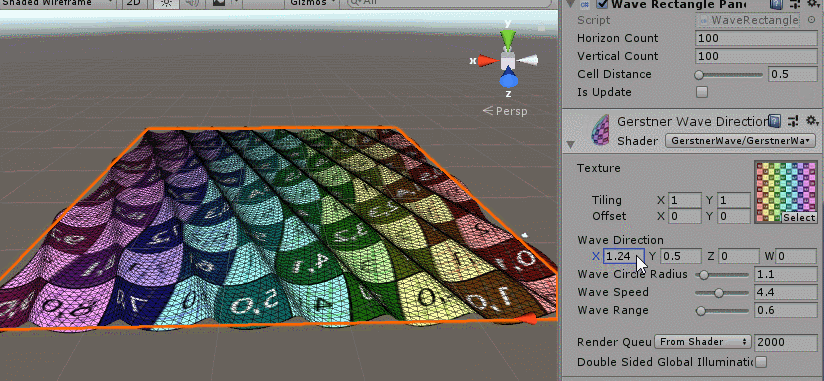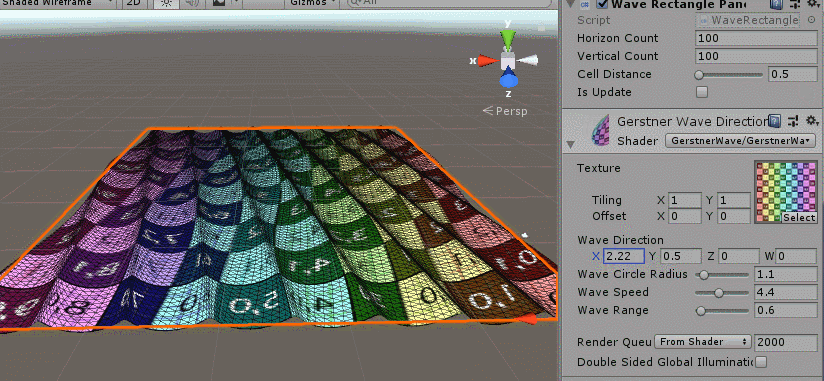
You can see that the effect is achieved. Next, we have to do a multiwave overlay. The water surface is really the result of many waves.

Shader "GerstnerWave/GerstnerMultiWaveShader"
{
     Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _WaveDir1("Wave Direction 1",vector) = (1,0,0,0)
        _WaveDir2("Wave Direction 2",vector) = (1,0,0,0)
        _WaveDir3("Wave Direction 3",vector) = (1,0,0,0)
        _WaveRadius("Wave Circle Radius",Range(0.1,10)) = 1
        _WaveSpeed("Wave Speed",Range(0.1,10)) = 1
        _WaveRange("Wave Range",Range(0.1,10)) = 1
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            float2 _WaveDir1;
            float2 _WaveDir2;
            float2 _WaveDir3;
            float _WaveRadius;
            float _WaveSpeed;
            float _WaveRange;

            float4 getGerstnerWave(float4 vtx,float2 dir,float wavespd,float waverag,float waverad)
            {
                float ang = dot(dir,vtx.xz) + wavespd*_Time.y;
                float x = dir.x*waverag*cos(ang)*waverad;
                float y = waverag*sin(ang)*waverad;
                float z = dir.y*waverag*cos(ang)*waverad;
                return float4(x,y,z,0);
            }

            v2f vert (appdata v)
            {
                v2f o;
                float2 dir1 = normalize(_WaveDir1);
                float4 vtx1 = getGerstnerWave(v.vertex,dir1,_WaveSpeed,_WaveRange,_WaveRadius);
                float2 dir2 = normalize(_WaveDir2);
                float4 vtx2 = getGerstnerWave(v.vertex,dir2,_WaveSpeed,_WaveRange,_WaveRadius);
                float2 dir3 = normalize(_WaveDir3);
                float4 vtx3 = getGerstnerWave(v.vertex,dir3,_WaveSpeed,_WaveRange,_WaveRadius);
                v.vertex += (vtx1+vtx2+vtx3);
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = tex2D(_MainTex, i.uv);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:

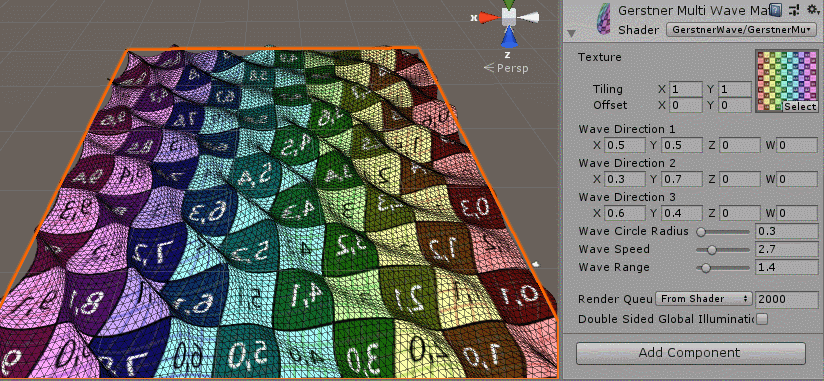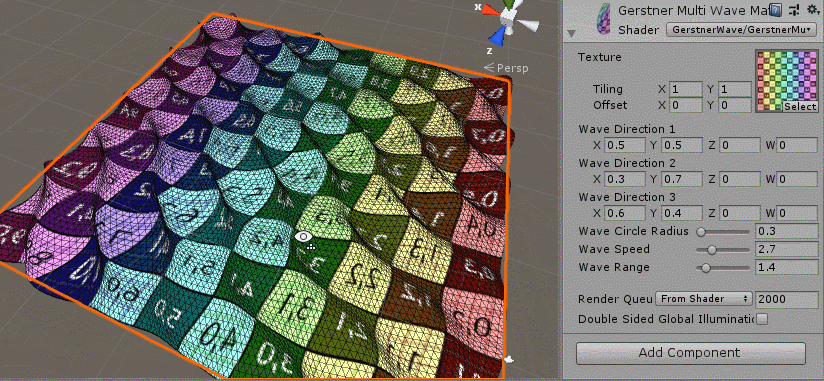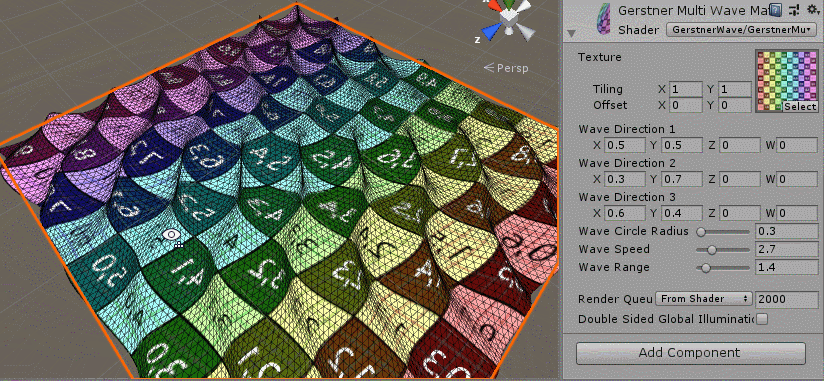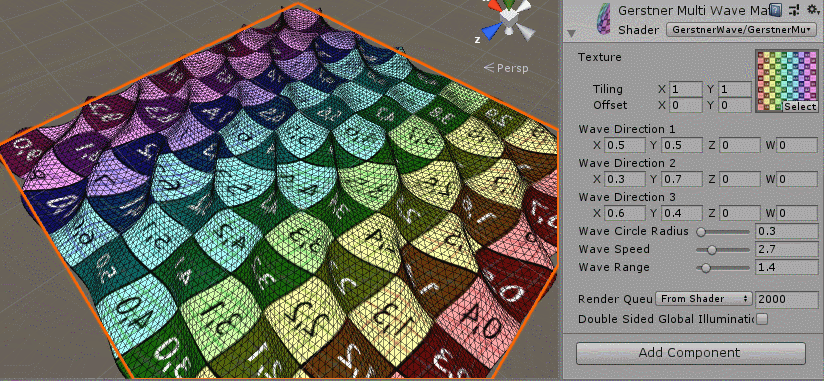
You can see that the multiwave overlay function has been implemented, but what you always feel is that it is random, because we have to modify the settings for the added parameters since we have three random direction s and all the other parameters are the same.

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class GerstnerMultiRandomWave : MonoBehaviour
{
    [System.Serializable]
    public class WaveParams
    {
        public float WaveDirX;
        public float WaveDirY;
        public float WaveRadius;
        public float WaveSpeed;
        public float WaveRange;
    }

    public Material waveMat;

    public bool updateParam = false;

    public WaveParams[] waveParams;

    void Start()
    {

    }

    private void Update()
    {
        if (updateParam)
        {
            UpdateWaveParam();
            updateParam = false;
        }
    }

    private void UpdateWaveParam()
    {
        int count = waveParams.Length;
        waveMat.SetInt("_WaveCount", count);
        waveMat.SetFloatArray("_WaveParams", GetWaveParamFloats());
    }

    private List<float> GetWaveParamFloats()
    {
        List<float> floatlist = new List<float>();
        for (int i = 0; i < waveParams.Length; i++)
        {
            WaveParams param = waveParams[i];
            floatlist.Add(param.WaveDirX);
            floatlist.Add(param.WaveDirY);
            floatlist.Add(param.WaveRadius);
            floatlist.Add(param.WaveSpeed);
            floatlist.Add(param.WaveRange);
        }
        return floatlist;
    }
}

shader modification:

Shader "GerstnerWave/GerstnerMultiParamWaveShader"
{
     Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            const int _WaveCount;
            float _WaveParams[30];          //Up to 6

            float4 getGerstnerWave(float4 vtx,float2 dir,float wavespd,float waverag,float waverad)
            {
                float ang = dot(dir,vtx.xz) + wavespd*_Time.y;
                float x = dir.x*waverag*cos(ang)*waverad;
                float y = waverag*sin(ang)*waverad;
                float z = dir.y*waverag*cos(ang)*waverad;
                return float4(x,y,z,0);
            }

            v2f vert (appdata v)
            {
                v2f o;
                for(int i=0;i<_WaveCount;i++)
                {
                    int index = i*5;
                    float2 dir = float2(_WaveParams[index],_WaveParams[index+1]);
                    float spd = _WaveParams[index+2];
                    float rag = _WaveParams[index+3];
                    float rad = _WaveParams[index+4];
                    float4 wvtx = getGerstnerWave(v.vertex,dir,spd,rag,rad);
                    v.vertex += wvtx;
                }
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = tex2D(_MainTex, i.uv);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:

The only way to get good results is to adjust the parameters, so I can just adjust a few values.
You haven't finished yet. Next we have to deal with the problem of coloring, which is the recalculation of normal vectors. If we don't recalculate normal vectors, this will be the case:

I added the specular component calculation and found that the specular highlight is also a board. If we increase the recalculation of the normal vector, the specular highlight will be displayed properly.
How can we recalculate? Our original vertex normal vector is (0,1,0), and then vertex fluctuates (moves) along the three axes of xyz as follows:

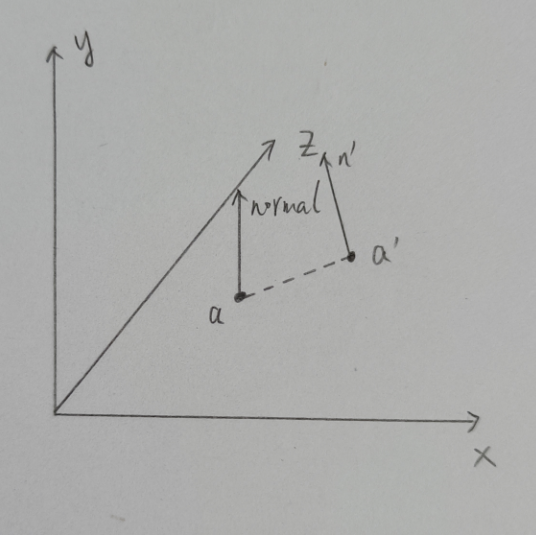
In this case, the new normal n'is simply calculated by the cross product of tangents and subtracts, since tangents and subtracts are still good, as follows:

(2) We can understand that affine coordinate system t b n (tangent, bitangent, normal) has reached t'b'n'b y rotating and translating, but we don't need to calculate the translation here, just consider the rotation. So we get tangent, bitangent rotation around the y-axis through z, plus (0, y, 0)Vectors get tangent', bitangent', and normal'is obtained by cross-product.
Of course, there is no need to rotate the matrix, and direct vector calculation is also possible.
Naturally, if our fluctuations take into account the angle used, then the rotation of the matrix is better.
The following is an example of "a fluctuation" to illustrate the process of tangent and bitangent transforming to t', bt'after each "fluctuation":

Imagine tangent and bitangent transformed to t1 and bt1 by rotation on the xz plane, and then in xyz three-dimensional space, t', bt', are obtained by adding (0,y,0). Here's a test:

Shader "GerstnerWave/GerstnerMultiParamWaveShader"
{
    Properties
    {
        _MainColor("Main Color",Color) = (1,1,1,1)
        _MainTex ("Texture", 2D) = "white" {}
        [Toggle]_IsCalNorm("Calculate Normal?",int) = 0
        _LightFactor("Lighting Factor",Color) = (1,1,1,1)
        _DiffuseFactor("Diffuse Factor",Color) = (1,1,1,1)
        _SpecFactor("Specular Factor",Color) = (1,1,1,1)
        _SpecGloss("Specular Gloss",Range(0,500)) = 20
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"
            #include "Lighting.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
                float4 normal : NORMAL;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
                float3 wdNorm : TEXCOORD1;
                float3 wdP2S : TEXCOORD2; 
                float3 wdP2V : TEXCOORD3;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;

            float4 _MainColor;

            int _IsCalNorm;

            float4 _LightFactor;
            float4 _DiffuseFactor;
            float4 _SpecFactor;
            float _SpecGloss;
            
            const int _WaveCount;
            float _WaveParams[30];          //Up to 6

            float4 getGerstnerWave(float4 vtx,float2 dir,float wavespd,float waverag,float waverad,inout float3 tang,inout float3 bitang)
            {
                float ang = dot(dir,vtx.xz) + wavespd*_Time.y;
                float x = dir.x*waverag*cos(ang)*waverad;
                float y = waverag*sin(ang)*waverad;
                float z = dir.y*waverag*cos(ang)*waverad;
                float3 t1 = normalize(tang+float3(0,0,z));
                tang = normalize(t1+float3(0,y,0));
                float3 bt1 = normalize(bitang+float3(z,0,0));
                bitang = normalize(bt1+float3(0,y,0));
                return float4(x,y,z,0);
            }

            v2f vert (appdata v)
            {
                v2f o;
                //Original tangent, bitangent
                float3 otan = float3(1,0,0);            
                float3 obitan = float3(0,0,1);
                for(int i=0;i<_WaveCount;i++)
                {
                    int index = i*5;
                    float2 dir = float2(_WaveParams[index],_WaveParams[index+1]);
                    float spd = _WaveParams[index+2];
                    float rag = _WaveParams[index+3];
                    float rad = _WaveParams[index+4];
                    float4 wvtx = getGerstnerWave(v.vertex,dir,spd,rag,rad,otan,obitan);
                    v.vertex += wvtx;
                }
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                if(_IsCalNorm){
                    //Calculate world space normal
                    o.wdNorm = UnityObjectToClipPos(cross(otan,obitan));
                }else{
                    o.wdNorm = UnityObjectToClipPos(v.normal);
                }
                o.wdP2S = WorldSpaceLightDir(v.vertex);
                o.wdP2V = WorldSpaceViewDir(v.vertex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                fixed4 col = _MainColor;
                float3 wdnorm = normalize(i.wdNorm);
                float3 wdp2s = normalize(i.wdP2S);
                float3 wdp2v = normalize(i.wdP2V);
                float3 hdir =  normalize(wdp2s+wdp2v);
                float ndotl = dot(wdnorm,wdp2s);
                float ndoth = dot(wdnorm,hdir);

                //Calculate illumination
                fixed4 light = _LightColor0*_LightFactor;

                float diff = max(0,ndotl);
                fixed4 diffcol = diff*_LightColor0*_DiffuseFactor;
                
                float spec = pow(max(0,ndoth),_SpecGloss);
                fixed4 speccol = spec*_LightColor0*_SpecFactor;

                col*=(light+diffcol+speccol);
                return col;
            }
            ENDCG
        }
    }
}

The effect is as follows:

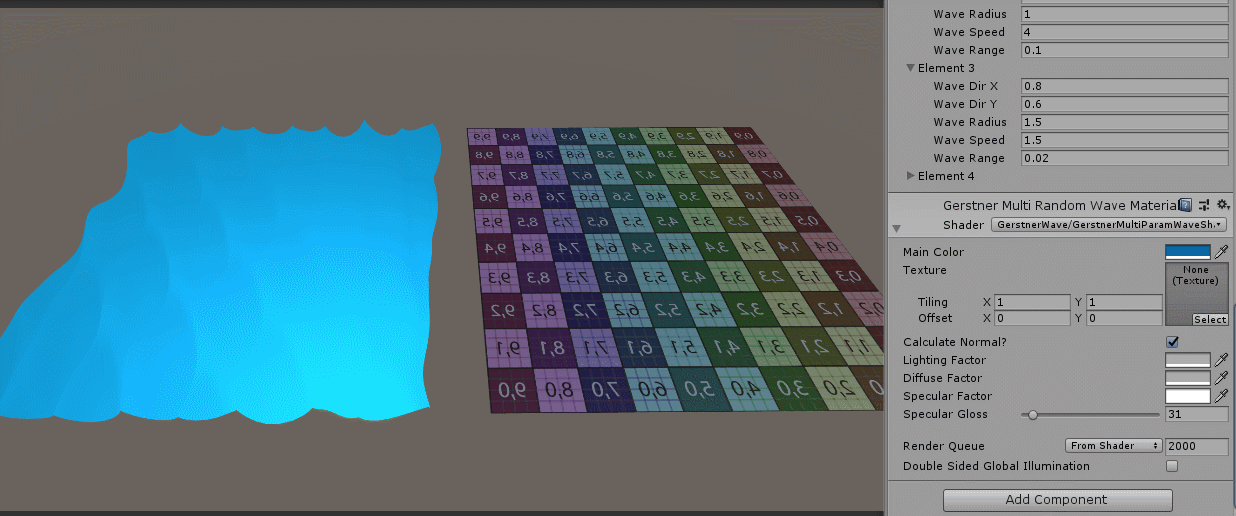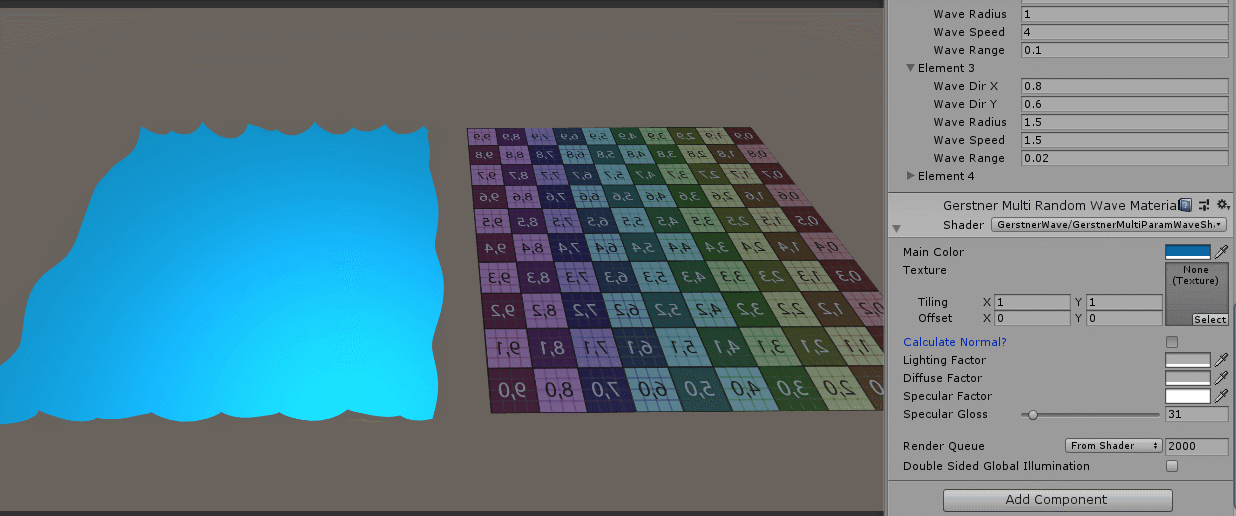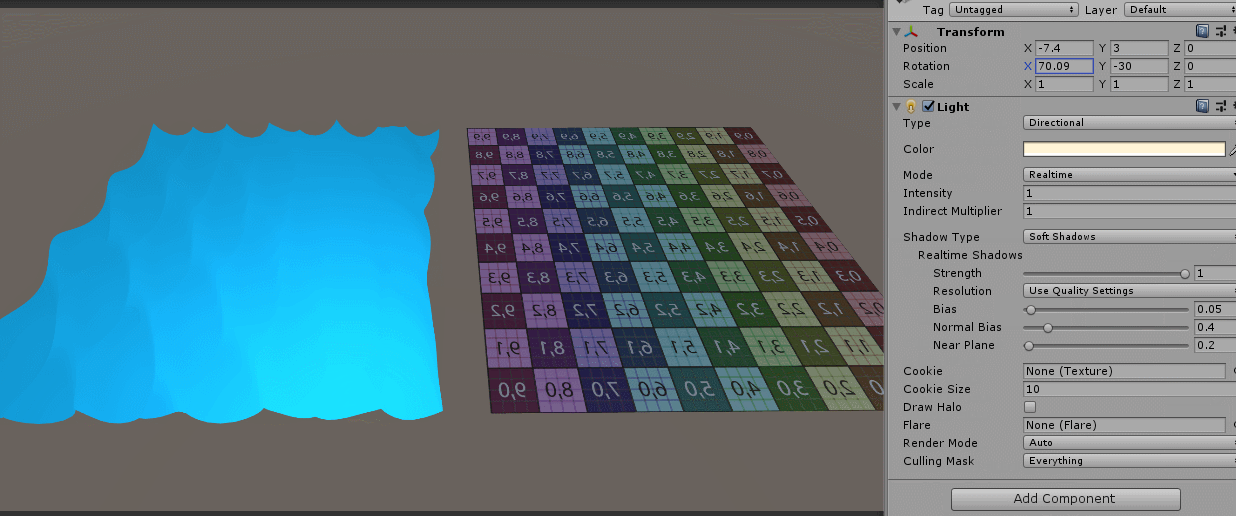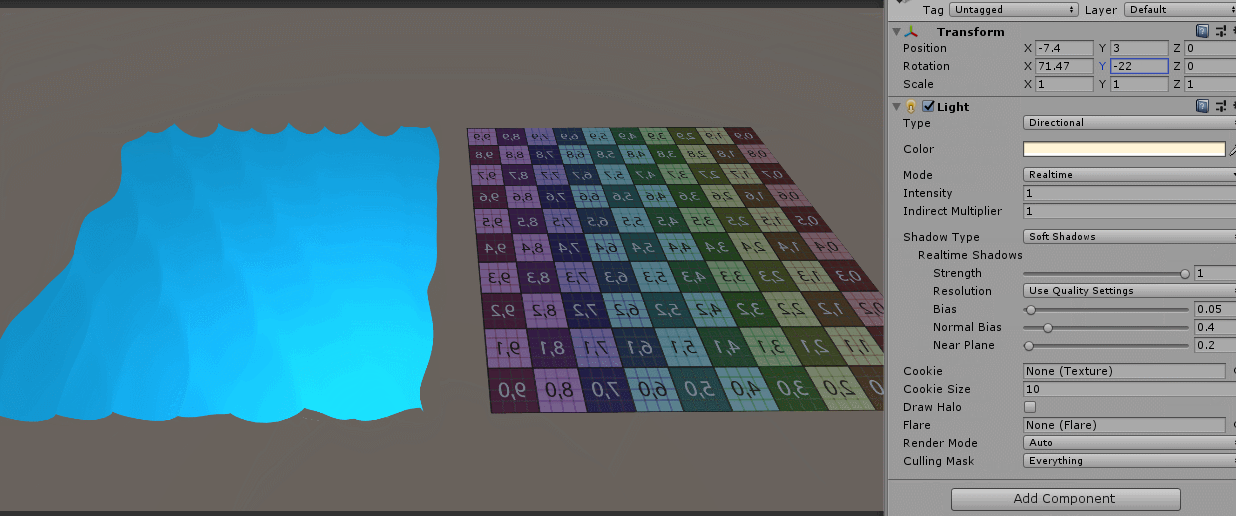
You can see that the problem is not serious, and the normal vector seems to be right. Okay, there's time to continue later. Talk about what I've written about an interactive water body.