Introduction to GA Theory

Genetic Algorithm s (GA) is a computational model to simulate the natural selection and genetic mechanism of Darwin's biological evolution theory. It is a method to search the optimal solution by simulating the natural evolution process. (Baidu Explanation)

The core of genetic algorithm is natural selection. Natural selection is to eliminate species that are unsuitable for survival and remain environmentally adaptable.

It's like having a group of very mysterious species (some individuals are very ordinary, can't fly, some individuals are born with a small wing, some individuals are born with a big wing), but they all have a common preference, that is, they like to take risks, they like to jump to cliffs. At this time, the survival rate of non-flying individuals is quite low, many of them died, the survival rate of individuals with small wings is higher, only a few died, of course, individuals with large wings, only a few died. At this time, the surviving individuals return to the cliff again, reproduce their offspring, inherit the genes of their predecessors, or some will mutate. Then the group continued to jump up the cliff and circle, and eventually it could all survive after hundreds of generations. Ultimately adapt to the environment.

Genetic algorithm is to find the global optimal solution by iteration.

When using gradient descent to solve the problem, only the global optimal solution of U-shaped function can be found, but once a function similar to the following figure appears, gradient descent can only find the local optimal solution.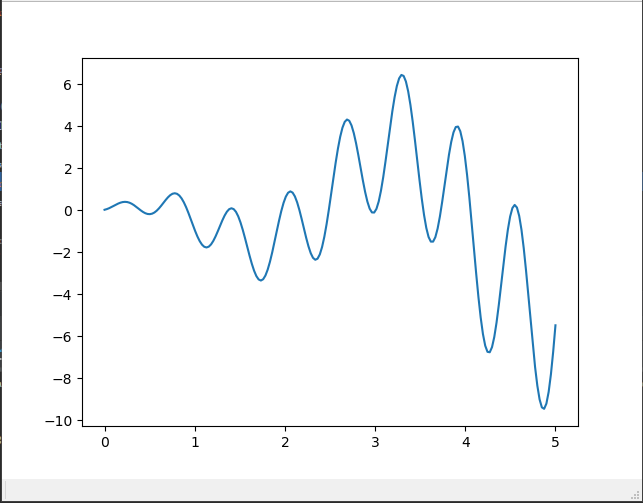

Therefore, it is necessary to find the global optimal solution by genetic algorithm.
Now generate a function graph with a hundred individuals randomly placed on it, as shown in Figure 1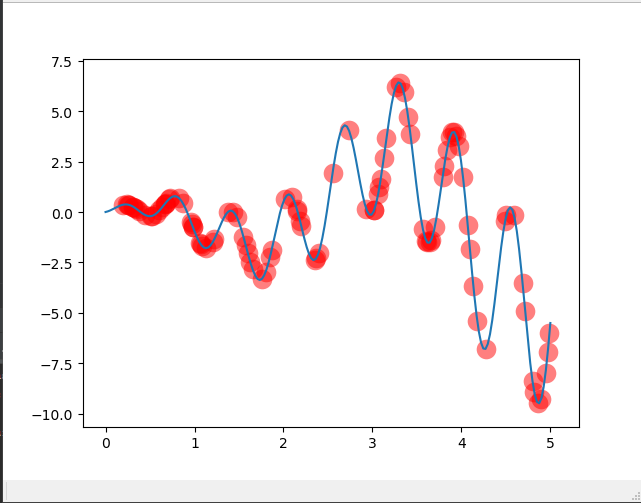

Let function value be expressed as fitness of each individual in the whole environment. That is to say, the higher fitness is, the stronger adaptability is. Now the aim is to cultivate a group of individuals with strong adaptability. So good parents are needed to mate to produce better offspring.
If there are only four groups in the population, fitness is 1, 2, 3 and 4, respectively, it is obvious that the higher the score, the better the genes are, the more mating they need. How to achieve multiple mating requires probability control. When fitness is added up to 1 + 2 + 3 + 4 = 10, the probability of each number is 0.1, 0.2, 0.3, 0.4. Now I will randomly generate the number according to this probability, so the probability of mating with No. 4 is high.
After mating, the genes of the offspring will have pits to mutate.
Then follow the steps above and iterate over and over again to produce excellent groups.

import numpy as np
import matplotlib.pyplot as plt

DNA_SIZE = 10            # The length of DNA is expressed in [01010101], and mating is the exchange of some genes (the most x-axis input).
POP_SIZE = 100           # population size
CROSS_RATE = 0.8         # The individual has a 0.8 chance of finding a mate for mating.
MUTATION_RATE = 0.003    # Probability of Gene Mutation by mutation probability
N_GENERATIONS = 200#Number of iterations
X_BOUND = [0, 5]         # Range of values of x-upper and lower bounds X-axis

Define the function that needs to find the optimal solution, which is the graph above.

def F(x): return np.sin(10*x)*x + np.cos(2*x)*x     # to find the maximum of this function

find non-zero fitness for selection

The size of the value of the function obtained is fitness. Why return this form? The purpose is to ensure that there is no negative number when calculating the probability. 1e-3 is to ensure that the probability does not return to zero, so that the probability is not zero.

def get_fitness(pred): return pred + 1e-3 - np.min(pred)

convert binary DNA to decimal and normalize it to a range(0, 5)

Genes are binary, converted to decimal, and controlled between 0 and 5.

def translateDNA(pop): return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1] 

Selection of mating population based on probability

def select(pop, fitness):    # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=fitness/fitness.sum())
    return pop[idx]

If the probability of 0.8 is to obtain the right of mating, it is necessary to exchange genes and generate new individuals.

def crossover(parent, pop):     # mating process (genes crossover)
    if np.random.rand() < CROSS_RATE:
        i_ = np.random.randint(0, POP_SIZE, size=1)                             # select another individual from pop
        cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool)   # choose crossover points
        parent[cross_points] = pop[i_, cross_points]                            # mating and produce one child
    return parent

Gene mutation, the probability of 0.003 mutations per gene 0 to 1, 1 to 0

def mutate(child):
    for point in range(DNA_SIZE):
        if np.random.rand() < MUTATION_RATE:
            child[point] = 1 if child[point] == 0 else 0
    return child

Generating Groups

pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))   # initialize the pop DNA

Draw the most primitive picture

plt.ion()       # something about plotting
x = np.linspace(*X_BOUND, 200)
plt.plot(x, F(x))

Iteration generates many generations

for _ in range(N_GENERATIONS):
    F_values = F(translateDNA(pop))    # compute function value by extracting DNA

    # something about plotting
    if 'sca' in globals(): sca.remove()
    sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5); plt.pause(0.05)

    # GA part (evolution)
    fitness = get_fitness(F_values)
    print("Most fitted DNA: ", pop[np.argmax(fitness), :])
    pop = select(pop, fitness)
    pop_copy = pop.copy()
    for parent in pop:
        child = crossover(parent, pop_copy)
        child = mutate(child)
        parent[:] = child       # parent is replaced by its child

plt.ioff(); plt.show()