Concepts of inheritance:

• Genetic algorithm is a computational model that simulates the natural selection and genetic mechanism of Darwin's biological evolution theory. It is a method to search for the best solution by simulating the natural evolution process.

The characteristics of genetic algorithms:

• Common features of search algorithms are
  • First, a set of candidate solutions is formed.
  • The applicability of these candidate solutions is calculated based on some usability conditions.
  • Some candidate solutions are retained according to fitness, while others are discarded.
  • Some operations are performed on the reserved candidate solution to form a new one.
• Because genetic algorithm is one of the search algorithms, it has the above characteristics. In addition, genetic algorithm has its own unique features:
  • The genetic algorithm starts with a bundle of solutions (multiple candidate solutions) rather than a single solution, which is the biggest difference from traditional optimization algorithms.
  • Genetic algorithm handles multiple individuals in a group at the same time, which facilitates parallel settlement
  • Genetic algorithm has basically different search space, which makes it more widely used.
  • The genetic algorithm does not use deterministic rules, but uses probability transition rules to guide its search direction.

Terminology in genetic algorithms

• Chromosomes: Chromosomes are genotypic individuals. A certain number of individuals make up a population. The number in a population is called Population size.
• Genes: Genes are elements in a string. Genes are used to represent individual characteristics, such as a string S=1011. Four of these elements, 1, 0, 1, 1, are called genes. Their values are called alleles.
• Locus: A locus is the position of a gene in a string.
• Feature: The characteristic value of a gene is the same as the binary weight.
• Fitness: Individuals'fitness to the environment is called fitness, and fitness functions are used to quantify fitness.

Principles of genetic algorithms

• Genetic algorithm flowchart

• Selection: Selecting the winner and eliminating the inferior is called selection, which is based on the evaluation of individual fitness. The methods include roulette selection, random traversal sampling and local selection. For roulette selection, the probability of each individual being selected is proportional to the fitness, that is: p i = f i ∑ j = 1 n f i \color{blue}{p_i=\frac{f_i}{\sum_{j=1}^{n}f_i}} pi =j=1n fi. After calculating the individual selection probability, in order to mate an individual, multiple rounds of selection are needed, each of which produces a uniform random number between [0,1] the most selection pointer to determine the selected individual. Once selected, individuals can randomly form mating pairs.
• Crossing: The so-called crossover is the operation of replacing part of the structure of two parent individuals to produce a new individual. The crossover algorithm is
  • real valued recombination
  • Binary crossover
    The most common is the single intersection in binary intersection, which randomly calls parts of the structure before or after an intersection in two individual strings to produce two new individuals.
• Variation: Variation is the random selection of one or more loci according to the rate of variation and the reversal of these loci. The rate of variation is usually low, ranging from 0.001 to 0.1.
• Termination condition: When the fitness of the best individual reaches a given threshold, or when the fitness of the best individual and the fitness of the population do not rise, or when the number of iterations reaches a preset number, the algorithm terminates. Generally, the preset algebra is 100-500 generations.

• Selection of fitness function
  The fitness function should be designed to meet the following conditions
  • Single value, continuous, non-negative, maximize
  • Reasonable and consistent
  • Small computation
  • Strong versatility
• Selection of Initial Group
  The initial population is randomly generated.

Programming

For example, finding a function f ( x ) = 10 ∗ s i n ( 5 x ) + 7 ∗ c o s ( 4 x ) , x ∈ [ 0 , 10 ] \color{blue}{f(x)=10*sin(5x)+7*cos(4x),x\in[0,10]} f(x)=10_sin(5x)+7_cos(4x),x<[0,10]max

• Solution:
  • Initialization:

  function pop = initpop( popsize, chromlength )
      pop=round(rand(popsize,chromlength));
      %rand Random generation of 0 for each element~1 Decimals between, rows popsize,Number of columns chromlength Matrix of%
      %round Round each element of the matrix so that the result is 0 or 1%
  end
  

  • Target Function Value

  %Convert binary to decimal%
  function pop2 = decodebinary(pop )
      [rows,cols] = size(pop);%seek pop Number of rows and columns%
      for i=1:cols
             pop1(:,i)=2.^(cols-i).*pop(:,i);
      end
      pop2=sum(pop1,2);%seek pop1 Sum of each line%
  end
  

  %Its function is to convert chromosomal or binary encoding to decimal
  %Where parameters spoint Represents the starting position of a binary string with decoding
  %length Represents the length of the intercept
  function pop2= decodechrom(pop,spoint,length)
      pop1=pop(:,spoint:spoint+length-1);
      pop2=decodebinary(pop1);
  end
  

  %Its function is to calculate the value of the objective function
  function [objvalue] = calobjvalue(pop,length)
     temp=decodechrom(pop,1,length);%take pop Convert each row to a decimal number
     x=temp*10/(power(2,length)-1);%Converts the number in the binary field of each row to the number in the variable field
     objvalue=10*sin(5*x)+7*cos(4*x);%Calculate the value of the objective function
  end
  

• Fitness value

  %Calculate an individual's fitness
  function fitValue= calfitvalue( objValue)
      fitValue=objValue+100;%Design the fitness calculation function according to the situation
  end
  

• Cross operation

  %Crossover operation function
  function [ newpop] = crossover(pop,pc)
     [rows,cols]=size(pop);
     newpop=zeros(2*rows,cols);
     index=1;
     for i=1:rows
         other=i;
         if(rand<pc) %Each individual has the same probability of being selected to perform crossover   
             while other==i
                 other=1+floor(rand*rows);%Randomly select a crossover object
             end
             cpoint=floor(rand*cols)+1;%Randomly select an intersection
             %Execution Crossing
             newpop(i,:)=[pop(i,1:cpoint),pop(other,cpoint+1:cols)];
             newpop(rows+index,:)=[pop(other,1:cpoint),pop(i,cpoint+1:cols)];
             index=index+1;
         else
             newpop(i,:)=pop(i,:);
         end
     end
     newpop=newpop(1:rows+index-1,:);%Since the number of initialized rows is 2*rows，But the actual number of rows assigned is index-1 That's ok.
  end
  

• Variation operation

  %Variation operation
  function newpop = mutation( pop,pm)
      [rows,cols]=size(pop);
      newpop=ones(size(pop));
      for i=1:rows
          newpop(i,:)=pop(i,:);
          if rand<pm%If the random number is less than the mutation probability, select a mutation point to mutate this chromosome
              mpoint=round(rand*cols);%Random Selection of Variation Points
              if mpoint<=0%Prevent mutation from generating 0
                  mpoint=1;
              end
              if newpop(i,mpoint)==0%If the original point of variation is 0 then the variation is 1, otherwise the variation is 0.
                  newpop(i,mpoint)=1;
              else
                  newpop(i,mpoint)=0;
              end   
          end
      end
  end
  

• Select the next generation of individuals

  %Choice N The principle of screening is that individuals with higher suitability have a higher probability of being selected when they enter the next generation.
  function newPop = selection(pop,fitValue,N )
     totalFit=sum(fitValue);
     fitValue=fitValue/totalFit;%Probability of an individual being selected
     fitValue=cumsum(fitValue);%The sum of all the preceding elements of the corresponding element in the input for each element in the output
     [rows,cols]=size(pop);
     newPop=zeros(N,cols);
     isSelected=zeros(1,rows);%Is the record selected
     newin=1;
     while newin<N
         p=rand;
         for i=1:rows
             if ((isSelected(1,i)==0) && (p<=fitValue(i)))
                 isSelected(1,i)=1;
                 newin=newin+1;
                 newPop(newin,:)=pop(i,:);
                 break;
             end
         end
     end  
  end
  

• Record the most adaptable individuals

  %In this iteration, select the individuals with the highest fitness and their values
  function [bestIndividual,bestValue] = best( pop,fitValue,objValue)
     [rows,cols]=size(pop);
     bestIndividual=pop(1,:);
     bestFit=fitValue(1);
     for i=2:rows
         if fitValue(i)>bestFit
             bestIndividual=pop(i,:);
             bestFit=fitValue(i);
             bestValue=objValue(i);
         end
     end
  end
  

• Principal function

  function []= main( )
    clear;
    popSize=20;%Population Number
    chromLength=10;%Chromosome Length
    pc=0.7;%Crossover probability
    pm=0.005;%Probability of Variation
    iterators=200;%Number of iterations
    pop=initpop(popSize,chromLength);%Initialize Population
    y=zeros(1,iterators);
    x=zeros(1,iterators);
    maxValue=zeros(1,iterators);%Record the maximum value for each iteration
    for i=1:iterators
        newPop=crossover(pop,pc);%overlapping
        newPop=mutation(newPop,pm);%variation
        objValue=calobjvalue(newPop,chromLength);%Calculating individual objective function values
        fitValue=calfitvalue(objValue);%Calculate Individual Fitness
        [bestIndividual,bestValue]=best(newPop,fitValue,objValue);%Select the Individual with the Highest Fitness
        y(i)=bestValue;
        maxValue(1,i)=max(y);%Each iteration records the highest fitness individual value in this iteration
        x(i)=decodechrom(bestIndividual,1,chromLength)*10/1023;%Record the values in the variable domain of the most adaptable individual in this iteration
        pop=selection(newPop,fitValue,popSize);%Selecting Next Generation Individuals
    end
    fplot('10*sin(5*x)+7*cos(4*x)',[0,15]);
    hold on;
    plot(x,y,'r *');
    hold off;
    plot(maxValue);
  end
  

• Run Results
  • The position of the maximum value of each iteration in the original function image
    
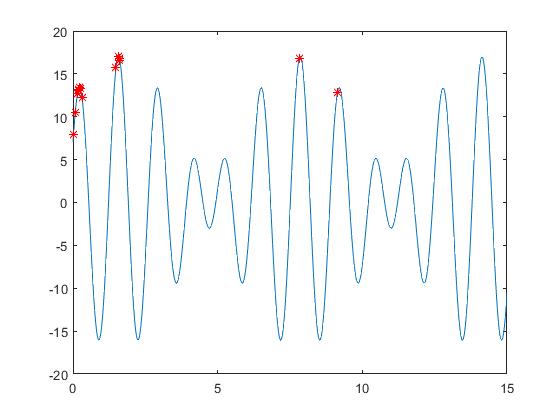
    Since the maximum value for each iteration is not necessarily greater than the maximum value for the previous iteration, there will be some duplication of values in the vector that records the maximum value.
  • Maximum change per iteration
    
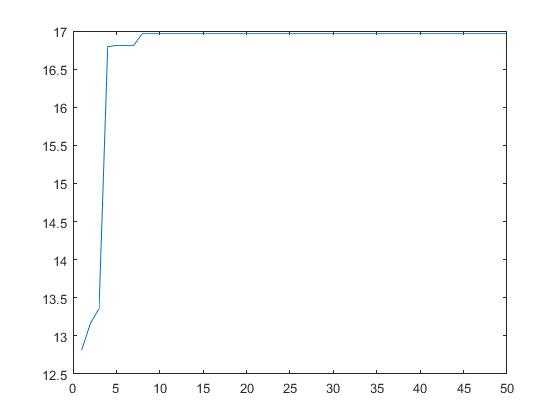
    You can see that as the number of iterations increases, it quickly converges near the maximum.