Concept:

Gauss elimination method:

Change the equations into upper triangle form:

When there is no solution / infinite solution / unique solution:

1. Perfect ladder: the only solution

2. Imperfect step: 0 = non-zero, no solution

3. Imperfect step shape: 0 = 0, infinite groups of Solutions

Specific methods:

For example, the following is a determinant:

The first step is to enumerate each column:

a) Find the row with the highest absolute value, the second row

b) Change the line to the top

c) Change the first number to 1

d) Cancel the current column of all the following rows to 0

After the first set of equations is completed, the first set of equations will be fixed. Starting from the second line, we will continue to find the line with the largest absolute value pair. Similarly, change the first number in the current column to 1:

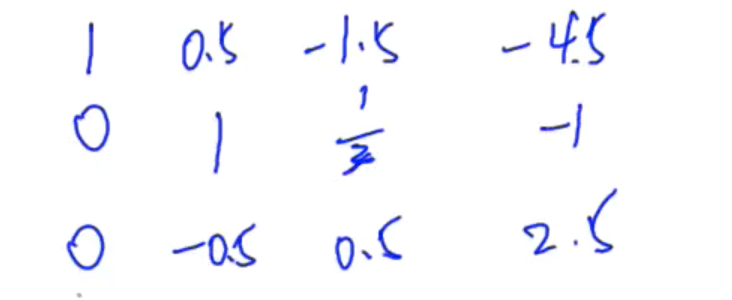
Similarly, the second number of the third line - 0.5 is reduced to 0:

We get the upper triangle structure with a unique solution. Then cancel each other:

Find the unique solution:

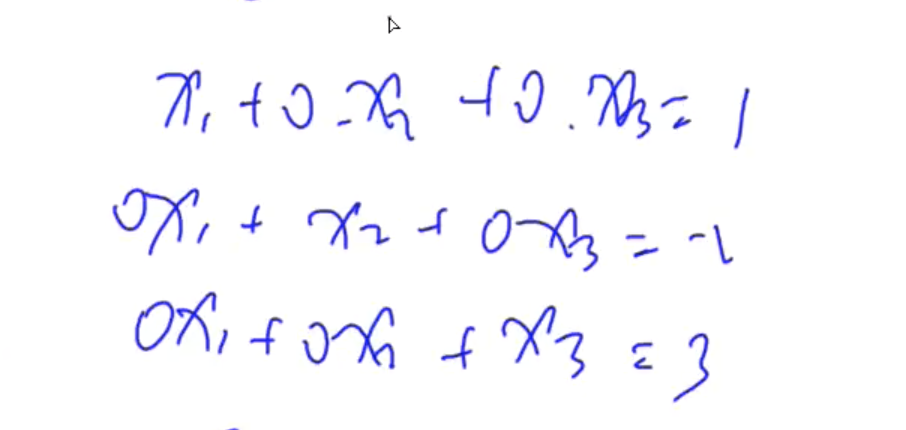
Example

Input a system of linear equations containing n equations and n unknowns.

The coefficients in the equations are real numbers.

Solve the equations.

The following figure is an example of a linear system of equations with m equations and n unknowns:

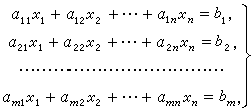
Input format

The first line contains the integer n.

Next n lines, each containing n+1 real numbers, represent the n coefficients of an equation and the constant to the right of the equal sign.

Output format

If there is a unique solution for a given system of linear equations, the total output is n lines, in which the i line outputs the solution of the i unknown number, and the result retains two decimal places.

If there are countless solutions for a given system of linear equations, "Infinite group solutions" is output.

If the given system of linear equations has No solution, output "No solution".

Data range

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;

const int N = 110;
const double eps = 1e-6;
int n;
double a[N][N];//Memory matrix

int gauss()
{
    int c, r;
    //1. From row 0, column 0, find the column with the highest absolute value
    for (c= 0, r = 0; c < n; c ++)
    {
        int t = r;
        for (int i = r; i < n; i ++)
            //If a column with larger absolute value is found, fabs represents absolute value function
            if (fabs(a[i][c] > fabs(a[t][c])))
                t = i;//Change to current column
        //Because the value is of double type, in order to prevent precision problems, we need to make a special judgment
        if (fabs(a[t][c]) < eps) continue;//fabs is to return the absolute value of floating-point number. If it is currently 0, return continue
        
        //2. Replace the line with the maximum absolute value
        for (int i= c; i <= n; i ++) swap(a[t][i], a[r][i]);
        //3. Change the first number of the line to 1
        //Change from the last
        for (int i = n; i >= c; i --) a[r][i] /= a[r][c];
        //4. Cancel the current column of all the following rows to 0
        for (int i = r + 1; i < n; i ++)
            if (fabs(a[i][c]) > eps)//From the second column, if the first number is greater than zero, cancel 0
                for (int j = n; j >= c; j --)//Pass the multiplication and division operation to the first row. Yes, the first number in the first row is the same as the first number in the second row, and then subtract
                    a[i][j] -= a[r][j] * a[i][c];//a[r][j] * a[i][c]: number of the first line * value of the first number of the first line I
        //Remember after operation++
        r ++;
    }
    if (r < n)//5. There may be no solution or infinite solutions
    {
        //If 0 = nonzero, there is no solution
        for (int i = r; i < n; i ++) 
            if (fabs(a[i][n]) > eps)//The last result of each line is > 0, i.e. if 0 = nonzero, there is no solution
                return 2;//unsolvable
        return 1;//Otherwise, there are infinite solutions
    }
    //6. Cancel the equation backwards, and the number after the first number will be zero
    for (int i = n - 1; i >= 0; i --)
        for (int j = i + 1; j < n; j ++)
            //Cancel from the last i
            //Remove all coefficients of the current equation except xi into 0, and subtract his coefficient * his value
            a[i][n] -= a[i][j] * a[j][n];//a[j][n] is the value of xj
    
    
    return 0;//If r = n, there is only one solution
}

int main()
{
    cin >> n;//N row n column
    for (int i = 0; i < n; i ++)
        for (int j = 0; j < n + 1; j ++)
            cin >> a[i][j];//Building input matrix
    
    //Gauss elimination
    int t = gauss();
    //Three solutions are obtained: unique solution, infinite multiple solutions and no solution
    if (t == 0)//t = 0 unique solution
    {
        for (int i = 0; i < n; i ++) printf("%.2f\n", a[i][n]);
    }//t = 1 infinite solutions
    else if (t == 1) puts("Infinite group solutions");
    //t = 2 no solution 
    else puts("No solution");
    
    return 0;
}

1≤n≤1001≤n≤100,
All input coefficients and constants shall be kept with two decimal places, and the absolute value shall not exceed 100.

Input example:

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

Output example:

1.00
-2.00
3.00