When designing the architecture of a distributed system, in order to improve the load capacity of the system, it is necessary to distribute different data to different service nodes. Therefore, we need a distribution mechanism, which is actually an algorithm to realize this function. Here we use the Consistent Hashing algorithm.
Before formally introducing the Consistent Hashing algorithm, let's first look at a simple hash algorithm, which uses the remainder to select nodes. The specific steps are as follows:
1, Create a hash table based on the number of nodes served by the cluster
2, Then, the integer hash value of the key name is calculated according to the key name, and the hash value is used to remainder the number of nodes.
3, Finally, the node is extracted from the hash table according to the remainder.
Suppose there are n server nodes in a cluster, and these nodes are numbered 0,1,2,..., n-1. Then, a piece of data (key,value) is stored in the server. At this time, how do we select the server node? According to the above steps, we need to calculate the hash value of key, and then take the remainder of n (number of nodes). The final value is the node we want. Expressed by a formula: num = hash (key)% n. hash() is a function to calculate the hash value. There are certain requirements for the hash() function here. If the hash() function we use is optimized, the calculated num is evenly distributed between 0,1,2,..., n-1, so that as many server nodes as possible can be used. Not all data is concentrated on one or several server nodes. The specific hash() implementation is not the focus of this chapter.
Although this simple remainder retrieval method is simple, it will have great problems if it is applied to the actual production system. Suppose we have 23 service nodes. According to the above method, the probability of a key mapping to each node is 1 / 23. If a service node is added, the previous hash (key)% n will become hash (key)% N + 1. In other words, there is a 23 / 24 probability that a key will be reassigned to a new node. On the contrary, only 1 / 24 of the probability will be assigned to the original node. Similarly, when you reduce one node, 22 / 23 probability will be reassigned to the new node.
In view of this situation, there needs to be a way to avoid or reduce the reduction of hit rate during horizontal expansion. This method is the Consistent Hashing algorithm we will introduce, which we call the consistent hash algorithm.
In order to understand how the Consistent Hashing algorithm works, we assume that the unit interval [0,1) is evenly distributed on the circle in a clockwise direction.
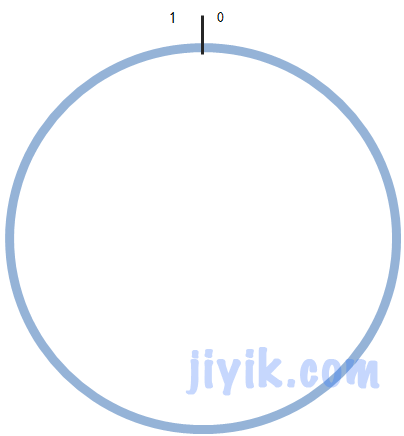
If there are n service nodes, the numbers of each service node are 0, 1, 2,..., n-1. Then we need a hash() function to calculate the hash value for the service node. If the value range returned by the hash() function is [0, R], then use the formula v = hash(n) / R. the resulting V will be distributed in the unit interval [0, 1). Therefore, in this way, our service nodes can be distributed on the circle.
Of course, drawing a circle in the unit interval [0,1] is only one way. There are many other ways to draw a circle. For example, take the interval [0,2 ^ 32-1) as a circle, and then use the hash() function to calculate the hash() value for the service node. Of course, the value generated by the selected hash() function must also be within the range of 0 – (2 ^ 32-1).
Let's take [0,1) as an example.
We take three service nodes as an example
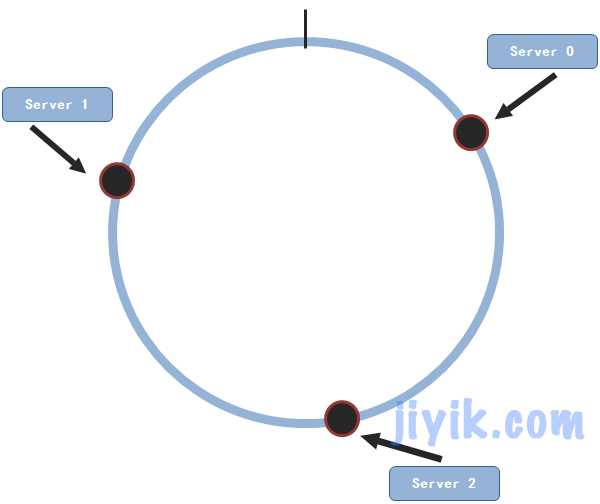
The three nodes are randomly distributed on the circle. Now suppose we have a piece of data (key,value) to store. The next thing to do is to map the data to the circle in the same way.
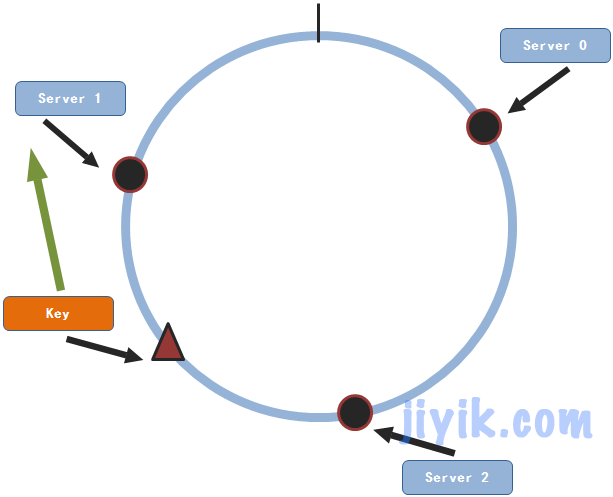
Then, start from the position where the key is located on the circle and find the position of the service node clockwise. The first service node found is the node to be stored. Therefore, this data will be stored on service node 1.
Similarly, when other (key,value) pairs need to be stored, select the service node according to the above method.
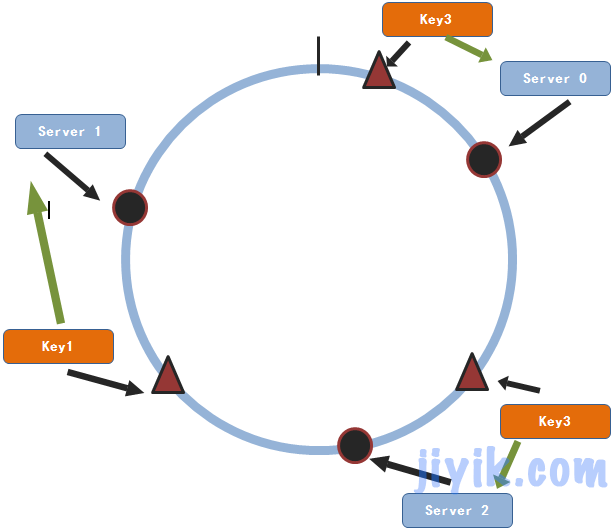
Now let's see if this method can solve the horizontal expansion problem we just mentioned?
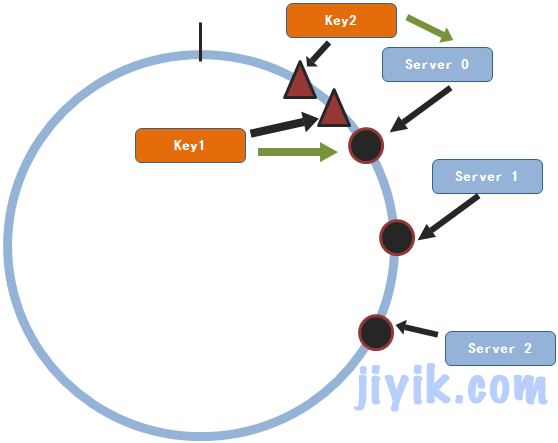
Suppose we need to add a service node 3

From the above figure, we can see that only key1 will change its storage service node. For most data, the original node will still be found. Therefore, for a cluster with n service nodes, when there are more service nodes, a piece of data will only be 1/(n+1) This probability is much smaller than the probability obtained by the remainder method. Similarly, the principle of reducing a service node and increasing a service node is the same, and the probability of re selecting a service node for each data is 1/(n-1). Similarly, this probability is also very small.
Here is a php code to simply implement this process
$nodes = array('192.168.5.201','192.168.5.102','192.168.5.111'); $keys = array('onmpw', 'jiyi', 'onmpw_key', 'jiyi_key', 'www','www_key','key1'); $buckets = array(); //Nodal hash Dictionaries $maps = array(); //storage key Mapping relationship between and nodes /** * Generate node Dictionary -- distribute nodes on the circle of unit interval [0,1] */ foreach( $nodes as $key) { $crc = crc32($key)/pow(2,32); // CRC To move $buckets[] = array('index'=>$crc,'node'=>$key); } /* * Sort by index */ sort($buckets); /* * hash each key to find its position on the circle * Then start at this location and find the first service node in a clockwise direction */ foreach($keys as $key){ $flag = false; //Indicates whether a service node has been found $crc = crc32($key)/pow(2,32);//calculation key of hash value for($i = 0; $i < count($buckets); $i++){ if($buckets[$i]['index'] > $crc){ /* * Because buckets have been sorted * Therefore, the first node whose index is greater than the hash value of the key is the node to be found */ $maps[$key] = $buckets[$i]['node']; $flag = true; break; } } if(!$flag){ //If not found, use buckets First service node in $maps[$key] = $buckets[0]['node']; } } foreach($maps as $key=>$val){ echo $key.'=>'.$val,"<br />"; }
The result of this code is as follows
onmpw=>192.168.5.102 jiyi=>192.168.5.201 onmpw_key=>192.168.5.201 jiyi_key=>192.168.5.102 www=>192.168.5.201 www_key=>192.168.5.201 key1=>192.168.5.111
Then we add a service node and modify the code as follows
$nodes = array('192.168.5.201','192.168.5.102','192.168.5.111','192.168.5.11');
Other codes remain unchanged, continue to run, and the results are as follows
onmpw=>192.168.5.102 jiyi=>192.168.5.201 onmpw_key=>192.168.5.11 jiyi_key=>192.168.5.102 www=>192.168.5.201 www_key=>192.168.5.201 key1=>192.168.5.111
We can see that only onmpw_key reselects the service node. The others are the original nodes.
Here we see that the hit probability is much higher than that of the remainder method. Does this solve the problem we encountered earlier?
Actually, not yet. After all, the distribution of these values is not so uniform. In the system, the distribution of these service nodes may be very centralized, which may lead to the situation that all key s are mapped to one or several nodes, and the remaining service nodes are not used. Although this is not a very serious problem, why do we waste Even if it's just a server.
In our view, this situation causes the data to be concentrated on one service node, resulting in the waste of other service nodes. So how to solve this problem? People have come up with a new way: to establish virtual nodes for each node. What do you mean? That is, for node j, m replicas are created. The M copied nodes get different hash values through the hash() function, but the node information saved by each virtual node is node j. Then these virtual nodes are randomly distributed on the circle. For example, we have two service nodes. And three virtual nodes are copied for each node. These nodes (including virtual nodes are randomly distributed on the circle)

In this way, it seems that the service nodes are evenly distributed on the circle. In fact, to sum up, the above method is slightly improved - copy some virtual nodes for each node.
Therefore, our code does not need to be modified too much. In order to see the code more intuitively, I still list the whole code here.
$nodes = array('192.168.5.201','192.168.5.102','192.168.5.111'); $keys = array('onmpw', 'jiyi', 'onmpw_key', 'jiyi_key', 'www','www_key','key1'); //Where the added variable is modified $replicas = 160; //Number of replications per node $buckets = array(); //Nodal hash Dictionaries $maps = array(); //storage key Mapping relationship between and nodes /** * Generate node Dictionary -- distribute nodes on the circle of unit interval [0,1] */ foreach( $nodes as $key) { //Place of modification for($i=1;$i<=$replicas;$i++){ $crc = crc32($key.'.'.$i)/pow(2,32); // CRC To move $buckets[] = array('index'=>$crc,'node'=>$key); } } /* * Sort by index */ sort($buckets); /* * hash each key to find its position on the circle * Then start at this location and find the first service node in a clockwise direction */ foreach($keys as $key){ $flag = false; //Indicates whether a service node has been found $crc = crc32($key)/pow(2,32);//calculation key of hash value for($i = 0; $i < count($buckets); $i++){ if($buckets[$i]['index'] > $crc){ /* * Because buckets have been sorted * Therefore, the first node whose index is greater than the hash value of the key is the node to be found */ $maps[$key] = $buckets[$i]['node']; $flag = true; break; } } if(!$flag){ //If not found, use buckets First service node in $maps[$key] = $buckets[0]['node']; } } foreach($maps as $key=>$val){ echo $key.'=>'.$val,"<br />"; }
The changes have been marked out in the code. You can see that there are still few changes.
So far, I believe you should have a clear understanding of Consistent Hashing. hash algorithm is still very useful, such as memcache cluster, nginx load and so on.
We are Take you to a deeper understanding of distributed thinking in Memcached This article introduces the application of consistency hash algorithm in Memcache with a practical case. All our code here is implemented in PHP. If you are not familiar with PHP and are interested, you can refer to the following tutorial, PHP tutorial.
Therefore, understanding the hash algorithm is of great help to us.
The expression of the above algorithm process is unclear or inappropriate. You are welcome to comment.