Full permutation (with recursive and non-recursive solutions)

Keywords: network

Author: bakari

Time: 8.2-23:48, 2012

Reprinted from: http://www.cnblogs.com/bakari/archive/2012/08/02/2620826.html Thank you!

Full permutation appears frequently in written examinations of major network companies in recent years

First, let's see how the title is required (Baidu Xunlei school signature test).

Write a function in C++, such as Foo(const char *str), and print out the full list of strs.

For example, the full arrangement of abc: abc, acb, bca, dac, cab, cba

1. Recursive Version

1. Brief algorithm description

Simply put: the first number is exchanged after the subsequent number

E.g:E = (a,b,c), then prem(E) = a.perm(b,c) + b.perm(a,c) + c.perm(a,b)

Then a.perm(b,c) = a b.perm(c) + a c.perm(b) = a B C + a C B.

Well, it's not difficult to compile a good code once you know the algorithm.

2. Code reference

1 Foo(const char *str)
2 {
3     Perm( str , 0 , strlen( str ) – 1 );
4 }

 1 //Three parameters are required, k Represents the current number, m Number of Representations
 2 Perm( char *pszStr , int k , int m ) 
 3 {
 4       if (k == m)  
 5       {  
 6            static int s_i = 1;  
 7            cout<<" No.<<s_i ++<<" Arrangement"<<pszStr<<endl;
 8      }  
 9      else
10      {  
11            for (int i = k; i <= m; i++) //No. i New permutations can be obtained by swapping numbers behind each other
12            {  
13                   Swap(pszStr + k, pszStr + i);  
14                   Perm(pszStr, k + 1, m);  
15                   Swap(pszStr + k, pszStr + i);  
16            }  
17       } 
18 }

3. See the picture to know

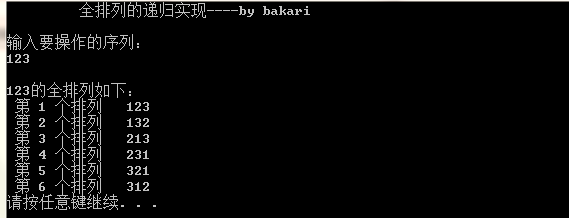
However, there is a small drawback: two identical numbers are also exchanged, as shown in the following figure:

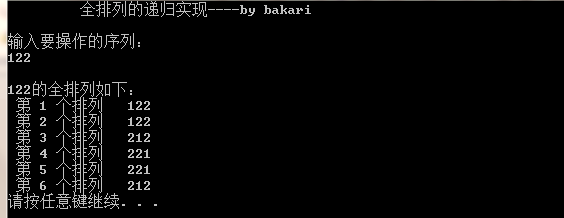
Obviously, this is definitely not what you want:

4. Code Improvement

Remove the full arrangement of duplicate symbols: before exchanging, you can first judge whether two symbols are the same, not the same before exchanging. This time you need a function to determine whether the symbols are the same.

bool IsSwap(char *pszStr, int nBegin, int nEnd)  
{  
       for (int i = nBegin; i < nEnd; i++) 
       if (pszStr[i] == pszStr[nEnd])  
             return false;  
       return true;  
}

So the improved code is as follows:

 1 Perm(char *pszStr, int k, int m)  
 2 {  
 3      if (k == m)  
 4      {  
 5           Static int s_i = 1;  
 6           cout<<" No.<<s_i ++<<" Arrangement"<<pszStr<<endl;
 7      }  
 8      else
 9      {  
10           for (int i = k; i <= m; i++) //No. i New permutations can be obtained by swapping numbers behind each other
11           {  
12                 if (IsSwap(pszStr, k, i))   //Added statement to determine equality
13                 {  
14                       Swap(pszStr + k, pszStr + i);  
15                       Perm(pszStr, k + 1, m);  
16                       Swap(pszStr + k, pszStr + i);  
17                 }  
18            }  
19       }  
20 }

OK, see picture

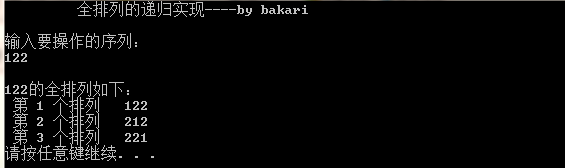
2. Non-recursive versions

1. Brief algorithm description

To consider a non-recursive implementation of full permutation, consider first how to compute the next permutation of a string.For example, the next permutation of "1234" is "1243".As long as you repeatedly find the next arrangement of strings, the entire arrangement will be solved.

How do I calculate the next permutation of strings?Considering the string "926520", we look backwards and forwards for the first pair of adjacent incremental numbers, "20", "52" are non-incremental, "26""That is to say, the previous number 2 is the replacement number, the subscript of the replacement number is called the replacement point, and then find a minimum number larger than the replacement number from the back (this number must exist). 0, 2 cannot, 5 can exchange 5 and 2 to"956220". Then, the string after the replacement point"6220"is inverted to"950226".

If you reach the maximum of this number, such as 1234-4A4321, then you end the cycle.

If the input is a non-minimum number, such as 1324, it is converted to the minimum number, such as 1234, and sorted.Sorting algorithms use fast queuing, you can write one yourself. If fast queuing doesn't work, you can look at it first and then look at it again, or you can think of a reliable algorithm yourself, or you can use qsort (s, n, sizeof (s[0]), cmp) in the VC library directly; just spend a little more time below for what each parameter means.

OK, see Code Analysis below

2. Code Analysis

 1 Prem( char *s )   //Full permutation function
 2 {
 3     char *pEnd = s + strlen(s) - 1;
 4     char *p = pEnd;  //p Represents a replacement point
 5     //q Represents the next number of replacement points, pMax Represents the minimum number greater than the replacement point
 6     char *q = new char,*pMax = new char;  //Attention to initialization!!!
 7     while (p !=  s)          //p == s End the loop
 8     {
 9         q = p;
10         p--;
11         if (*p < *q)
12         {
13             pMax = FindMaxForOne(p,pEnd);  //Find Points Exchanged with Replacement Points
14             Swap(p,pMax);         //exchange
15             Reverse(q,pEnd);       //Reverse all numbers after replacing points
16             Print(s);              //output
17             p = pEnd;             //Place the replacement point at the last point and start the next cycle
18         }
19         if (s == p) break;           //End condition
20     }
21 }

There are several functions involved above

Tell me about the function of finding the number that is exchanged with the number of substitutions

1 char* FindMaxForOne(char *p,char *q)
2 {
3     char *p1 = p;
4     char *p2 = q;
5     while (*p2 <= *p1) p2--;
6     return p2;
7 }

!!!Here we want to explain: the first number that is larger than the number of substitutions to look for from back to front must be the minimum number to look for. Why, this taste slowly, I also encounter some difficulties when I do it. I will not easily remember it without experience.

The other functions are little case s.I wish you success!

3. See the picture to know

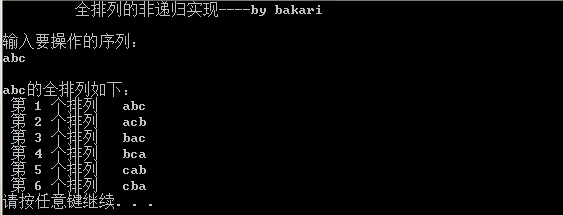
3. There is a method for non-recursive return

Description: Unlike the previous one, this algorithm is cumbersome, but understandable, and does not require the output to be arranged so strictly from small to large as the previous one.

First swap the output of the last number from right to left, then judge if the number is a cardinal number, swap the two numbers farthest from the number, then swap the output of the first number from left to right, swap the two numbers at the far end, so that the whole number can be arranged in a loop.This may be abstract, let's take an example:

　　E.g: 　　　1 2 3 4

First time: (from right to left): 1 2 4 3 --- 1 2 4 3 --- 1 4 2 3 --- 4 1 2 3 --- 4 1 2 3 Move the last number forward one by one

Exchange: 2 and 3 ---> 41 3 2

Second time: (from left to right): 4 1 3 2 --- 1 4 3 2 --- 1 3 4 2 --- 1 3 2 --- 1 3 2 4 4 4 Move the first number back in turn

Exchange: 1 and 3 --> 3 1 2 4 Repeat for the first time until all numbers are output

Look at the code:

 1 /************************************************************************
 2  *   Author: bakari 
 3  *   Date:   2011.5.7
 4 /************************************************************************/
 5 int n;
 6 void swap(int *a,int *b);    //Exchange function 
 7 void print(int a[]);         //Number of groups after printing interchange 
 8 int jfc();                   //Finding factorial function 
 9 int jmp(int n);              //Jump function 
10 void sort(int a[]);          //Full permutation function 
11 
12 int main(){
13     while(cin>>n)
14     {
15         while(n<=0)
16         {
17             cout<<"Error in input!Please re-enter: ";
18             cin>>n;
19         }
20         int *a=new int[n];
21         for(int i=0;i<n;i++)
22             a[i]=i+1;
23         sort(a);
24         delete []a;
25     }
26     system("pause");
27     return 0;
28 }
29 
30 void swap(int *a,int *b)
31 {
32     int t=*a;
33     *a=*b;
34     *b=t;
35 }
36 void print(int a[])
37 {
38     for(int i=0;i<n;i++)
39         cout<<a[i]<<' '; 
40     cout<<endl;
41 
42 }
43 int jfc()
44 {
45     int s=1;
46     for(int i=1;i<=n;i++)
47         s*=i;
48     return s;
49 }
50 int jmp(int n)
51 {
52     if(n>jfc())
53         return 0;
54 }
55 void sort(int a[])
56 {
57     int m=1,count=0;                   //m Count the number of full permutations,count Count rows 
58     int *p1,*p2;
59     for(p1=a+n-1,p2=a+n-2;p1>=a+1,p2>=a;p1--,p2--)
60     {
61         print(a);
62         swap(p1,p2);
63         m++;
64     } 
65     count++;
66     while(m<=jfc()){
67         if(count%2)
68         {   print(a);
69         swap(&a[n-1],&a[n-2]);
70         m++;
71         if(!jmp(m))
72             break;
73         for(p1=a,p2=a+1;p1<=a+n-2,p2<=a+n-1;p1++,p2++)
74         {
75             print(a);
76             swap(p1,p2);
77             m++;
78         }
79         count++;
80         }
81         else
82         {
83             print(a);
84             swap(&a[0],&a[1]);
85             m++;
86             if(!jmp(m))
87                 break;
88             for(p1=a+n-1,p2=a+n-2;p1>=a+1,p2>=a;p1--,p2--)
89             {
90                 print(a);
91                 swap(p1,p2);
92                 m++;
93             }
94             count++;
95         }
96 
97     } 
98     cout<<"Share"<<m-1<<"Species Arrangement"<<endl;
99 }

The key is to master both!

IV. Summary

So far, we have used both recursive and non-recursive methods to solve the full permutation problem. To sum up, this is:

1. Full permutation is the exchange of each number from the first number to the number after it.

2. The full arrangement of de-weighting is the exchange of each number from the first number with a number that does not repeat after it.

3. Full permutation is a non-recursive process in which the number of substitutions and replacement points are searched backward and forward, then the first number larger than the number of substitutions is exchanged with the number of substitutions backward and forward, and all the data after the replacement points are reversed.

* On * 8/2 - 23:48

Make sure you burn more fragrance.

We have opened a public number, aCloudDeveloper, dedicated to dry technology sharing and look forward to meeting you.

Posted by AshrakTheWhite on Sun, 10 May 2020 19:09:20 -0700

Programmer Group

Full permutation (with recursive and non-recursive solutions)

Hot Keywords