/*

• @Author: yang
• @Date: 2021-09-27 19:40:34
• @LastEditors: yang
• @LastEditTime: 2021-10-19 19:57:43
• @FilePath: \demo \ breadth first traversal. js
  */

Front end "N Queen" recursive backtracking classical problem

Let's look at the problem first. In fact, the problem is not difficult to understand:
The n queen problem studies how to place n queens in n × N's chessboard, and the Queens can't attack each other
Given an integer n, returns the solution of all different N Queen problems.
Each solution includes an explicit chess placement scheme for the n queen problem, in which 'Q' and '.' represent the queen and the empty space respectively.
Example:
Input: 4
Output:[
[". Q...", / / solution 1
"...Q",
"Q...",
"...Q."],

["... Q.", / / solution 2
"Q...",
"...Q",
".Q..."]
]
The queen is a chess piece in chess, which means the king's wife. The queen only does one thing, that is, "eat the pieces". When she meets a piece that can be eaten, she quickly rushes up and eats the pieces. Of course, she can walk one to seven steps horizontally, vertically and obliquely.
thinking
At first glance, this problem of selecting all the schemes is a little difficult to find out, but in fact, if you take a closer look, the problem has limited that Queens can not attack each other. In fact, the language transformed into code thinking means that there can only be one queen in each line and one queen in each diagonal line,
in other words:

On one column, wrong.

[
'Q', 0
'Q', 0
]
Copy code
On the diagonal of upper left - > lower right, wrong.

[
'Q', 0
0, 'Q'
]
Copy code
On the bottom left - > top right diagonal, wrong.

[
0, 'Q'
'Q', 0
]

Then, based on this idea, we can turn this problem into a problem of "placing queens line by line", and think about how to design recursive functions?

For the solution of Queen n, we can design a function that accepts the following parameters:

1. The rowIndex parameter represents the row on which you are currently trying to place the queen
2. The prev parameter represents the queen position of the previous row. For example, [1,3] represents that the queen of row 0 (array subscript) is placed in position 1, and the queen of the first row is placed in position 3
   When rowIndex === n, it means that the recursion successfully placed n queens and reached the destination unimpeded. Each placement successfully passed our constraints
   Then put the prev as a result into the global res result array

realization
Ideals are always beautiful. Although our ideas are very clear so far, we will still encounter several headache problems in specific coding.

After a queen has fallen in the current line, the next line needs to judge three conditions:

1. You can't put queens on this line before
   2. The queen cannot be placed before diagonal line 1, that is, [lower left - upper right]
   3. The queen cannot be placed before diagonal 2, that is, [upper right - > lower left]

Diagonal 1

Add the vertical and horizontal coordinates rowIndex + columnIndex directly through this point. If they are equal, they are on the same diagonal 1
Diagonal 1:
2n-1
i+j

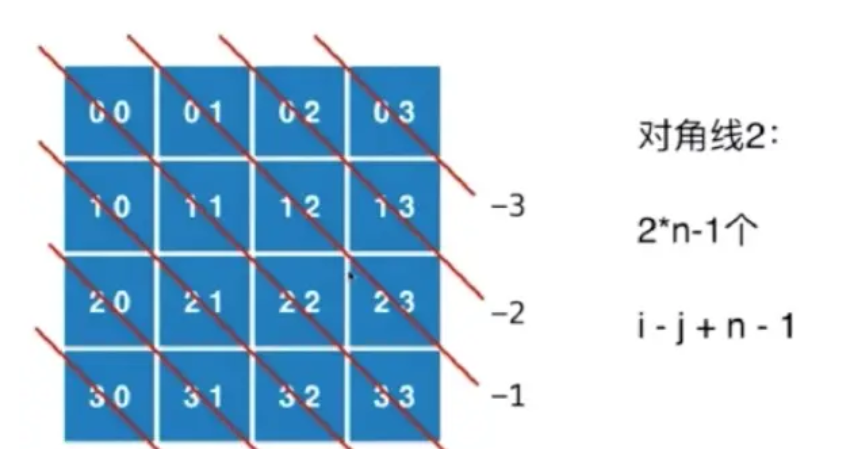
Diagonal 2

Subtract directly from the abscissa and ordinate rowIndex - columnIndex of this point. If it is equal, it is on diagonal 2
Diagonal 2:
2*n - 1
i - j + n - 1

So:
1. Use the column subscript placed by the columns data record, and then directly mark it as true
2 use dia1 array to record the placed diagonal 1 subscript. After placement, directly mark the subscript rowIndex + columnIndex as true
3 use dia2 array to record the placed diagonal 2 subscripts. After placing the subscripts, directly mark the subscript rowIndex - columnIndex as true
4. The parameter prev of the recursive function represents the number of columns placed by the queen in each row. For example, prev[0] = 3 represents that the queen in row 0 is placed in column 3, and so on
5 before entering the recursive function each time, mark the subscript of diagonal 1 and diagonal 2 of the column corresponding to the current item as true, and enter the recursive function with the marked state
After this recursion, you need to reset these states to false before entering the next cycle

With these auxiliary knowledge points, we can start writing recursive functions. In each line, we constantly try a coordinate point. As long as it does not conflict with the previous results, it can be put into the array as the starting value of the next recursion
In this way, if the recursive function successfully comes to the case of rowIndex === n, it indicates that all the previous conditions meet the solution of an n queen, and the prev one-dimensional array is generated. Restore the prev one-dimensional array to the two-dimensional array required by the topic through the auxiliary function

/**
 * @param {number} n
 * @return {string[][]}
 */

let solveNQueens = function(n){
    let res = []
    // The column subscript of the queen has been placed
    let columns = []
    // Diagonal 1 subscript of placed queen lower left - > upper right
    // The way to calculate whether a coordinate is on this diagonal is whether [row subscript + column subscript] is equal
    let dia1 = []
    // Diagonal 2 subscript of placed Queen: upper left - > lower right
    // The way to calculate whether a coordinate is on this diagonal is whether [row subscript column subscript] is equal
    let dia2 = []
    //  Record the status after selecting the current grid
    let record = (rowIndex,columnIndex,bool)=>{
        columns[columnIndex] = bool
        dia1[rowIndex + columnIndex] = bool
        dia2[rowIndex - columnIndex] = bool
    }
    // Try placing the Queen's position in line index in an n Queen's question
    let putQueen = (rowIndex,prev)=>{
        if(rowIndex === n){
            res.push(generateBoard(prev))
            return 
        }

        // Attempt to place the [0,n-1] column of row Index
        for(let columnIndex = 0; columnIndex <n;columnIndex++){
            // No conflicts on columns
            let columnNotConflict = !columns[columnIndex]
            // No conflict on diagonal 1
            let dia1NotConflict = !dia1[rowIndex + columnIndex]
            // No conflict on diagonal 2
            let dia2NotConflict = !dia2[rowIndex - columnIndex]
            if(columnNotConflict&&dia1NotConflict&&dia2NotConflict){
                // If there is no conflict, record the current selected position first and enter the next round of recursion
                record(rowIndex,columnIndex,true)
                putQueen(rowIndex + 1,prev.concat(columnIndex))
                // After recursion out of the stack, clear the record of this position in the state. The next cycle should be a new start
                record(rowIndex,columnIndex,false)
            }
        }
    }
    putQueen(0,[])
    return res
}


//Auxiliary function for generating two-dimensional array
function generateBoard(row){
    let n = row.length
    let res = []
    for(let y = 0; y<n;y++){
        let cur = ""
        for(let x = 0; x<n;x++){
            if(x === row[y]){
                cur += "Q"
            }else{
                cur += "."
            }
        }
        res.push(cur)
    }
    return res
}