1. Overview of integer split items
1.1 1 * 2 + 2 * 3 + 3 * 4 + ... + (n - 1) * n = ?
Solution: The split term formula is:
(n - 1) * n = [(n - 1) * n * (n + 1) - (n - 2) * (n - 1) * n] / 3
The solution process is shown in the following figure:

1.2 1 * 2 * 3 + 2 * 3 * 4 + 3 * 4 * 5 + ... + (n - 2) * (n - 1) * n = ?
Solution: The split term formula is:
(n - 2) * (n - 1) * n = [(n - 2) * (n - 1) * n * (n + 2) - (n - 3) * (n - 2) * (n - 1) * n] / 4
The solution process is shown in the following figure:

1.3 1 * 3 + 3 * 5 + 5 * 7 + ... + 19 * 21 = ?
Solution: Note that in the two factors of each addend, the tolerance is 2. The solution process is shown in the following figure:

1.4 5 * 10 * 15 + 10 * 15 * 20 + ... + 40 * 45 *50 = ?
Solution: Note that in the three factors of each addend, the tolerance is 5. The solution process is shown in the following figure:
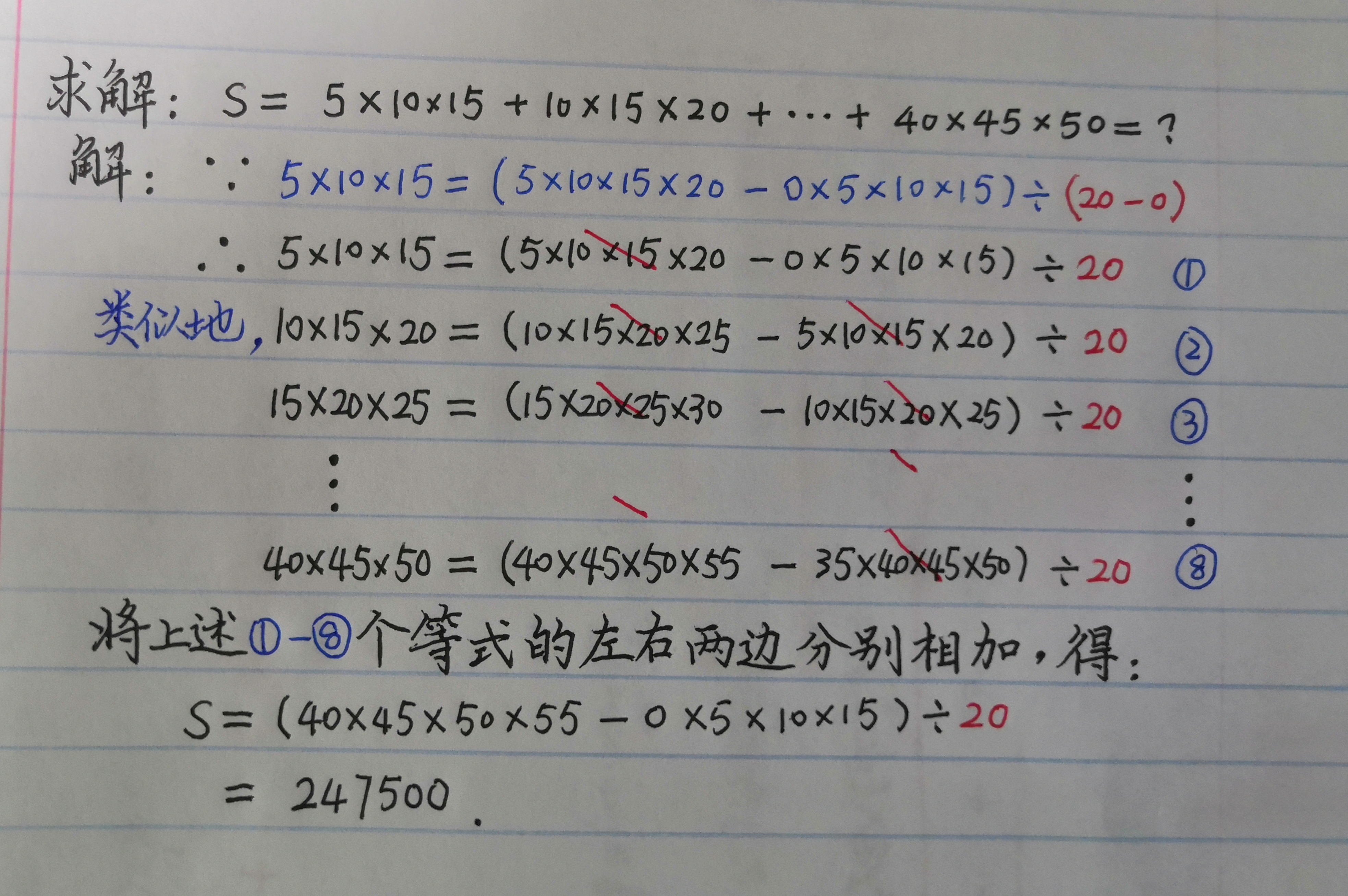
2. About 1 * * 2 + 2 * * 2 + 3 * * 2 + ... + n**2 = n * (n + 1) * (2n +1) / 6 proof of
The key points of the certificate are:
n ** 2 = n ** 2 - 1 + 1
= n ** 2 - 1 ** 2 + 1
= (n - 1) * (n + 1) + 1
The certification process is shown in the figure below:

3. Solution of 1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 +... + 97 * 98 * 99 * 100 =
The solution of this kind of problem is much more complex than the previous problem, because in two adjacent addends, the factor does not meet the continuity of the directly separable term, that is:
1 * 2 * 3 * 4 + 2 * 3 * 4 * 5
It satisfies the continuity of the directly separable term, but
1 * 2 * 3 * 4 + 3 * 4 * 5 * 6
It doesn't satisfy the continuity of directly divisible items. What should I do?
The typical idea is to construct a sequence that satisfies the continuity of the direct splitting term, and then solve it indirectly by solving the equations.
Before solving, let's use a very hard core Solver (violent accumulation) to see what the result is.
3.1 hard core solver
- foo.py (simple and rough algorithm)
1 #!/usr/bin/python3 2 """ Question: 3 1 * 2 * 3 * 4 + 4 3 * 4 * 5 * 6 + 5 5 * 6 * 7 * 8 + 6 ... + 7 97 * 98 * 99 * 100 8 = 9 4! 6! 8! 100! 10 ---- + ---- + ---- + ... + ----- 11 0! 2! 4! 96! 12 = ? 13 """ 14 import sys 15 16 17 def main(argc, argv): 18 if argc < 2: 19 print("Usage: %s <N> [-D]" % argv[0], file=sys.stderr) 20 print("e.g.", file=sys.stderr) 21 print(" %s 96" % argv[0], file=sys.stderr) 22 print(" %s 96 -D" % argv[0], file=sys.stderr) 23 return 1 24 25 n = int(argv[1]) 26 if argc == 3 and argv[2] == '-D': 27 debug = True 28 else: 29 debug = False 30 31 a = [] 32 i = 0 33 s = 0 34 while i <= n: 35 x = (i + 1) * (i + 2) * (i + 3) * (i + 4) 36 a.append('%d * %d * %d * %d' % (i + 1, i + 2, i + 3, i + 4)) 37 s += x 38 i += 2 39 if debug: 40 print('%s = %d' % (' + '.join(a), s)) 41 else: 42 b = [a[0], a[1], a[2], '...', a[-1]] 43 print('%s = %d' % (' + '.join(b), s)) 44 45 return 0 46 47 48 if __name__ == '__main__': 49 sys.exit(main(len(sys.argv), sys.argv))
- Run foo.py
huanli@idorax16:~$ ./foo.py 96 -D 1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 + 7 * 8 * 9 * 10 + 9 * 10 * 11 * 12 + 11 * 12 * 13 * 14 + 13 * 14 * 15 * 16 + 15 * 16 * 17 * 18 + 17 * 18 * 19 * 20 + 19 * 20 * 21 * 22 + 21 * 22 * 23 * 24 + 23 * 24 * 25 * 26 + 25 * 26 * 27 * 28 + 27 * 28 * 29 * 30 + 29 * 30 * 31 * 32 + 31 * 32 * 33 * 34 + 33 * 34 * 35 * 36 + 35 * 36 * 37 * 38 + 37 * 38 * 39 * 40 + 39 * 40 * 41 * 42 + 41 * 42 * 43 * 44 + 43 * 44 * 45 * 46 + 45 * 46 * 47 * 48 + 47 * 48 * 49 * 50 + 49 * 50 * 51 * 52 + 51 * 52 * 53 * 54 + 53 * 54 * 55 * 56 + 55 * 56 * 57 * 58 + 57 * 58 * 59 * 60 + 59 * 60 * 61 * 62 + 61 * 62 * 63 * 64 + 63 * 64 * 65 * 66 + 65 * 66 * 67 * 68 + 67 * 68 * 69 * 70 + 69 * 70 * 71 * 72 + 71 * 72 * 73 * 74 + 73 * 74 * 75 * 76 + 75 * 76 * 77 * 78 + 77 * 78 * 79 * 80 + 79 * 80 * 81 * 82 + 81 * 82 * 83 * 84 + 83 * 84 * 85 * 86 + 85 * 86 * 87 * 88 + 87 * 88 * 89 * 90 + 89 * 90 * 91 * 92 + 91 * 92 * 93 * 94 + 93 * 94 * 95 * 96 + 95 * 96 * 97 * 98 + 97 * 98 * 99 * 100 = 974510040 huanli@idorax16:~$ ./foo.py 96 1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 + ... + 97 * 98 * 99 * 100 = 974510040
Before formally solving this problem, let's start with a simpler problem. For example:
1 * 2 + 3 * 4 + 5 * 6 + ... + 99 * 100 = ?
3.2 solution of 1 * 2 + 3 * 4 + 5 * 6 +... + 99 * 100 =
- The solution result with Python code is as follows:
>>> s = 0 >>> i = 1 >>> while i <= 99: ... x = i * (i + 1) ... s += x ... i += 2 ... >>> s 169150
- The solution process of the equations based on integer split term + construction is as follows:

3.3 about 1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 +... + 97 * 98 * 99 * 100 =? Solution
This problem is a Mathematical Olympiad problem in Grade 6 of primary school. It is very difficult and challenging for students in Grade 6 of primary school. With the foundation of 3.2, the next solution idea is very clear, but the solution process needs to be reduced step by step.
The solution process is as follows:
4. Conclusion
To be continued...