Five python methods of Fibonacci sequence
Fibonacci sequence, also known as golden section sequence, was introduced by mathematician Leonardo Fibonacci with rabbit breeding as an example, so it is also called "rabbit sequence", referring to such a sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34 Mathematically, Fibonacci sequence is defined recursively as follows: F(1)=1, F(2)=1, F(n)=F(n-1)+F(n-2) (n > = 2, n ∈ n *)
Fibonacci sequence, the difficulty lies in the algorithm, and if it becomes a generator, it needs to use for loop to traverse the iterative generator
The first method of recursion
def fib_recur(n):
assert n >= 0, "n > 0"
if n <= 1:
return n
return fib_recur(n-1) + fib_recur(n-2)
for i in range(1, 20):
print(fib_recur(i), end=' ')The writing method is the most concise, but the efficiency is the lowest, there will be a lot of repeated calculations, time complexity O (1.618^n), and the deepest 1000
The second recurrence method
def fib_loop(n):
a, b = 0, 1
for i in range(n+1):
a, b = b, a+b
return a
for i in range(20):
print(fib_loop(i), end=' ')The recurrence method is the incremental method. The time complexity is O(n), and it grows linearly. If the amount of data is huge, the speed will be slower and slower
Third generator
def fib_loop_while(max):
a, b = 0, 1
while max > 0:
a, b = b, a+b
max -= 1
yield a
for i in fib(10):
print(i, end=' ')Functions with yield are considered as generators, which are iteratable objects, and have "iter" and "next" methods, which can traverse to get elements
The fourth way to achieve internal magic
class Fibonacci(object):
def __init__(self, num):
self.num = num
def __iter__(self):
if self.num < 1:
return 1
a, b = 0, 1
while self.num > 0:
a, b = a + b, a
self.num -= 1
yield a
def __next__(self):
return self.__iter__()
f = Fibonacci(15)
for i in f:
print(i)Fifth matrix
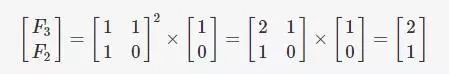
### 1
import numpy
def fib_matrix(n):
res = pow((numpy.matrix([[1, 1], [1, 0]])), n) * numpy.matrix([[1], [0]])
return res[0][0]
for i in range(10):
print(int(fib_matrix(i)), end=' ')
### 2
# Using matrix to calculate Fibonacci series
def Fibonacci_Matrix_tool(n):
Matrix = npmpy.matrix("1 1;1 0")
# Return is matrix type
return pow(Matrix, n) # pow function is faster than binary star**
def Fibonacci_Matrix(n):
result_list = []
for i in range(0, n):
result_list.append(numpy.array(Fibonacci_Matrix_tool(i))[0][0])
return result_list
# call
Fibonacci_Matrix(10)Because power operation can be accelerated by dichotomy, the time complexity of matrix method is O(log n)
Using scientific calculation package numpy to realize matrix method O(log n)