The minimum spanning tree is the one with the least weight. (acyclic, the graph connecting all vertices must be a tree, i.e. spanning tree)
GENERIC-MST

In each step of the algorithm, an edge (u, v) is determined, so that after adding it to set a, a & {(u, v)} is still a subset of a minimum spanning tree. We call such an edge the safe edge of A.
The key of the algorithm is how to find the safe side.
Understanding: cut, light edge, cross, aspects
Graph Segmentation:
One kind of graph segmentation is to divide all vertices into two non empty and non repeated sets. A crosscut edge is an edge that connects two vertices that belong to different sets.
Segmentation theorem:
In a weighted graph, given any segmentation, the one with the least weight in its cross cutting edge must belong to the minimum spanning tree.
If the weight of an edge is the smallest of all the edges through a cut, it is called a light edge through the cut.
Theorem: let graph G=(V, E) be an undirected connected graph, and define A weighted function w with real value on E. Let A be A subset of e contained in A minimum spanning tree of G. If the cut (S, V-S) is any cut of G that does not destroy A, and the edge (u, v) is A light edge through the cut (S, V-S), then the edge (u, v) is safe for set A.
Corollary: let graph G=(V, E) be an undirected connected graph, and define A weighted function w with real value on E. Let A be A subset of E and contained in A minimum spanning tree of G. Let C=(Vc, Ec) be A connected component (tree) of forest Ga=(V, A). If edge (u, v) is A light edge connecting C and some other connected components in Ga, then edge (u, v) is safe for set A.
Kruskal algorithm and Prim algorithm
Kruskal algorithm and Prim algorithm are the refinements of the general algorithm, which determine the security edge by specific methods. In Krushal's algorithm, set A is A deep forest, and the security edge in set A is always the least weight edge connecting two different connected components in the graph. In Prim algorithm, set A is A tree. The security edge of set A always connects the minimum weight edge of A vertex that is not in the number.
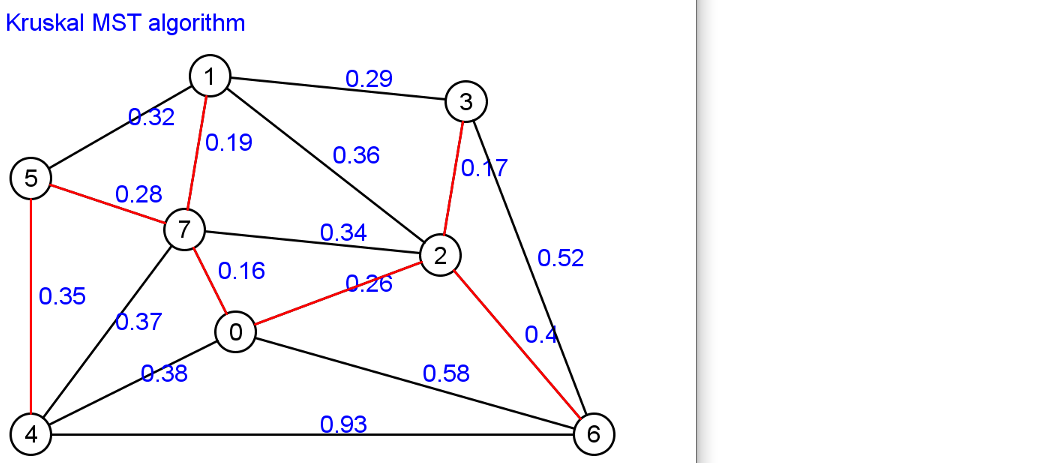
1. Kruskal algorithm
Set A is A forest, and the security edge in set A is always the least weight edge connecting two different connected components in the graph.
The way to find the secure edge of Kruskal algorithm is to find the edge with the least weight (u, v) in the edge of two different trees in all connected forests. Let C1 and C2 be the two trees connected by the edge (u, v). Since edge (u, v) must be a lightweight edge connecting C1 and some other tree, edge (u, v) is a safe edge of C1.
Implementation of Kruskal algorithm
In the implementation of Kruskal, a disjoint set data structure is used to maintain several disjoint sets of elements. Each set represents a tree in the current forest. Operation FindSet(u) returns a representative element in the containing element U set. By testing whether FindSet(u) is equal to FindSet(v), we can determine whether vertex u and v belong to the same tree. Union(u, v) is used to merge the two trees.

package mymst;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdDraw;
import edu.princeton.cs.algs4.StdOut;
import myutil.*;
public class MyKruskalMST {
private MyQueue<MyEdge> mst;
public MyKruskalMST(MyEWGraph G) {
mst = new MyQueue<MyEdge>();
MyPQ<MyEdge> pq = new MyPQ<MyEdge>();
for (MyEdge e : G.edges()) {
pq.insert(e);
}
MyUF uf = new MyUF(G.V());
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
MyEdge e = pq.delMin();
int v = e.either();
int w = e.other(v);
if (uf.find(v) != uf.find(w)) {
uf.union(v, w);
mst.enqueue(e);
}
}
}
public Iterable<MyEdge> edges() {
return mst;
}
public double weight() {
double w = 0.0;
for (MyEdge e : mst) {
w += e.weight();
}
return w;
}
/****************************************************/
/* Drawing interface */
/****************************************************/
public MyKruskalMST(MyEWGraph G, boolean draw) {
mst = new MyQueue<MyEdge>();
MyPQ<MyEdge> pq = new MyPQ<MyEdge>();
for (MyEdge e : G.edges()) {
pq.insert(e);
}
MyUF uf = new MyUF(G.V());
while (!pq.isEmpty() && mst.size() < G.V() - 1) {
MyEdge e = pq.delMin();
int v = e.either();
int w = e.other(v);
if (uf.find(v) != uf.find(w)) {
uf.union(v, w);
mst.enqueue(e);
//StdDraw.pause(1000);
//MyEWGraph.drawPoint(G.getPoint(v), 0.03, StdDraw.ORANGE);
StdDraw.pause(1000);
MyDraw.drawLine(G.getPoint(v), G.getPoint(w), StdDraw.RED);
}
}
}
public static void main(String[] args) {
// In in = new In(args[0]);
In in = new In("tinyEWG.txt");
MyEWGraph G = new MyEWGraph(in, true);
StdDraw.textLeft(30, 250, "Kruskal MST algorithm");
MyKruskalMST mst = new MyKruskalMST(G, true);
for (MyEdge e : mst.edges()) {
StdOut.println(e);
}
StdOut.println(mst.weight());
}
}
Kruskal algorithm analysis
The running time of Kruskal algorithm on graph G=(V, E) depends on the implementation of disjoint sets.
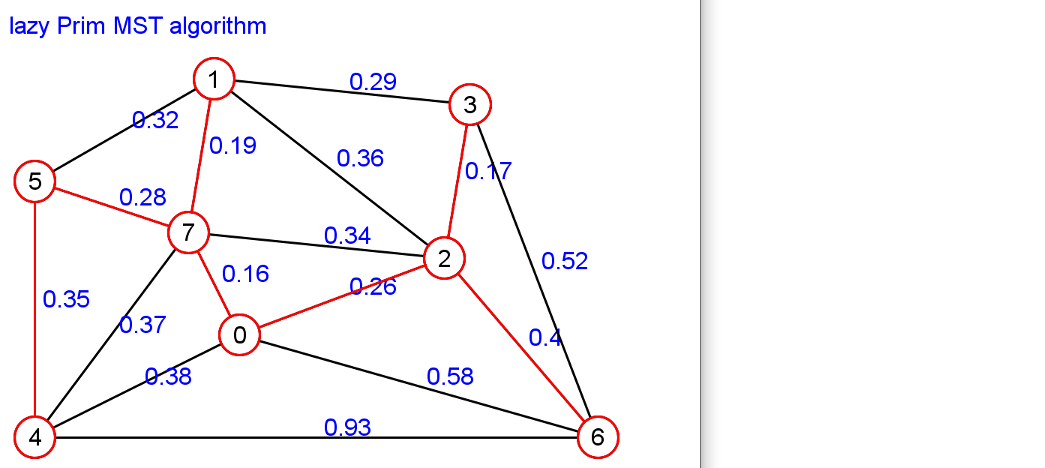
2. Prim algorithm
Set A is A tree, and adding the safety edge of set A always connects the minimum weight edge of the tree and A vertex that is not in the tree.
Prim algorithm implementation
The edges in set a always form a single tree, and the tree starts from any root vertex r, and gradually generates until the tree covers all the vertices in V. At each step, a light edge connecting an isolated vertex in tree A and G=(V, A) is added to tree a.
The key to the effective implementation of Prim algorithm is to find a new edge easily and add it to the tree formed by the edge of A.
package mymst;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdDraw;
import edu.princeton.cs.algs4.StdOut;
import myutil.*;
public class MyLazyPrimMST {
private boolean[] marked; // MST vertices
private MyQueue<MyEdge> mst; // MST edges
private MyPQ<MyEdge> pq; // crossing (and ineligible) edges
public MyLazyPrimMST(MyEWGraph G) {
pq = new MyPQ<MyEdge>();
marked = new boolean[G.V()];
mst = new MyQueue<MyEdge>();
prim(G, 0); // Prim's algorithm
}
private void prim(MyEWGraph G, int s) {
visit(G, s); // assumes G is connected
while (!pq.isEmpty()) {
MyEdge e = pq.delMin();
int v = e.either();
int w = e.other(v);
if (marked[v] && marked[w]) {
continue;
}
mst.enqueue(e); // add edge to tree
if (!marked[v]) {
visit(G, v);
}
if (!marked[w]) {
visit(G, w);
}
}
}
private void visit(MyEWGraph G, int v) {
marked[v] = true;
for (MyEdge e : G.adj(v)) {
if (!marked[e.other(v)]) {
pq.insert(e);
}
}
}
public Iterable<MyEdge> edges() {
return mst;
}
public double weight() {
double w = 0.0;
for (MyEdge e : edges()) {
w += e.weight();
}
return w;
}
/****************************************************/
/* Drawing interface */
/****************************************************/
private void visit(MyEWGraph G, int v, boolean draw) {
marked[v] = true;
StdDraw.pause(1000);
MyDraw.drawCircle(G.getPoint(v), MyDraw.CIRCLE_RADIUS, StdDraw.RED);
for (MyEdge e : G.adj(v)) {
if (!marked[e.other(v)]) {
pq.insert(e);
}
}
}
private void prim(MyEWGraph G, int s, boolean draw) {
visit(G, s, draw); // assumes G is connected
while (!pq.isEmpty()) {
MyEdge e = pq.delMin();
int v = e.either();
int w = e.other(v);
if (marked[v] && marked[w]) {
continue;
}
StdDraw.pause(1000);
MyDraw.drawLine(G.getPoint(v), G.getPoint(w), StdDraw.RED);
mst.enqueue(e); // add edge to tree
if (!marked[v]) {
visit(G, v, draw);
}
if (!marked[w]) {
visit(G, w, draw);
}
}
}
public MyLazyPrimMST(MyEWGraph G, boolean draw) {
pq = new MyPQ<MyEdge>();
marked = new boolean[G.V()];
mst = new MyQueue<MyEdge>();
prim(G, 0, draw);
}
public static void main(String[] args) {
// In in = new In(args[0]);
In in = new In("tinyEWG.txt");
MyEWGraph G = new MyEWGraph(in, true);
StdDraw.textLeft(30, 230, "lazy Prim MST algorithm");
MyLazyPrimMST mst = new MyLazyPrimMST(G, true);
for (MyEdge e : mst.edges()) {
StdOut.println(e);
}
StdOut.println(mst.weight());
}
}package mymst;
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdDraw;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.IndexMinPQ;
import myutil.*;
public class MyEagerPrimMST {
private MyEdge[] edgeTo;
private double[] distTo;
private boolean[] marked;
private IndexMinPQ<Double> pq;
public MyEagerPrimMST(MyEWGraph G) {
edgeTo = new MyEdge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++) {
distTo[v] = Double.POSITIVE_INFINITY;
}
pq = new IndexMinPQ<Double>(G.V());
prim(G, 0);
}
private void prim(MyEWGraph G, int s) {
distTo[s] = 0.0;
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin();
visit(G, v);
}
}
private void visit(MyEWGraph G, int v) {
marked[v] = true;
for (MyEdge e : G.adj(v)) {
int w = e.other(v);
if (marked[w]) { // v-w is ineligible
continue;
}
if (e.weight() < distTo[w]) {
edgeTo[w] = e;
distTo[w] = e.weight();
if (pq.contains(w)) {
pq.decreaseKey(w, distTo[w]);
} else {
pq.insert(w, distTo[w]);
}
}
}
}
public Iterable<MyEdge> edges() {
MyQueue<MyEdge> mst = new MyQueue<MyEdge>();
for (int v = 0; v < edgeTo.length; v++) {
MyEdge e = edgeTo[v];
if (e != null) {
mst.enqueue(e);
}
}
return mst;
}
public double weight() {
double w = 0;
for (MyEdge e : edges()) {
w += e.weight();
}
return w;
}
/****************************************************/
/* Drawing interface */
/****************************************************/
public MyEagerPrimMST(MyEWGraph G, boolean draw) {
edgeTo = new MyEdge[G.V()];
distTo = new double[G.V()];
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++) {
distTo[v] = Double.POSITIVE_INFINITY;
}
pq = new IndexMinPQ<Double>(G.V());
prim(G, 0, draw);
}
private void prim(MyEWGraph G, int s, boolean draw) {
distTo[s] = 0.0;
pq.insert(s, distTo[s]);
while (!pq.isEmpty()) {
int v = pq.delMin();
visit(G, v, draw);
}
}
private void visit(MyEWGraph G, int v, boolean draw) {
marked[v] = true;
StdDraw.pause(1000);
MyDraw.drawCircle(G.getPoint(v), MyDraw.CIRCLE_RADIUS, StdDraw.RED);
for (MyEdge e : G.adj(v)) {
int w = e.other(v);
if (marked[w]) { // v-w is ineligible
continue;
}
if (e.weight() < distTo[w]) {
edgeTo[w] = e;
distTo[w] = e.weight();
StdDraw.pause(1000);
MyDraw.drawLine(G.getPoint(v), G.getPoint(w), StdDraw.RED);
if (pq.contains(w)) {
pq.decreaseKey(w, distTo[w]);
} else {
pq.insert(w, distTo[w]);
}
}
}
}
public static void main(String[] args) {
// In in = new In(args[0]);
In in = new In("tinyEWG.txt");
MyEWGraph G = new MyEWGraph(in, true);
StdDraw.textLeft(30, 230, "eager Prim MST algorithm");
MyEagerPrimMST mst = new MyEagerPrimMST(G, true);
for (MyEdge e : mst.edges()) {
StdOut.println(e);
}
StdOut.println(mst.weight());
}
}
Prim algorithm analysis
The performance of Prim algorithm depends on the implementation of priority queue.
Properties of trees:
1. Connecting any two vertices in a tree with one edge will produce a new ring;
2. Deleting an edge from a tree will result in two independent trees.

