Write algorithm to judge whether an undirected graph is a tree.

[analysis]
The condition for a undirected graph G to be a tree is: G must be a connected graph without a loop or a connected graph with n-1 edges. Here we use the latter as the judging condition. For example, the following figure shows:

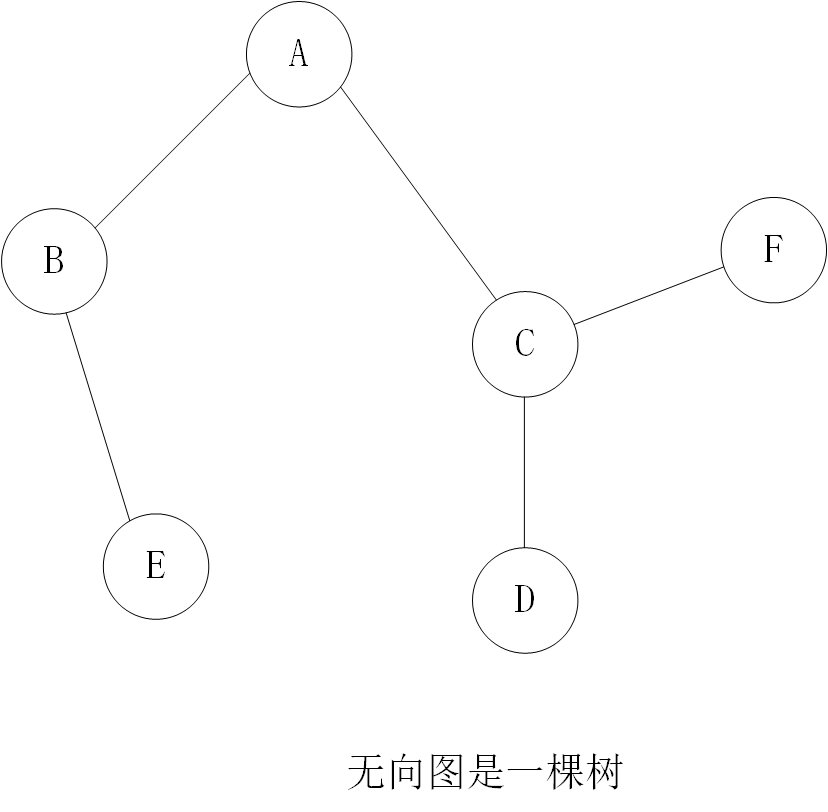
The undirected graph above is a tree with six vertices and five edges.

code:

#include<stdlib.h>
#include<stdio.h>
#include<malloc.h>
#include<string.h>
#include<iostream>
using namespace std;
/*Adjacency table type definition of Graphs*/
typedef char VertexType[4];
typedef char InfoPtr;
typedef int VRType;
#define MAXSIZE 100 / * maximum number of vertices*/
typedef enum { DG, DN, UG, UN }GraphKind; 	/*Types of graphs: directed graph, directed net, undirected graph and undirected net*/
typedef struct ArcNode			/*Type definition of edge node*/
{
	int adjvex; 				/*The position of the vertex pointed by the arc*/
	InfoPtr *info;				/*Arc related information*/
	struct ArcNode *nextarc; 	/*Indicates the next vertex adjacent to that vertex*/
}ArcNode;
typedef struct VNode			/*Type definition of head node*/
{
	VertexType data; 			/*Used to store vertices*/
	ArcNode *firstarc; 			/*Indicates the first vertex adjacent to the vertex*/
}VNode, AdjList[MAXSIZE];
typedef struct					/*Type definition of graph*/
{
	AdjList vertex;
	int vexnum, arcnum;			/*The number of vertices and arcs in a graph*/
	GraphKind kind; 			/*Types of Graphs*/
}AdjGraph;
int LocateVertex(AdjGraph G, VertexType v);
void CreateGraph(AdjGraph *G);
void DisplayGraph(AdjGraph G);
void DestroyGraph(AdjGraph *G);
void DFS(AdjGraph *G, int v, int *vNum, int *eNum, int visited[]);
int LocateVertex(AdjGraph G, VertexType v)
//Return to the corresponding position of vertices in the graph
{
	int i;
	for (i = 0; i < G.vexnum; i++)
		if (strcmp(G.vertex[i].data, v) == 0)
			return i;
	return -1;
}
void CreateGraph(AdjGraph *G)
//Using adjacency table storage structure to create undirected graph G
{
	int i, j, k;
	VertexType v1, v2;		//Define two vertices v1 and v2
	ArcNode *p;
	cout << "Please enter the number of vertices and edges of the graph: ";
	cin >> (*G).vexnum >> (*G).arcnum;
	cout << "Please input" << G->vexnum << "Value of vertices:" << endl;
	for (i = 0; i < G->vexnum; i++)	//Store vertex in head node
	{
		cin >> G->vertex[i].data;
		G->vertex[i].firstarc = NULL;	//Leave associated vertices empty
	}
	cout << "Please input the end of arc head:" << endl;
	for (k = 0; k < G->arcnum; k++)	//Set up side chain list
	{
		cin >> v1 >> v2;
		i = LocateVertex(*G, v1);/*Determine the number corresponding to v1*/
		j = LocateVertex(*G, v2);/*Determine the number corresponding to v2*/
								 //j creates an adjacency table for arc head i and arc tail
		p = (ArcNode*)malloc(sizeof(ArcNode));
		p->adjvex = j;
		p->info = NULL;
		p->nextarc = G->vertex[i].firstarc;
		G->vertex[i].firstarc = p;
		//i creates an adjacency table for arc head j and arc tail
		p = (ArcNode*)malloc(sizeof(ArcNode));
		p->adjvex = i;
		p->info = NULL;
		p->nextarc = G->vertex[j].firstarc;
		G->vertex[j].firstarc = p;
	}
	(*G).kind = UG;
}
void DestroyGraph(AdjGraph *G)
//Destroy undirected graph G
{
	int i;
	ArcNode *p, *q;
	for (i = 0; i < (*G).vexnum; i++)	//Release edge table node in graph
	{
		p = G->vertex[i].firstarc;//p points to the first node of the edge table
		if (p != NULL)			//If the edge table is not empty, the nodes of the edge table are released
		{
			q = p->nextarc;
			free(p);
			p = q;
		}
	}
	(*G).vexnum = 0;		//Set the number of vertices to 0
	(*G).arcnum = 0;		//Set the number of sides to 0
}
void DisplayGraph(AdjGraph G)
//Adjacency matrix G of output graph
{
	int i;
	ArcNode *p;
	cout << G.vexnum << "Apex:" << endl;
	for (i = 0; i < G.vexnum; i++)
		cout << G.vertex[i].data << " ";
	cout << endl << G.arcnum << "Strip edge:" << endl;
	for (i = 0; i < G.vexnum; i++)
	{
		p = G.vertex[i].firstarc;
		while (p)
		{
			cout << G.vertex[i].data << "→" << G.vertex[p->adjvex].data << " ";
			p = p->nextarc;
		}
		cout << endl;
	}
}
int IsTree(AdjGraph *G)
{
	int vNum = 0, eNum = 0, i, visited[MAXSIZE];
	for (i = 0; i < G->vexnum; i++)
		visited[i] = 0;
	DFS(G, 0, &vNum, &eNum, visited);
	if (vNum == G->vexnum && eNum == 2 * (G->vexnum - 1))
		return 1;
	else
		return 0;
}
void DFS(AdjGraph *G, int v, int *vNum, int *eNum, int visited[])
{
	ArcNode *p;
	visited[v] = 1;
	(*vNum)++;
	p = G->vertex[v].firstarc;
	while (p != NULL)
	{
		(*eNum)++;
		if (visited[p->adjvex] == 0)
			DFS(G, p->adjvex, vNum, eNum, visited);
		p = p->nextarc;
	}
}
void main()
{
	AdjGraph G;
	cout << "Using adjacency table to create undirected graph G: " << endl;
	CreateGraph(&G);
	cout << "Output undirected graph G Adjacency table of:" << endl;
	DisplayGraph(G);
	if (IsTree(&G))
		cout << "Undirected graph G It's a tree.!" << endl;
	else
		cout << "Undirected graph G Not a tree!" << endl;
	DestroyGraph(&G);

	system("pause");
}

Result:

Use adjacency table to create undirected graph G:
Please enter the number of vertices and edges of the graph: 6 5
 Enter values for 6 vertices:
A B C D E F
 Please enter the tail arc head:
A B
A C
B E
C D
C F
 Output adjacency table of undirected graph G:
6 vertices:
A B C D E F
 The 5 side:
A→C A→B
B→E B→A
C→F C→D C→A
D→C
E→B
F→C
 Undirected graph G is a tree!