In ACM competitions, we often encounter various power-seeking problems, which usually correspond to a large number of numbers, so fast power will often be used, fast power is very useful, even if the principle of fast power is not clear, as long as there are templates, it can be solved quickly.

First of all, we will talk about some important formulas:
Modular arithmetic is similar to the basic four arithmetic operations, with the exception of division. Its rules are as follows:

(a + b) % p = (a % p + b % p) % p (1) // This formula will be used in the next title.
(a – b) % p = (a % p – b % p) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
(a^b) % p = ((a % p)^b) % p (4) //The Formula of Fast Power

Associative law:

((a+b) % p + c) % p = (a + (b+c) % p) % p (5)
((a*b) % p * c)% p = (a * (b*c) % p) % p (6)

Commutative law:

(a + b) % p = (b+a) % p (7)
(a * b) % p = (b * a) % p (8)

Distributive law:

((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p (9)

Important Theorems:

Start with the most commonly used templates:
1. Fast Multiplication: a*b

int qmul(int a,int b){// long long can be selected according to the data range 
    int ans=0;
    while(b){
        if( b&1)ans+=a;//Judgment of Bit and Completion Number 1
        b>>=1;a<<=1;//Bit Operations Replace/2 and*2
    }
    return ans;
}

2. Fast Multiplication Modulation (a*b)%mod

int qmul_mod(int a,int b,int mod){
    int ans=0;
    while(b){
        if((b%=mod)&1)ans+=a%=mod;//Here we need b%=mod and a%=mod 
        b>>=1;a<<=1;
    }
    return ans%mod;  //ans also needs to model mod 
}

3. Fast power a^b

int qpow(int a,int b){
    if(a==0)return 0;//This is a pit. The school competition has been pitted. Many online implementations have not written this point.
    int ans=1;
    while(b){
        if(b&1)ans*=a;//The difference between fast multiplication and fast multiplication
        b>>=1;a*=a;//Difference, ibid.
    }
    return ans;
}

4. Fast power modulus (a^b)%mod

int qpow_mod(int a,int b,int mod){
    if(a==0)return 0;
    int ans=1;
    while(b){
        if(b&1)ans=(ans%mod)*(a%mod);//If you are sure that the data will not explode, it can be written as ans*=a%=mod.
        b>>=1;a*=a%=mod;//Equivalent to a=(a%mod)*(a%mod), and a modular operation is replaced by assignment, which improves efficiency.
    }
    return ans%mod;//If the data doesn't explode, the% operation here will be equivalent to the repeated ans%mod in the fifth section.
}

Example POJ 1995
I just pulled it over on VJ without linking it.
Topic Meaning:
There's a game where everyone can have two numbers Ai and Bi.
Now you have to figure out the Ai^Bi of all the people and add them all up to output the mod results.
That's: (A1^B1+A2^B2+A3^B3 +.................................................................................................................................................................. An^Bn)%mod;
Output the result of the formula above will allow the data range to be less quickly powered over.
But here we use the formulas mentioned earlier.

// POJ 1995
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long ll;
ll qpow_mod(ll a,ll b,ll mod){
    if(a==0) return 0;
    ll ans = 1;
    while(b){
      if(b&1) ans = (ans%mod)*(a%mod);
      b>>=1;
      a*=a%=mod;
    }
    return ans%mod;
}
int main(int argc, char const *argv[])
{
    int T;
    int m,n;
    ll sum;
    //freopen("input.txt","r",stdin);
    //freopen("output.txt","w",stdout);
    scanf("%d",&T);
    while(T--){
        sum = 0;
        scanf("%d",&m);
        scanf("%d",&n);
        for(int i=0;i<n;i++){
            int a,b;
            scanf("%d %d",&a,&b);
            sum = sum + qpow_mod(a,b,m);
        }
        printf("%lld\n",sum%m);
    }
    return 0;
}

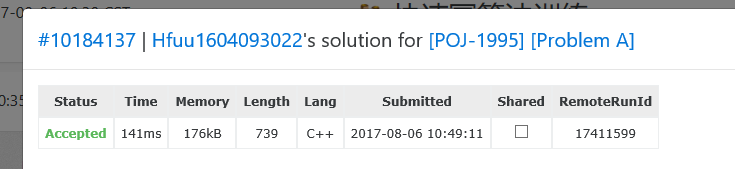
It's awkward to use 141ms. It's not particularly fast, but it's not slow, at least Ac.
That's all for fast power.
And then I think it's a competition after all. I think it's normal to prepare templates.
And when my strength is not particularly strong now, I think it is advisable to prepare some templates. Although I can not fully understand this template, I know a little bit about it, and then I will use it slowly to understand the essence of the algorithm myself in the process of using it slowly.
The team Team 090 of Tsinghua University played three AK matches four times in the previous Hangzhou TV multi-university League matches. One difficult problem was that they did not come out with A. They were admired very much. There was a big gap between them and Dashen. We can learn from them, at least better than yesterday's team.