Portal

Topic: The preface of the K dictionary to satisfy the topic meaning. (The AAB and AAC are the same in the title meaning, so there will be no AAC.

Solution: If you draw it by yourself, you will have the following graph (just take the problem directly), and you can find that the acceptable range of sons under a node is the largest letter + 1 on the path to that node, such as the third letter A on the bottom layer of the graph. Consider that the sons it can receive are A, B and C.

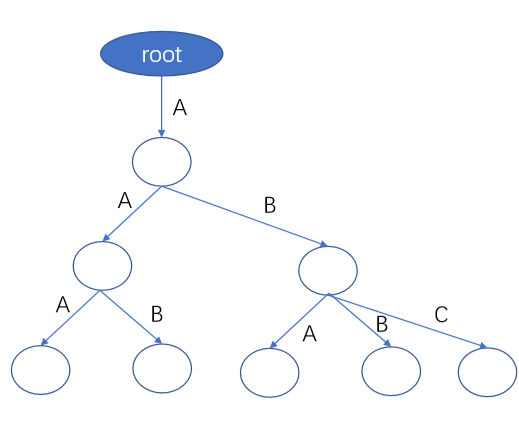
If we can know the number of different dictionary orders that each of its sons can represent at a given node, then this problem can be solved.

Let dp[i][j]: denote the number of Lexicographic orders with the largest number of I bits ahead and the largest number of J bits behind.

The equation of state transition is dp[i][j]=i*dp[i][j-1]+dp[i+1][j-1]; because when I is the highest position in front of us now, we can consider that the son that can be placed in the jth position is the same as i, dp[i][j-1]; and the other one is that i+1 is placed in the jth position. There is also the use of _int 128 to explode ll.

#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int N=35;
template <typename _Tp> il void read(_Tp&x) {
	char ch;bool flag=0;x=0;
	while(ch=getchar(),!isdigit(ch)) if(ch=='-')flag=1;
	while(isdigit(ch)) x=x*10+ch-'0',ch=getchar();
	if(flag) x=-x;
}
template <typename _Tp> il void print(_Tp&x) {
	if(x<0) {x=-x;putchar('-');}
	if(x>9) print(x/10);
	putchar(x%10+'0');
}
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
__int128 dp[N][N],k;//dp[i][j]: The largest number of schemes before and after I is the number of schemes with J bits 
int n,T;
char s[N];
il void init(){
	dp[26][1]=26,dp[26][0]=1;
	for(int i=1;i<=25;++i) dp[i][0]=1,dp[i][1]=i+1;
	for(int j=2;j<=26;++j){
		for(int i=25;i>=1;--i){
			dp[i][j]=(__int128)i*dp[i][j-1]+dp[i+1][j-1];
		}
	}
//	cout<<"init over"<<endl;
//	for(int i=1;i<=3;++i){
//		for(int j=1;j<=3;++j) print(dp[i][j]),cout<<" ";
//		cout<<endl;
//	}
} 
int main() {
	init();
	read(T);
	for(int t=1; t<=T; ++t) {
		read(n),read(k);
		int mx=1;
		for(int i=1;i<=n;++i){
			s[i]='A';
			for(int j=1;j<=26;++j){
				mx=max(mx,j);
				if(k<=dp[mx][n-i]){
					s[i]='A'-1+j;
					break;
				}
				k-=dp[mx][n-i];
			}
		}
		printf("Case #%d: ",t);
		for(int i=1;i<=n;++i) printf("%c",s[i]);
		printf("\n");
	}
	return 0;
}