Preface

In computational geometry, we often need to find the extreme point of a 2D Polygon. For example, through the extreme point of x\y, we can define the bounding box of a polygon. More generally, we may need to find the extreme point of a polygon in any direction. For the point set of n points, it is easy to find an O(n) algorithm, just test each point in turn. However, for convex polygons, we can use the idea of binary search in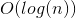Find the extreme point in time. First, we define an arbitrary direction vector u, and then we explain the idea of the algorithm in detail.

The convex hull of plane point set and simple polygon has been introduced in these two articles: Convex hull algorithm of plane point set,Polygon fast convex hull algorithm . Therefore, for the plane point set and any simple polygon, we only need to calculate the convex hull first, and then calculate the convex hull extreme point. The complexity of the algorithm is determined by the convex hull algorithm.

Algorithm of convex hull extremum

First of all, it is defined that 2D convex polygon S is composed of n points V0,V1,...,Vn-1,Vn=V0, and is given in a counterclockwise direction.

Definition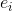Is the i-th edge (from Vi to Vi+1),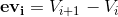Is the edge vector.

Objective: to find the extreme points of all points in S in u direction. That is to say, the point is projected on the line defined by u theory, and the extreme point is the extreme point of the projection point, as shown in the following figure:

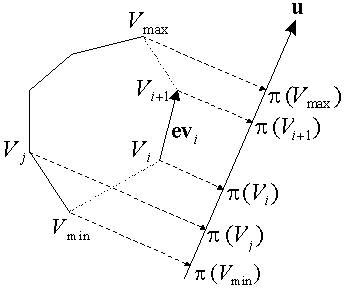
As you can see, VIS is above Vj relative to u. That is, a sharp angle is formed between (Vi Vj) and u, which is equivalent to the following geometric conditions:

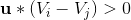
This condition can help us judge one side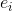Is the projection increasing or decreasing relative to u.

Violence algorithm

The most direct way is to search each point violently, and compare each step with the currently saved extreme point. The pseudo code of the algorithm is as follows:

Input: W = {V0,V1,...,Vn-1}  n Point set of points
       u = Given direction vector
//Mark max = min = 0.
for each point Vi in {V1,...,Vn-1}  (i=1,n-1)
{
    if (u · (Vi - Vmax) > 0) {  // Viis above the prior max
        max = i;                // new max index = i
        continue;               // a new max can't be a new min
    }
    if (u · (Vi - Vmin) < 0)    // Vi is below the prior min
        min = i;                // new min index = i
}

return max = Of maximum point Index
       min = Of the minimum point Index

Although the algorithm is linear, it can also be accelerated by binary search.

Two point search

For the point set of a convex polygon, we can use binary search to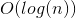Find the extreme point in time.

First of all, suppose that the maximum point is between the vertex Va and Vb, and Vc is the middle point between Va and Vb. In order to achieve binary search, we need to narrow the next search scope to [a, c] or [c, b]. Since the polygon is convex, we can compare the edge vectors at A and C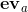,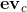To do that. Details are as follows:

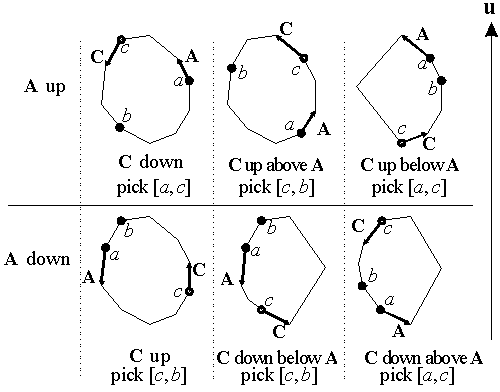
As shown above. If u is upward, there may be six relative positions of A, B and C. For each case, either [a, c], or [c, b] contains the maximum point. This is because polygon S is monotonic in the U direction. It consists of two monotonic chains, starting from the minimum value point, increasing monotonically to the maximum value point, and then decreasing monotonically back to the minimum value point. And whatever the direction of u, this conclusion is true.

Next, we can construct a binary search. from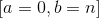At first,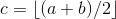At each step, we need to determine whether to increase a to c or decrease b to c, and reduce the interval containing the maximum value by half. Of course, we need to check whether a local maximum point Vc has been found, which only needs to be checke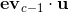dand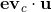Whether the symbols of are consistent is enough. If the symbols of the two are not the same, Vc is the local maximum point and the global maximum point of the polygon.

Therefore, we get the pseudo code to find the maximum value point relative to u as follows:

Input: OMEGA = {V0,V1,...,Vn-1,Vn=V0} is a 2D proper convex polygon
       u = a 2D direction vector

if V0 is a local maximum, then return 0;
Put a=0; b=n;
Put A = the edge vector at V0;
forever {
    Put c = the midpoint of [a,b] = int((a+b)/2);
    if Vc is a local maximum, then it is the global maximum
        return c;

    // no max yet, so continue with the binary search
    // pick one of the two subchains [a,c] or [c,b]
    Put C = the edge vector at Vc;
    if (A points up) {
        if (C points down) {
            b = c;                     select [a,c]
        }
        else C points up {
            if Va is above Vc {
                 b = c;                 select [a,c]
            }
            else Va is below Vc {
                 a = c;                 select [c,b]
                 A = C;
            }
        }
    }
    else A points down {
        if (C points up) {
            a = c;                     select [c,b]
            A = C;
        }
        else C points down {
            if Va is below Vc {
                 b = c;                 select [a,c]
            }
            else Va is above Vc {
                 a = c;                 select [c,b]
                 A = C;
            }
        }
    }
    if (b <= a+1) then the chain is impossibly small
        return an error; since something's  wrong
}

Here is a C + + implementation of the binary search algorithm:

// Assume that classes are already given for the objects:
//    Point and Vector (2D) with:
//        coordinates {float x, y;}
//        operators for:
//            == to test equality
//            != to test inequality
//            =  for assignment
//            -Vector for unary minus
//            Point  = Point ± Vector
//            Vector = Point - Point
//            Vector = Vector ± Vector
//    Line with defining points {Point P0, P1;}
//===================================================================


// dot product (2D) which allows vector operations in arguments
#define dot(u,v)   ((u).x * (v).x + (u).y * (v).y)

// tests for vector orientation relative to a direction vector u
#define up(u,v)         (dot(u,v) > 0)
#define down(u,v)       (dot(u,v) < 0)
#define dr(u,Vi,Vj)     (dot(u, (Vi)-(Vj))) // direction sign of (Vi-Vj)
#define above(u,Vi,Vj)  (dr(u,Vi,Vj) > 0)   // true if Vi is above Vj
#define below(u,Vi,Vj)  (dr(u,Vi,Vj) < 0)   // true if Vi is below Vj
 

// polyMax_2D(): find a polygon's max vertex in a specified direction
//    Input:  U   = a 2D direction vector
//            V[] = array vertices of a proper convex polygon
//            n   = number of polygon vertices, with V[n]=V[0]
//    Return: index (>=0) of the maximum vertex, or
//            (-1) = an error [Note: should be impossible, but...]
int
polyMax_2D( Vector U, Point* V, int n )
{
    if (n < 10) {               // use brute force search for small polygons
        int max = 0;
        for (int i=1; i<n; i++)     // for each point in {V1,...,Vn-1}
            if (above(U, V[i], V[max]))  // if V[i] is above prior V[max]
                 max = i;                // new max index = i
        return max;
    }

    // use binary search for large polygons
    int     a, b, c;            // indices for edge chain endpoints
    Vector  A, C;               // edge vectors at V[a] and V[c]
    int     upA, upC;           // test for "up" direction of A and C

    a=0; b=n;                   // start chain = [0,n] with V[n]=V[0]
    A = V[1] - V[0];
    upA = up(U,A);
    // test if V[0] is a local maximum
    if (!upA && !above(U, V[n-1], V[0]))    //  V[0] is the maximum
        return 0;

    for(;;) {
        c = (a + b) / 2;        // midpoint of [a,b], and 0<c<n
        C = V[c+1] - V[c];
        upC = up(U,C);
        if (!upC && !above(U, V[c-1], V[c])) // V[c] is a local maximum
            return c;                        // thus it is the maximum

        // no max yet, so continue with the  binary search
        // pick one of the two subchains [a,c]  or [c,b]
        if (upA) {                       // A points up
            if (!upC) {                      // C points down
                 b = c;                       // select [a,c]
            }
            else {                           // C points up
                 if (above(U, V[a], V[c])) {    // V[a] above V[c]
                     b = c;                       // select [a,c]
                 }
                 else {                         // V[a] below V[c]
                     a = c;                       // select [c,b]
                     A = C;
                     upA = upC;
                 }
            }
        }
        else {                           // A points down
            if (upC) {                       // C points up
                 a = c;                       // select [c,b]
                 A = C;
                 upA = upC;
            }
            else {                           // C points down
                 if (below(U, V[a], V[c])) {    // V[a] below V[c]
                     b = c;                       // select [a,c]
                 }
                 else {                         // V[a] above V[c]
                     a = c;                       // select [c,b]
                     A = C;
                     upA = upC;
                 }
            }
        }
        // have a new (reduced) chain [a,b]
        if (b <= a+1)           // the chain is impossibly small
            return (-1);        // return an error: something's wrong
    }
}
//===================================================================