catalogue
1, The concept of heap and the creation of heap
2, Construction of heap method
3, Use of priority queue (heap) method
3.1 heap initialization (creation of large heap and small heap)
5, Find and minimum K-pair numbers
1, The concept of heap and the creation of heap
1. Concept of heap
What is a pile? (logically, the heap is a complete binary tree, which is actually stored in an array)
We store a complete binary tree into an array through sequence traversal, which is called heap.
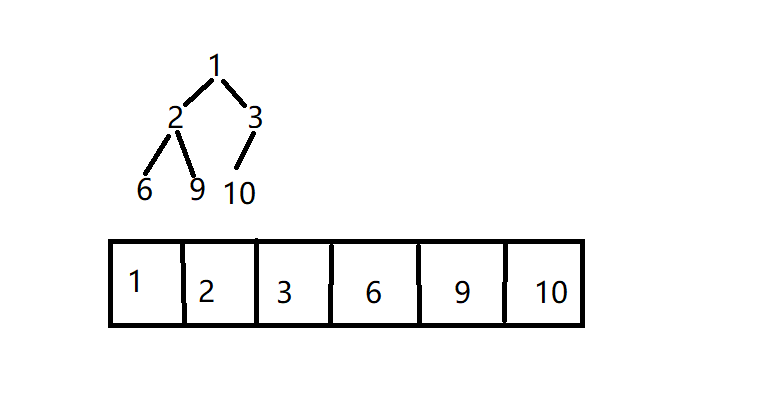
Note: the element in the heap cannot be empty. (waste a lot of space)
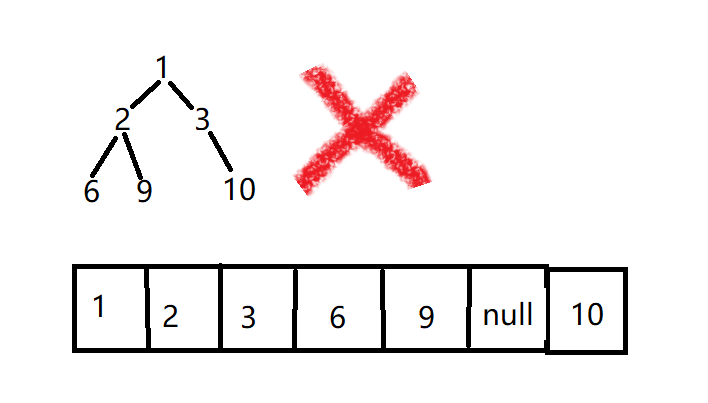
What are big root piles and small root piles?
Large root heap: the value of all nodes is greater than the value of their child nodes, which is called large root heap.
Small root heap: the value of all nodes is less than the value of their child nodes, which is called small root heap.
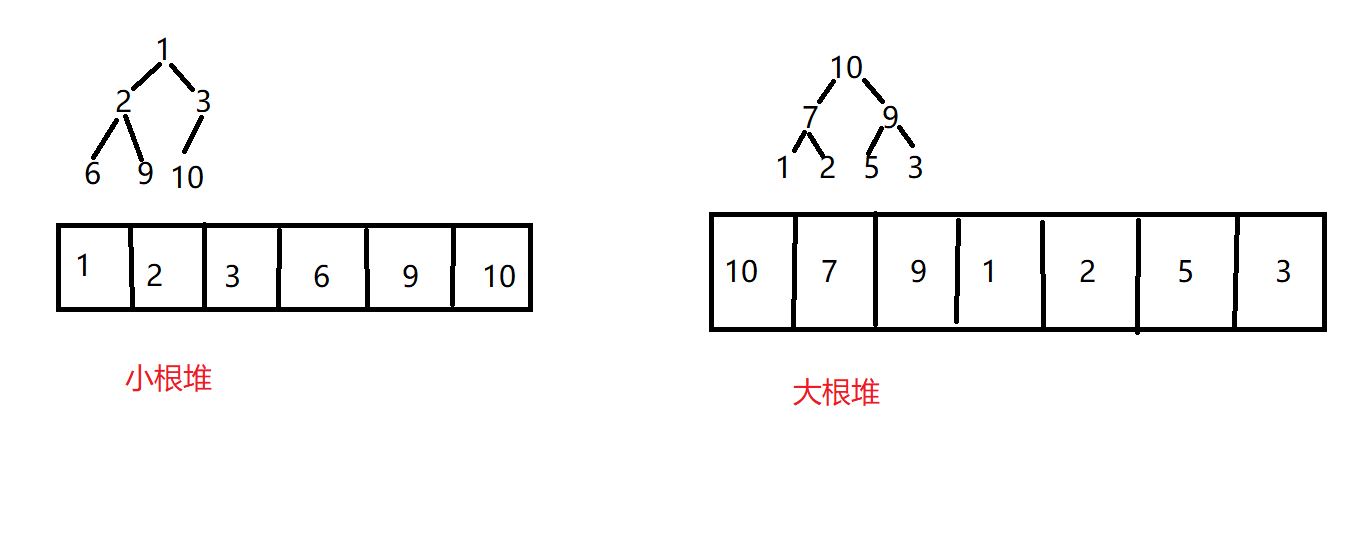
Note: when the parent node is i, the left child's node is i*2+1 and the right child's node is i*2+2;
When the child node is I, the father node is (i-1) / 2;
2. Heap creation
2.1 downward traversal
For the sorting in the heap, we can use the downward traversal method. Let's take the downward traversal of a small heap as an example.
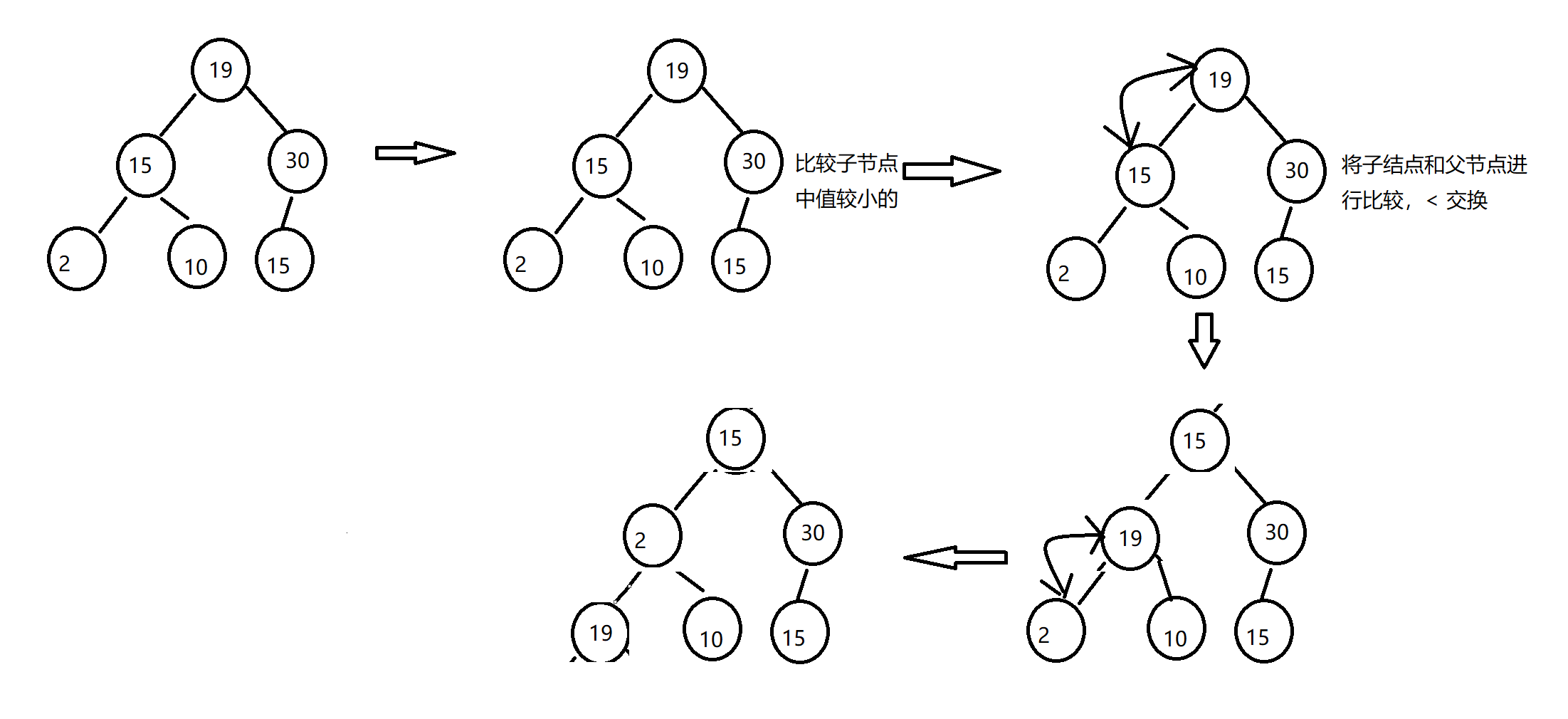
2.2 reactor building operation
Since the bottom of the heap is an array, we start by creating an array and initializing it.
public class TestHeap {
public int[] elem;
public int uesdSize;
public TestHeap(){
this.elem=new int[10];
}
}Next, we will put an unordered array into it and copy it through the elem array. At the same time, we will continue to traverse the top-down functions from bottom to top.
public void createBigHeap(int[] array){
for(int i=0;i<array.length;i++){
this.elem[i]=array[i];
this.usedSize++;
}
for(int i=(this.usedSize-1-1)/2;i>=0;i--){
shiftDown(i);
}
}Next, we write the up-down function shiftDown(i);
public void shiftDown(int parent){
int child=parent*2+1;
while (child<this.usedSize){
if(child+1<this.usedSize && this.elem[child+1]<this.elem[child]){
child++;
}
if(this.elem[parent]>this.elem[child]){
int temp=this.elem[parent];
this.elem[child]=this.elem[parent];
this.elem[parent]=temp;
parent=child;
child=child*2+1;
}else {
break;
}
}
}Note: Generally speaking, the time complexity of the for loop is N, and the time complexity of the shiftDown loop is logN, so it is O(N*logN), but it is actually O(N);

2, Construction of heap method
2.1 queue entry
For the queue operation, we use the method of upward traversal.
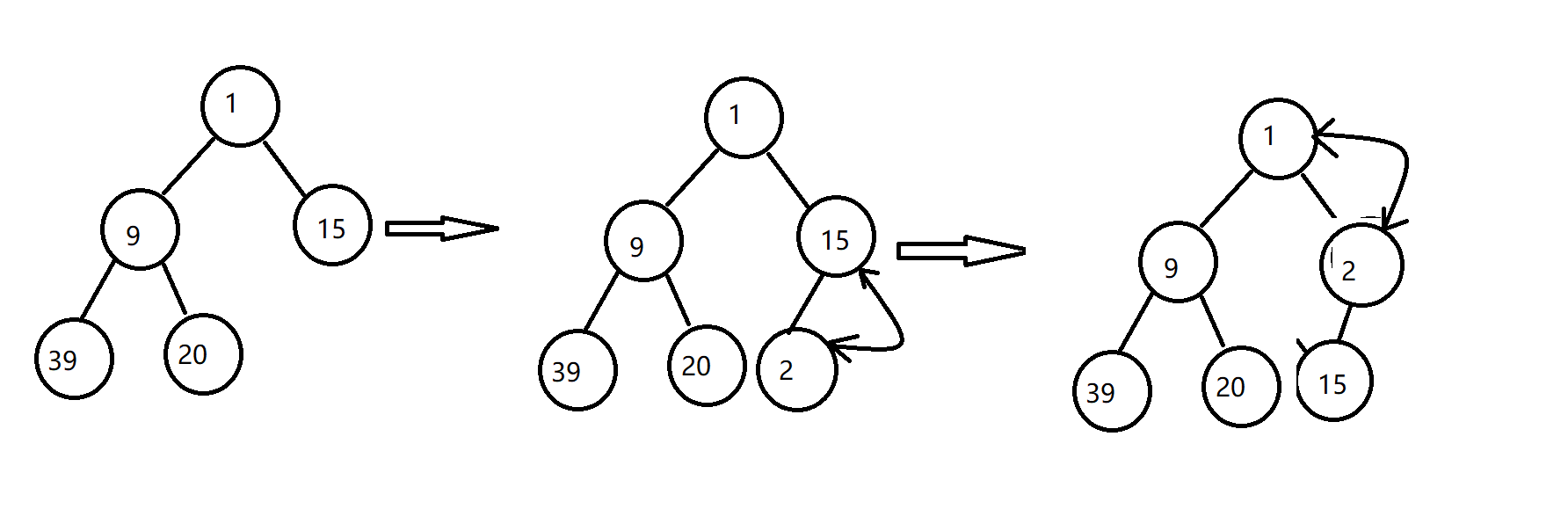
When entering the queue, we first judge whether it is full, then we put the value in the queue into the last one of the array, compare it with its parent node, and exchange if it is less than 0 until the parent node is less than 0;
public boolean isFull(){
return this.elem.length==this.usedSize;
}
public void push(int val){
if(isFull()){
this.elem=Arrays.copyOf(this.elem,2*this.elem.length);
}
this.elem[this.usedSize]=val;
this.usedSize++;
shiftUp(this.usedSize-1);
}
public void shiftUp(int child){
int parent=(child-1)/2;
while (parent>=0){
if(this.elem[parent]>this.elem[child]){
int temp=this.elem[parent];
this.elem[parent]=this.elem[child];
this.elem[child]=temp;
child=parent;
parent=(parent-1)/2;
}else{
break;
}
}
}2.2 out of queue operation
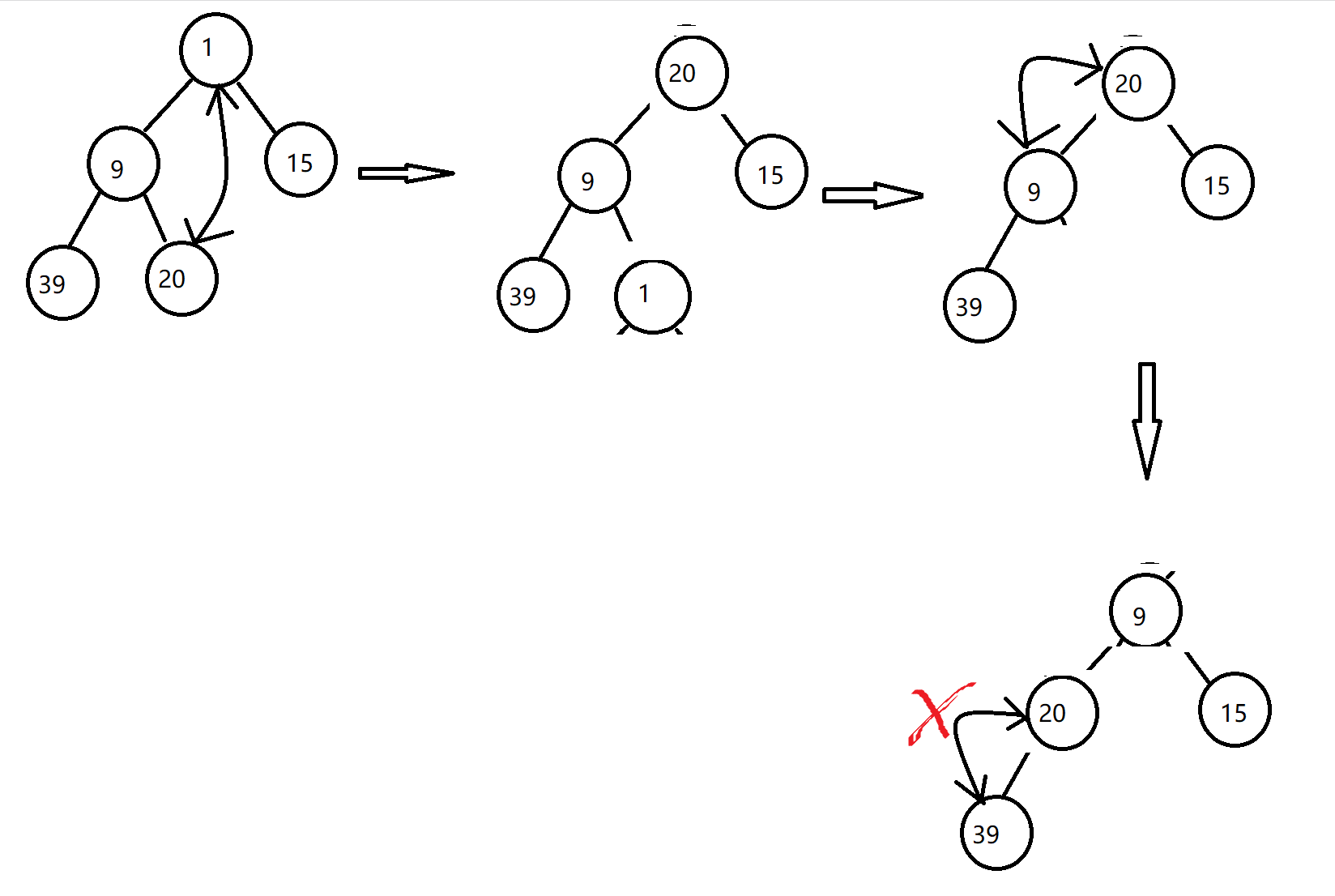
For the out of queue operation, we first exchange the head and tail, and then traverse the head down.
public int pop(){
if(isEmpty()){
throw new RuntimeException("It is empty and cannot be taken out");
}
int temp=this.elem[0];
this.elem[0]=this.elem[this.usedSize-1];
this.elem[this.usedSize-1]=temp;
this.usedSize--;
shiftDown(0);
return temp;
}
public boolean isEmpty(){
return this.usedSize==0;
}2.3 viewing header elements
Similar to the out of queue operation, there is no need to exchange and remove.
public boolean isEmpty(){
return this.usedSize==0;
}
public int peek(){
if(isEmpty()){
throw new RuntimeException("It is empty and cannot be taken out");
}
return this.elem[0];
}3, Use of priority queue (heap) method
PriorityQueue is the priority queue
The following is its method and use:

public static void main(String[] args) {
PriorityQueue<Integer> pq=new PriorityQueue<>();
pq.offer(1);
pq.offer(2);
pq.offer(3);
System.out.println(pq.poll());
System.out.println(pq.poll());
System.out.println(pq.poll());
//1 2 3
}We can see that PriorityQueue is a small heap when used.
3.1 heap initialization (creation of large heap and small heap)
For the creation of large and small heaps, we need to override the Comparator method to operate.
We use anonymous inner classes to write. The detailed methods are as follows:
Small pile:
PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1-o2;
}
});Pile:
PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});We can also abbreviate it as: (we can use it in doing questions)
Small pile:
PrioritQueue<Integer> pq=new PriorityQueue<>((x,y) -> (x-y));
Pile:
PriorityQueue<Integer> pq=new PriorityQueue<>((x,y) -> (y-x));
4, Heap sort (heap)
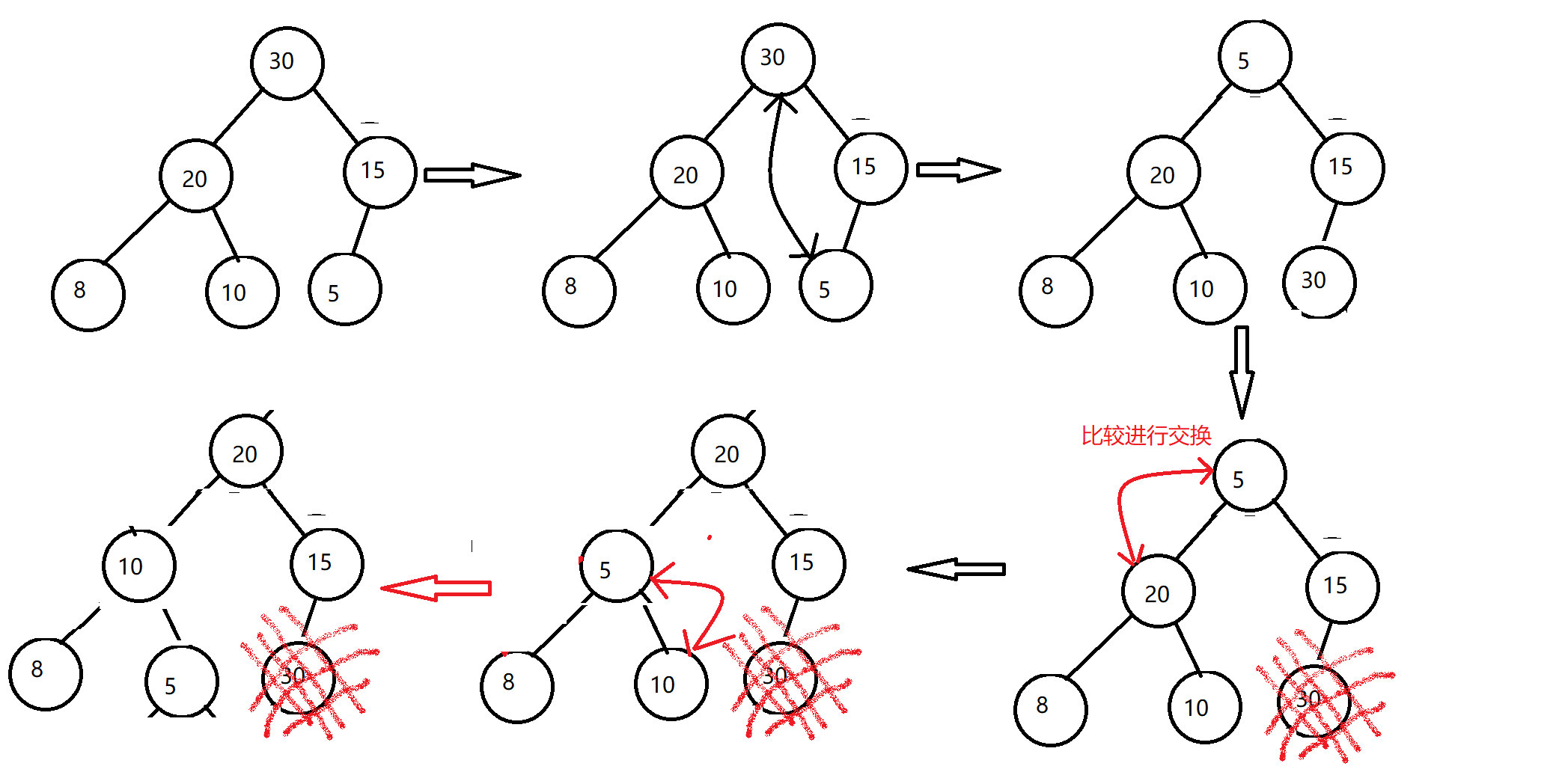
We first turn the array into a large number, and then exchange the first number with the last number. At this time, the largest number is determined. Fix the number, sort the first number, and repeat the above process.
Code implementation:
//Heap sort
public void heapSory(){
int end=this.usedSize-1;
while (end>0){
int temp=this.elem[0];
this.elem[0]=this.elem[end];
this.elem[end]=temp;
shiftDown01(0,end);
end--;
}
}
public void shiftDown01(int parent,int k){
int child=parent*2+1;
while (child<k){
if(child+1<k && this.elem[child+1]>this.elem[child]){
child++;
}
if(this.elem[child]>this.elem[parent]){
int temp=this.elem[child];
this.elem[child]=this.elem[parent];
this.elem[parent]=temp;
parent=child;
child=child*2+1;
}else{
break;
}
}
}5, Find and minimum K-pair numbers
Buckle link: Title Link.
5.1 using small heap
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
class Data{
public int val01;
public int val02;
public Data(int val01,int val02){
this.val01=val01;
this.val02=val02;
}
public int get01(){
return this.val01;
}
public int get02(){
return this.val02;
}
}
public class Test01 {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<List<Integer>> list=new ArrayList<>();
PriorityQueue<Data> pq=new PriorityQueue<>(new Comparator<Data>() {
@Override
public int compare(Data o1, Data o2) { //Small pile
return (o1.get01()+o1.get02())-(o2.get01()+o2.get02());
}
});
for(int i=0;i<Math.min(nums1.length,k);i++){
for(int j=0;j<Math.min(nums2.length,k);j++){
pq.offer(new Data(nums1[i],nums2[j]));
}
}
int n=Math.min(pq.size(),k);
for(int i=0;i<n;i++){
List<Integer> list1=new ArrayList<>();
Data temp=pq.poll();
list1.add(temp.get01());
list1.add(temp.get02());
list.add(list1);
}
return list;
}
}5.2 realization by using
public class Test03 {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<List<Integer>> pq=new PriorityQueue<>
(new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));//Heaps
}
});
for(int i=0;i<Math.min(nums1.length,k);i++){
for(int j=0;j<Math.min(nums2.length,k);j++){
if(pq.size()<k){
List<Integer> list=new ArrayList<>();
list.add(nums1[i]);
list.add(nums2[j]);
pq.offer(list);
}else{
int temp=pq.peek().get(0)+pq.peek().get(1);
if(temp>nums1[i]+nums2[j]){
pq.poll();
List<Integer> list=new ArrayList<>();
list.add(nums1[i]);
list.add(nums2[j]);
pq.offer(list);
}
}
}
}
List<List<Integer>> lists=new ArrayList<>();
for(int i=0;i<k && !pq.isEmpty();i++){
lists.add(pq.poll());
}
return lists;
}
}Note: to judge some critical conditions, be sure to pay attention.