1. Calculate the following integrals with the trapezoidal method of variable step size to make the accuracy reach 10-4.

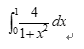
Requirement:

(1) the information of the accuracy ε and the end points a and b of the interval are input from the keyboard terminal;

(2) print out the calculation results of each step.

Source code:
#include<iostream>
#include<cmath>
using namespace std;
int main(){
	double x,a,s,b,e,h,T1,T2;
	cout<<"Please enter the range endpoint a,b And precision e:"<<endl; 
	cin>>a>>b>>e;
	cout<<endl;
	h = b-a;
	T1 = (h/2)*(4/(1+pow(a,2))+4/(1+(pow(b,2))));
	int count=0;
	cout<<"K    "<<"  T1   "<<"     T2  "<<endl;
	do{
		if(count!=0){
			h  = h/2;
			T1 = T2;
		}
		count++;
		s = 0;
		x = a + h/2;
		do{
			s = s + (4/(1+pow(x,2)));
			x = x + h;
		}while(x<b);
		T2 = (T1/2)+h*s/2;
		printf("%d:  %.6lf   %.6lf\n",count,T1,T2); 
	}while(abs(T2-T1)>=e);
	cout<<endl;
	printf("The final results are as follows:%.4lf",T2);
	return 0;
}

2. Calculate the following integral values with the longberg algorithm to achieve the accuracy of 10-4.

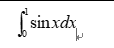
Requirement:

(1) draw the implementation block diagram of longberg algorithm;

(2) the information of the accuracy ε and the end points a and b of the interval are input from the keyboard terminal;

(3) print out the calculation results of trapezoid sequence, Simpson sequence, Cotes sequence and longberg sequence according to the calculation sequence of longberg algorithm, as shown below;

(4) output the integration approximate value that meets the accuracy requirements finally.

Algorithm block diagram

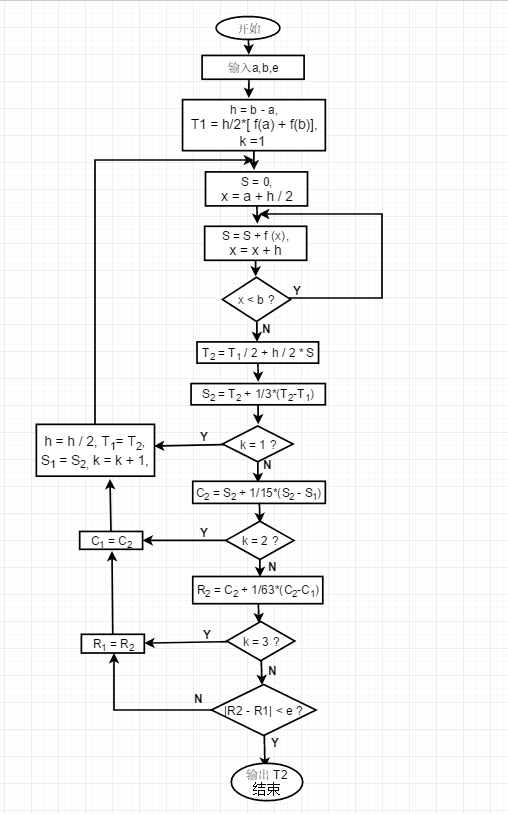
#include<iostream>
#include<cmath>
using namespace std;
int main(){
	double x,a,s,b,e,h,T1,T2;
	cin>>a>>b>>e;
	double q[7][7];
	double T[100] = {0}; 
	h = b-a;
	int d=0;
	int i,j;
	for(i=0;i<7;i++){
		for(j=0;j<7;j++){
			if(j == 0){
				q[i][j] = pow(2,i);
			}
			else{
				q[i][j] = 0;
			}
		}
	}
    T1 = (h/2)*(sin(b)+sin(a));
	int count=-1,k=0;
	do{
		if(count!=-1){
			h  = h/2;
			T1 = T2;
		}
		count = pow(2,k);
		k++;
		s = 0;
		x = a + h/2;
		do{
          s = s + sin(x);
			x = x + h;
		}while(x<b);
		T2 = (T1/2)+h*s/2;
		T[count] = T1;
		q[d++][1] =  T[count];
	}while(abs(T2-T1)>=e);
	cout<<endl;
	double S[100] = {0};
	double C[100] = {0};
	double R[100] = {0};
	d = 1;
	for(int i=1;i<=count/2;i=i*2){
		S[i] = (4.00/3)*T[2*i]-(1.00/3)*T[i];
		q[d++][2] = S[i];
	}
	cout<<endl;
	d = 2;
	for(int i=1;i<=count/4;i=i*2){
		C[i] = (16.00/15)*S[2*i]-(1.00/15)*S[i];
		q[d++][3] = C[i];
	}
	cout<<endl;
	d = 3;
	for(int i=1;i<=count/8;i=i*2){
		R[i] = (64.00/63)*C[2*i]-(1.00/63)*C[i];
		q[d++][4] = R[i];
	}
	cout<<"n"<<"   Trapezoidal sequence  "<<"  Simpson sequence  "<<" Cortez sequence  "<<"  Longberg sequence "<<endl; 
	for(i=0;i<6;i++){
		for(j=0;j<5;j++){
			if(q[i][j] == 0){
				printf("     ");
			}
			else{
				if(j==0){
					printf("%.0lf ",q[i][j]);
					if(q[i][j]<=8) printf(" ");
				}
				else{
					printf("%.8lf   ",q[i][j]);
				}
			}
		}
		printf("\n");
	}
	printf("\n The final results are as follows: %.4lf",q[3][4]); 
	return 0;
}