Topic connection:
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=6003

Title:

Abstract: array a obtains array b by exchanging a pair of numbers, and gives the following two values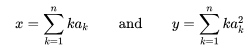
Ask how many switching methods are possible to satisfy the condition. The values of x and y may not match the array. In this case, output 0

Train of thought:
Find out X1 and Y1 of the array after swapping, (y1-y) / (x1-x) is the sum of the two numbers of swapping
If, (y1-y) and (x1-x) are not multiples, the proof is mismatched
If, (x1-x) = = 0, it is proved that two identical numbers are exchanged. If y1 and y are not equal, it is proved that they are mismatched
If y1 and y are equal, then they are matched. At this time, only how many pairs of the same number need to be found

In advance, an aj = (y1-y) / (x1-x) - a [i]
x2-x = (B [j] - B [i]) * (j-I), assuming j is larger than I
If b[j] - b[i] is 0, continue;
We can find out how much j is by the above formula, and then check whether the B [j] of this position is equal to the pre calculated aj

Code:

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
#define ll long long
const int MAX=1e5+10;
map <ll,ll> m;
ll a[MAX];
ll b[MAX];

int main()
{
   int t,n;
   ll x,y,x1,y1,ans;
   scanf("%d",&t);
   while(t--){
     m.clear();
     x1=0,y1=0,ans=0;
     scanf("%d%lld%lld",&n,&x,&y);
     for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
        b[i] = a[i] * a[i];
        m[a[i]]++;
     }
     for(int i=1;i<=n;i++){
        x1 = x1 + i*a[i];
        y1 = y1 + i*b[i];
     }
     if(x == x1){
        if(y1 != y){
            puts("0");
            continue;
        }
        else{
            map <ll,ll>::iterator it;
            for(it = m.begin();it != m.end();it++){
                ll num = it->second;
                ans = ans + num*(num-1)/2;
            }
            printf("%lld\n",ans);
            continue;
        }
     }
     ll x2 = abs(x1-x);
     ll y2 = abs(y1-y);
     if( y2 % x2 != 0){
        puts("0");
        continue;
     }

     ll dy = y1-y;
     ll dx = x1-x;
     ll tmp = dy/dx;
     for(int i=1;i<=n;i++){
        ll aj = tmp - a[i];
        ll dt = aj-a[i];
        if(dt == 0)
            continue;
        ll jj=(dx+dt*i)/dt;
        if(jj <= i || jj > n )
            continue;
        if(a[jj] == aj)
            ans++;
     }
     printf("%lld\n",ans);
   }
   return 0;
}