Direct insert sort

Dynamic diagram demonstration:

Basic idea:

Insert the records to be sorted into an ordered sequence one by one according to the size of their key values, until all records are inserted into the sequence
A new ordered sequence is obtained.

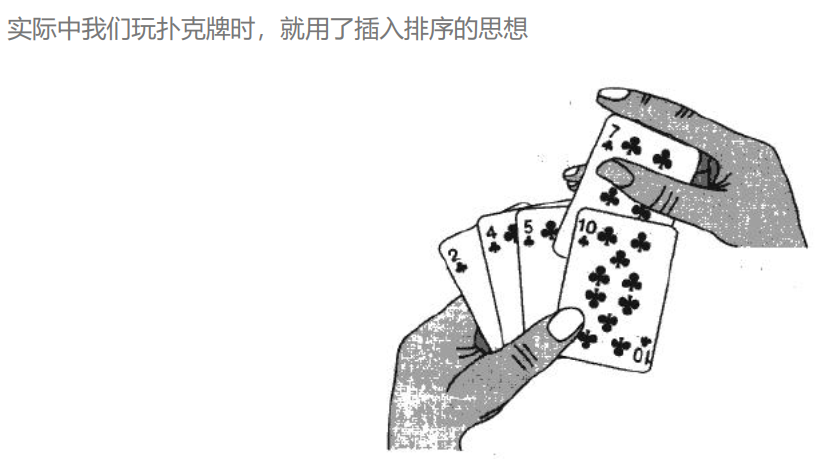
Code implementation:

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;// Records the subscript of the last element of an ordered sequence
		int tmp = a[end + 1];// Record the data to insert
		while (end >= 0)
		{
			// Looking for data smaller than tmp
			if (a[end]>tmp)
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}		
		}
		// Insert tmp after or in the first place of data smaller than tmp
		a[end + 1] = tmp;
	}
}

Summary of characteristics of direct insertion sort:

1. The closer the element set is to order, the higher the time efficiency of the direct insertion sorting algorithm
2. Time complexity: O(N^2)
3. Spatial complexity: O(1), which is a stable sorting algorithm
4. Stability: stable

Stability: it is assumed that there are multiple records with the same keyword in the record sequence to be sorted. If sorted, the relative order of these records will be lower
The order remains unchanged, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], while in the sorted sequence, r[i] is still before r[j]
The order algorithm is stable; Otherwise, it is called unstable.

Shell Sort

Dynamic diagram demonstration:

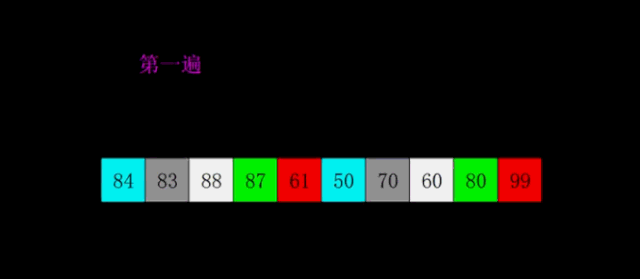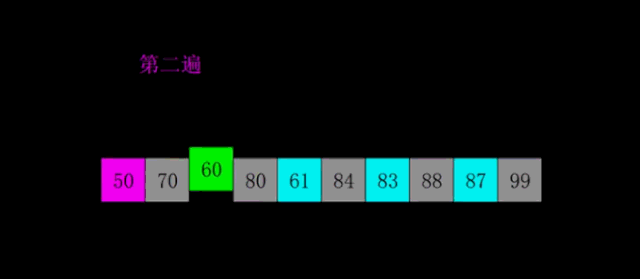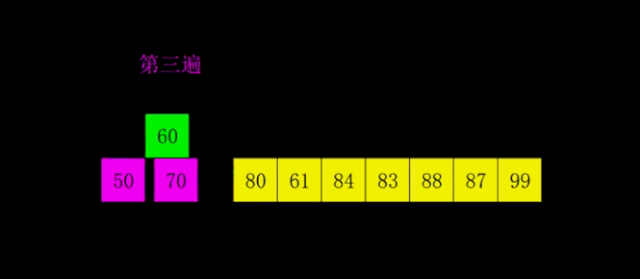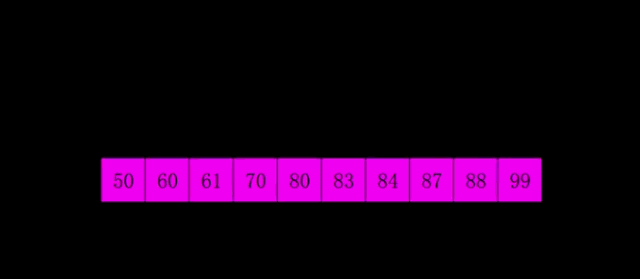
Basic idea:

First, select a gap less than N, divide all records in the file to be sorted into groups, divide all elements with gap distance into the same group, and sort the records in each group. Then assign the value of gap/3+1 to gap and repeat the above grouping and sorting. When arrival = 1, all records are arranged in a unified group.

Shilling gap is equal to 5. At this time, the elements with a distance of 5 are divided into a group, and each group is directly inserted and sorted

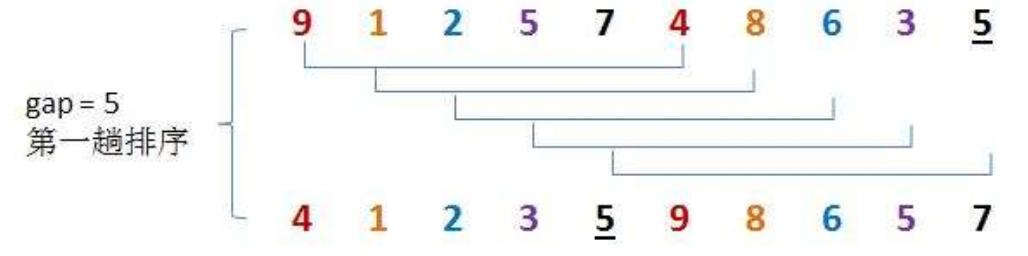
Then let gap=gap/3+1=2. At this time, the elements with a distance of 2 are divided into a group, and each group is inserted and sorted

Then perform the above operations. At this time, gap is 1, all data are divided into a group, and the group of data is inserted and sorted

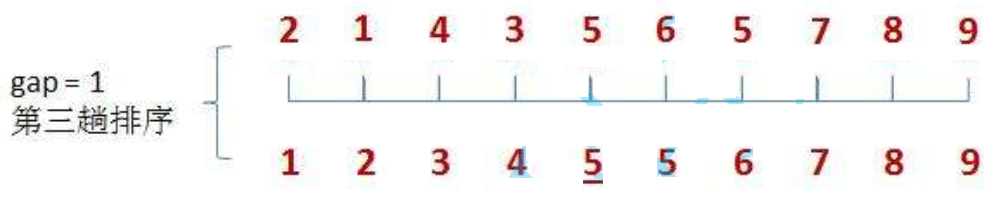
Code implementation:

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;// Reduce the number of sorting groups
		// Direct sort
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

Summary of Hill sort characteristics:

1. Hill sort is an optimization of direct insertion sort
2. When gap > 1, the array is pre sorted in order to make the array closer to order. When gap == 1, the array is close to ordered, which will be very fast
3. Through a large number of test statistics, the time complexity is about O (N^1.3)
4. Stability: unstable

Direct selection sort

Dynamic diagram demonstration:

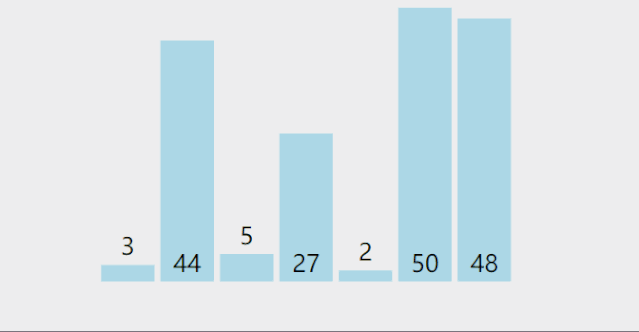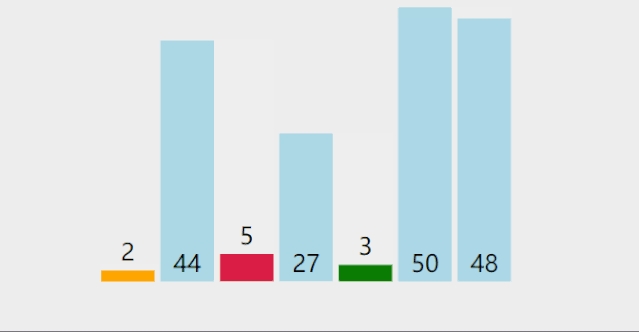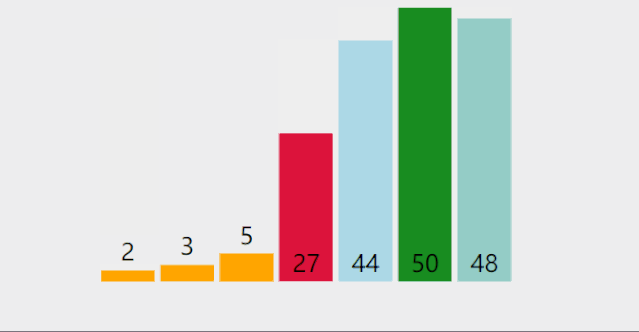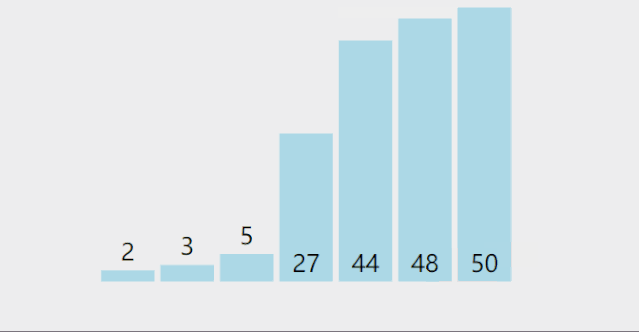
Basic idea:

1. Select the largest (smallest) data element in the element set
2. If it is not the last (first) element in the group, it is exchanged with the last (first) element in the group
3. In the remaining set, repeat the above steps until there is 1 element left in the set

Code implementation:

void SelectSort2(int* a, int n)
{
	int i = 0,j=0;	
	for (i = 0; i < n-1; i++)
	{
		int min = i;// Take out the subscript of the first element
		// Find the subscript of the minimum value
		for (j = i + 1; j < n; j++)
		{
			if (a[j]<min)
			{
				min = j;
			}
		}
		Swap(&a[min], &a[i]);
	}
}

In order to improve efficiency, we can traverse to find the maximum and minimum values at one time

code:

void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		// Record the maximum and minimum coordinates
		int min = begin, max = end;
		// Find the coordinates of the maximum and minimum values
		for (int i = begin; i < end; i++)
		{
			if (a[min]>a[i])
				min = i;

			if (a[max] < a[i])
				max = i;
		}
		Swap(&a[begin], &a[min]);
		// Prevent the maximum value from being at the beginning of the sequence and being exchanged by the minimum value
		if (max == begin)
		{
			max = min;
		}
		Swap(&a[end], &a[max]);
		begin++;
		end--;
	}
}

Summary of characteristics of direct selection sorting:

1. It is very easy to understand the direct selection sorting thinking, but the efficiency is not very good. Rarely used in practice
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: unstable

Heap sort

Dynamic diagram demonstration:

Basic idea:

To use heap sorting, first build a heap. Note that a large heap needs to be built in descending order and a small heap needs to be built in ascending order

How to build a reactor?
Find the last non leaf node and carry out the following operations from the back to the front: (take jiandui as an example here) take the incoming node as the parent node, compare its two child nodes, compare the child node with the parent node, exchange if it is larger than the parent node, and take the position of the original child node as the parent node, and repeat the above operations. If the parent node is larger than the child node, the operation ends.

The code is as follows:

// Downward adjustment
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n&&a[child] < a[child + 1])
		{
			child++;
		}

		if (a[child]>a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void test()
{
	// Adjusted from the last non leaf node.
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a,n,i);
	}
}

After the heap is built, we will sort it (taking ascending order as an example). Here we will help you understand it in the way of illustration and text

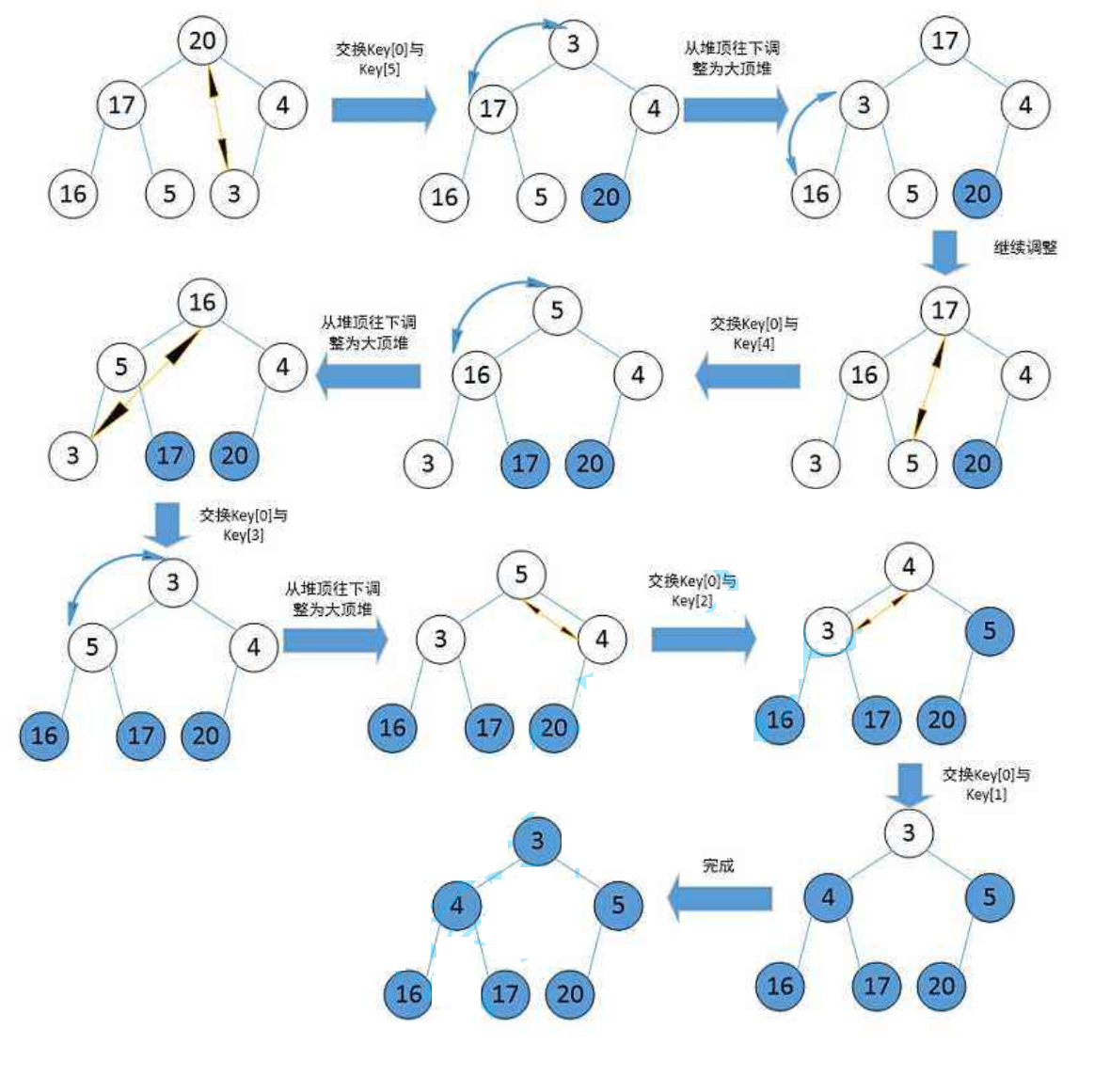
Code implementation:

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;// Find child node
	while (child < n)
	{
		// Find the larger value in the child node
		if (child + 1 < n&&a[child] < a[child + 1])
		{
			child++;
		}

		if (a[child]>a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	// Find the last non leaf node and adjust it from front to back.
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a,n,i);
	}

	int end = n - 1;
	// sort
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

Summary of characteristics of heap sorting:

1. Heap sorting uses heap to select numbers, which is much more efficient
2. Time complexity: O(N*logN)
3. Space complexity: O(1)
4. Stability: unstable

Bubble sorting

Dynamic diagram demonstration:

Basic idea:

Two adjacent elements are compared, and if they are different, they are exchanged until the last element

Code implementation:

void BubbleSort(int* a, int n)
{
	for (int end = n; end > 0; --end)
	{
		int exchange = 1;
		//A bubble sort, with the maximum at the end
		for (int i = 1; i < end; i++)
		{
			if (a[i - 1]>a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 0;
			}
		}
		//Exit without exchange in a bubble sort
		if (exchange)
			break;
	}
}

Summary of bubble sorting characteristics:

1. Bubble sort is a sort that is very easy to understand
2. Time complexity: O(N^2)
3. Space complexity: O(1)
4. Stability: stable

Count sort

Basic idea:

Counting sorting is not sorting by comparing the size of data, but by counting the number of the same elements in the array, and then returning the elements to the original array in order.

When the elements in the arr array are large, starting from zero will cause a great waste of space. For example, the array elements are 101103, 104106, and we can't open up 106 spaces. In order to get rid of the above situation, we need to use mapping: first traverse the array to find the minimum min and maximum max, and map the [min,max] range to the range [0, max min + 1].

Code implementation:

void CountSort(int* a, int n)
{
	int min = a[0];
	int max = a[0];
	//Select the maximum and minimum values in the array
	for (int i = 1; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];

		if (a[i]>max)
			max = a[i];
	}

	int range = max - min + 1;
	int* count = (int*)calloc(range, sizeof(int));

	//Statistical times
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	//sort
	int i = 0;
	for (int j = 0; j < range; j++)
	{
		while (count[j]--)
		{
			a[i++] = j + min;
		}
	}
}

Quick row

hoare version

Dynamic diagram demonstration of one operation:

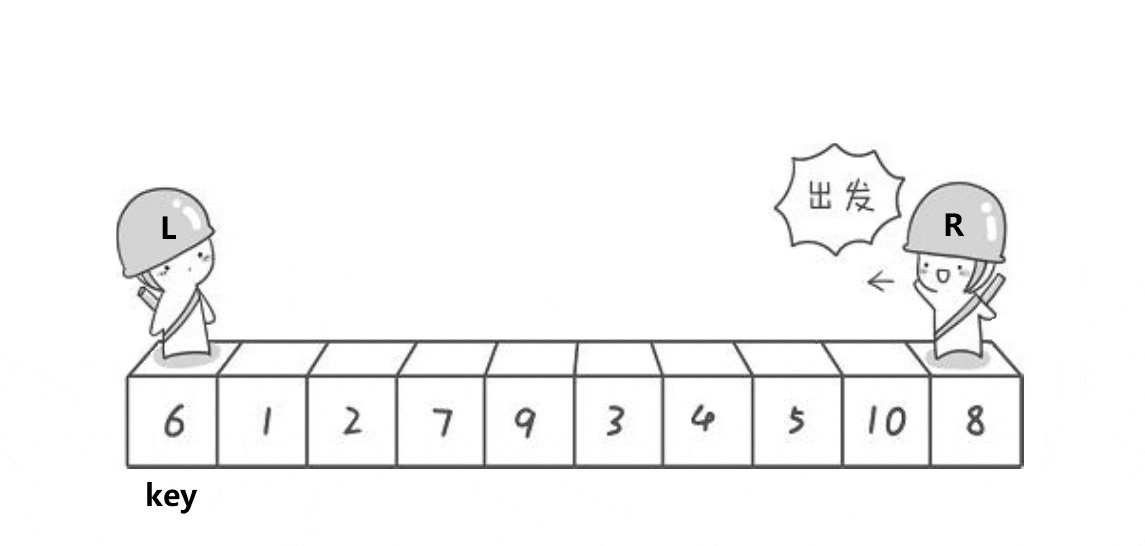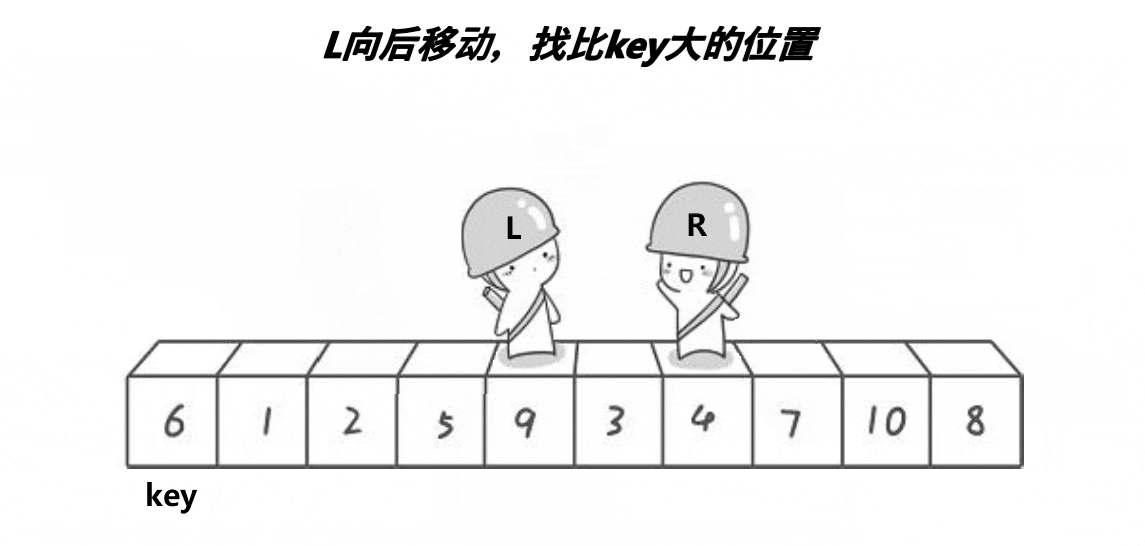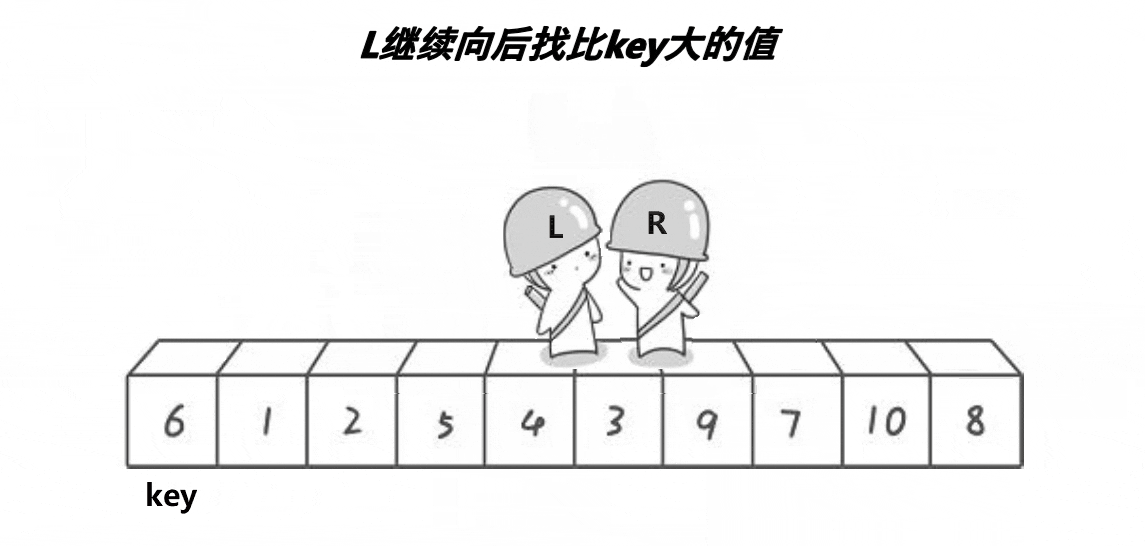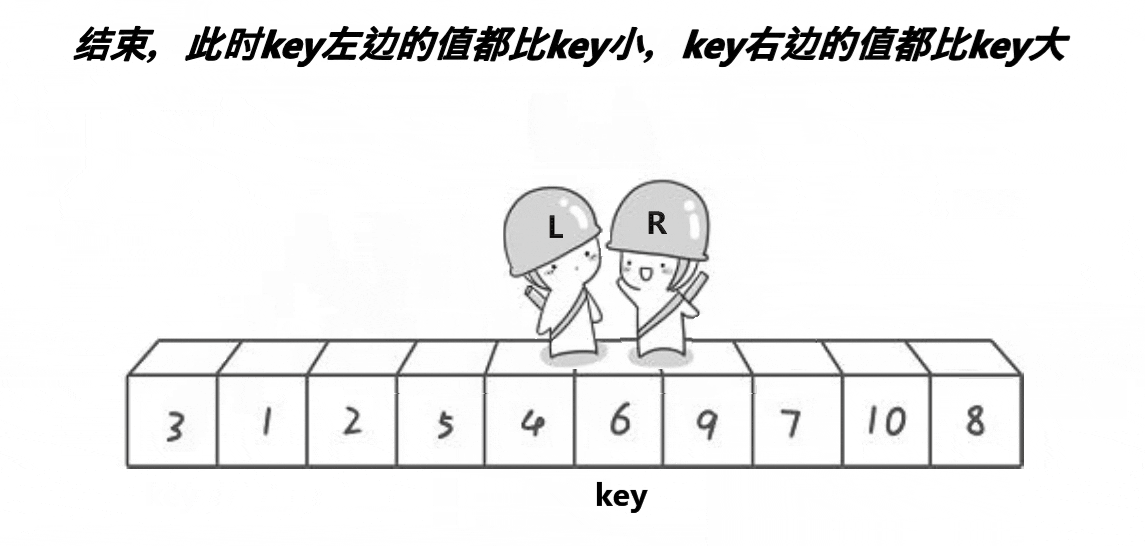
Basic idea:

1. Select a key first (usually the leftmost)
2. Then create left and right to represent the first data and the last data of the array respectively
3. Let right go ahead first. When right finds data smaller than the key, left starts to go back. When left finds data larger than the key, left stops, exchanges the data of right and left, and then repeats the previous operation until left and right meet, and then exchanges the key and left.
4. After the previous steps, the key is preceded by smaller elements and followed by larger elements. At this time, the operation is performed on the left and right sides of the key respectively, and recursion continues until there is only one data in the left and right sequences, or the left and right sequences do not exist

Code implementation:

int PartSort(int* a, int left, int right)
{
	int keyi = left;
	while (left < right)
	{
		//The left side is smaller than keyi
		while (left<right&&a[right]>a[keyi])
		{
			right--;
		}
		//Look for keyi on the right
		while (left < right&&a[left] < a[keyi])
		{
			left++;
		}
		//Swap size found
		Swap(&a[right], &a[left]);
	}
	Swap(&a[left], &a[keyi]);

	return left;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = PartSort(a, left, right);
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

Excavation method

Dynamic diagram demonstration of one operation:

Basic idea:

1. Take out a data key (usually the first) as the pit position
2. Create left and right to represent the first data and the last data of the array respectively
3. Let right go ahead first. When right finds data smaller than the key, take out the data and put it into the original pit to form a new pit. Then let left go back. When left finds data larger than the key, take out the data and put it into the pit formed by right to form a new pit. Until left and right meet, fill the data key into the final pit
4. key, perform this operation on the left and right sides respectively, and recurse until there is only one data in the left and right sequences, or the left and right sequences do not exist to complete the sorting

int PartSort(int* a, int left, int right)
{
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		//Find a small hole on the right, fill the hole and form a new hole by yourself
		while (left<right&&a[right]>key)
		{
			right--;
		}
		a[hole] = a[right];
		hole = right;
		//Find a big hole on the left, fill the hole and form a new hole by yourself
		while (left < right&&a[left] < key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[hole] = key;
	return hole;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = PartSort(a, left, right);
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

Front and back pointer method

Dynamic diagram demonstration of one operation:

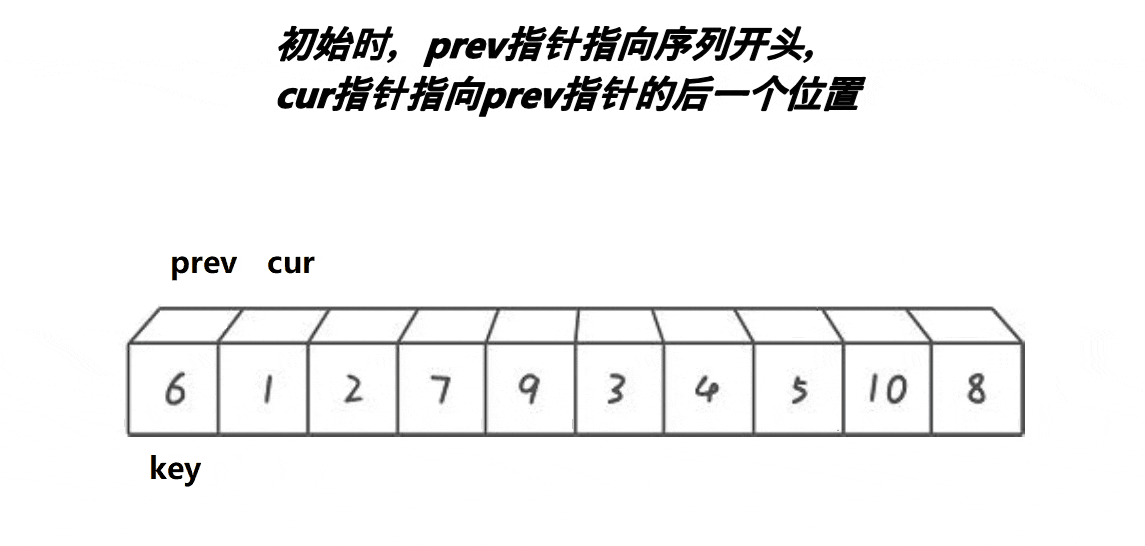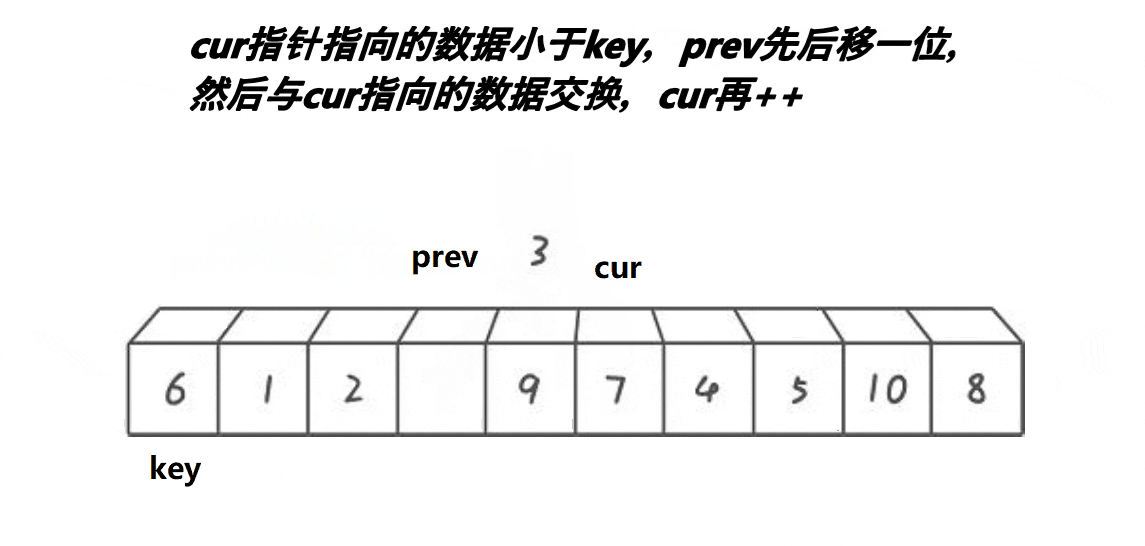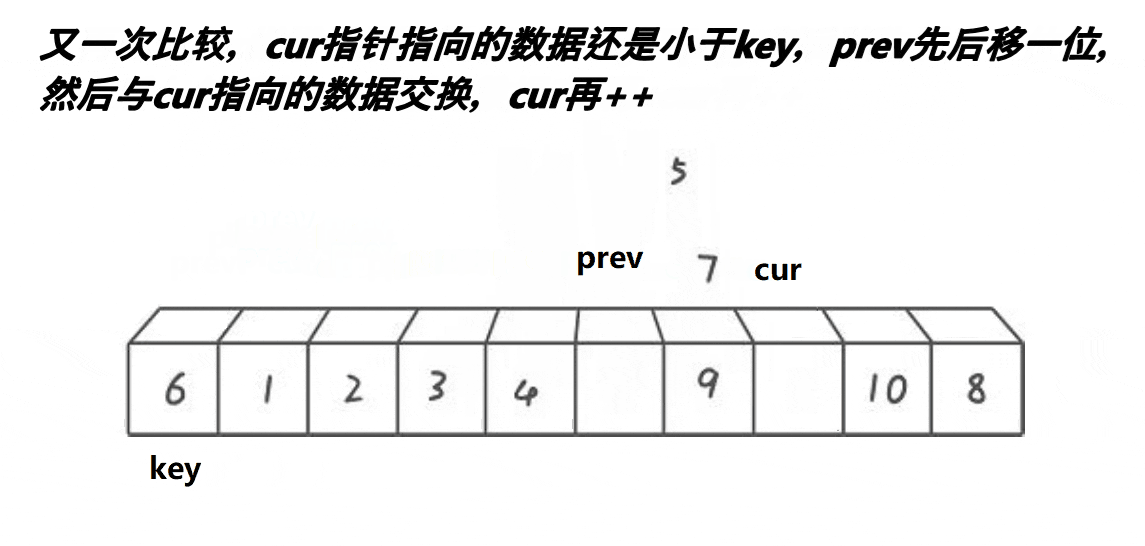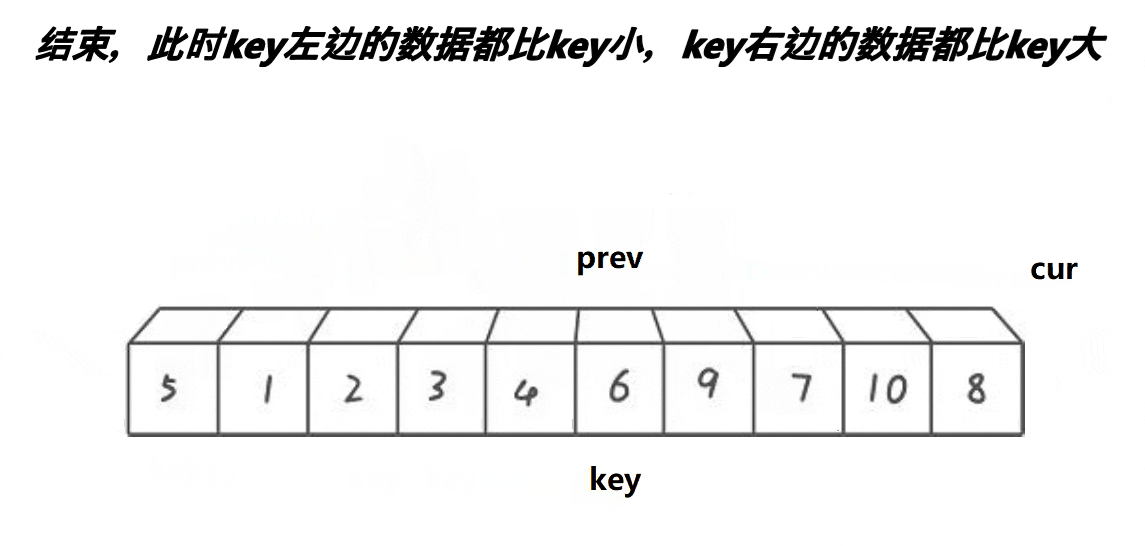
Basic idea:

1. Select an element key (usually the first), and then create two pointers prev and cur
2. At the beginning, the prev pointer points to the beginning of the sequence and the cur pointer points to prev+1
3. Cur starts moving until the element pointed to by cur is smaller than prev, and prev moves back one bit. If the position pointed to by prev is different from that pointed to by cur, exchange the elements at the two positions until cur reaches the end of the array, and finally exchange the data pointed to by key and prev
4. key, perform this operation on the left and right sides respectively, and recurse until there is only one data in the left and right sequences, or the left and right sequences do not exist to complete the sorting

Code implementation:

int PartSort(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = prev + 1;

	while (cur <= right)
	{
		// When cur points to data less than keyi points to data and prev
		// When different from cur, exchange the data pointed to by prev and cur
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[prev], &a[cur]);

		++cur;
	}
	Swap(&a[keyi], &a[prev]);

	return prev;
}
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = PartSort(a, left, right);
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

Non recursive version

Basic idea:

There are two methods to change recursion to non recursion: one is loop, and the other is to use data structure. Here, we use data structure stack

First put the left and right subscripts of the array into the stack, and then take the subscripts from the stack in each sorting. After sorting, put the left and right subscripts of the key into the stack, and repeat the above operations until there is only one data in the left and right sequences, or there is no data in the left and right sequences. Cancel the stacking. End sorting when stack is empty.

Code implementation:

void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	//Mark the left and right subscripts into the heap
	StackPush(&st, right);
	StackPush(&st, left);

	while (!StackEmpty(&st))
	{
		//Take the heap top data as the left and right subscripts
		int begin = StackTop(&st);
		StackPop(&st);

		int end = StackTop(&st);
		StackPop(&st);

		int keyi = PartSort3(a, begin, end);
		//Put the right half into the heap
		if (keyi + 1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, keyi + 1);
		}
		//Put the left half into the heap
		if (begin < keyi - 1)
		{
			StackPush(&st, keyi - 1);
			StackPush(&st, begin);
		}
	}

	StackDestroy(&st);
}

Fast scheduling optimization

When the value of the key is the maximum or minimum value, only the maximum or minimum value can be determined after one sorting, and the advantage of fast sorting cannot be reflected. Therefore, the key we determine is the middle value of the sequence. Here, the three number centring method is introduced.

The method of taking the middle of three numbers is to compare the leftmost, middle and rightmost numbers, take out the middle of three numbers and exchange them with the leftmost number

The code is as follows:

int GetMidIndex(int* a,int left,int right)
{
	//Take the middle number
	int mid = left + (right - left) / 2;
	//Compare left, center, right, and return the middle value
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] < a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[right] < a[left])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
}

Summary of quick sort features:

1. The overall comprehensive performance and usage scenarios of quick sort are relatively good, so we dare to call it quick sort
2. Time complexity: O(N*logN)
3. Space complexity: O(logN)
4. Stability: unstable

Merge sort

Recursive version

Dynamic diagram demonstration:

Merge sort is an effective sort algorithm based on merge operation. This algorithm is a very typical application of divide and conquer method. The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered.

Code implementation:

The idea of merging and sorting is not difficult. Open up a space of the same size as the original array, copy the data in the original array to the open space in order, and then copy the data back

void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
		return;

	int mid = (right + left) / 2;
	_MergeSort(a, left, mid, tmp);
	_MergeSort(a, mid + 1, right, tmp);
	// Merge
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int index = left;
	// Copy the data in the a array to the tmp array in order
	while (begin1 <= end1&&begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[index++] = a[begin1++];
		}
		else
		{
			tmp[index++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[index++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[index++] = a[begin2++];
	}

	// Copy the merged data back to the original array
	for (int i = left; i <= right; ++i)
	{
		a[i] = tmp[i];
	}
}

Non recursive version

The non recursive version of merge sort does not need to be completed with the help of stack. The purpose of sorting can be achieved through its own loop, but pay attention to the special situation of boundary

Special case I:

When the second interval element of the last group is less than gap, it is necessary to control the boundary of the interval so that its right boundary is n-1

Special case 2:

When the second interval of the last group does not exist, it is not necessary to merge the interval

Special case 3:

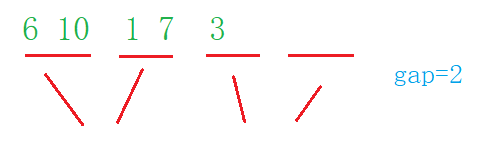
When the first interval element of the last group is less than gap, it is necessary to control the boundary of the interval so that its right boundary is n-1, which is similar to special case 1

Code implementation:

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	int grounpNum = 1;
	while (grounpNum < n)
	{
		for (int i = 0; i < n; i += 2 * grounpNum)
		{
			//Merge
			int begin1 = i, end1 = i + grounpNum - 1;
			int begin2 = i + grounpNum, end2 = i + grounpNum * 2 - 1;
			int index = begin1;

			//[begin2,end2] nonexistence is corrected to a nonexistent interval
			if (begin2 >= n)
			{
				begin2 = n + 1;
				end2 = n;
			}

			//end1 is out of bounds. Fix it
			if (end1 >= n)
			{
				end1 = n - 1;
			}

			//end2 is out of bounds. Fix it
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			// Copy the data in the a array to the tmp array in order
			while (begin1 <= end1&&begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];
			}
		}

		// Copy the merged data back to the original array
		for (int i = 0; i < n; ++i)
		{
			a[i] = tmp[i];
		}
		grounpNum *= 2;
	}
	free(tmp);
}

Summary of characteristics of merge sort:

1. The disadvantage of merging is the spatial complexity of O(N)
2. Time complexity: O(N*logN)
3. Space complexity: O(N)
4. Stability: stable