Classification: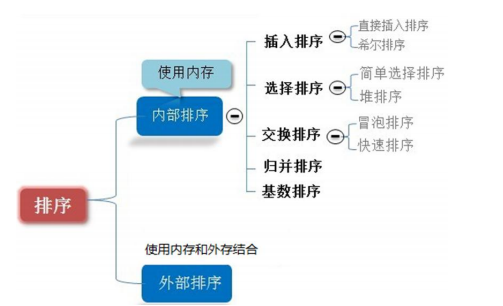
1. Bubble sorting: (Average time complexity: O(n^2))
1. Basic idea: By comparing the values of adjacent elements from front to back in the column to be sorted, and then exchanging them in reverse order, the larger elements move forward and backward gradually, rising up like bubbles under water. Each round of sorting will result in the maximum number of last elements in the sorting sequence.
2. Algorithmic optimization: In the sorting process, if there is no over-exchange during a comparison, the current sequence has been ordered, and the next sorting is no longer needed. Therefore, setting a flag to determine whether elements have been exchanged during the sorting process can be optimized appropriately.
3. Examples of demonstrating the bubble sorting process:
Summarize the above examples:
(1) Length of a row of arrays together - a sort cycle
(2) The number of sorting trips is continuously decreasing
(3) If no exchange is found in a lie, it may end early
4. The code is as follows:
public static void bubbleSort(int[] arr){
int temp = 0;
boolean flag = false;//Optimize
for(int i = 0; i < arr.length - 1; i++){
for(int j = 0; j < arr.length - 1 - i; j++){
if(arr[j] > arr[j + 1]){
flag = true;
temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
}
}
if(!flag){
break;
}else{
flag = false;
}
}
}
Interpretation: (1) The outer loop controls the number of cycles (the length of the sequence to be sorted - 1), and the inner loop controls the exchange of adjacent elements, paying attention to the exchange conditions (j < arr.length - 1 -i).
(2) At the end of a cycle, if flag is set to true, then it is an ordered sequence, not another cycle.
2. Quick sorting: (an improvement on bubble sorting) (Average time complexity: O(nlogn))
1. Basic idea: Select a baseline element in the sequence to be sorted, divide the sequence into two separate parts after a single sorting, the left part is smaller than the baseline, the right part is larger than the baseline, and then process the two parts recursively, to achieve the goal again.
2. Quick Sort Diagram:
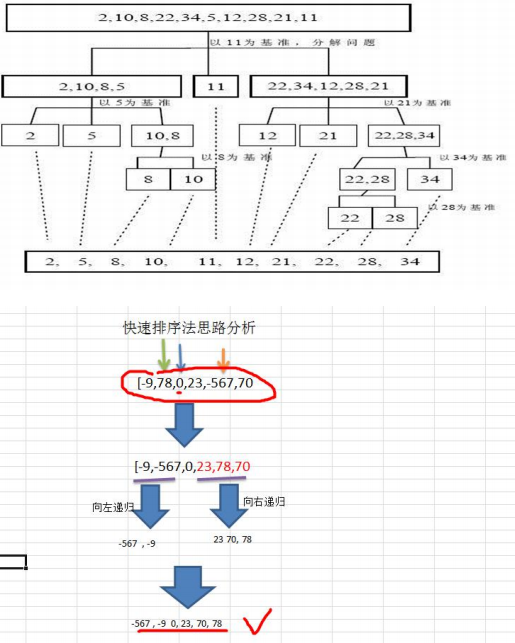
3. The code is as follows:
public static void quickSort(int[] arr,int start,int end){
if(start >= end){//Recursive End Flag
return;
}
//Use the number 0 in the array as the standard number
int stard = arr[start];
int low = start;
int high = end;
while (low < high) {
while (low < high && stard <= arr[high]){
high --;
}//Find a number smaller than stard on the right
arr[low] = arr[high];//Number marked low for override after finding
while (low < high && stard >= arr[low]){
low ++;
}//Find a number larger than stard on the left
arr[high] = arr[low];//Number marked high for overwriting after finding
}
//Assign a standard number to a number marked low or high (low=high in this case)
arr[low] = stard;
//Recursively process numbers on both sides
quickSort(arr,start,low);
quickSort(arr,low+1,end);
}Note: (1) Any recursion must be aware of the end flag and will inevitably end up in an infinite loop.
(2) In this algorithm, the number 0 is selected as the standard number, so when a number is found on the right, which is smaller than the base, it can be directly assigned to the number labeled low on the left(No, of course.) It may not be the same in detail as the algorithm, but the general idea remains the same.
3. Merge Sort: (Average Time Complexity: O(nlogn))
1. Basic idea: is a sorting algorithm implemented by the idea of merging, which uses a classical partition strategy (divide: divide the problem into smaller problems and solve them recursively, cure: patch up the answers obtained in stages. divide and conquer).
2. Merge Sort illustration:
Divide and conquer overall illustration:
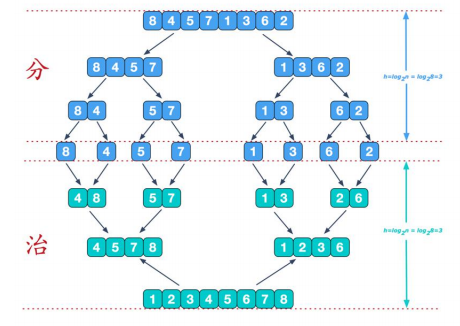
Illustration of merger during the governance phase:
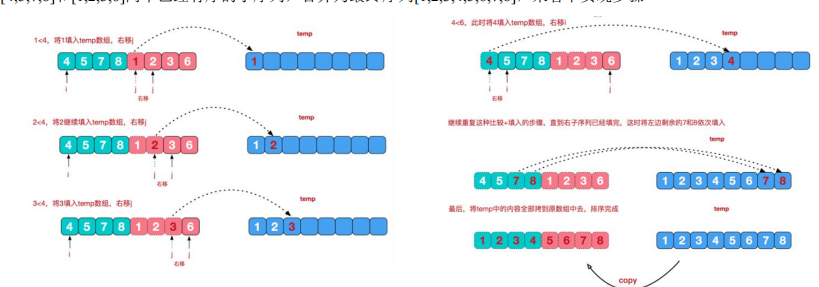
3. The code is as follows:
//Division+Combination Method
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if(left < right){
int mid = (left + right) / 2;
//Decomposition recursively to the left
mergeSort(arr,left,mid,temp);
//Decomposition Recursively Right
mergeSort(arr,mid + 1,right,temp);
//To merge
merge(arr,left,mid,right,temp);
}
}
//Method of merging
/**
*
* @param arr Sorted original array
* @param left Initial index of left ordered sequence
* @param mid Intermediate Index
* @param right Right Index
* @param temp Array to be transferred
*/
public static void merge(int[] arr,int left,int mid,int right,int[] temp) {
int i = left;//Initial index of left ordered sequence
int j =mid + 1;//Initial index of right ordered sequence
int t = 0;//Current index to temp array
//1. Fill the temp array with two ordered sequences according to the rules until one party has finished processing
while (i <= mid && j <= right) {
if(arr[i] <= arr[j]){
temp[t] = arr[i];
t++;
i++;
}else{
temp[t] = arr[j];
t++;
j++;
}
}
//2. Fill the temp array directly with an ordered sequence of remaining data
while (i <= mid){
temp[t] = arr[i];
t++;
i++;
}
while (j <= right){
temp[t] = arr[j];
t++;
j++;
}
//3. Copy elements of temp array to arr (not all)
t = 0;
int tempLeft = left;
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t++;
tempLeft++;
}
}Interpretation: In the margeSort() method, the order to be sorted at this time is listed as shown in the figure after the right recursion has been decomposed:
You can see that there are eight small ordered sequences, and then from this point on the small ordered sequences are merged, until the backtracking is complete, the order is already sorted.
4. Sorting cardinality: (Average time complexity: O(n^k))
1. Introduction: Cardinality sorting is an extension of bucket sorting. It cuts integers into bits and assigns corresponding elements to some buckets according to the number of bits they get. Cardinality sorting is an efficient and stable sorting method (for the same elements, the relative order before and after sorting is unchanged).
2. The main idea is to unify all the values to be compared into the same number of digits, with the shorter digits preceded by 0. Then, start with the lowest digit and sort them one by one. Then, the columns are sorted from the lowest to the highest digit.
3. Graphic description of cardinality sorting: (The highest number of digits in the sequence is 100, so sort three times)
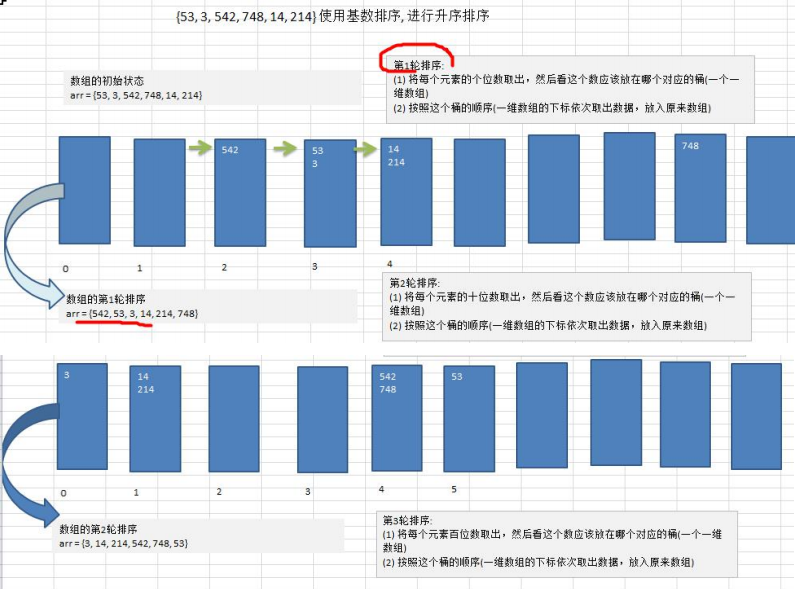
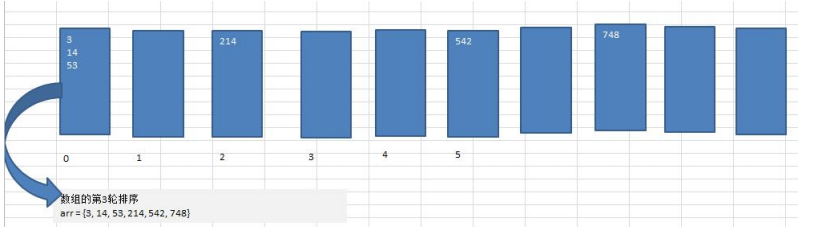
4. The code is as follows:
public static void radixSort(int[] arr){
//Preparing to start the cycle
//1. Get the maximum number of digits in the array
int max = arr[0];
for(int i = 1; i < arr.length; i++){
if(arr[i] > max){
max = arr[i];
}
}
//2. How many digits is the maximum number obtained
int maxLength = (max + "").length();
//Defines a two-dimensional array of 10 buckets, each of which is a one-dimensional array
//1. A two-dimensional array contains 10 one-dimensional arrays
//2. To prevent data overflow when placing data, the length of one-dimensional array is arr.length
//3. It is obvious that cardinality ordering is a classical algorithm for space-time conversion.
int[][] bucket = new int[10][arr.length];
//To record how much data is actually stored in each bucket, we define a one-dimensional array to record the number of data each bucket puts in.
int[] bucketElementCounts = new int[10];
//bucketElementCounts[0], which records the number of buckets [0] buckets put in
for(int i = 0, n = 1; i < maxLength; i++,n *= 10){
//Sort the number of digits corresponding to each element for each round (first one, second ten.)
for(int j = 0; j < arr.length; j++){
//Remove the value of each element's corresponding position and place it in the corresponding bucket
int digtiofElement = arr[j] / n % 10;
bucket[digtiofElement][bucketElementCounts[digtiofElement]] = arr[j];
bucketElementCounts[digtiofElement]++;
//For example, 53 means that when placed in bucket[3][bucketElementCounts[3], bucketElementCounts[3] starts at 0 and goes on for every number +
}
//In the order of this bucket, (the subscript of a one-dimensional array takes out the data and puts it in the original array)
int index = 0;
//Traverse through each bucket, and if there is data in the bucket, place it in the original array
for(int k = 0; k < bucketElementCounts.length; k++){
if(bucketElementCounts[k] != 0){
//Loop the kth bucket (that is, the kth one-dimensional array) into the
for(int l = 0; l<bucketElementCounts[k] ; l++){
arr[index] = bucket[k][l];
index++;
}
}
//For each round of processing, you need to set the array for each bucket count to 0
bucketElementCounts[k] = 0;
}
}
}