Title Description:

Given a source string and a target string, the following operations can be performed on the source string:
Insert a character at any position;
Replace any character;
Delete any character.
Write a program to return the minimum number of operations, so that the source string is equal to the target string after the above operations (the length of the source string and the target string is less than 2000).

Resolution:

To get the editing distance problem, the simplest idea is to traverse all solutions violently, that is, use DFS or BFS + priority queue to store the results of each traverse, and finally find the optimal solution. Obviously, this idea has low feasibility and high time and space complexity. After thinking, I found that the optimal solution of the editing distance problem includes the optimal solution of the subproblem, and the solution of its independent subproblem has been repeatedly calculated many times. Therefore, the editing distance problem can be divided into several smaller subproblems, which is in line with the characteristics and basic idea of dynamic programming.
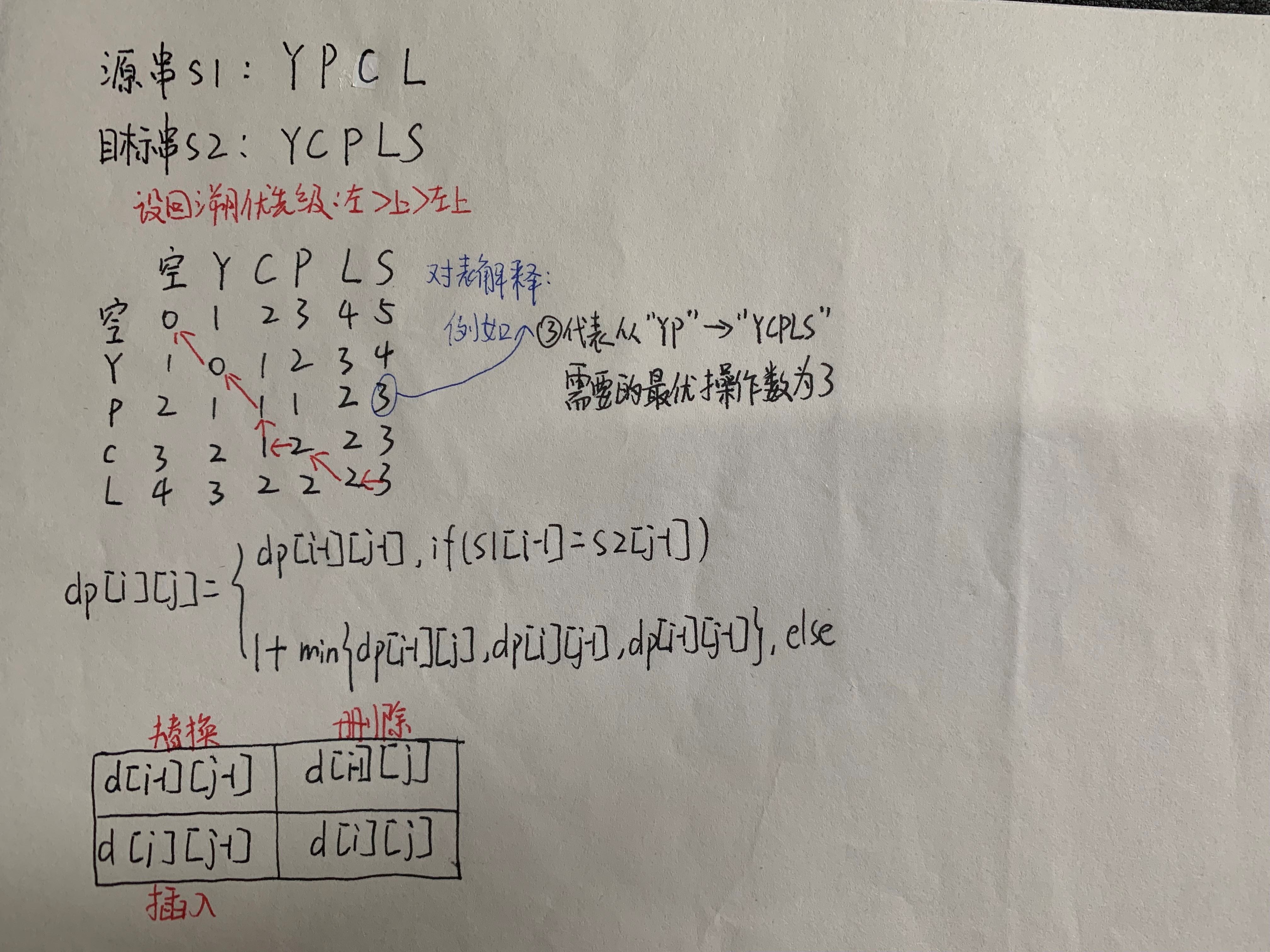
First, define such an array - dp[len1+1][len2+1], where len1 and len2 represent the length of the input source string and target string respectively. dp[i][j] represents the minimum number of operation steps required to convert the first I characters of the source string to the first j characters of the target string.

After induction and derivation, the state transition equation of dynamic programming is obtained:

Design:

1. Dynamic programming to find the minimum operand (find the optimal solution):
   The core idea is to initialize dp Table + apply state transition equation;
   

2. Backtracking output conversion process:
   Starting from the result dp[len1][len2] and backtracking from bottom to top, there are four branches. Compare the values of dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+1, dp[i-1][j-1] and dp[i][j].
   Because the backtracking results are inverted, a text stream is used in the actual code to store the backtracking results in reverse order, and the output is in positive order.
   

analysis:

Let m=len(source_str); n=len(target_str);

1. Time complexity analysis:
   When the dp table is established by dynamic programming, there are two-layer for loops, and the time complexity is O(mn);
   During backtracking, a layer of while loop with time complexity of O(max{m,n});
   Therefore, the total time complexity of this program is O(mn);
2. Spatial complexity analysis:
   A two-dimensional array dp[m][n] is developed, and the space complexity is O(mn);

Solution:

#include <bits/stdc++.h>
using namespace std;
int main(){
	string source_str, target_str;
	stringstream line;	// Remember the contents of the first line of output to avoid one more cycle 
	cout<<"Source string: "; cin>>source_str;
	cout<<"Target string: "; cin>>target_str;
	int len1 = source_str.length(), len2 = target_str.length();
	int dp[len1+1][len2+1];	// dp[i][j] stands for source_str first I characters → target_ The minimum number of steps required for the first j characters of str 
	cout<<"--------------------------------------------"<<endl<<" ";
	for(int j = 0; j <= len2; ++j) {	// Initialize dp array and output header 
		dp[0][j] = j;
		if(j == 0) cout<<" empty ";
		else cout<<target_str[j-1]<<" ";
		line<<j<<" ";
	} 
	cout<<endl<<"empty "<<line.str();
	for(int i = 0; i <= len1; ++i) {	// Initialize dp array and output header
		dp[i][0] = i;
	} 
	cout<<endl;
	// Core code
	for(int i = 1; i <= len1; ++i) {
		cout<<" "<<source_str[i-1]<<" "<<i<<" ";
		for(int j = 1; j <= len2; ++j) {
			if(source_str[i-1] == target_str[j-1]){		// If the current characters are equal, dp[i][j]=dp[i-1][j-1] 
				dp[i][j] = dp[i-1][j-1];
			}
			else{	// 1. Replacement: D [i] [J] = D [I-1] [J-1] + 1; 2.target_ The letter STR is inserted into source_str:d[i][j] = d[i][j-1] + 1; 3. Delete source_ Letters of STR: d[i][j] = d[i-1][j] + 1;
				dp[i][j] = 1 + min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]));
			}
			cout<<dp[i][j]<<" ";
		}
		cout<<endl;
	}
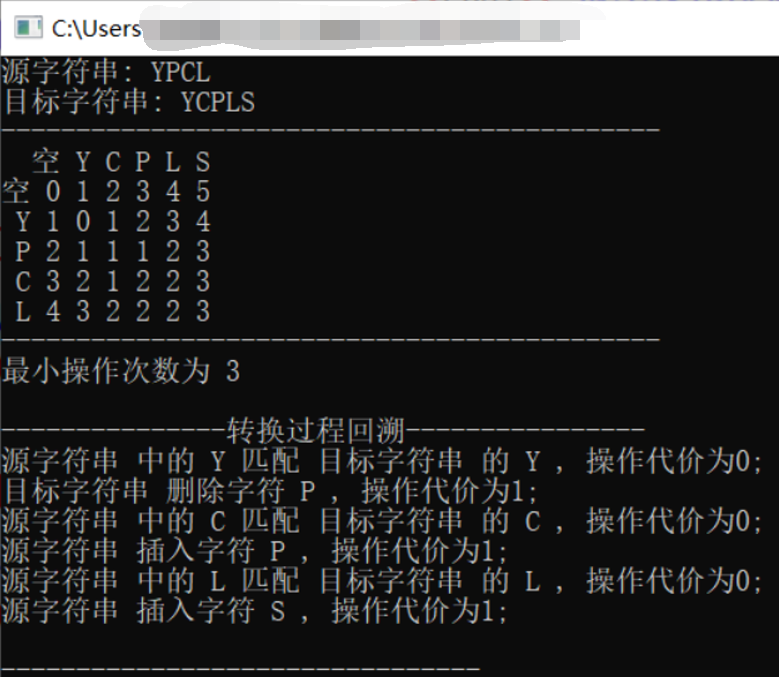
	cout<<"--------------------------------------------"<<endl<<"The minimum number of operations is "<<dp[len1][len2]<<endl<<endl;
	cout<<"---------------Conversion process backtracking----------------"<<endl;
	int i = len1, j = len2 ;
	int mindis = dp[i][j];
	string performs = "";
	while(i > 0 && j > 0) {
		if(dp[i][j-1]+1 == dp[i][j]) {			// mindis = d[i][j-1];
			stringstream perform;
			perform<<"Insert character from source string "<<target_str[j-1]<<" , The operation cost is 1;"<<endl;
			performs = perform.str() + performs;
			j--;
		} 
		else if(dp[i-1][j]+1 == dp[i][j]) {		// mindis = d[i-1][j];
			stringstream perform;
			perform<<"Target string delete character "<<source_str[i-1]<<" , The operation cost is 1;"<<endl;
			performs = perform.str() + performs;
			i--;
		} 
		else if(dp[i-1][j-1]+1 == dp[i][j]) {	// mindis = d[i-1][j-1];
			stringstream perform;
			perform<<"In source string "<<source_str[i-1]<<" Replace with the of the target string "<<target_str[j-1]<<" , The operation cost is 1;"<<endl;
			performs = perform.str() + performs;
			i--; j--;
		} 
		else if(dp[i-1][j-1] == dp[i][j]) {		// d[i][j] = d[i-1][j-1];
			stringstream perform;
			perform<<"In source string "<<source_str[i-1]<<" Matching target string "<<target_str[j-1]<<" , The operation cost is 0;"<<endl;
			performs = perform.str() + performs;
			i--; j--;
		} 
		else {
			i--; j--;
		}
	}
	cout<<performs;
	return 0;
}