1. Introduction
1.1 what is dynamic programming?
Dynamic Programming is a mathematical method of optimization in the solution process (also known as global optimization). The multi-step process is transformed into a series of single-step problems, which are solved one by one by using the relationship between each step.
(dynamic programming is a widely used problem solving method, not a specific algorithm, but an idea and a means)
1.2 when to use dynamic programming
In a word, if the global optimal solution of a problem (usually the maximum value or the shortest length, etc.) is required, and the problem can be decomposed into several subproblems, and there are overlapping subproblems between small problems, dynamic programming is considered. (similar to the recursive idea, the idea of making big things small and making small things small)
Problems that can be solved by dynamic programming generally have three properties:
- Optimization principle
If the solution of the subproblem contained in the optimal solution of the problem is also optimal, it is said that the problem has an optimal substructure, that is, it satisfies the optimization principle. (that is, big problems are decomposed into small problems) - No aftereffect
That is, after a certain status or step, the status that is not updated in the future will not be affected by future decisions (i.e. inheritance relationship) - Overlapping subproblem
That is, subproblems are not independent, and a subproblem may be used many times in the next stage of decision-making. (this property is not a necessary condition for the application of dynamic programming, but without this property, the dynamic programming algorithm has no advantages over other algorithms) (for example, the local optimal problem is independent between subproblems, so it is better to use greedy thought) (that is, the current state is related to the previous state when it is updated)
2. Fibonacci sequence and extension problem (dp introduction)
2.1 Fibonacci series
f(n) = f(n-1) + f(n-2) (n >= 2)
2.2 problem introduction
Cow Reproduction : a cow. It gives birth to a heifer every year. Each heifer starts from the fourth year and gives birth to a heifer at the beginning of each year. Please program how many cows are there in the nth year?
2.21 recursive divide and conquer solution
int fib(n){
if(n < 2) return n;
return f(n-1) + f(n-4);
}
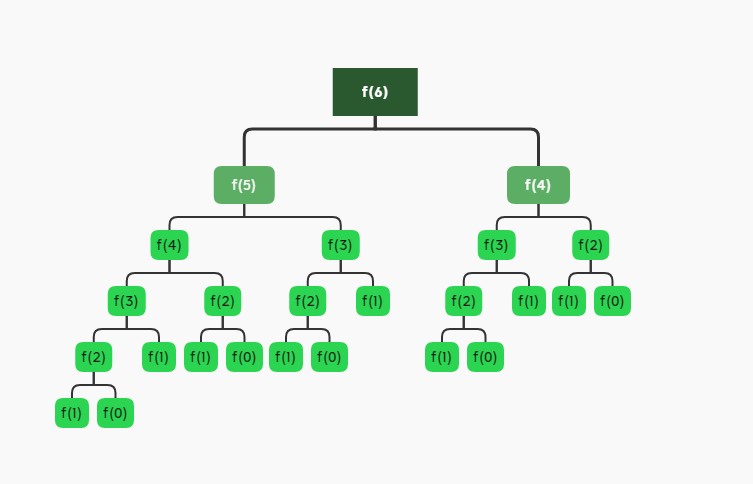
However, the time complexity after rough calculation is a little large (O(sqrt(2)n). When the value of n is 60, it takes a lot of time to calculate, so it is necessary to introduce a new method
2.22 using memory search to reduce time complexity
Therefore, memory search is introduced to save the calculated part in the array
f[1] = 1;
f[0] = 0;
int fib(n){
if(f[n] != 0) return f[n];
return f[n] = f(n-1) + f(n-2);
}
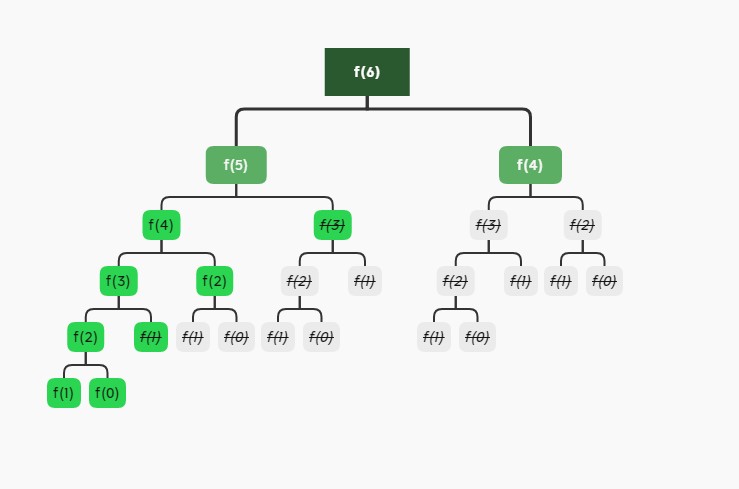
In this way, the time complexity will be reduced to O(n)
3. Shortest down / up path problem
3.1 digital triangle problem
Digital triangle [Luogu P1216]
Write a program to find the path ending anywhere from the highest point to the bottom, so that the path passes through the sum of numbers. Each step can go to the lower left point or the lower right point.
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
In the above example, the path from 7 → 3 → 8 → 7 → 5 produces the maximum
It is necessary to consider the problem of global optimization, rather than just considering the way ahead
The key to dp is to list the dynamic equations
dp[i][j] = max(dp[i-1][j],dp[i-1][j+1]); //i represents the number of rows, from bottom to top; j represents the number of columns, from left to right
Indicates that the longest path value of the current step is related to the point of the previous step and the point on the right of the previous step. The maximum value of each layer from bottom to top is related to the value of the corresponding next layer. By forming this relationship, each layer stores the maximum value extending from bottom to top, and the maximum sequence sum will be generated at the first layer
Here, let's briefly say that this dynamic equation satisfies dp three properties. The following problems need to be considered by yourself:
1. Optimization principle: to find the maximum path, I decompose it into the maximum path to a certain point, and then through layer by layer summary traversal, I can find the maximum value of all paths in each layer to the top point of the triangle.
2. No aftereffect: for example, the longest length value of the first layer has nothing to do with that of the third layer, that is, judging the longest length of the first layer will not affect the longest length of the third layer, because the longest value has been saved and will not be changed
3. There are overlapping subproblems: for example, when reaching the maximum value of a certain path at the third point of the third layer, either the third value of the fourth layer or the fourth value may be used. It is necessary to determine which path to take to make its value greater. The two paths may be the same, so there will be overlapping subproblems
If you don't understand the three properties of dp, you can read it again, because if you understand these three properties, you will better understand other dp problems that are difficult to understand in the future
4. Longest Manhattan path problem
4.1 problem description LMP(Longest Manhattan Path)
n formed by a nonnegative integer × m matrix, find a path from the upper left corner to the lower right corner to maximize the total length of the path (the sum of integers along the way) (you can only go right or down inside the matrix)
4.2 using dynamic programming to solve
Here, similar to the previous problem, the dynamic equation can be listed by considering the relationship between each two inclined layers:
dp[i][j] = max(dp[i][j+1],dp[i+1][j]) + w[i][j];
From top left to bottom right, consider the problem step by step, and finally put the whole sheet n × m maps are assigned once. The dynamic array dp represents the maximum distance of the upper left point, and the point at the lower right is the collection of the maximum points. In this way, the dynamic equation can be used to solve the optimal problem
4.3 memory search
Of course, this problem can also be solved by memory search. Considering the state at the bottom right, dfs is used to record and run upward at one time.
return dp[i][j] = max{d(i-1,j),d(i,j-1)} + w[i][j];
The details will not be expanded. Interested students can find template questions to try. If you still want to learn, you can come to me directly
4.4 development issues
Hamanton distance (template topic, which has nothing to do with dp, you can let go and learn)
Title Link
describe
There are many residents in a block. The streets of the block can only be east-west and North-South directions.
Residents can only walk along the street.
The streets are equally spaced.
Use (x,y) to represent the block where the resident is sitting.
For example (4,20), it means that the user has the 4th Street in the east-west direction and the 20th Street in the north-south direction.
Now we need to build a post office to minimize the sum of the distances from each household to the post office.
Now the post office should be built in that place to minimize the sum of all residents;
input
The first line is an integer n<20,Indicates yes n Group test data, here is n Group data; The first line of each group is an integer m<20,Indicates that this group has m Residents, below m that 's ok Each line has two integers 0<x,y<100,Represents the coordinates of a user's block. m After the row is a new set of data;
output
The minimum distance and of each group of data output to the post office, and the carriage return ends;
First, consider the distance between two points (that is, Manhattan distance), because we can only walk blocks
So the distance from (xi,yi) to (xj,yj) must be | xi - xj| + |yi - yj|
Because there is no straight line between two points, it must go from the horizontal and vertical directions of the block, so the distance is the sum of the absolute values of x and y
To find the minimum value from multiple points to a certain point, let's consider that two points arrive
The method of the minimum distance of the end point is to focus on the distance between these two points, otherwise it will be too long
The path is included. For the three points, shall we put the end point in the middle
It can make the path shortest, because the end point is always an extra section in other positions (you can draw your own picture and consider it)
For 4 points and above, we still put them in the middle to minimize the path (i won't say it here. This is a type question. If you want to prove it, please refer to i other people's blogs)
In order to solve the problem, we consider that the method is to sort the values of X and y axes, and then turn the end point into the middle point of these x and y points. The absolute values of the maximum and minimum values are the distance from two points to the end point
Then consider all the cases, and find the minimum length
After ordering arrays a and b, the dynamic equation is
for(int i = 1;i < m/2;i++) sum += a[m-i-1] - a[i] + b[m-i-1] - b[i];
5. LIS Longest Increasing Subsequence
5.1 problem description
Give you a number, such as 4 1 3 5 2, so that you can find the longest ascending subsequence in this number? (sometimes the longest non decreasing subsequence is asked. Pay attention to judge whether the same situation needs to be considered)
5.2 normal thinking
definition:
a[i] Store all digital sequences dp[i][j] Indicates on page i Judge from 1 point - i One of j Is the of the point less than i The value of the point and stores the maximum length
Starting from a point (also called analyzing a number), judge whether the previous number is greater than it. If so, keep the length of this number plus one in the dp state greater than its number. If not, keep the current length as 1 (starting from the first one, find the ascending sequence again). for loop traversal considers all points. When considering the point whose length has just been increased by one, it is judged that there is also a point greater than it after it, and then the operation is the same as above. According to this, at the last point, it indicates the length of all paths from several points to the last, and then output dp[n][n]
for(int i = 1;i <= n;i++) dp[i][1] = 1; for(int j = 1;j <= i;j++) if(a[i] > a[j]) dp[i][j] = max(dp[i][j]+1,dp[i][i]);
This is a better two-dimensional dynamic method, but the time complexity is too high, and 104 ~ 105 data will be stuck, so there is another way to optimize the time complexity
5.3 using dichotomy to optimize time
In fact, it is not difficult to see that for n2, it is actually violent enumeration: compare each state separately. But in fact, some unnecessary state enumeration results in a waste of time. When the number of elements reaches more than 104 ~ 105, it has timed out. At this time, we can reduce the time complexity through another dynamic programming method:
definition:
f[num] Indicates the current maximum length num Minimum tail element value of, last num Is the longest sequence
Then, if the end element of the subsequence of this length is smaller, the subsequent elements can be more easily added to the ascending subsequence that we speculate can be used as a result.
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
f[i]=0x7fffffff;
//The initial value should be set to INF
/*The reason is very simple. Every time a new element is encountered, it will be the longest recorded by the recorded f array
Compare the end element of the ascending subsequence: if it is less than this element, keep looking forward until it is found
An element just larger than it, replace; On the contrary, if it is greater than, fill in the next q, INF of the end element
Just to facilitate backward replacement!*/
}
f[1]=a[1];
int len=1;//The number is obtained by recording the effective digits of the f array
/*Because as mentioned above, we may have to keep looking forward,
Therefore, the strategy of binary search can be adopted, which is to make the time complex
The key factor to reduce the degree to nlogn level.*/
for(int i=2;i<=n;i++)
{
int l=0,r=len,mid;
if(a[i]>f[len])f[++len]=a[i];
//If it is just greater than the end, fill it back in sequence temporarily
else
{
while(l<r)
{
mid=(l+r)/2;
if(f[mid]>a[i])r=mid;
//If it is still less than the minimum end of the previous record, continue
//Look forward (because it is the longest ascending subsequence, the f array must be
//(monotonous)
else l=mid+1;
}
f[l]=min(a[i],f[l]);//Update minimum end
}
}
cout<<len;
That is: use array f to record the end value of the maximum rising sequence. Once it is greater than the end value, it will be added directly. Otherwise, replace a number greater than the previous one by binary search
5.4 similar examples
Luogu [P1020]
The first problem is to consider the longest non increasing sequence, and the second problem is to find the maximum increasing sequence again, which is the minimum number of times. Specific analysis can also be learned with reference to problem solving
6. Longest common subsequence (LCS)
6.1 problem description
Given two strings, what is the longest length in the common subsequence of two strings? Which is it?
6.2 substring and subsequence
Substring
A continuous part of the original string
Subsequnce
A string composed of any number of characters extracted from the original string (it can be discontinuous, but the order cannot be changed)
6.3 normal method considerations
For example, given sequence:
3 2 1 5 4 1 5 2 4 3
After judging that each character is the same, the dynamic equation must be compared with the previous situation, whether the size can meet the update (meet the longest sequence), how to assign the value, and how to transfer the state if not
We use the array dp[i][j] to represent the LCS length of the first I of the first row and the first j of the second row, and then consider the progress of each step.
When the two line sequences A,B and the current two elements (A[i], B[i]) are different, consider inheritance:
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
When the two line sequences A,B and the current two elements (A[i], B[i]) are the same, consider updating:
dp[i][j] = max(dp[i][j],dp[i-1[j-1]+1]);
The specific codes are as follows
#include<stdio.h>
int max(int a,int b){
return a>=b?a:b;
}
int a[1010];
int b[1010];
int dp[1010][1010] = {0};
int main()
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
for(int i = 1;i <= n;i++) scanf("%d",&b[i]);
int s = 0;
for(int i = 1;i <= 1000;i++){
for(int j = 1;j <= 1000;j++){
dp[i][j] = max(dp[i-1][j],dp[i][j-1]); //Do not consider inheritance for updates
if(a[i] == b[j]) dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1); //If the same, consider updating
}
}
printf("%d",dp[n][n]); //Finally, the first n numbers of the first line and the first n numbers of the second line can be output with the longest LCS
return 0;
}
6.3 dichotomy optimization
The above algorithm requires n2 time complexity, and the array cannot be opened too large, so we consider a method to transform the LCS problem into LIS problem, and use the dichotomy to optimize it.
No. 1 2 3 4 5 A[] = 3 2 1 5 4 B[] = 1 5 2 4 3
Now we introduce A new array t [] to realize the number mapping of the array. Because the elements of A and B are the same and are A permutation and combination of 1-n numbers, we consider this
Serial number i 1 2 3 4 5 A[] = 3 2 1 5 4 t[A[i]]=i 3 2 1 5 4 B[i]=t[A[i]] 3 4 2 5 1
So obviously, if the number in t increases
Then, indicating that the sequence number in A is increasing means that the increasing sequence is A subsequence of A, and we always traverse the sequence in B (from front to back). Obviously, this sequence is also A subsequence of B, so this sequence is the common subsequence of A and B
For understanding, you can find the subscript of array t through the element value in B, which corresponds to the value of the element in A. in this way, you can bring it in twice for understanding
Then maximizing this subsequence is the LIS algorithm that maximizes the longest ascending subsequence in the t array
In this way, we turn the LCS problem into a LIS problem and solve it with n log n.
The code is as follows
#include<stdio.h>
int a[100001];
int t[100010];
int b[100010];
int min(int a,int b){
return a>=b?b:a;
}
int main()
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;i++){
scanf("%d",&a[i]);
t[a[i]] = i; //a array exists in t array
}
int f[100010] = {0};
for(int i = 1;i <= n;i++){
int k;
scanf("%d",&k);
b[i] = t[k]; //Store the element in the B array according to the subscript of the value of the element in the second row in the array t
f[i] = 0x7fffffff;
}
int num = 0;
for(int i = 1;i <= n;i++){ //Find the longest increasing sequence by bisection with LIS
if(b[i] >= f[num]) f[++num] = b[i];
else{
int l = 0,r = num,mid;
while(l < r){ //Generally, binary search is used to find a certain number (or surrounding numbers)
mid = (l+r)/2;
if(f[mid] > b[i]) r = mid; //This part of assignment is to find the largest value less than b[i] and the smallest value greater than b[i]
else l = mid+1;
}
f[l] = min(f[l],b[i]);
}
}
printf("%d",num); //The last output num is the same subsequence of 1
return 0;
}
6.4 other issues
There is also a dynamic programming problem about linear strings, which is a little similar to this topic. You can learn it when you have time. It is also a template problem
Matching subsequence of strings
7. Summary
Generally, the simple problems related to linear dynamic programming are just these models, which have not been developed in depth. When encountering specific problems, think again and learn again. Because there are many changes in dynamic programming, you need to master the basic types and expand others yourself.
The key to dynamic programming is application. If you finish learning, you can do more topics to consolidate + more understanding of dynamic programming
The next problem to be solved is the knapsack problem. Only five kinds of knapsack deformation problems are written. In this way, the most basic dynamic programming problems are ok. You can take time to learn.