1, Foreword
AcWing algorithm improves the content of the course. This paper explains dynamic programming lesson 1: mathematical triangle model
This article includes the following topics:
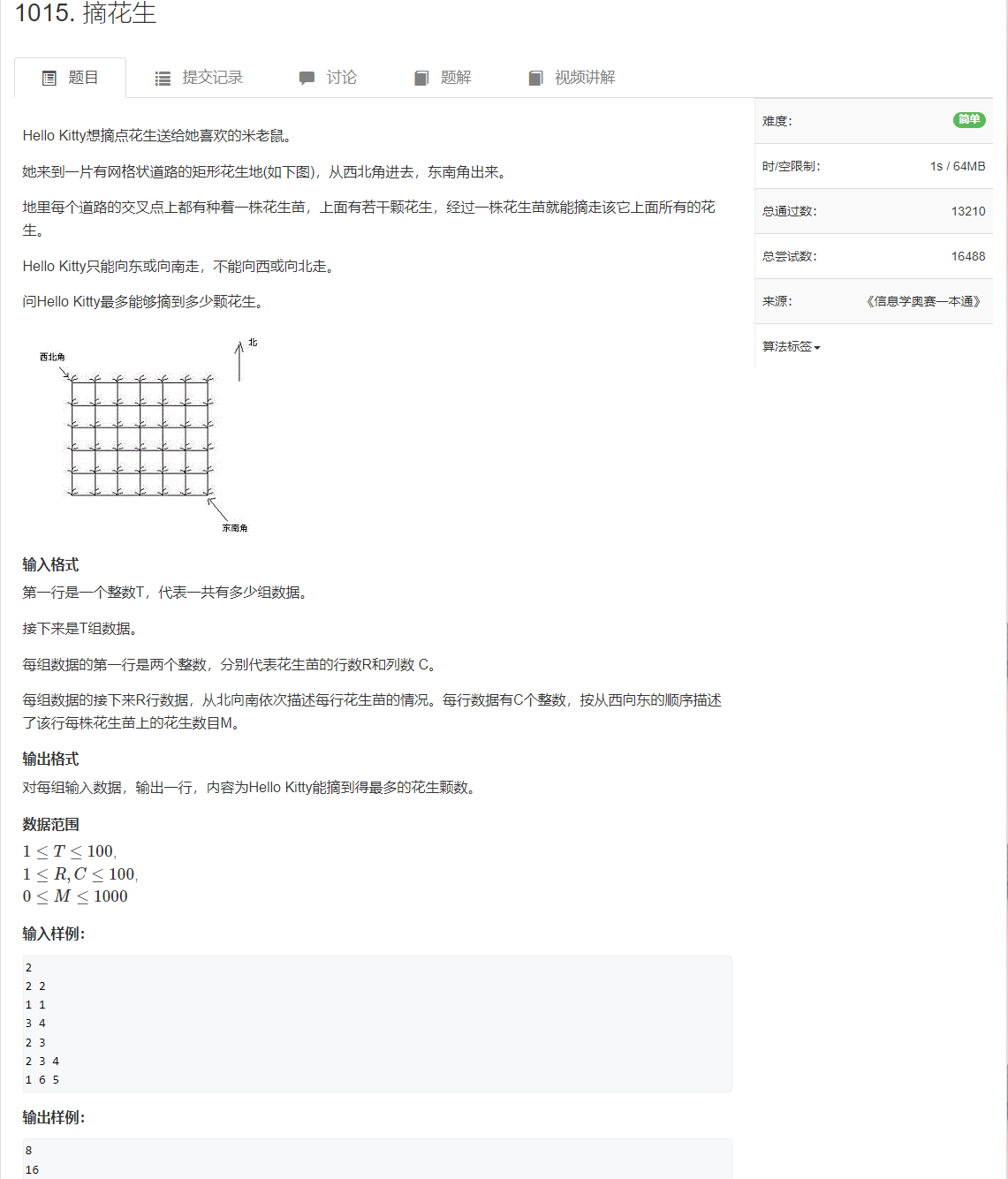
AcWing 1015. Picking flowers
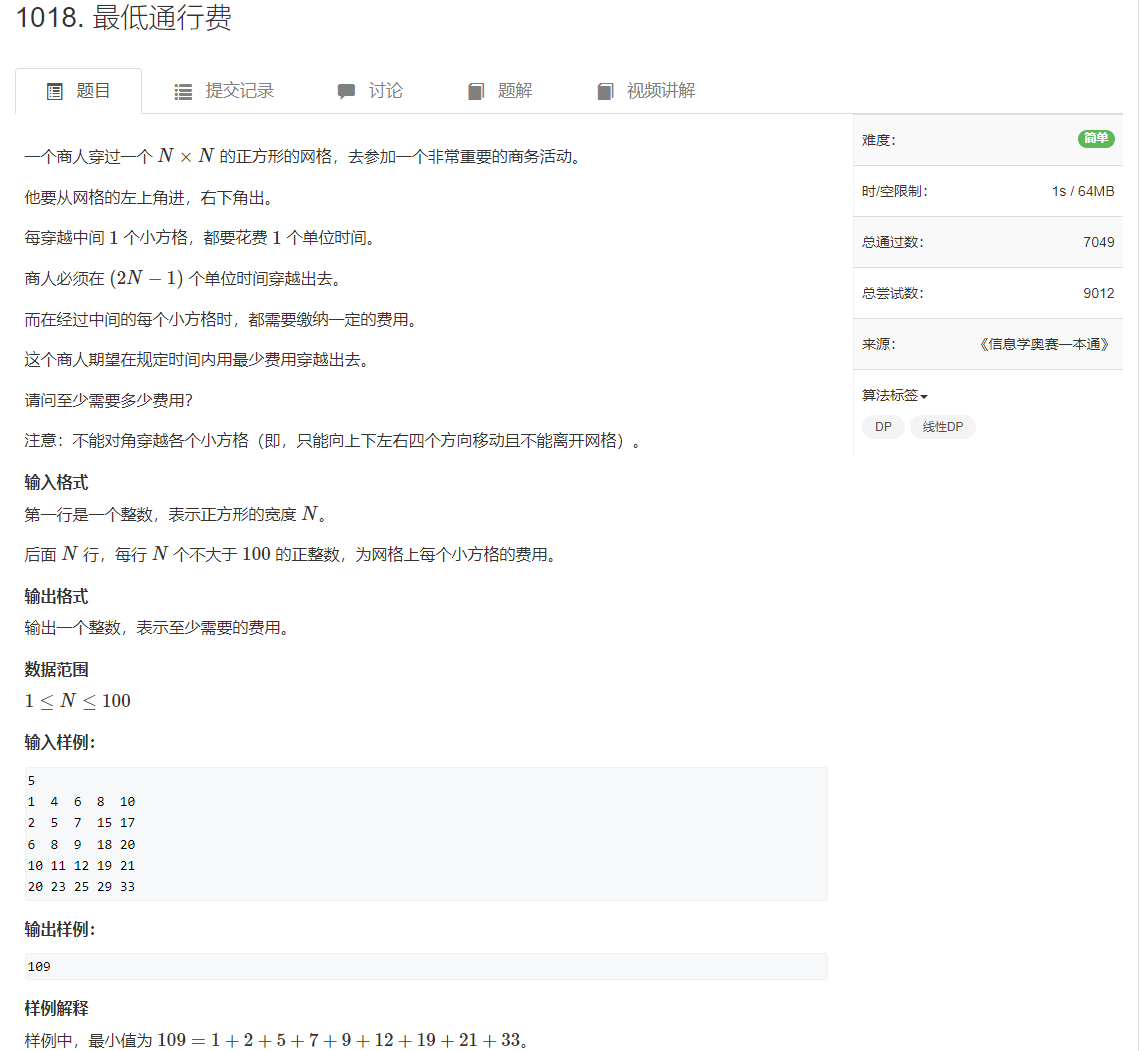
AcWing 1018. Minimum toll
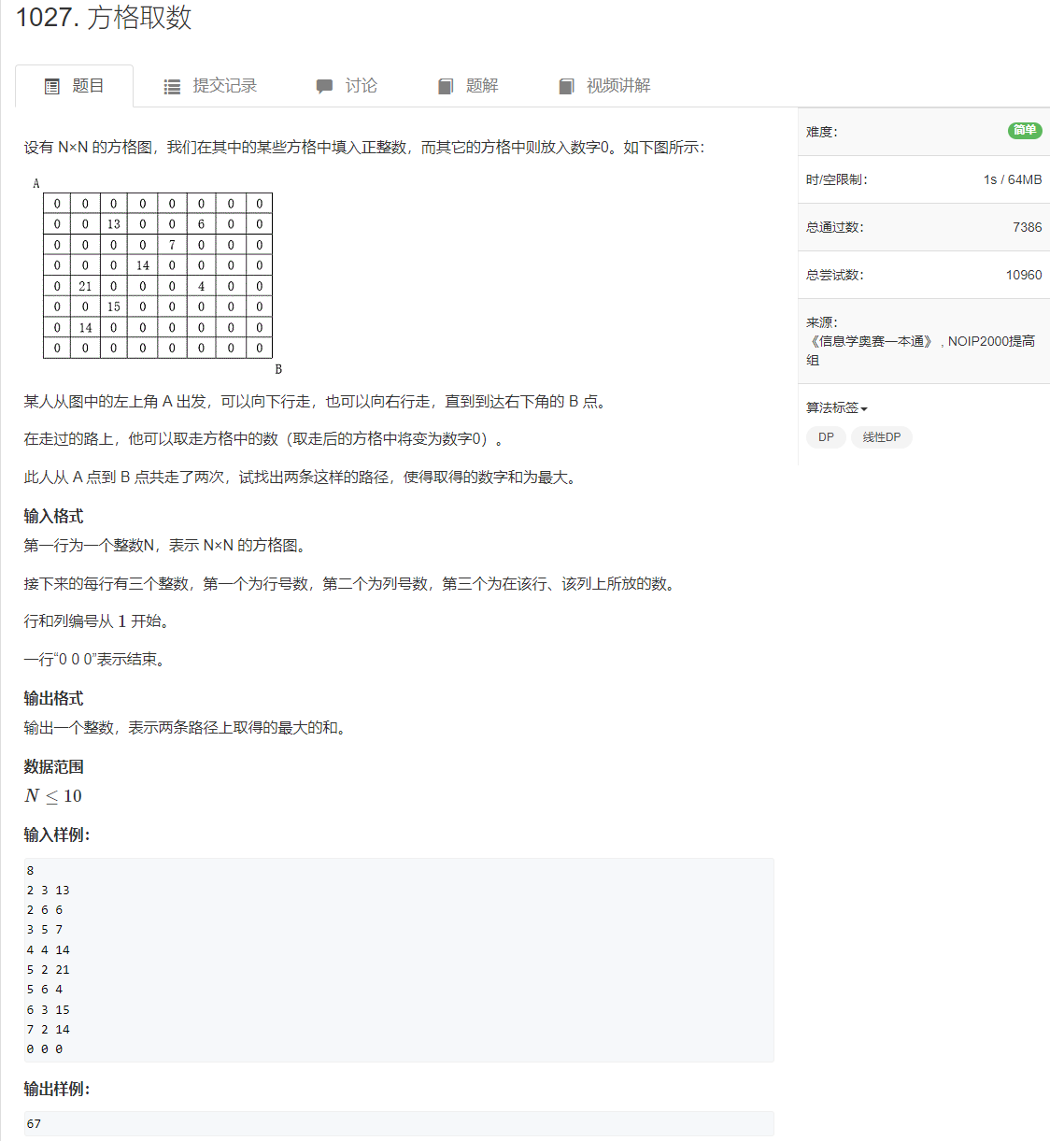
AcWing 1027. Grid access
AcWing 275. Pass note
Where are the imperfections or expression errors in blogging? I hope you can put them forward and the blogger will correct them immediately! I hope you will forgive me
2, AcWing 1015. Picking flowers
1. Title
Link to this question: Flower picking
This blog provides screenshots of this topic:
2. Logical explanation
After we get a topic, we consider it in two steps:
Step 1: abstract the topic: in fact, for a rectangle, we go from the upper left corner to the lower right corner. Each point has a value. After we go to a point, we add the value of this point. We can only go to the right or down each time. If we go to the lower right corner, what is the cumulative maximum value of the value.
Step 2: dp analysis: for example, at [i, j], the key of dp is to analyze which point this point can be converted from: obviously, for this point, it can be converted from one point above or one point on the left according to the meaning of the question, and our demand is the maximum, so we can get the state transition equation:
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
3.AC code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int w[N][N];
int f[N][N];
int main()
{
int t;
cin >> t;
while (t -- )
{
int r, c;
cin >> r >> c;
for (int i = 1; i <= r; i ++ )
for (int j = 1; j <= c; j ++ )
cin >> w[i][j];
for (int i = 1; i <= r; i ++ )
for (int j = 1; j <= c; j ++ )
f[i][j] = max(f[i - 1][j], f[i][j - 1]) + w[i][j];
cout << f[r][c] << endl;
}
return 0;
}
3, AcWing 1018. Minimum toll
1. Title
Link to this question: Minimum toll
This blog provides screenshots of this topic:
2. Logical explanation
After we get a topic, we consider it in two steps:
Step 1: abstract the topic: in fact, for a rectangle, we go from the upper left corner to the lower right corner, and each point has a value. When we go to a point, we add the value of this point. We can only go right or down each time. If we go to the lower right corner, what is the cumulative minimum value of the value.
Step 2: carry out dp analysis: for example, at [i, j], the key of dp is to analyze which point this point can be converted from: obviously, for this point, according to the meaning of the question, it can be converted from one point above or one point on the left. Here you may consider: does the boundary situation require our special judgment? That is, when our i or j is equal to 1, we need special judgment. This problem is different from the previous problem, because our array starts with subscript 1, and because our array is globally defined, the values of points i = 0 and j = 0 are 0 by default, and our demand is the minimum value, so we need special judgment, so we can get the state transition equation:
if (i != 1 && j != 1) f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j]; else if (i == 1) f[i][j] = f[i][j - 1] + w[i][j]; else f[i][j] = f[i - 1][j] + w[i][j];
3.AC code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int w[N][N];
int f[N][N];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
cin >> w[i][j];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i != 1 && j != 1)
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + w[i][j];
else if (i == 1) f[i][j] = f[i][j - 1] + w[i][j];
else f[i][j] = f[i - 1][j] + w[i][j];
cout << f[n][n] << endl;
return 0;
}
4, AcWing 1027. Grid access
1. Title
Link to this question: Grid access
This blog provides screenshots of this topic:
2. Logical explanation
In fact, this question can be regarded as an upgraded version of the first question. We can abstract this question as follows: two people move at the same time according to the rules in one question. Ask the maximum sum after the two people reach the lower right corner. We introduce the Variable k = i1 + j1 = i2 + j2, where k represents the sum of steps taken, and I1 and J1 represent the position of the first person, because only one grid can be moved at a time, Therefore, the total number of steps taken is i1 + j1. Similarly, the second person starts moving at the same time, so there is k = i1 + j1 = i2 + j2. In this question, it is necessary to judge whether the two people are walking in the same grid, that is, whether (i1, j1) and (I2, J2) use the same point. If it is the same point, it is necessary to add a value, otherwise it is necessary to add the value on the two grids
3.AC code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15;
int f[2 * N][N][N];
int w[N][N];
int main()
{
int n;
cin >> n;
int a, b, c;
while (cin >> a >> b >> c, a || b || c)
w[a][b] = c;
for (int k = 2; k <= 2 * n; k ++ )
for (int i1 = 1; i1 <= n; i1 ++ )
for (int i2 = 1; i2 <= n; i2 ++ )
{
int j1 = k - i1, j2 = k - i2;
if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n) //You can't cross the border
{
int &x = f[k][i1][i2];
int t = w[i1][j1];
if (i1 != i2) t += w[i2][j2];
x = max(x, f[k - 1][i1 - 1][i2 - 1] + t); //They all go from top to bottom
x = max(x, f[k - 1][i1][i2] + t); //They all go from left to right
x = max(x, f[k - 1][i1][i2 - 1] + t);
x = max(x, f[k - 1][i1 - 1][i2] + t);
}
}
cout << f[2 * n][n][n] << endl;
return 0;
}
5, AcWing 275. Pass note
1. Title
Link to this question: Pass a note
This blog provides screenshots of this topic:
2. Logical explanation
In this question, we specially stipulate that there can be no intersection. In fact, the starting point is the intersection. Let's judge what to do if there is an intersection:
We still follow the idea of the previous question as two people go from the upper left corner to the lower right corner of the matrix. The two people take one step at the same time, and the two people can't overlap.
Because we stipulate that the two people start at the same time and walk one grid at a time, we must walk to the place where we meet in the path at the same time (note that only the top left corner (initial point) and the bottom right corner (end point) can be walked twice, and other points can only be walked once)
Status representation: f[k, i1, i2] indicates that two people have taken k steps at the same time. The first person is at (i1, k - i1) and the second person is at (i2, k - i2) at this time.
Two people walk to the right at the same time: f[k - 1, i, j] + mark[k, i, j];
Two people walk down at the same time: f[k - 1, i - 1, j - 1] + mark[k, i, j];
The first person goes right and the second person goes down: f[k - 1, i, j - 1] + mark[k, i, j];
The first person goes down and the second person goes right: f[k - 1, i - 1, j] + mark[k, i, j];
3.AC code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 55;
int g[N][N];
int f[2 * N][N][N];
int n, m;
int main()
{
cin >> m >> n;
for (int i = 1; i <= m; i ++ )
for (int j = 1; j <= n; j ++ )
cin >> g[i][j];
for (int k = 2; k <= n + m; k ++ )
for (int i = max(k - n, 1); i <= min(k - 1, m); i ++ )
for (int j = max(k - n, 1); j <= min(k - 1, m); j ++ )
{
if ((i == j) && (k != 2) && (k != n + m)) continue;
int w = g[i][k - i] + g[j][k - j];
for (int a = 0; a <= 1; a ++ )
for (int b = 0; b <= 1; b ++ )
f[k][i][j] = max(f[k][i][j], f[k - 1][i - a][j - b] + w);
}
cout << f[n + m][m][m] << endl;
return 0;
}