Game of oj jumping

Given a nonnegative integer array, assume that your initial position is the first subscript of the array.
Each element in the array represents the maximum length you can jump at that location.
Make sure you can jump to the last subscript of the array.
For example:
A = [2,3,1,1,4],
return true.
A = [3,2,1,0,4],
return false.
Format:
In the first line, enter a positive integer n, and in the next line, enter array A[n]. If you can skip to the last subscript, output "true", otherwise output "false"
Example 1
Input:

5
2 0 2 0 1
Output:
true

Analysis: it is obvious that dfs depth first traversal can solve this problem, but for the case of data volume 500 and the size of each position element in the array, it may time out. So it is necessary to think carefully that dfs will repeat traversal if pruning is not sufficient and time out

Law 1:

#include<iostream>
#include<vector>
#include<algorithm>
#include<iterator>
using namespace std;
int arr[501];
bool flag=0;
int n;
void dfs(int na){//na is the current subscript position 
 if(na>n){
    return;
 }
 if(na==n){
  flag=1;
  return;
 }
 if(arr[na]==0){
    return;
 }
 for(int i=arr[na];i>0;i--){
    if(arr[na]+na>n);
    else{
     dfs(arr[na]+na);   
    }
 } 

}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>arr[i];
    }
        dfs(1);
        if(flag){
            cout<<"true";
        }
        else{
            cout<<"false";
        }

    return 0;
} 

So we came up with a perfect solution of dynamic planning
Law 2:

#include<iostream>
using namespace std;
int arr[501];
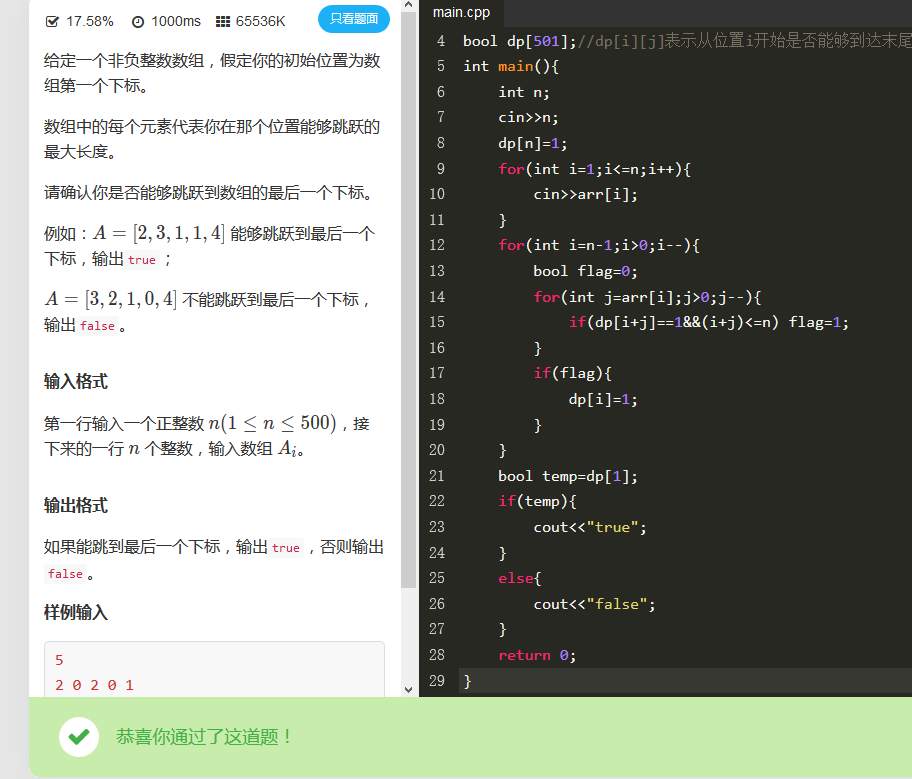
bool dp[501];//dp[i] indicates whether the end can be reached from position I 
int main(){
    int n;
    cin>>n;
    dp[n]=1;
    for(int i=1;i<=n;i++){
        cin>>arr[i];
    }
    for(int i=n-1;i>0;i--){
        bool flag=0;
        for(int j=arr[i];j>0;j--){
            if(dp[i+j]==1&&(i+j)<=n) flag=1;
        }
        if(flag){
            dp[i]=1;
        }   
    }
    bool temp=dp[1]; 
    if(temp){
        cout<<"true";
    }
    else{
        cout<<"false";
    }
    return 0;
}