Dual Graphs and Their Applications

Model

Each planar graph G has a dual planar graph G_
G* has the following properties:

• Each point in G_corresponds to a plane in G_
• For each edge e in G
  
  • e belongs to two faces f1,f2, adding edges (f 1,f 2)
  • e belongs to only one surface f, and add back edge (f f)

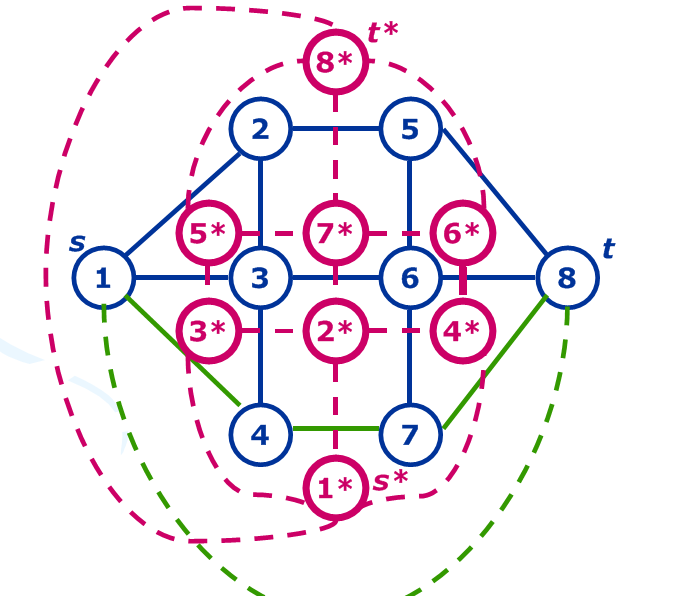
(A green edge enclosed surface is added to the figure, and the edges between s and t need to be deleted.)

So by finding the shortest path from s to t we can find the maximum flow (minimum cut) in the original graph.

Analyse the time complexity:

• Direct Dinic for Maximum Flow: O(EV2)
• Maximum Current Conversion and Shortest Path, Dijkstra: O(Vlog2V) with Reactor Optimization

It's obviously a lot faster, but there's not much difference in actual running.

The main reason is that Dinic's time complexity after optimization is very metaphysical...

subject

[bzoj 1001] Wolf catches rabbits [Bei Jing 2006]

Time Limit: 15 Sec Memory Limit: 162 MB

Topic Description

Now the children's favorite "Pleasant Sheep and Grey Wolf" says that Grey Wolf can't catch sheep, but it's better to catch rabbits.
And now the rabbits are still quite dumb. They only have two nests. Now, as the wolf king, you face the following grid terrain:

The upper left corner is (1,1) and the lower right corner is (N,M) (N=4,M=5 in the figure above). There are three types of roads
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
The weight on the road indicates the maximum number of rabbits that can pass on the road. The road is undirected. The upper left corner and the lower right corner are the two nests of rabbits.
At first all the rabbits gathered in the nest in the upper left corner (1,1). Now they are going to run to the nest in the lower right solution (N,M). The Wolf King begins to ambush.
These rabbits. Of course, for the sake of insurance, if the maximum number of rabbits passing through a road is K, Wolf King needs to arrange for the same number of K wolves.
In order to completely block this road, you need to help Wolf King arrange an ambush plan so that the rabbits can be killed in one net and participate in it.
Wolves are the smallest. Because wolves are going to have trouble with Pleasant Sheep.

Input format

The first behavior N,M. denotes the size of the grid, N,M are less than or equal to 1000.
Next, there are three parts.
The first part consists of N rows, M-1 number per row, representing the weight of the horizontal road.
The second part consists of N-1 rows, the number of M rows per row, representing the weight of the longitudinal road.
In the third part, there are N-1 rows, M-1 number per row, representing the weight of the oblique road.
Enter documents to be guaranteed not to exceed 10M

Output format

Output an integer indicating the minimum number of wolves involved in ambush.

sample input

sample output

This problem is a classical one that converts the maximum flow into the shortest path by using a dual graph.

The idea of solving the problem is very similar to that mentioned before, but it is more difficult to build maps, which needs attention. Another point is that when N=1 or M=1, special judgment is needed.

Maximum flow

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;

const int MAXV=1e6+5,MAXE=3e6+5,INF=~0U>>1;//6

int N,M,S,T;

struct E{int next,to,cap;} e[MAXE<<2];
int ecnt=1,G[MAXV];
void addEdge(int u,int v,int c)
{
    e[++ecnt]=(E){G[u],v,c};G[u]=ecnt;
    e[++ecnt]=(E){G[v],u,0};G[v]=ecnt;
}
int dfn[MAXV];
queue<int> que;
bool calDfn()
{
    int i;
    memset(dfn,-1,sizeof(dfn));
    dfn[S]=0;que.push(S);
    while(!que.empty())
    {
        int u=que.front();que.pop();
        for(i=G[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(e[i].cap>0&&dfn[v]==-1)
                dfn[v]=dfn[u]+1,que.push(v);
        }
    }
    return dfn[T]!=-1;
}
int iter[MAXV];
int calF(int u,int f)
{
    if(u==T) return f;
    for(int & i=iter[u];i;i=e[i].next)
    {
        int v=e[i].to;
        if(e[i].cap>0&&dfn[v]==dfn[u]+1)
        {
            int res=calF(v,min(f,e[i].cap));
            if(res>0)
            {
                e[i].cap-=res,e[i^1].cap+=res;
                return res;
            }
        }
    }
    return 0;
}
int dinic()
{
    int i,f,res=0;
    while(calDfn())
    {
        for(i=1;i<=N*M;i++) iter[i]=G[i];
        while((f=calF(S,INF))>0) res+=f;
    }
    return res;
}
int main()
{
    int i,j,u,v,c;
    scanf("%d%d",&N,&M);
    S=1,T=N*M;
    for(i=1;i<=N;i++)
        for(j=1;j<M;j++)
        {
            u=j+(i-1)*M,v=u+1;scanf("%d",&c);
            addEdge(u,v,c);addEdge(v,u,c);
        }
    for(i=1;i<N;i++)
        for(j=1;j<=M;j++)
        {
            u=j+(i-1)*M,v=u+M;scanf("%d",&c);
            addEdge(u,v,c);addEdge(v,u,c);
        }
    for(i=1;i<N;i++)
        for(j=1;j<M;j++)
        {
            u=j+(i-1)*M,v=u+M+1;scanf("%d",&c);
            addEdge(u,v,c);addEdge(v,u,c);
        }
    printf("%d\n",dinic());
    return 0;
}

shortest path

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;

const int MAXV=2e6+105,MAXE=3e6+5,INF=~0U>>1;

int N,M,S,T;

struct E{int next,to,val;} e[MAXE<<1];int ecnt,G[MAXV];
void addEdge(int u,int v,int w)//Bidirectional side
{
    e[++ecnt]=(E){G[u],v,w};G[u]=ecnt;
    e[++ecnt]=(E){G[v],u,w};G[v]=ecnt;
}

struct HN
{
    int id,v;
    bool operator<(const HN & ot)const
    {return v>ot.v;}
};

priority_queue<HN> heap;
bool inS[MAXV];int dis[MAXV];
int dijkstra()
{
    int i;
    for(i=1;i<=T;i++) dis[i]=INF;
    dis[S]=0;heap.push((HN){S,0});
    while(!heap.empty())
    {
        int u=heap.top().id;heap.pop();
        if(inS[u]) continue;
        inS[u]=true;
        for(i=G[u];i;i=e[i].next)
        {
            int v=e[i].to;
            if(inS[v]) continue;
            if(dis[v]>dis[u]+e[i].val)
            {
                dis[v]=dis[u]+e[i].val;
                heap.push((HN){v,dis[v]});
            }
        }
    }
    return dis[T];
}

int main()
{
    int i,j,w;
    scanf("%d%d",&N,&M);
    if(N==1||M==1)
    {
        if(N>M) swap(N,M);
        int ans=INF;
        for(i=1;i<=M;i++)
            scanf("%d",&w),ans=min(ans,w);
        printf("%d\n",ans);
    }else
    {
        S=2*(N-1)*(M-1)+1,T=S+1;
        //Read Horizontal
        for(i=1;i<M;i++)
        {int v=i*2;scanf("%d",&w);addEdge(S,v,w);}
        for(i=2;i<N;i++)
            for(j=1;j<M;j++)
            {int u=2*((i-2)*(M-1)+j)-1,v=2*((i-1)*(M-1)+j);scanf("%d",&w);addEdge(u,v,w);}
        for(i=1;i<M;i++)
        {int u=2*((N-2)*(M-1)+i)-1;scanf("%d",&w);addEdge(u,T,w);}
        //Read Longitudinal
        for(i=1;i<N;i++)
            for(j=1;j<=M;j++)
            {
                scanf("%d",&w);
                if(j==1)
                {int u=2*((i-1)*(M-1)+j)-1;addEdge(u,T,w);}
                else if(j==M)
                {int v=2*((i-1)*(M-1)+j-1);addEdge(S,v,w);}
                else
                {int u=2*((i-1)*(M-1)+j-1),v=u+1;addEdge(u,v,w);}
            }
        //Read oblique
        for(i=1;i<N;i++)
            for(j=1;j<M;j++)
            {int u=2*((i-1)*(M-1)+j)-1,v=u+1;scanf("%d",&w);addEdge(u,v,w);}
        printf("%d\n",dijkstra());
    }
    return 0;
}
/*
 *  ---------
 *  |1\2|3\4|
 *  |---|---|
 *  |5\6|7\8|
 *  |---|---|
 */