It is known that the three vertex coordinates of a triangle are used to find the circumscribed circle and the circumscribed circle of the triangle.
A triangle has a center of gravity, a center of gravity, a center of gravity, a center of gravity, a center of gravity, a center of gravity, and a center of gravity.
The outer center, the center of an outer circle, is the intersection of three vertical bisectors of a triangle.
Drawing an outer circle is relatively simple.
It is known that the general formulas of the two linear equations are:
a1 * x + b1 * y + c1 = 0
a2 * x + b2 * y + c2 = 0Then, the intersection coordinates are
x = (b2 * c1 - b1 * c2) / (a2 * b1 - a1 * b2) (1)
y = (a1 * c2 - a2 * c1) / (a2 * b1 - a1 * b2) (2)If it is a point skew of two linear equations:
(y - y1) / (x - x1) = k1
(y - y2) / (x - x2) = k2First, turn the point-to-point slant into the general form. You can get it.
a1 = k1, b1 = -1, c1 = y1 - k1 * x1
a2 = k2, b2 = -1, c2 = y2 - k2 * x2Substitute (1), (2) get,
x = (y2 - k2 * x2 - y1 + k1 * x1) / (k1 - k2) (3)
y = (k1 * y2 - k2 * y1 - k1 * k2 * (x2 - x1)) / (k1 - k2) (4)With formulas (3) and (4), it is easy to find the coordinates of the outer center. It's easy to get the midpoint coordinates of the triangle edge. The slope of one is also very good.
Let's set up a triangle. The coordinates of three points are A (x1, y1), B (x2, y2), C (x3, y3).
The midpoint coordinates of edge AB are ((x1 + x2)/2, (y1 + y2)/2), and the slope is (y2 - y1) / (x2 - x1).
The normal of edge AB is perpendicular to AB, and the slope of the normal is (x1 - x2) / (y2 - y1)
The radius of the circumscribed circle is the distance from the center to the vertex
The center of the inner circle is the intersection point of the triangle triangle bisector. It is relatively difficult to find the inner coordinates. The key is that if we find the slope of the angle bisector, we can use the point slope formula, formulas (3) and (4) to get the inner coordinates.
The slope of the angular bisector can be found in this way. For example, to find the slope of the angular bisector of angle A, first find the angle between the vector (A to B) and the x-axis, and then find it.
The angle between the vector (A to C) and the x-axis. The sum of the two angles divided by two is the angle between the angular bisector and the x-axis.
The radius of an inscribed circle needs to be used. The distance formula from a point to a straight line is as follows: 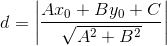
Formula description: The linear equation in the formula is Ax+By+C=0, and the coordinates of point P are (x0,y0).
Code description:
function getAngleWithX_axis(v1, v2)
The angle between the vectors v1 to v2 and the x-axis, and the angle of return is radian.
The angle is calculated by the inverse cosine function, because the logic is the clearest and simplest when implemented by the inverse cosine function. It only needs to judge v2.y >= v1.y.
function getMiddleSlope(a, b, c)
The slope of the angular bisector of the return angle cba. The return angle is radian.
function getCrossPoint(k1, v1, k2, v2)
It is known that the point slopes of two linear equations are obtained, and their intersection coordinates, applications of formulas (3) and (4) are obtained.
function getPointToLineDistance(p, start, end)
It is known that two points on a straight line start and end, a point p outside the line, and the distance from the return point P to the straight line.
<html><head><title>Incircle and circumcircle</title>
</head><body><div>
<canvas id="canvas" width="600" height="450" style="border: solid black 1px; cursor: default;"></canvas>
</div>
<div>
<input type="button" value="clear" onclick="demo.clear();">
<input type="button" value="generate" onclick="demo.generate(1);">
</div>
<script type="text/javascript">
function getRandom(min, max) {
var d = max - min;
return min + Math.random() * d;
}
function getDistance(v1, v2) {
var dx = v2.x - v1.x;
var dy = v2.y - v1.y;
return Math.sqrt(dx * dx + dy * dy);
}
function getAngleWithX_axis(v1, v2) {
var distance = getDistance(v1, v2);
var dx = v2.x - v1.x;
var cosA = dx / distance;
if (v2.y >= v1.y) {
return Math.acos(cosA);
} else {
return 2 * Math.PI - Math.acos(cosA);
}
}
function getMiddleSlope(a, b, c) {
var a1 = getAngleWithX_axis(b, a);
var a2 = getAngleWithX_axis(b, c);
var a3 = (a1 + a2) / 2;
return Math.tan(a3);
}
function getCrossPoint(k1, v1, k2, v2) {
var cross_x = (v2.y - k2 * v2.x - v1.y + k1 * v1.x) / (k1 - k2);
var cross_y = (k1 * v2.y - k2 * v1.y - k1 * k2 * (v2.x - v1.x)) / (k1 - k2);
return new Vertex(cross_x, cross_y);
}
function getPointToLineDistance(p, start, end) {
var a = end.y - start.y;
var b = start.x - end.x;
var c = end.x * start.y - start.x * end.y;
var d = Math.abs(a * p.x + b * p.y + c) / Math.sqrt(a*a + b*b);
return d;
}
function Demo() {
var vertices = [];
var circumcircleCenter;
var circumcircleRadius;
var incircleCenter;
var incircleRadius;
this.generate = function(n) {
var v1 = new Vertex(getRandom(100, 200), getRandom(100, 400));
var v2 = new Vertex(getRandom(200, 400), getRandom(100, 400));
var v3 = new Vertex(getRandom(150, 350), getRandom(100, 400));
vertices.push(v1, v2, v3);
// var kv1 = (v1.y - v2.y) / (v1.x - v2.x);
// var kv2 = (v2.y - v3.y) / (v2.x - v3.x);
var k12 = (v2.x - v1.x) / (v1.y - v2.y);
var k23 = (v3.x - v2.x) / (v2.y - v3.y);
var m12 = new Vertex((v1.x + v2.x)/2, (v1.y + v2.y)/2);
var m23 = new Vertex((v2.x + v3.x)/2, (v2.y + v3.y)/2);
// var circumcircle_x = (m23.y - k23 * m23.x - m12.y + k12 * m12.x) / (k12 - k23);
// var circumcircle_y = (k12 * m23.y - k23 * m12.y - k12 * k23 * (m23.x - m12.x)) / (k12 - k23);
// circumcircleCenter = new Vertex(circumcircle_x, circumcircle_y);
circumcircleCenter = getCrossPoint(k12, m12, k23, m23);
circumcircleRadius = getDistance(circumcircleCenter, v1);
var k213_m = getMiddleSlope(v2, v1, v3);
var k123_m = getMiddleSlope(v1, v2, v3);
incircleCenter = getCrossPoint(k213_m, v1, k123_m, v2);
incircleRadius = getPointToLineDistance(incircleCenter, v1, v2);
this.render();
vertices = [];
};
this.clear = function() {
vertices = [];
this.render();
}
// function render() {
this.render = function() {
var canvas = document.getElementById('canvas');
if (!canvas.getContext)
return;
var context = canvas.getContext('2d');
context.clearRect(0, 0, Number(canvas.width), Number(canvas.height));
if (vertices.length <= 0) {
return;
}
vertices.forEach(function(vertex) {
context.beginPath();
context.arc(vertex.x, vertex.y, 5, 0, Math.PI * 2, true);
context.closePath();
context.fillStyle = "#0000ff";
context.fill();
});
context.beginPath();
context.moveTo(vertices[0].x, vertices[0].y);
for (var i = 1; i < vertices.length; i++) {
context.lineTo(vertices[i].x, vertices[i].y);
}
context.lineTo(vertices[0].x, vertices[0].y);
context.closePath();
context.strokeStyle = "#ff0000";
context.stroke();
//draw circumcircle
drawCircle(context, circumcircleCenter, circumcircleRadius, "#006600");
//draw incircle
drawCircle(context, incircleCenter, incircleRadius, "#990066");
}
};
function drawCircle(ctx, center, radius, centerColor) {
ctx.beginPath();
ctx.arc(center.x, center.y, 5, 0, Math.PI * 2, true);
ctx.closePath();
ctx.fillStyle = centerColor;
ctx.fill();
ctx.beginPath();
ctx.arc(center.x, center.y, radius, 0, Math.PI * 2, true);
ctx.closePath();
ctx.strokeStyle = "#ff0000";
ctx.stroke();
}
function Vertex(x, y) {
this.x = x;
this.y = y;
}
var demo = new Demo();
window.onload = function() {
document.getElementById("canvas").onclick = function(e) {
e = e ? e : window.event;
var rect = this.getBoundingClientRect();
demo.addAt(e.clientX - rect.left, e.clientY - rect.top);
}
};
</script>
</body></html>