summary

Divide and conquer (D & C) algorithm is a classical recursive method to solve problems. Divide and conquer is its main idea.
Applicable scenarios:
1) Find the termination condition (baseline condition) and stop recursion. The simpler the condition, the better;
2) It can decompose the problem and continuously reduce the scale of the problem until the termination conditions are met.
Quick sorting is a classical sorting algorithm based on divide and conquer idea.
Talk is cheap, show me code.
Several simple small examples will be used to help understand, all of which are implemented in python.

Example 1

Sum arrays, for example x = [1, 3, 2, 6, 5,7, 7, 9, 0, 0, 8], sum(x)=48 

First, consider whether to reduce the scale of the problem. Array x contains multiple elements. The summation operation is an accumulation operation, which always adds two elements. Then the whole array can be decomposed into multiple addition of two elements. At this time, the minimum scale of the problem is the addition of two elements;
Then, considering the termination conditions, in addition to containing multiple elements, array X may be an empty array or an element. If it is an empty array, and is 0, the array containing one element, and is x[0].

def dc_sum(num_list):
	if len(num_list) == 0:  # Termination conditions
	    return 0
	elif len(num_list) == 1: # Termination conditions
	    return num_list[0]
	else:
	    return num_list[0] + dc_sum(num_list[1:]) # Reduce the scale of the problem

Example 2

Find the maximum value of the array, for example x = [1, 3, 2, 6, 5,7, 7, 9, 0, 0, 8], max(x)=9

Similar to summation, the maximum can be decomposed into the comparison between two elements, and the termination conditions are the same.

def dc_max(num_list):
	if len(num_list) == 0:  # Termination conditions
	    return 0
	elif len(num_list) == 1: # Termination conditions
	    return num_list[0]
	else:
		# Reduce the scale of the problem
		tmp1 = num_list[0]
		tmp2 = dc_max(num_list[1:])
		if tmp1 > tmp2
			return tmp1
		else:
			return tmp2

Example 3

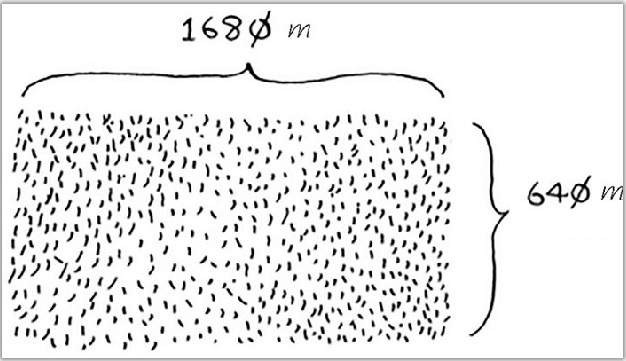
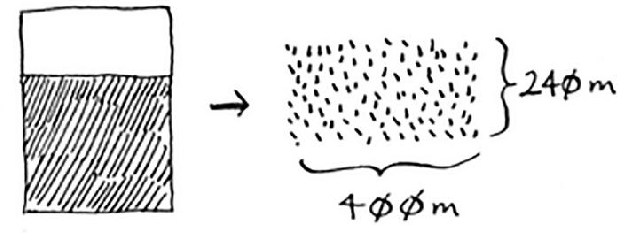
A piece of land needs to be evenly divided into blocks. The blocks to be divided shall be as large as possible and the maximum side length of the block shall be calculated. The land is as follows:

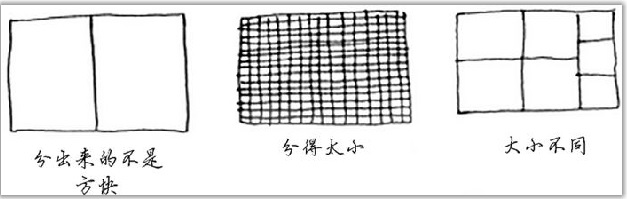
The title is required to be square and as large as possible, so the division shown in the figure below is unreasonable:

Suppose that a piece of land is 25x25, then what meets the conditions is such a division of 25x25. If it is 50x25, what meets the conditions is to divide two 25x25 areas, that is, find a box whose length and width can be divided as much as possible, so as to ensure that the divided box is as large as possible.
But the width and height of the land given in the title can not be divided. What should we do?
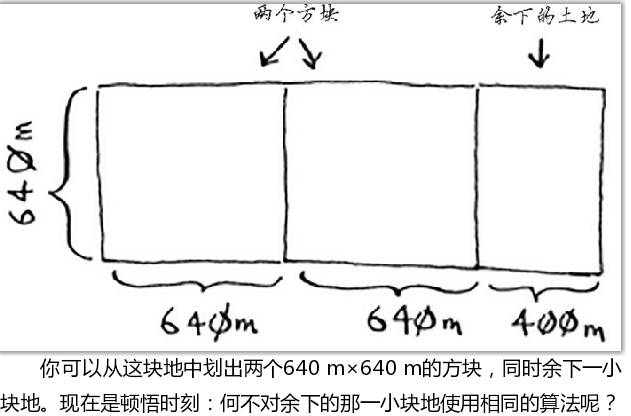
Two 640x640 areas can be divided from the land, and one piece of land is left at the same time. For the rest of the land, use the same method to divide the land with the shortest side as the block, and then the rest of the land again. Cycle this operation until a land with length and width that can be divided is found.

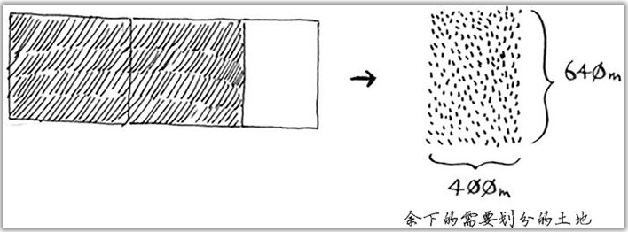
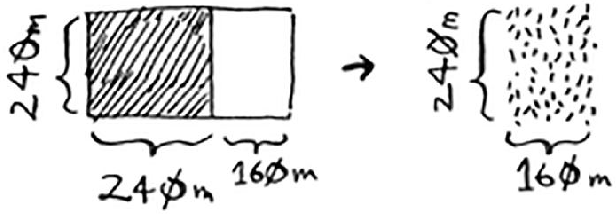
def dc_land_split(height, width):
	max_len = max(height, width)
	min_len = min(height, width)
	if max_len%min_len == 0: # Termination conditions
		return min_len
	else:
		# Reduce the scale of the problem
	    return dc_land_split(max_len%min_len, min_len) 

Quick sort

Quick sorting algorithm is one of the classical sorting algorithms, and its average running time is O ( n l o g n ) O(nlogn) O(nlogn), the worst case is O ( n 2 ) O(n^2) O(n2).
Steps:
1) Select a reference value (pivot);
2) Divide the remaining elements in the array into two arrays. Those less than pivot are placed in one array, those greater than pivot are placed in another array, and those equal to pivot are placed in any array, so that pivot is in the middle of the original array.
3) Repeat 2) to sort the two arrays respectively.

The above step 2) is actually a process of reducing the scale, gradually decomposing the original array into multiple small arrays, and sorting is realized in the decomposition process.
The termination condition is that the number of elements in the array is less than 2.

def quick_sort(num_list):
	if len(num_list) < 2:
		return num_list
	
	# pivot = num_list[0]
	pivot = num_list[len(num_list)//2]
	num_list.pop(len(num_list)//2)
	less = []
	greater = []
	for i in num_list:
		if i < pivot:
			less.append(i)
		else:
			greater.append(i)
	less = quick_sort(less)
	greater = quick_sort(greater)
	return less + [pivot] + greater

When taking pivot, if the first element is removed as the benchmark value, the worst case is to perform a fast sorting operation on the sorted array. Then there is always a sub array that is an empty array, and its call stack is O ( n ) O(n) O(n), run time O ( n 2 ) O(n^2) O(n2), if the middle element of the array is taken, its call stack is O ( l o g n ) O(logn) O(logn), running time O ( n l o g n ) O(nlogn) O(nlogn).