Accuracy

Different from the accuracy rate below, the accuracy rate is the total number of all prediction pairs divided by the total number, which is equivalent to the proportion of finding the correct prediction.

Accuracy

For our prediction results, it shows how many of the samples predicted to be positive are real positive samples. Then there are two possibilities to predict a positive class: one is to predict a positive class as a positive class (TP), the other is to predict a negative class as a positive class (FP), that is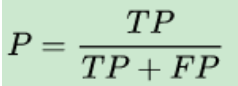

recall

That is to find the correct proportion in the positive category.
For our original sample, it shows how many positive examples in the sample are predicted correctly. There are two possibilities, one is to predict the original positive class as a positive class (TP), the other is to predict the original positive class as a negative class (FN).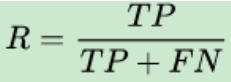

F1 SCORE

F1 score can be regarded as a kind of harmonic average of model accuracy rate and recall rate. Its maximum value is 1 and its minimum value is 0.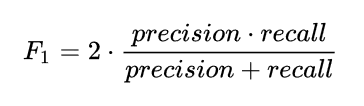

Confusion matrix

In machine learning, especially in statistical classification, confusion matrix is also called error matrix.
Each column of the matrix represents the classifier's class prediction for the sample, and each row of the matrix represents the real class to which the version belongs

It is called "confusion matrix" because it is easy to see whether machine learning has confused the categories of samples.

Here's an example: consider 0 as a positive class and 1 as a negative class. (Ref https://blog.csdn.net/rocling/article/details/97139901)

sklearn has these corresponding encapsulation functions.
What should be noted is the corresponding interpretation of average: "macro", "micro", "weighted", "None" code

import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
print(accuracy_score(y_true, y_pred))  # 0.5
print(accuracy_score(y_true, y_pred, normalize=False))  # 2

# In the case of multi label classification with binary label indicator
print(accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2))))  # 0.5

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
print(precision_score(y_true, y_pred, average='macro'))  # 0.2222222222222222
print(precision_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(precision_score(y_true, y_pred, average='weighted'))  # 0.2222222222222222
print(precision_score(y_true, y_pred, average=None))  # [0.66666667 0.         0.        ]


print(recall_score(y_true, y_pred, average='macro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='weighted'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average=None))  # [1. 0. 0.]

print(f1_score(y_true, y_pred, average='macro'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(f1_score(y_true, y_pred, average='weighted'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average=None))  # [0.8 0.  0. ]

If None is selected, the scores of each category will be output directly without weighting.

Macro Average macro average means that each category has the same weight when calculating the mean value, and the final result is the arithmetic average of the indicators of each category. (category average)
Micro Average

Micro average is to give the same weight to each sample of all categories when calculating multi category indicators, and to combine all samples to calculate each indicator. (sample average)

weighted is based directly on the weight.

P-R curve

To evaluate the quality of a model, we can not only rely on the accuracy or recall rate. It is better to build multiple groups of accuracy and recall rates, and draw the P-R curve of the model.
Let's talk about the drawing method of P-R curve. The horizontal axis of the P-R curve is the recall rate, and the vertical axis is the accuracy rate. A point on the P-R curve represents that under a certain threshold value, the model will determine the result larger than the threshold value as a positive sample, and the result smaller than the threshold value as a negative sample. At this time, the recall rate and accuracy rate corresponding to the returned result will be returned. The whole P-R curve is generated by moving the threshold from high to low. Near the origin represents the accuracy and recall rate of the model when the threshold value is maximum. (Reference: https://blog.csdn.net/hfutdog/article/details/88085878)