Most of us may know BFS and DFS better. For Dijkstra algorithm, it is the algorithm to solve the single source shortest path problem in the graph algorithm structure.
It is probably such a weighted graph. Dijkstra algorithm can calculate the shortest path from any node to other nodes. (single source shortest path problem), Dijkstra algorithm can only find the shortest distance from one vertex to other points, not any two points.
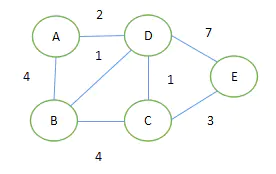
First, let's review the basis of graph theory,
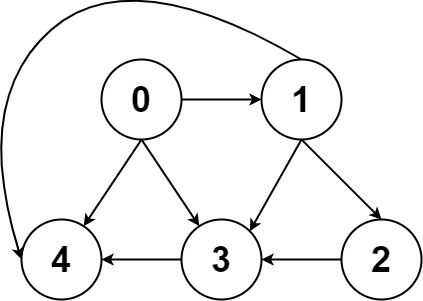
A graph is composed of nodes and edges. The logical structure is as follows. We usually use adjacency table or adjacency matrix to realize it:
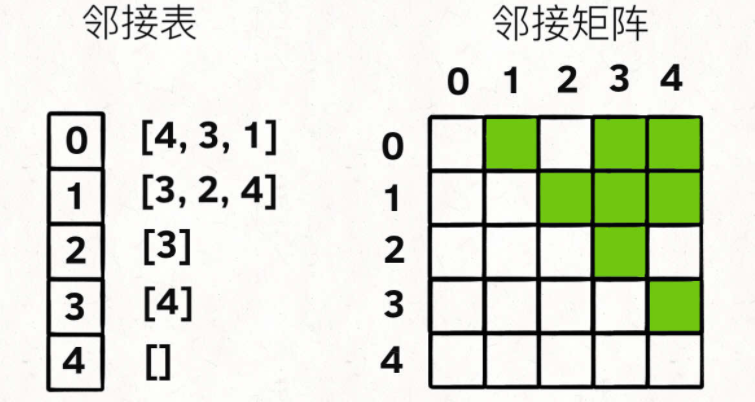
① The adjacency table is very intuitive. I save the neighbors of each node X in a list, and then associate x with this list, so that all its adjacent nodes can be found through a node X.
② The adjacency matrix is a two-dimensional Boolean array. We call it a matrix. If nodes X and y are connected, set matrix[x][y] to true (the green square in the figure above represents true). If you want to find a neighbor of node x, just scan matrix[x] [...].
Advantages and disadvantages:
For adjacency tables, the advantage is that they occupy less space. However, the adjacency table cannot quickly judge whether two nodes are adjacent.
For example, I want to judge whether node 1 is adjacent to node 3. I want to find out whether 3 exists in the neighbor list corresponding to node 1 in the adjacency table. But the adjacency matrix is simple. Just look at matrix[1][3], which is efficient.
Implementation of directed weighted graph
If it is an adjacency table, we store not only all neighbor nodes of a node x, but also the weight of X to each neighbor.
If it is an adjacency matrix, matrix[x][y] is no longer a Boolean value, but an int value. 0 indicates no connection, and other values indicate weight.
How to implement undirected graph
If you connect nodes X and Y in an undirected graph, you can change matrix[x][y] and matrix[y][x] to true; Adjacency table is a similar operation.
Traversal of Graphs
The biggest difference between a graph and a multitree is that a graph may contain rings. You may traverse from a node of the graph and return to this node after a circle. Therefore, if the graph contains rings, the traversal framework needs a visited array for assistance;
boolean[] visited;
/* Graph traversal framework */
void traverse(Graph graph, int s) {
if (visited[s]) return;
// Pass node s
visited[s] = true;
for (int neighbor : graph.neighbors(s))
traverse(graph, neighbor);
// Leave node s
visited[s] = false;
}
The operation of this visited array is very similar to that of the backtracking algorithm for "making selection" and "canceling selection". The difference lies in the position. The "making selection" and "canceling selection" of the backtracking algorithm are inside the for loop, while the operation of the visited array is outside the for loop.
1. Binary tree level traversal and BFS algorithm

// Enter the root node of a binary tree and traverse the binary tree
void levelTraverse(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
// Traverse each layer of the binary tree from top to bottom
while (!q.isEmpty()) {
int sz = q.size();
// Traverse each node of each layer from left to right
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
printf("node %s In the first %s layer", cur, depth);
// Put the next level node in the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}
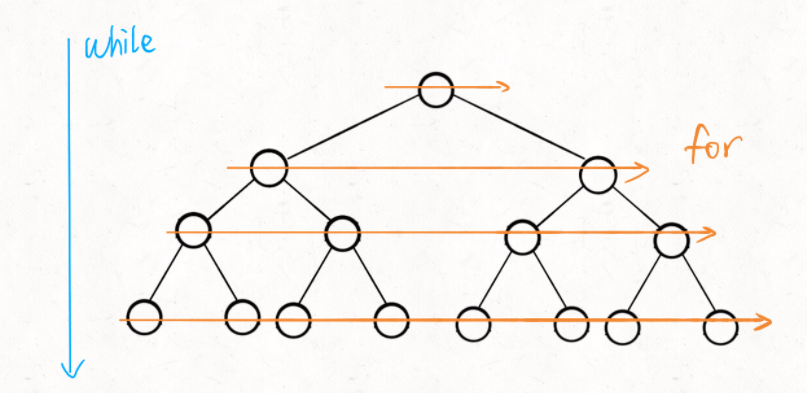
The while loop controls layer by layer to go down, and the for loop uses sz variables to control traversing the binary tree nodes of each layer from left to right.
Note that the depth variable in our code framework actually records the number of layers currently traversed. In other words, whenever we traverse a node cur, we know which layer this node belongs to.
2. Based on the traversal framework of binary tree, we can extend the sequence traversal framework of multi binary tree:
// Enter the root node of a multi tree and traverse the multi tree
void levelTraverse(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
// Traverse each layer of the multitree from top to bottom
while (!q.isEmpty()) {
int sz = q.size();
// Traverse each node of each layer from left to right
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
printf("node %s In the first %s layer", cur, depth);
// Put the next level node in the queue
for (TreeNode child : cur.children) {
q.offer(child);
}
}
depth++;
}
}
Based on the traversal framework of multi fork tree, we can extend the algorithm framework of BFS (breadth first search):
// Enter the starting point for BFS search
int BFS(Node start) {
Queue<Node> q; // Core data structure
Set<Node> visited; // Avoid going back
q.offer(start); // Add starting point to queue
visited.add(start);
int step = 0; // Record the number of search steps
while (q not empty) {
int sz = q.size();
/* Spread all nodes in the current queue one step around */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
printf("from %s reach %s What is the shortest distance %s", start, cur, step);
/* Add the adjacent nodes of cur to the queue */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
step++;
}
}
Based on the traversal framework of multi tree, we can extend the algorithm framework of BFS (breadth first search). The so-called BFS algorithm is to abstract the algorithm problem into a "no right graph", and then continue to play the set of binary tree level traversal
// Enter the starting point for BFS search
int BFS(Node start) {
Queue<Node> q; // Core data structure
Set<Node> visited; // Avoid going back
q.offer(start); // Add starting point to queue
visited.add(start);
int step = 0; // Record the number of search steps
while (q not empty) {
int sz = q.size();
/* Spread all nodes in the current queue one step around */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
printf("from %s reach %s What is the shortest distance %s", start, cur, step);
/* Add the adjacent nodes of cur to the queue */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
step++;
}
}
This is the application of weighted graph, so we can't use it for weighted graph, because the shortest path problem of weighted graph is not judged according to the number of steps. So we need to further simplify the framework and remove the for in the while loop.
// Enter the root node of a binary tree and traverse all nodes of the binary tree
void levelTraverse(TreeNode root) {
if (root == null) return 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// Traverse each node of the binary tree
while (!q.isEmpty()) {
TreeNode cur = q.poll();
printf("I don't know %s On which floor", cur);
// Put child nodes in queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
If you want to maintain the depth variable at the same time and let each node cur know its layer, you can think of other methods, such as creating a new State class and recording the number of layers of each node:
class State {
// Record the depth of the node
int depth;
TreeNode node;
State(TreeNode node, int depth) {
this.depth = depth;
this.node = node;
}
}
// Enter the root node of a binary tree and traverse all nodes of the binary tree
void levelTraverse(TreeNode root) {
if (root == null) return 0;
Queue<State> q = new LinkedList<>();
q.offer(new State(root, 1));
// Traverse each node of the binary tree
while (!q.isEmpty()) {
State cur = q.poll();
TreeNode cur_node = cur.node;
int cur_depth = cur.depth;
printf("node %s In the first %s layer", cur_node, cur_depth);
// Put child nodes in queue
if (cur_node.left != null) {
q.offer(new State(cur_node.left, cur_depth + 1));
}
if (cur_node.right != null) {
q.offer(new State(cur_node.right, cur_depth + 1));
}
}
}
Dijkstra algorithm framework
We also need State to assist in the execution of the algorithm
class State {
// id of the graph node
int id;
// Distance from start node to current node
int distFromStart;
State(int id, int distFromStart) {
this.id = id;
this.distFromStart = distFromStart;
}
}
Similar to the sequence traversal of the binary tree just now, we also need to use the State class to record some additional information, that is, use the distFromStart variable to record the distance from the starting point start to the current node.
The Dijkstra algorithm in the weighted graph is different from the ordinary BFS algorithm in the weighted graph. In the Dijkstra algorithm, the path weight when you pass a node for the first time is not necessarily the smallest. Therefore, for the same node, we may go through multiple times, and each distFromStart may be different, such as the following figure:
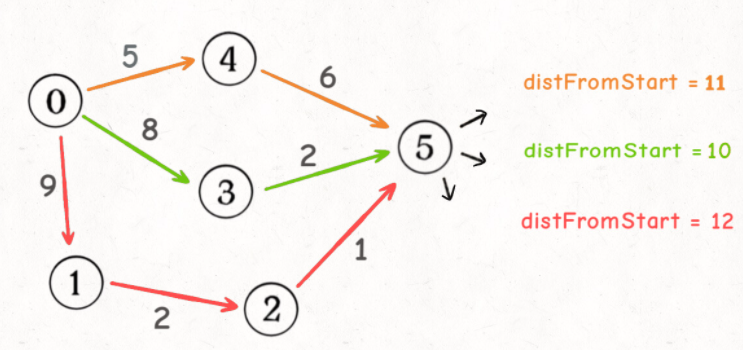
I will pass through node 5 three times, and the distFromStart value of each time is different. Then I take the smallest distFromStart, which is the weight of the shortest path from the starting point start to node 5
The framework is as follows:
// Returns the weight of the edge from node from to node to
int weight(int from, int to);
// Input node s returns the adjacent nodes of S
List<Integer> adj(int s);
// Enter a graph and a start point to calculate the shortest distance from start to other nodes
int[] dijkstra(int start, List<Integer>[] graph) {
// Number of nodes in the graph
int V = graph.length;
// Record the weight of the shortest path. You can understand it as dp table
// Definition: the value of distTo[i] is the weight of the shortest path from node start to node I
int[] distTo = new int[V];
// Find the minimum value, so dp table is initialized to positive infinity
Arrays.fill(distTo, Integer.MAX_VALUE);
// base case, the shortest distance from start to start is 0
distTo[start] = 0;
// Priority queue: the smaller distFromStart is in the front
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distFromStart - b.distFromStart;
});
// Start BFS from start
pq.offer(new State(start, 0));
while (!pq.isEmpty()) {
State curState = pq.poll();
int curNodeID = curState.id;
int curDistFromStart = curState.distFromStart;
if (curDistFromStart > distTo[curNodeID]) {
// There is already a shorter path to the curNode node
continue;
}
// Load the adjacent nodes of curNode into the queue
for (int nextNodeID : adj(curNodeID)) {
// See if the distance from curNode to nextNode will be shorter
int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
if (distTo[nextNodeID] > distToNextNode) {
// Update dp table
distTo[nextNodeID] = distToNextNode;
// Put the node and distance into the queue
pq.offer(new State(nextNodeID, distToNextNode));
}
}
}
return distTo;
}