Dig a Bessel Curve and those things
I. Past and present life
Bessel Curve was originally designed to serve industrial design, especially for applications and automotive curve design. With the wide application of computer drawing, it is not easy to draw smooth and accurate curves on the computer. Bessel curve solves such a problem. Bessel dashed line determines the beginning and end of the curve by starting point and ending point, and determines the direction of the curve by several control points. Because it is widely popularized by French Engineer Pierre Bessel, the curve is named Bessel curve.
2. Mathematical Foundation
Arbitrary continuous curves on the plane can be approximated by Bernstein polynomials, so when we want to draw a curve in the plane, if we can simulate the function of the curve, we can precisely control the computer to draw a series of points on the curve to draw the curve. Bessel curve is based on such a mathematical basis.
First of all, for a Bessel curve, the three elements are: starting point, ending point and control point. The starting point of the curve is at the starting point, the end point is at the end point, the curve does not pass through the control point, the control point to grasp the direction of the curve, the number of control points can be uncertain.
1. First-order Bessel Curve
The number of control points of the first order Bessel curve is 0, only the starting and ending points. In fact, the first-order Bessel curve is a straight line segment from the starting point to the end point. The formula is as follows:
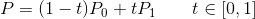
In the above formula, P is the point on the curve, P0 is the starting point, P1 is the ending point. (For points on the plane, the x and y coordinates can be calculated by the above formulas respectively). Because of its linear formula, all such Bessel curves are also called first-order Bessel curves. The following figure can well describe the drawing process of line segments when t changes from 0 to 1:

2. Second order Bessel curve
The second-order Bessel curve has a control point, assuming the starting point, the control point and the end point are P 0, P 1 and P 2, respectively. Connect P0P1, P1P2, between 0-1, take point M on P0P1 line segment and point N on P1P2 line segment, make P0M/P0P1=P1N/P1P2, find a point Q on line segment MN, and make MQ/QN=P0M/P0P1=P1N/P1P2, the set of all Q points is Bessel curve. The above description is somewhat abstract. It is clear by mathematical deduction. The formulas are as follows:
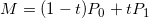
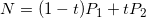
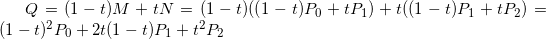
The drawing process is as follows:

3. Higher order Bessel curve
With the foundation of first and second order, higher order Bessel curves are derived in the same way. A general recursive formula is as follows:
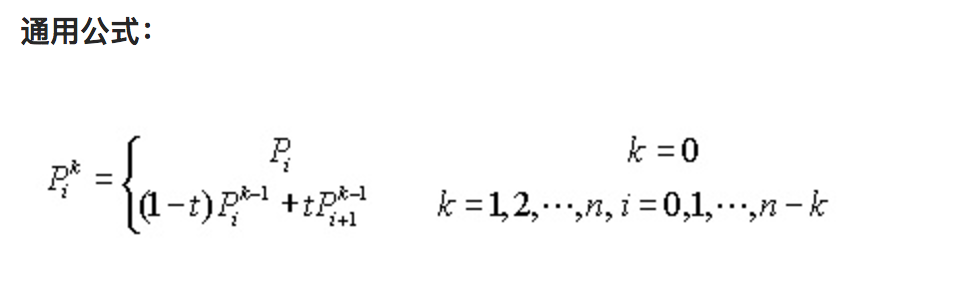
The third and fourth order rendering processes are illustrated as follows:

3. Application of Bessel Curve in iOS
Although Bessel curve is very easy to implement in many areas of development, because I am familiar with iOS development, and the above example of curve drawing is also achieved through iOS program. This paper briefly discusses the application of Bessel curve in iOS. Firstly, CGPath is provided in the core graphics framework of CoreGraphics, which can directly create Bessel curve. The Bessel curve function supported by the system has two and three orders. There is a blog discussion in front of me. I won't repeat it here. The address is as follows:
https://my.oschina.net/u/2340880/blog/757072.
Here are the UIBezierPath classes in the UIKit framework.
//Construction method + (instancetype)bezierPath; //Constructing with Rectangles + (instancetype)bezierPathWithRect:(CGRect)rect; //Construct with rounded rectangle + (instancetype)bezierPathWithOvalInRect:(CGRect)rect; //Create rounded rectangular Bessel paths and set rounded radius + (instancetype)bezierPathWithRoundedRect:(CGRect)rect cornerRadius:(CGFloat)cornerRadius; + (instancetype)bezierPathWithRoundedRect:(CGRect)rect byRoundingCorners:(UIRectCorner)corners cornerRadii:(CGSize)cornerRadii; //Create with an arc + (instancetype)bezierPathWithArcCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise; //Create with CGPath + (instancetype)bezierPathWithCGPath:(CGPathRef)CGPath; //CGPath object @property(nonatomic) CGPathRef CGPath; //Move the path to a point - (void)moveToPoint:(CGPoint)point; //Add a day line - (void)addLineToPoint:(CGPoint)point; //Adding a second-order Bessel curve segment - (void)addCurveToPoint:(CGPoint)endPoint controlPoint1:(CGPoint)controlPoint1 controlPoint2:(CGPoint)controlPoint2; //Add a third-order Bessel curve segment - (void)addQuadCurveToPoint:(CGPoint)endPoint controlPoint:(CGPoint)controlPoint; //Add arc - (void)addArcWithCenter:(CGPoint)center radius:(CGFloat)radius startAngle:(CGFloat)startAngle endAngle:(CGFloat)endAngle clockwise:(BOOL)clockwise; //Closing path - (void)closePath; //Remove all points - (void)removeAllPoints; //Add a path - (void)appendPath:(UIBezierPath *)bezierPath; //Reverse the path - (UIBezierPath *)bezierPathByReversingPath; //transform - (void)applyTransform:(CGAffineTransform)transform; //Is the path empty? @property(readonly,getter=isEmpty) BOOL empty; //size @property(nonatomic,readonly) CGRect bounds; //Current point @property(nonatomic,readonly) CGPoint currentPoint; //Determine whether a point is included - (BOOL)containsPoint:(CGPoint)point; //Set line width @property(nonatomic) CGFloat lineWidth; //Setting the style of wire cap @property(nonatomic) CGLineCap lineCapStyle; //Setting up a Breakpoint Style @property(nonatomic) CGLineJoin lineJoinStyle; @property(nonatomic) CGFloat miterLimit; @property(nonatomic) CGFloat flatness; //Parity rule @property(nonatomic) BOOL usesEvenOddFillRule; //Make dotted line settings - (void)setLineDash:(nullable const CGFloat *)pattern count:(NSInteger)count phase:(CGFloat)phase; - (void)getLineDash:(nullable CGFloat *)pattern count:(nullable NSInteger *)count phase:(nullable CGFloat *)phase; //Fill-in drawing - (void)fill; //Carry out path drawing - (void)stroke;
IV. Examples
Following is a Demo demo of iOS platform, which can dynamically draw Bessel curve and observe the auxiliary line and drawing process. It can flexibly configure the drawing speed and control points:

The Github address is as follows: