Logu Title Link

loj End Title Link

Topic:

Play a chess game on one axis.Chess pieces can only be placed on the whole point.No more than one piece can be placed at each point.Complete with Chess: There are 3 pieces on the board, in the three positions a, b and c.We want to move their positions to x, y, z with the least jumps.

Rule of Jump: Select any piece and jump against a centre-axis piece.The distance between the two pieces does not change after the jump.Only one piece is allowed to be skipped at a time.If you can complete the output YES and the required number of steps, you can do so without outputting NO.

Yes, only one chess piece is allowed to skip (because this has been thinking for a long time about being autistic)

After reading the title, the first reaction was: woc, what does it have to do with LCA?Where's this tree from??

That's right (%dalao)

Classified discussions reveal that there are only three possible scenarios for each legal state (i.e. no coincidence of chess pieces).

1. Midpoint (y) jumps to the left

2. Midpoint (y) Jump to Right

3.Jump left (or right) to the middle=>It can be demonstrated that since only one piece can be skipped, only one can be taken at d1!=d2

It looks like a binary tree?(1.2 as a child node, 3 as a father node)

For case 1.2, we can see (take 1 as an example below):

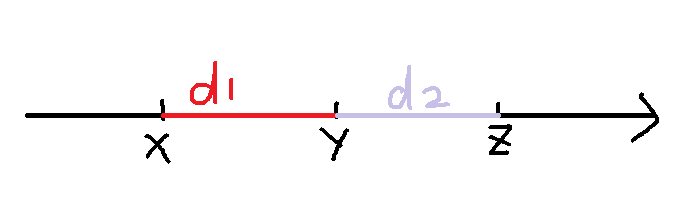
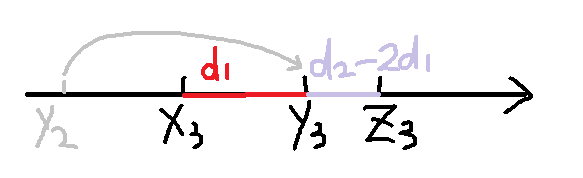
As you know, the left chess piece can't jump when D1 > d2. We can take step d2/d1 at most. At this time, step D2 is less than D1 and takes a different direction. When d2%d1 equals 0, step d2/d1-1 will reach the root.

So from this, we can figure out the ancestors of the start and end states and determine if their ancestors are equal=>because the same ancestors can be obtained by doing the opposite

This is a simulation. We can use division to speed up jumps ((jumps time out one by one)

Simulation section:

 1                 int d1=y-x;
 2         int d2=z-y;
 3         if(d1<d2)
 4         {
 5             int step=d2/d1;
 6             if(d2%d1==0)    step--;
 7             if(step>dis)    step=dis;
 8             x+=step*d1;
 9             y+=step*d1;
10             if(x>y)    swap(x,y);
11             dis-=step;
12         }
13         else
14         {
15             int step=d1/d2;
16             if(d1%d2==0)    step--;
17             if(step>dis)    step=dis;
18             z-=d2*step;
19             y-=d2*step;
20             if(z<y)    swap(z,y);
21             dis-=step;
22         }        

Once a common ancestor is found, you can divide the search (find the number of steps to jump up)

l is 0, r is min (distance from common ancestor, starting point from common ancestor)

1                 int l=0,r=min(dep1,dep2),step=0;
2             while(l<=r)
3         {
4             int mid=l+r>>1;
5             b1=go(st,mid);
6             b2=go(ed,mid);
7             if(pd(b1,b2))    step=mid,r=mid-1;
8             else    l=mid+1;
9         }      

That's what I think is the core content (perceptual understanding without understanding it)

  1 #include<iostream>
  2 #include<cstdio>
  3 using namespace std;
  4 struct node{
  5     int x,y,z;
  6 }st,ed,b1,b2;
  7 int dep1,dep2;
  8 inline int read(){
  9     char ch;
 10     int sign=1;
 11     while((ch=getchar())<'0'||ch>'9')
 12         if(ch=='-')    sign=-1;
 13     int res=ch-'0';
 14     while((ch=getchar())>='0'&&ch<='9')
 15         res=res*10+ch-'0';
 16     return res*sign;
 17 }
 18 inline void sort(node &x){
 19     if(x.x>x.y)    swap(x.x,x.y);
 20     if(x.x>x.z)    swap(x.x,x.z);
 21     if(x.y>x.z)    swap(x.y,x.z);
 22 }
 23 inline int findfather(node &b){
 24     int res=0;
 25     sort(b);
 26     while(b.x+b.z!=b.y*2)
 27     {
 28         int d1=b.y-b.x;
 29         int d2=b.z-b.y;
 30         if(d1<d2)
 31         {
 32             int step=d2/d1;
 33             if(d2%d1==0)    step--;
 34             b.x+=step*d1;
 35             b.y+=step*d1;
 36             if(b.x>b.y)    swap(b.x,b.y);
 37             res+=step;
 38         }
 39         else
 40         {
 41             int step=d1/d2;
 42             if(d1%d2==0)    step--;
 43             b.z-=step*d2;
 44             b.y-=step*d2;
 45             if(b.y>b.z)    swap(b.y,b.z);
 46             res+=step;
 47         }
 48     }
 49     return res;
 50 }
 51 inline bool pd(node x,node y){
 52     if(x.x==y.x&&x.y==y.y&&x.z==y.z)    return true;
 53     return false;
 54 }
 55 inline int abs(int x){
 56     return x>=0?x:-x;
 57 }
 58 inline node go(node b,int dis){
 59     sort(b);
 60     while(dis)
 61     {
 62         int d1=b.y-b.x;
 63         int d2=b.z-b.y;
 64         if(d1<d2)
 65         {
 66             int step=d2/d1;
 67             if(d2%d1==0)    step--;
 68             if(step>dis)    step=dis;
 69             b.x+=step*d1;
 70             b.y+=step*d1;
 71             if(b.x>b.y)    swap(b.x,b.y);
 72             dis-=step;
 73         }
 74         else
 75         {
 76             int step=d1/d2;
 77             if(d1%d2==0)    step--;
 78             if(step>dis)    step=dis;
 79             b.z-=d2*step;
 80             b.y-=d2*step;
 81             if(b.z<b.y)    swap(b.z,b.y);
 82             dis-=step;
 83         }
 84     }
 85     return b;
 86 }
 87 int main(){
 88     st.x=read();st.y=read();st.z=read();
 89     ed.x=read();ed.y=read();ed.z=read();
 90     sort(st);sort(ed);
 91     b1=st;b2=ed;
 92     dep1=findfather(b1);
 93     dep2=findfather(b2);
 94     if(!pd(b1,b2))
 95     {
 96         printf("NO\n");
 97         return 0;
 98     }
 99     else
100     {
101         int c=abs(dep1-dep2);
102         if(dep1<dep2)
103             ed=go(ed,c);
104         else if(dep1>dep2)
105             st=go(st,c);
106         int l=0,r=min(dep1,dep2),step=0;
107         while(l<=r)
108         {
109             int mid=l+r>>1;
110             b1=go(st,mid);
111             b2=go(ed,mid);
112             if(pd(b1,b2))    step=mid,r=mid-1;
113             else    l=mid+1;
114         }
115         printf("YES\n");
116         printf("%d",step*2+c);
117     }
118     return 0;
119 }