First, the dictionary tree: https://blog.csdn.net/forever_dreams/article/details/81009580 Big Boys Blog
Also known as word search tree, Trie tree It is a kind of tree structure It's a variant of a hash tree. Typical applications are used for statistics, sorting and saving large quantities. character Strings (but not limited to strings) are often used in text word frequency statistics by search engine systems. Its advantages are: using common prefixes of strings to reduce query time, minimizing unnecessary string comparison, and making query more efficient than hash tree. Its basic operations are: find, insert and delete, of course, delete operations are relatively rare. Baidu entry
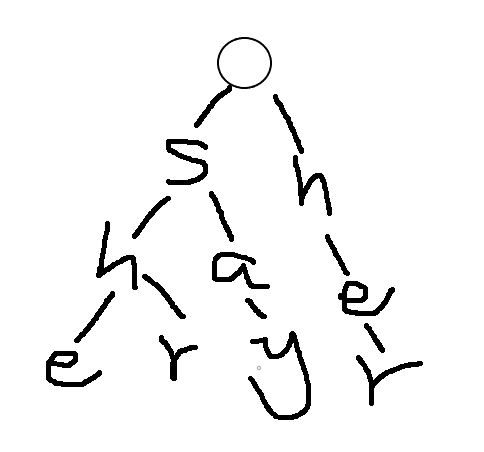
A dictionary tree inserting strings she, he, say, shr, her is
Next is the basic operation:
1. insertion
Or the picture above.
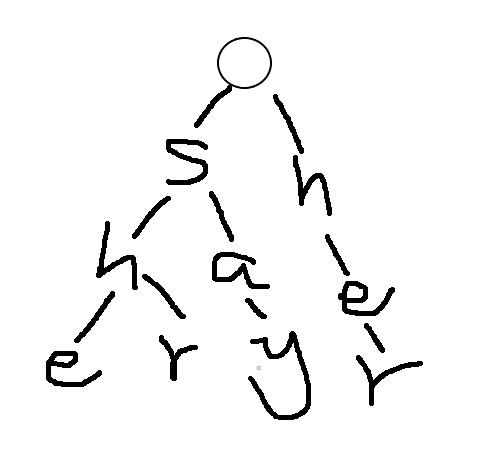
First, the root node must not have characters.
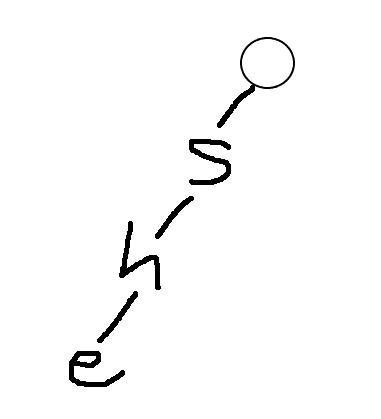
Then let's start inserting. First, s h E. We find that the root node's sub-nodes do not have s and can be inserted. The sub-nodes of s do not have h and can be inserted. The sub-nodes of H do not have e and can be inserted. Then that's it.
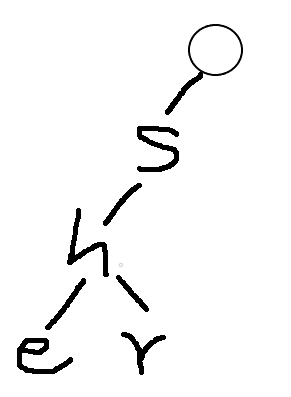
When we insert shr, we find that the root node's sub-nodes exist s, so we can share the node with him and remember the word share.
Continue to insert h, find that the sub-node of s already exists h, so we can continue to share, and finally insert r, we find that the sub-node of H does not exist r, so we can insert
Become so
Have you found any nature?
1. When we insert it, we insert it from the next layer of the root node, that is, the child node.
2. Before inserting a string, check whether the same character exists in this layer, share if it exists, and create a new child node if it does not exist.
void bulid_trie(){
int len=s.length();
int idx=0;//Current letter number
for(int i=0;i<len;++i){
if(star[idx].son[s[i]-'a']==0){//This node does not exist
star[idx].son[s[i]-'a']=++flag;//So create a new node
}
idx=star[idx].son[s[i]-'a'];//Update the location to insert the next node
}
}2. query
Query operations are similar to insertion, except that no new child nodes are needed.
For example, when we query her, the letters are numbered 1, 2, 3, respectively.
Starting from the root node, if the child node of the root node exists s, update the number (1) whose current location is s. Continue to find whether the child node of s exists h, exists, and updates the location. Continue to find whether the child node of H exists e, exists, updates the location. Then find that the string query is completed, exit the loop body, and the query ends. .
The following code records that this string was queried several times during the query
int query(){
int len=s.length();
int idx=0;//Current letter number
for(int i=0;i<len;++i){
//The absence of this letter indicates that the word does not exist, so return 0
if(star[idx].son[s[i]-'a']==0)
return 0;
idx=star[idx].son[s[i]-'a'];
}
star[idx].num++;//The word has been queried several times.
return star[idx].num++;
}For example, the question P2580, so he mistakenly began the roll call. https://www.luogu.org/problem/P2580
#include<iostream>
#include<cstring>
#include<math.h>
#include<stdlib.h>
#include<cstring>
#include<cstdio>
#include<utility>
#include<algorithm>
#include<map>
using namespace std;
typedef long long ll;
inline int read(){
int X=0,w=0;char ch=0;
while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
return w?-X:X;
}
/*------------------------------------------------------------------------*/
const int maxn=1e6;
struct node{
int num;//Number of occurrences after the word's end traverses
int son[26];
}star[maxn*10];
int n,m;
string s;
int flag;
void bulid_trie(){
int len=s.length();
int idx=0;//Current letter number
for(int i=0;i<len;++i){
if(star[idx].son[s[i]-'a']==0){//This node does not exist
star[idx].son[s[i]-'a']=++flag;//So create a new node
}
idx=star[idx].son[s[i]-'a'];//Update the location to insert the next node
}
}
int query(){
int len=s.length();
int idx=0;//Current letter number
for(int i=0;i<len;++i){
//The absence of this letter indicates that the word does not exist, so return 0
if(star[idx].son[s[i]-'a']==0)
return 0;
idx=star[idx].son[s[i]-'a'];
}
star[idx].num++;//The word has been queried several times.
return star[idx].num++;
}
int main()
{
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
//Each letter has its own number.
cin>>n;
for(int i=1;i<=n;++i){
cin>>s;
bulid_trie();
}
cin>>m;
for(int i=1;i<=m;++i){
cin>>s;
int ans=query();
if(ans==1) printf("OK\n");
if(ans==0) printf("WRONG\n");
if(ans>1) printf("REPEAT\n");
}
return 0;
}Complexity: Trie tree is a space-for-time algorithm. It takes a lot of space, but time is very efficient. The time complexity of insertion and query is O(1).