The reason for writing this article is that after embedding with SVD and deepwall in a recommended task, the effect of the model has been improved, and the application of SVD is beyond the knowledge of dimension reduction and there is a lot to think about, so some methods of SVD and embedding are summarized.
1. Singular Value Decomposition SVD
1.1 SVD Dimension Reduction
SVD decomposes a matrix, assuming A is a
m
×
n
m\times n
A matrix of m x n, then
X
X
The SVD of X is:
X
=
U
∑
V
T
X = U\sum V^T
X=U∑VT
among U U U is a matrix of threes. ∑ \sum _is a matrix of x_which is zero except for the elements on the principal diagonal. Each element on the principal diagonal is called a singular value, and V is a matrix of X. U U U and V V V are unitary matrices, that is, they satisfy: 𝑈 T 𝑈 = 𝐼 , 𝑉 T 𝑉 = 𝐼 𝑈^T𝑈=𝐼,𝑉 ^ T𝑉=𝐼 UTU=I,VTV=I
In singular matrices ( ∑ \sum Singular value (diagonal element)In many cases, the sum of the first 10% or even 1% of the singular values accounts for more than 99% of the total singular values, so it can be thought that the first 10% or even 1% of the singular values contain 99% of the total singular value information. Then the maximum k singular values and corresponding left and right singular vectors can be used to approximate the description.Describe the matrix, that is:
X m × n = U m × m ∑ m × n V n × n T ≈ U m × k ∑ k × k V k × n T X_{m\times\ n} = U_{m\times m} \sum_{m\times n}V_{n\times n}^T\approx U_{m\times k}\sum_{k\times k}V_{k\times n}^T Xm× n=Um×mm×n∑Vn×nT≈Um×kk×k∑Vk×nT
Where k is much smaller than n, that is, a large matrix A can be used with three small matrices U m × k , ∑ k × k , V k × n T U_{m\times k} ,\sum_{k\times k},V_{k\times n}^T Um x k, k x k, Vk x nT are expressed, so SVD can be used to reduce dimensionality, process data compression and de-drying.
1.2 word embedding based on SVD
Singular value decomposition works by first traversing the dataset through a matrix X X X stores the number of co-occurrences (co-occurrence matrix) of a word, and then decomposes X into singular values. U U The row value of U can be used as word embedding for all words in the glossary.
For example, there are three sentences in a dataset with a window size of 1:
1. I enjoy flying. 2. I like NLP. 3. I like deep learning.
The co-occurrence matrix is:
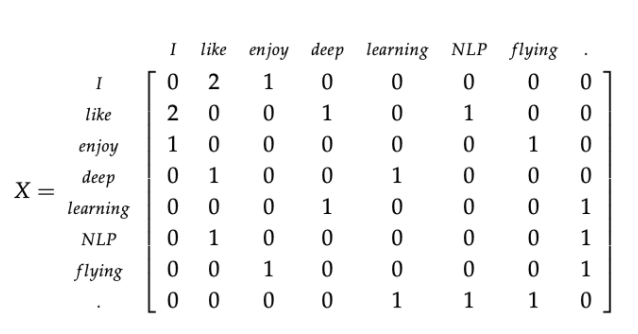
Using SVD, X = U ∑ V T X=U∑V^T X=U_VT, select the first k dimensions of U to get the k-dimensional word vector. Although this method has some drawbacks, it also represents a word through the context distribution instead of the isolated''exclusive'''. The co-occurrence matrix can also be replaced by tf-idf matrix, and then reduced by SVD.
Although word vectors are obtained, the interpretation of word vectors by matrix decomposition is not very well understood, so to explore further, first look at the structure of Word2vec:
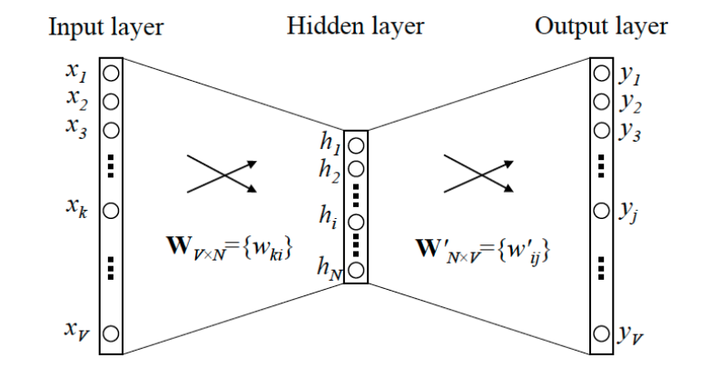
Without considering the activation function, this is a three-layer neural network with N intermediate nodes and V output. Y = X W W T Y=XWW^T Y=XWWT This formula is very similar to the formula of SVD, exactly like skip-gram, where the input of skip-gram can be seen as the sum of multiple one-hot s and the input, and each row in the coexistence matrix in SVD has the same structure. So it can be simply considered that the two structures are the same, except Word2Vec can be seen as predicting the current word from the front and back words, while self-encoder or SVD can be used to predict the current word.Predict the word before and after by the word before and after; and Word2Vec is followed by softmax to predict the probability, that is, a non-linear transformation is implemented, but SVD does not.
Of course, there are other shortcomings in SVD compared with word2vec except that they have not undergone non-linear transformation:
(1) The size of the repository changes when new words are added (unk or incremental training can be used to solve this problem in word2vec).
(2) The matrix is too sparse and most words do not appear at the same time.
(3) High matrix dimension ( ≈ 1 0 6 × 1 0 6 \approx10^6\times10^6 _106 x 106), high training cost ( O ( m n 2 ) O(mn^2) O(mn2) )
SVD in 1.3 Recommendation System
SVD in the recommendation system, which we are familiar with, is the case of movie ratings. Scores in the matrix represent how much users like movies, most of which are missing data.
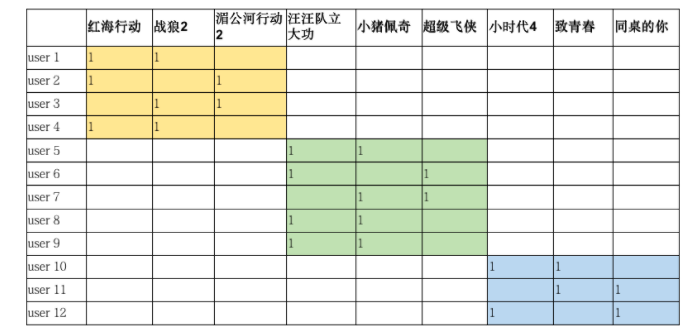
This is a sparse matrix, where the score matrix is counted as X. The elements indicate user's score on item. Many of them are missing and need to be predicted. Finally, the top K movies with the highest predicted score are recommended to the user. First, the SVD formula can be used by X = U ∑ V T X = U\sum V^T X=U_VT is simplified to make Z = U ∑ , Y = V T Z = U\sum,Y=V^T Z=U, Y=VT, so for score matrix X, it can be expressed as the product of two matrices Z and Y:
X m × n = Z m × k Y k × n X_{m\times\ n} = Z_{m\times k} Y_{k\times n} Xm× n=Zm×kYk×n
Where m is the number of user s and n is the number of item s, you can see that the score matrix has been decomposed into two matrices, a more visual representation:
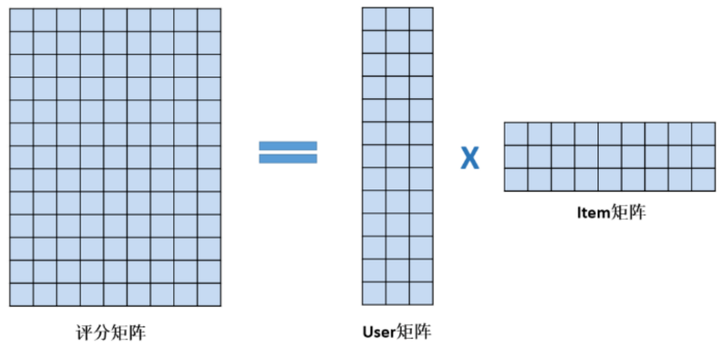
Scoring matrices are known, and after breaking them into two matrices, each user's rating for each type of movie (the type is constructed to explain the underlying characteristics between the movies) and for each type of movie.
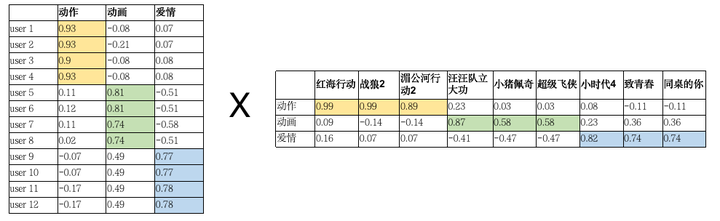
Predictive rating of movie i by a user uEqual to the product of the User and Item vectors, so you can get a predictive rating for each movie by each user, but must the rating be reliable? This can be compared against known data and predictions from the original rating table. If the difference is large, will this decomposition be useless? There is already a taste of deep learning here.With predicted and true values, the data inside the user and item can be updated using a continuously optimized method to make the predicted and true results close. Here the loss function can be RMSE, MAE, etc. The larger the score value in the final scoring table, the more likely the user will like the movie, the more valuable the movie will be recommended to the user.
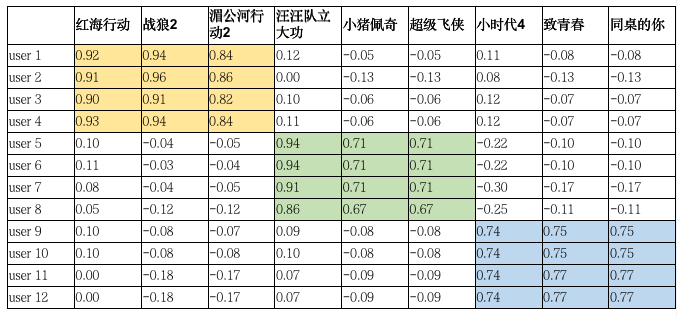
In effect, SVD is a clustering of movie types of rating matrices. For the user matrix, you can see that users are clustered, and for the item matrix, you can see that each movie is clustered. Multiplication of the matrix, you can see that users and movies match.
1.4 embedding based on SVD
The three roles of SVD have been described above, and the role of SVD that I use in my recommendation task can be thought of as clustering. In the recommendation task, there are userid (user id), feedid (video id), and so on, which are illustrated with these two examples. Our goal is to explore the potential relationship between users and different videos. It is also simpler to construct a co-occurrence matrix of the two features first.
import datatable as dt
from tqdm import tqdm
from scipy.sparse import lil_matrix, csr_matrix
def build_inter_matrix(path, row_item, col_item, row_vocab, col_vocab):
total_df = dt.fread(path).to_pandas()
matrix = lil_matrix((len(row_vocab), len(col_vocab)), dtype=np.float32)
for _, row in tqdm(total_df.iterrows(), total=len(total_df), desc=f'Building {row_item}-{col_item} matrix'):
row_val = row[row_item]
if col_item == 'feedid':
col_val = row[col_item]
else:
col_val = feed_dict[row['feedid']][col_item]
matrix[row_vocab[row_val], col_vocab[col_val]] += 1.0
return matrix.tocsr()
Where path is the dataset path, in the example row_item='userid', col_item='feedid', row_vocab is each id corresponding to token in userid (e.g. user A has an id of 1, user B has a id of 2),col_vocab is each id corresponding to token in feedid (e.g., video x1 has an id of 1, video x2 has a id of 2).To save memory, the co-occurrence matrix is saved in a sparse matrix. By decomposing the co-occurrence matrix into two matrices, the vectors corresponding to the userid and the feedid can be obtained. One of the vectors in the userid can be seen as a mapping relationship between the user and different videos (e.g. liking level)A vector in the feed id can be seen as a mapping relationship between the video and different users, which can be used as a variable to enter the model and also solve the cold start problem.
from functools import partia
#To speed up, multiple processes are utilized.
func = partial(build_inter_matrix, row_item='userid', col_item='feedid',
row_vocab=user_token2id, col_vocab=feed_token2id)
uid_fid_sparse = parallelize(user_df, func)
u_SVD_vector, f_SVD_vector = SVD(uid_fid_sparse, dim=64)
from multiprocessing import cpu_count, Pool, Manage
def parallelize(df, func):
part = 10 #cpu_count() // 2
data_split = np.array_split(df, part)
if not os.path.exists(os.path.join(TRAIN_TEST_DATA_PATH, 'user_act_part0.csv')):
data_path = []
for i, part_data in tqdm(enumerate(data_split), desc='split data'):
part_path = os.path.join(TRAIN_TEST_DATA_PATH, f'user_act_part{i}.csv')
part_data.to_csv(part_path, index=False, encoding='utf8')
data_path.append(part_path)
else:
data_path = [os.path.join(TRAIN_TEST_DATA_PATH, path) for path in os.listdir(TRAIN_TEST_DATA_PATH) if 'user_act' in path]
pool = Pool(part)
data = sum(pool.map(func, data_path))
pool.close()
pool.join()
return data
2.TFIDF-SVD
This part of internal use comes from WeChat Big Data Contest Trick - How to 0.706+on 3ID ,This is just to distinguish it from the above methods. Or use userid and feedid as examples to find video-based user reproducibility. If some video users are always present together, then it is likely that these users have the same hobbies, they will most likely be forwarded together, commented on, and watched together through TFIDF.Get:
userid,feedid Two vectors; groupby(userid)[feedid).agg(list); groupby(feedid)[userid).agg(list);
This is grouped according to userids and then put the feedid s together to build the video vector characteristics for each user. If you don't understand this, imagine userid as an article, feed ID as text, and use tfidf to get the vector.
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.decomposition import TruncatedSVD
def tfidf_SVD(data, f1, f2, n_components=100):
n_components = 100
tmp = data.groupby(f1, as_index=False)[f2].agg({'list': lambda x: ' '.join(list(x.astype('str')))})
tfidf = TfidfVectorizer(max_df=0.95, min_df=3, sublinear_tf=True)
res = tfidf.fit_transform(tmp['list'])
print('SVD start')
SVD = TruncatedSVD(n_components=n_components, random_state=2021)
SVD_res = SVD.fit_transform(res)
print('SVD finished')
for i in (range(n_components)):
tmp['{}_{}_tfidf_SVD_{}'.format(f1, f2, i)] = SVD_res[:, i]
tmp['{}_{}_tfidf_SVD_{}'.format(f1, f2, i)] = tmp['{}_{}_tfidf_SVD_{}'.format(f1, f2, i)].astype(np.float32)
del tmp['list']
return tmp
def get_first_SVD_features(f1_, n_components = 100):
# userid_id_dic: User's mapping dictionary;
# First_cls_dic [f1_]: mapping dictionary for f1;
f1_embedding_userid = pd.DataFrame({f1_:list(first_cls_dic[f1_].values())})
f1_embedding_userid_tmp = tfidf_SVD(df_train_val[[f1_, 'userid']], f1_, 'userid', n_components)
f1_embedding_userid = f1_embedding_userid.merge(f1_embedding_userid_tmp, on = f1_, how = 'left')
f1_embedding_userid = f1_embedding_userid.fillna(0)
f1_embedding_userid = f1_embedding_userid[[c for c in f1_embedding_userid.columns if c not in [f1_]]].values
np.save(embedding_path + '{}_embedding_userid.npy'.format(f1_),f1_embedding_userid)
del f1_embedding_userid,f1_embedding_userid_tmp
gc.collect()
userid_embedding_f1 = pd.DataFrame({'userid':list(userid_id_dic.values())})
userid_embedding_f1_tmp = tfidf_SVD(df_train_val[['userid', f1_]], 'userid', f1_, n_components)
userid_embedding_f1 = userid_embedding_f1.merge(userid_embedding_f1_tmp, on = 'userid', how = 'left')
userid_embedding_f1 = userid_embedding_f1.fillna(0)
userid_embedding_f1 = userid_embedding_f1[[c for c in userid_embedding_f1.columns if c not in ['userid']]].values
np.save(embedding_path + 'userid_embedding_{}.npy'.format(f1_),userid_embedding_f1)
del userid_embedding_f1,userid_embedding_f1_tmp
gc.collect()
get_first_SVD_features('feedid')
get_first_SVD_features('authorid')
TFIDF-SVD embedding and SVD embedding are operations that simply replace the co-occurrence matrix with a matrix composed of TFIDF, but there are differences in nature.
1) TFIDF-SVD method is to first use TFIDF operation to get user vector features, but the dimension is too large. The purpose of using SVD is to reduce the dimension. In the embedding method of SVD, SVD can be regarded as playing a clustering role.
2) From the result, TFIDF-SVD only uses the first vector after decomposition, that is, it uses the X = U ∑ V T X = U\sum V^T The U vector in X=U_VT is used as the eigenvector, while the SVD embedding method uses the U U Sum of U vectors V T V^T VT is the eigenvector.
3.deepwalk
Depwalk (2014) is a random walk method to simulate the relationship between any two variables. Its main idea is to random walk on the graph structure consisting of items, generate a large number of item sequences, then input these item sequences as training samples into word2vec to get embedding of items. The whole DeepWalk algorithm process can be divided into four steps:
1) Show the original sequence of user behavior
2) Item-related diagrams are constructed based on these user behavior sequences
def build_graph(df, graph, f1, f2):
for item in df[[f1, f2]].values:
if isinstance(item[1], str):
if not item[1]: continue
for token in item[1].split(';'):
graph['item_' + token].add('user_' + str(item[0]))
graph['user_' + str(item[0])].add('item_' + token)
else:
graph['item_' + str(item[1])].add('user_' + str(item[0]))
graph['user_' + str(item[0])].add('item_' + str(item[1]))
3) Select the starting point randomly by random walk to regenerate the item sequence.
4) Finally, these item sequences are input into the word2vec model to generate the Embedding vector of the final item.
def deepwalk(train_df, test_df, f1, f2, flag, emb_size):
print("deepwalk:", f1, f2)
print('Building graph ...')
graph = defaultdict(set)
build_graph(train_df, graph, f1, f2)
build_graph(test_df, graph, f1, f2)
# print('graph:',graph)
print("Creating corpus ...")
path_length = 10
sentences = []
length = []
keys = graph.keys()
for key in tqdm(keys, total=len(keys), desc='Walk'):
sentence = [key]
while len(sentence) != path_length:
key = random.sample(graph[sentence[-1]], 1)[0]
if len(sentence) >= 2 and key == sentence[-2]:
break
else:
sentence.append(key)
sentences.append(sentence)
length.append(len(sentence))
if len(sentences) % 100000 == 0:
print(len(sentences))
print(f'Mean sentences length: {np.mean(length)}')
print(f'Total {len(sentences)} sentences ...')
print('Training word2vec ...')
random.shuffle(sentences)
model = Word2Vec(sentences, vector_size=emb_size, window=4, min_count=1, sg=1, workers=10, epochs=20)
print('Outputing ...')
values = np.unique(np.concatenate([np.unique(train_df[f1]), np.unique(test_df[f1])], axis=0))
w2v = {}
for v in tqdm(values):
if 'user_' + str(v) not in model.wv:
vec = np.zeros(emb_size)
else:
vec = model.wv['user_' + str(v)]
w2v[v] = vec
pickle.dump(
w2v,
open('./data/wedata/deepwalk/' + f1 + '_' + f2 + '_' + f1 + '_' + flag + '_deepwalk_' + str(emb_size) + '.pkl',
'wb')
)
if 'list' in f2:
values = [items.split(';') for items in train_df[f2].values] + [items.split(';') for items in
test_df[f2].values]
values = set([token for v in values for token in v])
else:
values = np.unique(np.concatenate([np.unique(train_df[f2]), np.unique(test_df[f2])], axis=0))
w2v = {}
for v in tqdm(values):
if 'item_' + str(v) not in model.wv:
vec = np.zeros(emb_size)
else:
vec = model.wv['item_' + str(v)]
w2v[v] = vec
print(list(w2v.items())[:5])
pickle.dump(
w2v,
open('./data/wedata/deepwalk/' + f1 + '_' + f2 + '_' + f2 + '_' + flag + '_deepwalk_' + str(emb_size) + '.pkl',
'wb')
)
deepwalk(train, test, 'userid', 'feedid', 'dev', 64)
Because a user's representation of the video is randomly simulated, this embedding can be solved even if a cold boot occurs.
4. Summary
This paper summarizes the various applications of SVD and the applications of TFIDF-SVD and DeepWalk in embedding. The main functions of SVD are dimensionality reduction, word embedding and clustering.Like TFIDF-SVD and DeepWalk, embedding can be used in the case of userid and feedid, which not only solves the cold startup problem, but also represents the hidden relationship between user and feed very well. I hope it can be a reference for you whether it is the role of SVD or the centralized embedding method.
Reference resources
1.Detailed application of SVD in recommendation system and algorithm derivation
2.Principle of Singular Value Decomposition (SVD) and Its Application in Dimension Reduction
3.word2vec Learning Compilation (SVD, Principle Derivation)
4.Summary of embedding technology
5. Sujianlin.(Jan. 15, 2017).SVD Decomposition (1): Self-Encoder and Artificial Intelligence [Blog post].Retrieved fromhttps://spaces.ac.cn/archives/4208
6. Sujianlin.(Feb. 23, 2017).SVD Decomposition (3): Even Word2Vec is just a SVD? [Blog post].Retrieved fromhttps://spaces.ac.cn/archives/4233
7.WeChat Big Data Contest Trick - How to 0.706+on 3ID
8.[Graph Embedding] DeepWalk: Algorithmic principles, implementation and Application