network flow

Recently, in learning binary graph matching, network flow and game theory (% eazy,miaomiao,lsr_dalao,zyh,zlt), thank you guys for giving the lecture to the burdock, which has benefited me a lot. PPT will not be put on. There are copyright issues. Now let me talk about my recent experience in learning network flow. (Thanks to ergeda and the careful counseling of brains and buttocks for the progress of colds the other day.) Smile and spit your tongue

what is network flow???

According to the ppt of lsr_dalao:
Definition:
In graph theory, a theory and method is used to study a class of optimization problems on networks.
Many systems involve traffic flow problems, such as traffic flow in highway system, data information flow in network, oil flow in oil supply pipeline, etc. We can further understand the directed graph as a "flow network" and use such an abstract model to solve traffic problems.
Obviously, I don't understand it, so I'll use what human beings can understand. For example, we have a transportation network as follows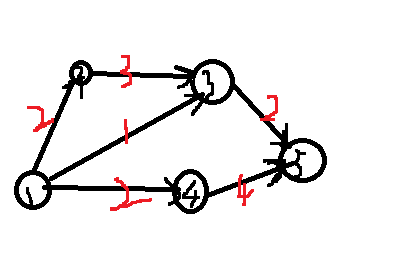
It's a bit ugly, but just put up with it. QAQ. Let's assume that one point is Changsha, five points is Beijing, and two, three and four points are Wuhan, Zhengzhou and Shijiazhuang, respectively. Suppose we go north by train. We can only take two people on the train from Changsha to Wuhan (by analogy). We don't change journeys and get off the train. How many elegant students from Changsha can get to Beijing? Obviously, there are four people.
The following picture: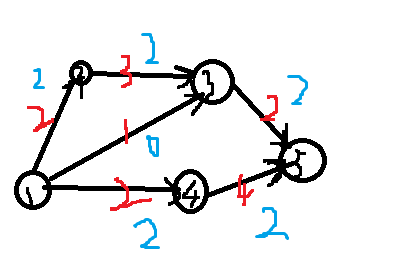

The blue number represents the maximum number of people on the train. Why is 1 - > 3 0? Because we're asking for the largest number of people, well, that's it.

2. Introduce the method and code of maximum flow of network flow.

Still quote lsr_dalao's ppt Chinese first
1. introduction
The basic idea of solving network flow is to find an augmented path every time (that is, a feasible path from source to sink point) and then ans+= augment the flow that can flow through the road, update the remaining network, and then do augmented path until no augmented path can be made. The most difficult thing to understand about the introduction of network flow is the remaining network.... Why after finding an augmented road... not only should the feasible traffic on each side be subtracted from the traffic that the augmented road may flow through... but also the reverse arc on each side plus the traffic that the augmented road may flow through... The reason is that the augmented road may be blocked when doing the augmented road... or the augmented road would have been a smooth one. Ordered to find the maximum flow... But we are arbitrary... In order to correct.... each time the flow is added to the reverse arc... So that the flow can self-adjust... The remaining network updates (just update on the original map)............................ speak earth language!) Anyway, I didn't understand... If there is a God around, don't spray.
Next, let's talk about the simplest and slowest EK of the maximum network flow. algorithm:
Let's set the traffic network we just had as graph G. This graph is a directed graph. Otherwise, we can't do it. Remember this sentence. There's a title behind it. Define the c function as the capacity of the pipeline, that is, how many people can sit on the train at most, and the f function as the flow of the pipeline, that is, how many people are doing on the train now.
Obviously, the c function is larger than or equal to the size of the F function (not to mention, more water will burst the pipe, and secondly, this is China, not India, or can not ride on the top of the train). This is one of the three properties of graph G: capacity limitation, and then there is an antisymmetry, that is, f = f flowing back. Now I don't know. When I talk about the reverse side, I will talk about it in detail. The third is the conservation of flow, that is, the total flow from the source point is equal to the total flow from the sink point, that is, the elegant ladies from Changsha can't disappear on the train.
With that in mind, I'm now going to talk about the hardest thing to understand in network traffic: the reverse side.
Here's a classic picture: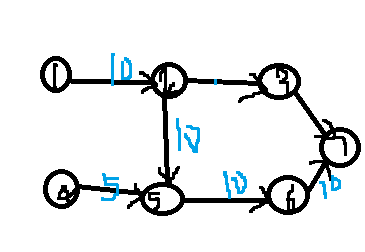

It's still ugly. Well, digraph, let's not say much. Initially, the flow of node 0 to node 1 and node 4 (not drawn) is 10. Let's assume that the path is full, that is, c = f can't flow to other flows. Then we set the flow of C = 10, 4 - > 5 on the other side as well, if according to the bfs of EK algorithm, in order to Find a maximum flow, 2 - > 3 side will not go, may initially find the bottleneck to enter the team 4,5, but the flow is adjusted back to 10, after all, the program is to find the maximum flow, so if you do not add a reverse side 4 - > 5 this flow will not be added to the augmented road, you may not understand, I will first introduce the residual network. Luo, so you will understand more deeply.

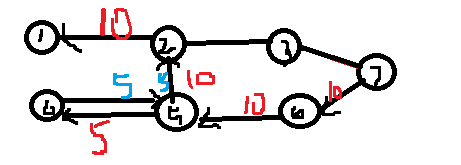
The red number represents the amount of backflow. I will not mark the side of 2 - > 3 for the time being. If f < C in the residual network, I will connect it with a back side. Don't ask me why, take your time. The size of the side connected back is to increase the traffic on the road. The original side is c-f, and the side with 0 traffic does not appear in the residual network.
Now let's talk about what the opposite side is used for. You see, if we add an opposite side to 2 - > 5, can 4 reach the confluence point 7 through the opposite side? The original graph can't because the side of 5, 6 is full. So, if we don't add the opposite side, there will be a road that can't be found. That's very embarrassing, ^ __________
In other words, adding an opposite side is to give the program a chance to repent. In reality, the opposite side does not exist, but appears in the program. In fact, this is equivalent to 4 - > 5 traffic to 2 - > 3, the first way to 1, 2, 3, 7, the second way to 4, 5, 6, 7. So, is it better to understand?
Next, let me talk about the EK code.

//Don't care too much about code style.
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm> 
#include<iostream>
#include<cstdio>
#define For(a,b,c) for(a=b;a<=c;a++)
#include<queue>
#define inf 999999999
using namespace std;
const int maxn = 1010;
int rong[510][510],liu[510][510];
int p[maxn];
int m,n;
int pre[maxn];
int sum;
void internet(){
    queue<int> q;
    while(1){//bfs is used to find the optical path, and ans + = the flow on the optical path.
        int i,j;
        memset(p,0,sizeof(p));
        p[1]=inf;//The p array here has two functions: one is to mark the non-accessed and the other is to remember the bottlenecks on the augmented path.
        q.push(1);
        while(!q.empty()){
            int ans=q.front();
            q.pop();
            For(i,1,n){
                if(!p[i]&&liu[ans][i]<rong[ans][i]){
                    p[i]=min(p[ans],rong[ans][i]-liu[ans][i]);
                    pre[i]=ans;//Record Enlargement Road.
                    q.push(i);
                }
            }
        }
        if(!p[n]){
            break;//If the augmentation path can not be found at point n, it means that the augmentation road has not reached the confluence point.
        }
        sum+=p[n];
        int tmp=n;
        while(pre[tmp]){//Continuously adjust the flow size.
            liu[pre[tmp]][tmp]+=p[n];
            liu[tmp][pre[tmp]]-=p[n];
            tmp=pre[tmp];
        }
    }
}
int main(){
    int i,j,k;
    int x,y,z;

    while(scanf("%d%d",&m,&n)!=EOF){
        sum=0;
        memset(pre,0,sizeof(pre));
        memset(rong,0,sizeof(rong));
        memset(liu,0,sizeof(liu));
        For(i,1,m){
            scanf("%d%d%d",&x,&y,&z);
            rong[x][y]+=z;
        }
        internet();
        printf("%d\n",sum);
    }
    return 0;
}

Well, EK, it's still very simple. Let's talk about dinic.
What is dinik? It is a faster algorithm than EK. It is similar to hk algorithm in bipartite graph matching. dinic uses a depth label, which is obtained by bfs. According to the nature of bfs, the size of the label increases strictly according to distance. The same label is used in the same layer of the search tree. As shown in the figure, the blue number is the depth label:

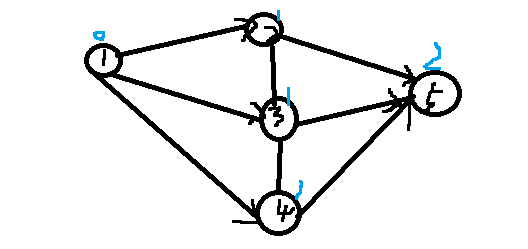
It's very impressive, if bfs can't, it's better not to touch the network flow first, then we use dfs to search according to the depth label strictly increasing or decreasing (see from the source or sink point), and then it's better. So why? Because as I said before, in fact, in the path from 1 to 5, we can only observe with the naked eye that the middle edges of 1, 2, 5, and 1, 3, 5 do not flow, because the reverse edges added from time to time do not exist, if we can search for elements strictly by increasing or decreasing according to the label, then relax.

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>

using namespace std;

#define REP(i,a,b) for(register int i = (a), i##_end_ = (b); i <= i##_end_; ++i)

inline int read()
{
    register int c = getchar(), fg = 1, sum = 0;
    while(c > '9' || c < '0' ) { if(c == '-')fg = -1; c = getchar();}
    while(c <= '9' && c >= '0') {sum = sum *10 + c - '0';c = getchar();}
    return fg * sum;
}
const int maxn = 1010;
int n,m;
int be[maxn], ne[maxn], to[maxn], e = 0, w[maxn]; 
int d[maxn];

void add(int x,int y,int z)
{
    to[e] = y;
    ne[e] = be[x];
    be[x] = e;
    w[e] = z;
    e++;
}


int bfs()
{
    memset(d,-1,sizeof(d));
    queue<int>q;
    q.push(n),d[n] = 0;
    while(!q.empty())
    {
        int u = q.front();
        q.pop();//Why is it i here? What about =-1? Because the label starts at zero.
        for(int i = be[u]; i!=-1; i = ne[i])
        {
            int v = to[i];//Here ^ is very common, because the forward star plus side is two together, but the reverse side is zero at first, so ^ 1 can get another side at once, such as 0 ^ 1 = 1, 1 ^ 1 = 0, 2 ^ 1 = 3, 3 ^ 1 = 2;
            if(w[i ^ 1] && d[v] == -1)
            {
                d[v] = d[u] + 1;
                q.push(v);
            }
        }
    }
    return d[1] != -1 ;
}

int dfs(int x,int low)
{
    if(x == n)return low;//low is the bottleneck.
    int k;
    for(int i = be[x]; i!=-1 ; i = ne[i])
    {
        int v = to[i];
        if(w[i] && d[v] == d[x] - 1 )
        {
            k = dfs(v,min(low,w[i]));
            if(k>0){
                w[i] -= k;
                w[i^1] += k;
                return k;
            }
        }
    }
    return 0;
}

int main()
{
    while(scanf("%d%d",&m,&n)!=EOF)
    {    e = 0;
        memset(be,-1,sizeof(be));
        REP(i,1,m)
        {
            int x,y,z;
            x = read(), y = read(), z = read();
            add(x,y,z);
            add(y,x,0);
        }
        int ans = 0,k;
        while(bfs())
        {
            k = dfs(1,1e7);
            ans += k;
        }
        printf("%d\n",ans);
    }
}

III: Cost Flow

Here we only talk about the minimum cost flow. We just talk about the replacement of bfs in EK with spfa because there is a cost on every side of the network.

/*************************************************************************
    > File Name: poj2195_Going_Home.cpp
    > Author: Drinkwater-cnyali
    > Created Time: 2017/2/12 8:47:55
************************************************************************/

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>


using namespace std;

#define REP(i, a, b) for(register int i = (a), i##_end_ = (b); i <= i##_end_; ++ i)
#define DREP(i, a, b) for(register int i = (a), i##_end_ = (b); i >= i##_end_; -- i)
#define mem(a, b) memset((a), b, sizeof(a))
#define inf 999999999

int read()
{
    int sum = 0, fg = 1; char c = getchar();
    while(c < '0' || c > '9') { if (c == '-') fg = -1; c = getchar(); }
    while(c >= '0' && c <= '9') { sum = sum * 10 + c - '0'; c = getchar(); }
    return sum * fg;
}

int n,m,num1 = 0,num2 = 0;
int be[100010], ne[100010], to[100010], c[100010], w[100010], e;
char s[200];
int pre[20010],id[20010],p[20010],d[20010];

struct T
{
    int x,y;
}H[10010],hm[10010];

void add(int x,int y,int ci,int wi)
{
    to[e] = y; ne[e] = be[x]; be[x] = e;
    c[e] = ci; w[e] = wi; e++;
    to[e] = x; ne[e] = be[y]; be[y] = e;
    c[e] = 0; w[e] = -wi; e++;
}

bool spfa()
{
    queue<int>q;
    REP(i,0,num1+num2+1)d[i] = inf;
    memset(pre,-1,sizeof(pre));
    memset(id,-1,sizeof(id));
    memset(p,0,sizeof(p));
    q.push(0),d[0] = 0, p[0] = 1;
    while(!q.empty())
    {
        int u = q.front();
        q.pop();
        p[u] = 0;
        for(int i = be[u]; i != -1 ; i = ne[i])
        {
            int v = to[i];
            if(c[i])
            {
                if(d[v] > d[u] + w[i])
                {
                    d[v] = d[u] + w[i];
                    pre[v] = u;
                    id[v] = i;
                    if(!p[v])
                    {
                        q.push(v);
                        p[v] = 1;
                    }
                }
            }
        }
    }
    return d[num1+num2+1] < inf;
}

int calc()
{
    int sum = 0, flow = inf;
    for(int i = num1+num2+1; pre[i]!= -1; i = pre[i])flow = min(flow, c[id[i]]);
    for(int i = num1+num2+1; pre[i]!= -1; i = pre[i])
    {
        sum+=w[id[i]] * flow;
        c[id[i]] -= flow;
        c[id[i] ^ 1] += flow;
    }
    return sum;
}

int main()
{
    while(1)
    {
        n = read(), m = read();
        if(n == 0 && m == 0)break;
        memset(H,0,sizeof(H));
        memset(hm,0,sizeof(hm));
        memset(be,-1,sizeof(be));
        e = 0;
        num1 =  num2 =0;
        REP(i,1,n)
        {
            scanf("%s",s);  
            REP(j, 0, strlen(s) - 1)
            {
                if(s[j] == 'H')H[++num1].x = i, H[num1].y = j+1;
                if(s[j] == 'm')hm[++num2].x = i,hm[num2].y = j+1;
            }
        }
        REP(i, 1, num1)
            REP(j,1,num2){
                int k = abs(H[i].x-hm[j].x)+abs(H[i].y-hm[j].y);
                add(i,j+num1,1,k);
            }
        REP(i, 1, num1)add(0,i,1,0);
        int k = num1 + num2 + 1;
        REP(i,num1+1,num1+num2)add(i,k,1,0);
        int ans = 0;
        while(spfa())ans += calc();
        printf("%d\n",ans);
    }
    return 0;
}
//A template for reference.