subject

A two-dimensional grid map grid of row x col is given, where grid[i][j] = 1 represents land and grid[i][j] = 0 represents water.
The grids in the grid are connected horizontally and vertically (not diagonally). The whole grid is completely surrounded by water, but there happens to be an island (or an island connected by one or more grids representing land).
There is no "Lake" in the island ("Lake" means that the water is inside the island and not connected to the water around the island). A lattice is a square with one side. The grid is rectangular, and the width and height do not exceed 100. Calculate the perimeter of the island.
Example 1

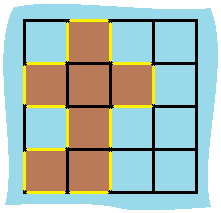
Input: grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
Output: 16
 Explanation: its circumference is the 16 yellow edges in the picture above

Example 2

Input: grid = [[1]]
Output: 4

Example 3

Input: grid = [[1,0]]
Output: 4

Tips

 1. row == grid.length
 2. col == grid[i].length
 3. 1 <= row, col <= 100
 4. grid[i][j] Is 0 or 1

thinking

Today's question is different from yesterday's Area surrounded by DFS release buckle 130 This question is very similar. First, let's read the question stem to find the key information
1.grid[i][j] = 1 indicates land, and grid[i][j] = 0 indicates water area
At this time, we know that this matrix represents a map with the size of row x col

2. Connect horizontally and vertically (not diagonally)
Specifies the direction in which water or land are connected

3. The whole grid is completely surrounded by water, but there happens to be an island
Note that there is only one island in this question

Therefore, the meaning of this question is to find the circumference of the shape composed of 1. Here, because we can't confirm the position of this land, we need to traverse once for dfs, and after entering dfs, if the current point is equal to 1 (that is, land), change its value to another one, such as 2, Then continue the search in the up, down, left and right directions. Let's look at the code directly

code

First, let's look at the main function. We use a double loop to traverse every point of the matrix
For each point, if the point value of the entry is 1, we add the value of this point, otherwise we do not add it

class Solution {
	int m, n;
	int islandPerimeter(vector<vector<int>>& grid) {
        m = int(grid.size());
        n = int(grid[0].size());
        int ans = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 1) {
                    ans += dfs(grid, i, j);
                }
            }
        }
        return ans;
    }
}；

The exit condition of dfs should be that the coordinates do not conform to the rules or the current search point value is 0 (which means that the land boundary is searched)

int dfs(vector<vector<int>>& grid, int x, int y) {
	if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
	            return 1;
	}
}

The reason for returning 1 is that this side of the land should also be included in the perimeter when searching the water area, so return 1
Then we need to judge whether the current point has been accessed. If so, we directly return 0

int dfs(vector<vector<int>>& grid, int x, int y) {
		if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
		            return 1;
		}
		if(grid[x][y] == 2) {
			return 0;
		}	
}

After all judgment conditions are completed, we need to mark the currently accessed point and change the value to 2 to facilitate our subsequent search judgment
Then finally, search the top, bottom, left and right of the current point

int dfs(vector<vector<int>>& grid, int x, int y) {
        if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
            return 1;
        }
        if(grid[x][y] == 2) {
            return 0;
        }
        grid[x][y] = 2;
        return dfs(grid, x + 1, y) + dfs(grid, x - 1, y) + dfs(grid, x, y + 1) + dfs(grid, x, y - 1);
}

Then we summarize the code together
Full code:

class Solution {
public:
    int m, n;
    int dfs(vector<vector<int>>& grid, int x, int y) {
        if(x < 0 || x >= m || y < 0 || y >= n || grid[x][y] == 0) {
            return 1;
        }
        if(grid[x][y] == 2) {
            return 0;
        }
        grid[x][y] = 2;
        return dfs(grid, x + 1, y) + dfs(grid, x - 1, y) + dfs(grid, x, y + 1) + dfs(grid, x, y - 1);
    }
    int islandPerimeter(vector<vector<int>>& grid) {
        m = int(grid.size());
        n = int(grid[0].size());
        int ans = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 1) {
                    ans += dfs(grid, i, j);
                }
            }
        }
        return ans;
    }
};