Purpose:
It is mainly used in key value search
- map
- nginx Timer event management
- Epoll event block management
- cfs
- memory management
Like malloc
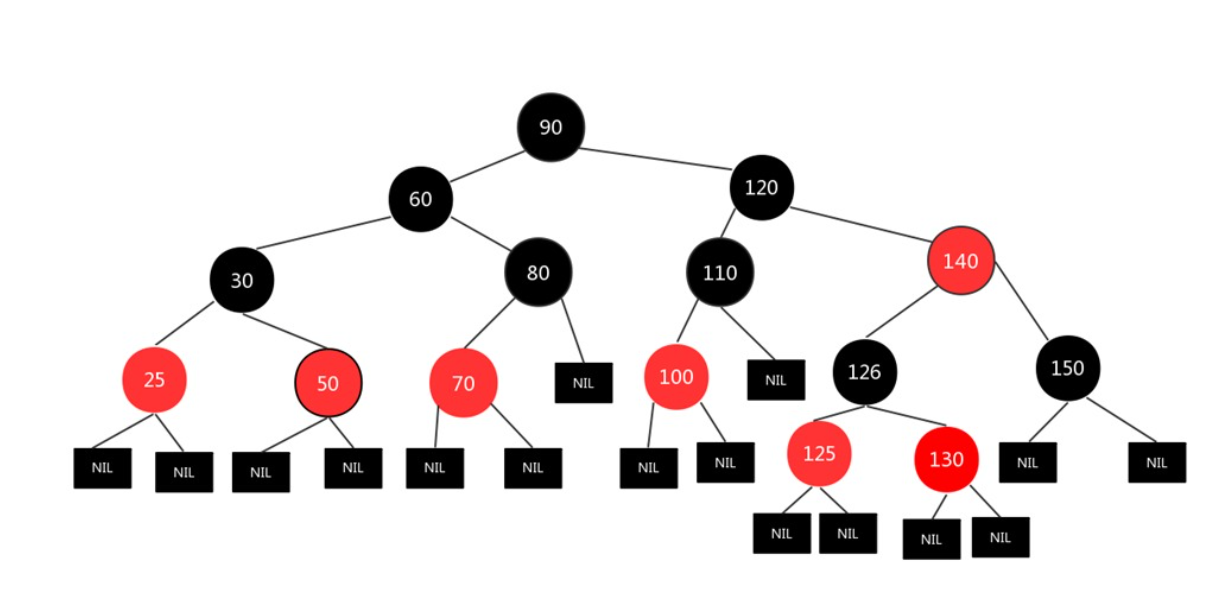
Sketch Map
Red black tree characteristics:
1, Each node is red or black
2, The root node is black
3, Each leaf node is black and hidden
4, If a node is red, its child nodes are black
5, For a node, all paths from the node to its descendants contain the same number of black nodes (balanced black height of red black tree)
6, The maximum path will not exceed twice the shortest path (because red must be followed by black, and the number of black nodes must be equal).
realization
Red black tree time complexity: O(lgn)
Red black tree application:
It is mainly used to store data, such as TreeSet and TreeMap in Java collection, set and map in C + +, and virtual memory management in linux
Red black tree - left-handed
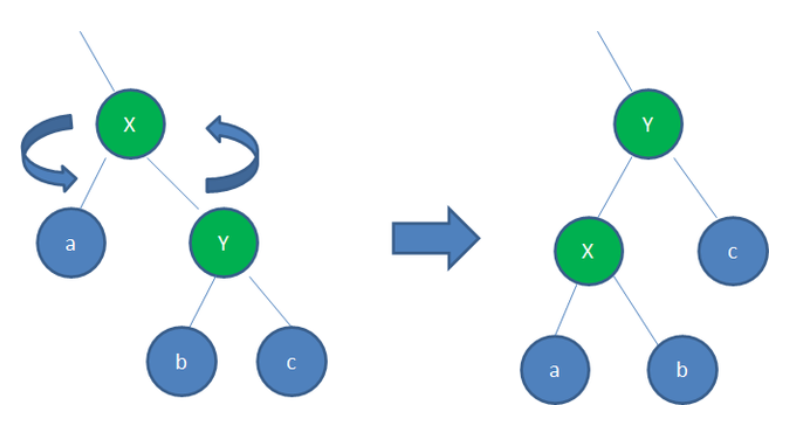
So it is said in the introduction to algorithm
LEFT-ROTATE(T, x) y ← right[x] // Premise: let's assume that the right child of x is y. Let's start the formal operation right[x] ← left[y] // Set "y's left child" to "x's right child", about to β Right child set to x p[left[y]] ← x // Set "x" to "y's left child's father", about to β The father of is set to x p[y] ← p[x] // Set "father of x" to "father of y" if p[x] = nil[T] then root[T] ← y // Case 1: if "x's father" is an empty node, set y as the root node else if x = left[p[x]] then left[p[x]] ← y // Case 2: if x is the left child of its parent node, set y as "the left child of X's parent node" else right[p[x]] ← y // Case 3: (x is the right child of its parent node) set y as "the right child of X's parent node" left[y] ← x // Set "x" to "y's left child" p[x] ← y // Set "parent of x" to "y"
void _left_route(rbtree *T, rbtree_node * x)
{
rbtree_node *y = x->right;
x->right = y->left;
if(y->left != T->nil)
y->left->parent = x;
if(x->parent != T->nil)
{
y->parent = T->root;
}
else if(x == x->parent->left)
{
x->parent->left = y;
}
else if(x == x->parent->right)
{
x->parent->right = y;
}
y->parent = x->parent;
x->parent = y;
y->left = x;
}
Red black tree - right rotation
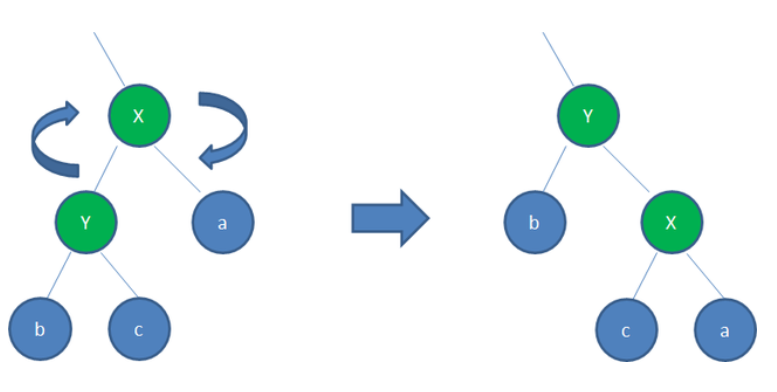
It is said in the introduction to algorithm:
RIGHT-ROTATE(T, y) x ← left[y] // Premise: let's assume that the left child of y is x. Let's start the formal operation left[y] ← right[x] // Set "x's right child" to "Y's left child", about to β Left child set to y p[right[x]] ← y // Set "Y" to "the father of the right child of x", about to β My father is set to y p[x] ← p[y] // Set "father of y" to "father of x" if p[y] = nil[T] then root[T] ← x // Case 1: if "y's father" is an empty node, set x as the root node else if y = right[p[y]] then right[p[y]] ← x // Case 2: if y is the right child of its parent node, set x as "the left child of Y's parent node" else left[p[y]] ← x // Case 3: (y is the left child of its parent node) set x as "the left child of Y's parent node" right[x] ← y // Set "y" to "right child of x" p[y] ← x // Set "parent node of y" to "x"
void _right_route(rbtree *T, rbtree_node * x)
{
rbtree_node *y = x->left;
x->left= y->right;
if(y->right!= T->nil)
y->right->parent = x;
if(x->parent != T->nil)
{
y->parent = T->root;
}
else if(x == x->parent->left)
{
x->parent->left = y;
}
else if(x == x->parent->right)
{
x->parent->right = y;
}
y->parent = x->parent;
x->parent = y;
y->right= x;
}
The red black tree is a binary tree, and the binary tree must meet the sorting requirements. Therefore, the left and right rotation of the red black tree only changes the parent-child node relationship of X and Y nodes
Red black tree addition
Red black trees can be added in the following ways:
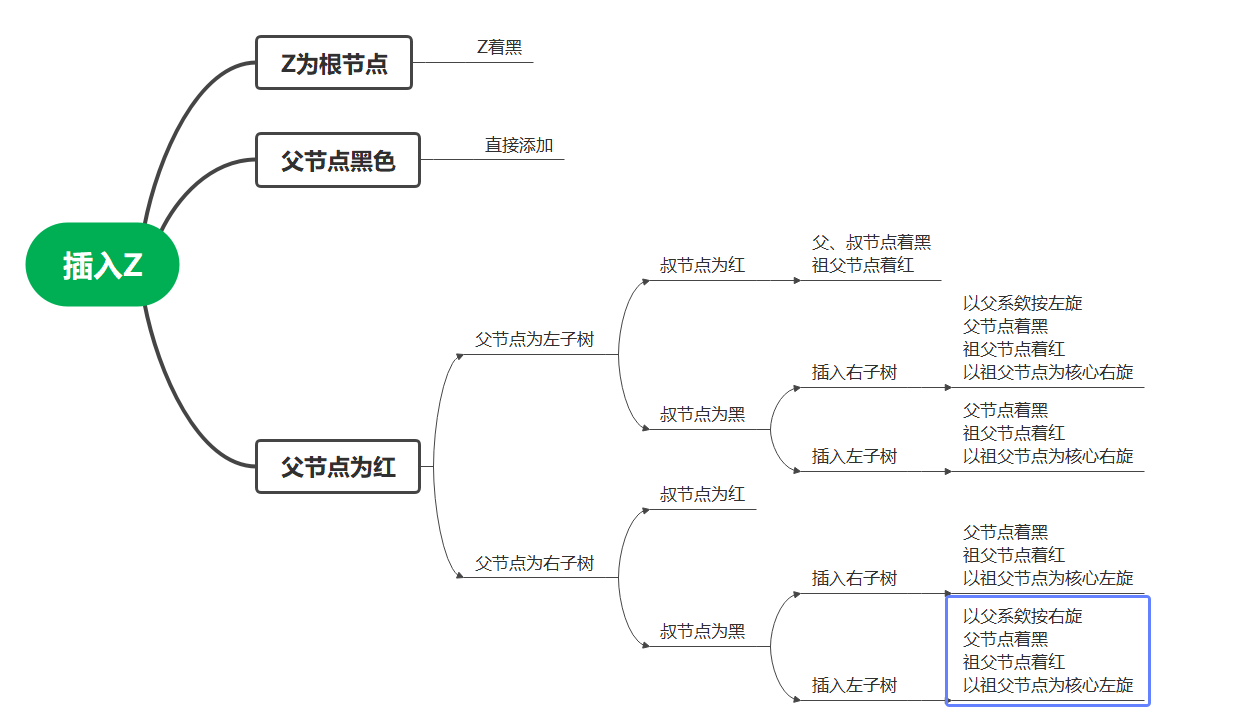
The red part of the parent node in the above figure can be summarized into three cases,
- The parent node is red and the uncle node is red
Processing method: transform the parent node and uncle node to black and the grandfather node to red. Then process the grandfather node to meet the red black tree value: the child node of the red node cannot be red! - The parent node is red and the uncle node is black. The parent node and the current node are on the same side of the tree, either the left subtree of the parent node or the right subtree of the parent node
Processing method: rotate the grandfather node so that the parent node is in the position of the previous grandfather node, exchange the colors of the parent node and the grandfather node, so that the original grandfather node is still in black and its two child nodes become red - The parent node is red, the uncle node is black, and the parent node is in a different state from the current node.
Processing method: transform two consecutive red to the same side as the parent node by rotation, and then process according to the second case.
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
while (z->parent->color == RED) { //z ---> RED
if (z->parent == z->parent->parent->left) {
rbtree_node *y = z->parent->parent->right;
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
//Make sure that the current node and the parent node are on the same side of the tree. If not, rotate and transform a red node to the same side, and then hand over the node handle.
//The core of the transformation here is to pull one of the two consecutive red nodes to the position of the grandfather node through rotation, and then color. In this way, the black height will not be changed to achieve balance
if (z == z->parent->right) {
z = z->parent;
_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
_right_rotate(T, z->parent->parent);
}
}else {
rbtree_node *y = z->parent->parent->left;
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->left) {
z = z->parent;
_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
//Find the location where the z node should be added, and refer to the binary tree property value
while (x != T->nil) {
y = x;
if (z->key < x->key) {
x = x->left;
} else if (z->key > x->key) {
x = x->right;
} else { //Exist
return ;
}
}
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
//Red
z->color = RED;
//Modify the color to meet the red black tree property value
rbtree_insert_fixup(T, z);
}
Delete node
Three node definitions
- Overwrite node z: the node corresponding to the key you want to delete
- Delete node y: the minimum value of the actually released node at the right node of z. if z is missing the left and right subtrees, it overlaps with x
- The child node of the pivot node x: y, from which the red and black attributes are adjusted
To delete a node
- Find x, y nodes
- Disconnect the Y node and graft the x node to the original y node.
- Copy the contents of the y node to the z node
- If the deleted node y is a black node, adjust the red and black so that the tree still meets the red and black tree attribute
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->nil;
// Find x, y nodes
if ((z->left == T->nil) || (z->right == T->nil)) {
y = z;
} else {
y = z->right;
while(y->left != T->nil)
{
y = y->left;
}
}
if (y->left != T->nil) {
x = y->left;
} else if (y->right != T->nil) {
x = y->right;
}
// Delete y node
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->left) {
y->parent->left = x;
} else {
y->parent->right = x;
}
if (y != z) {
z->key = y->key;
z->value = y->value;
}
if (y->color == BLACK) {
rbtree_delete_fixup(T, x);
}
free(y);
}
Adjust red black tree attributes
There may be a situation when adjusting the tree. x is red. Since neither parent nor child nodes in red can be red, it is good to dye black directly, which is not discussed here.
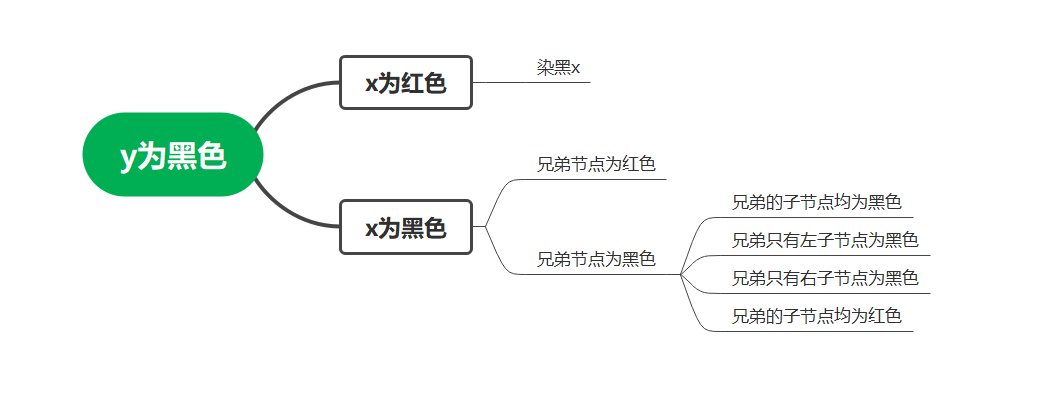
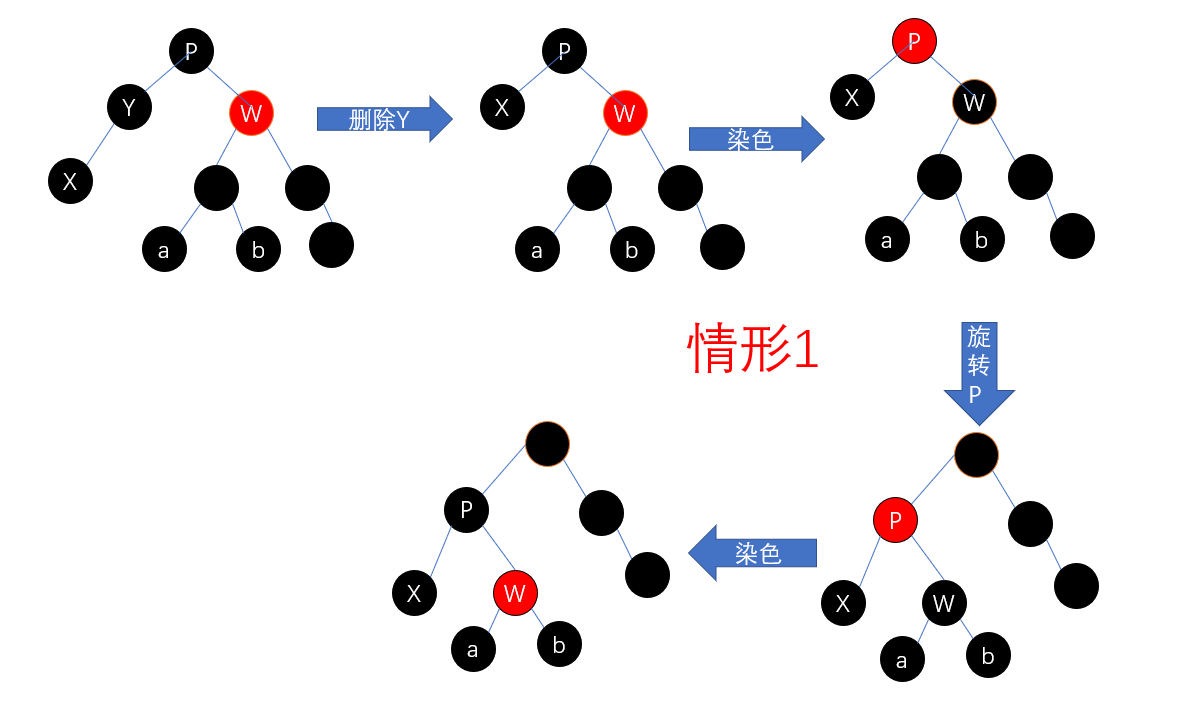
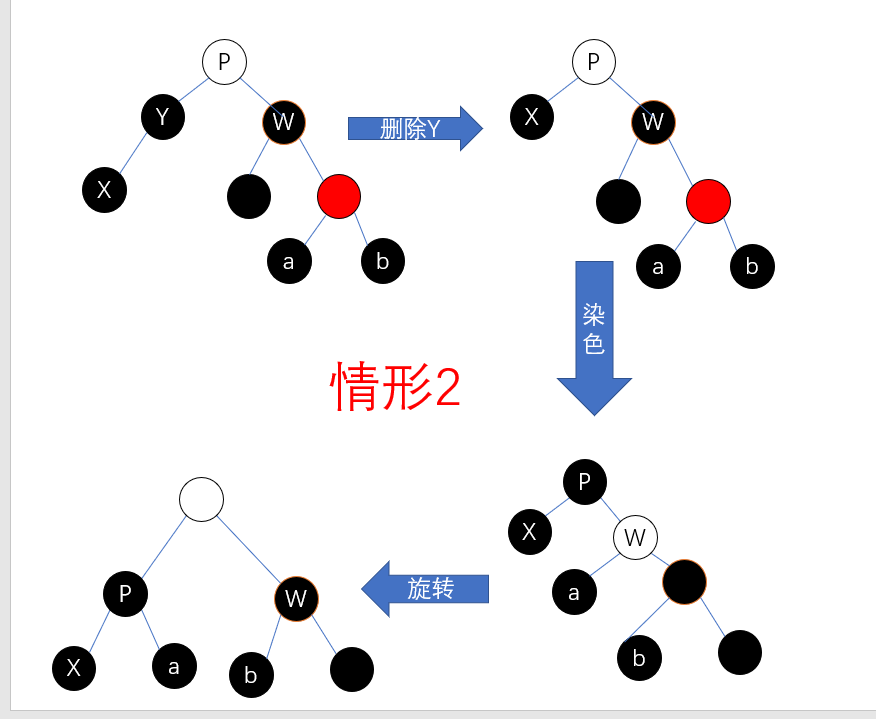
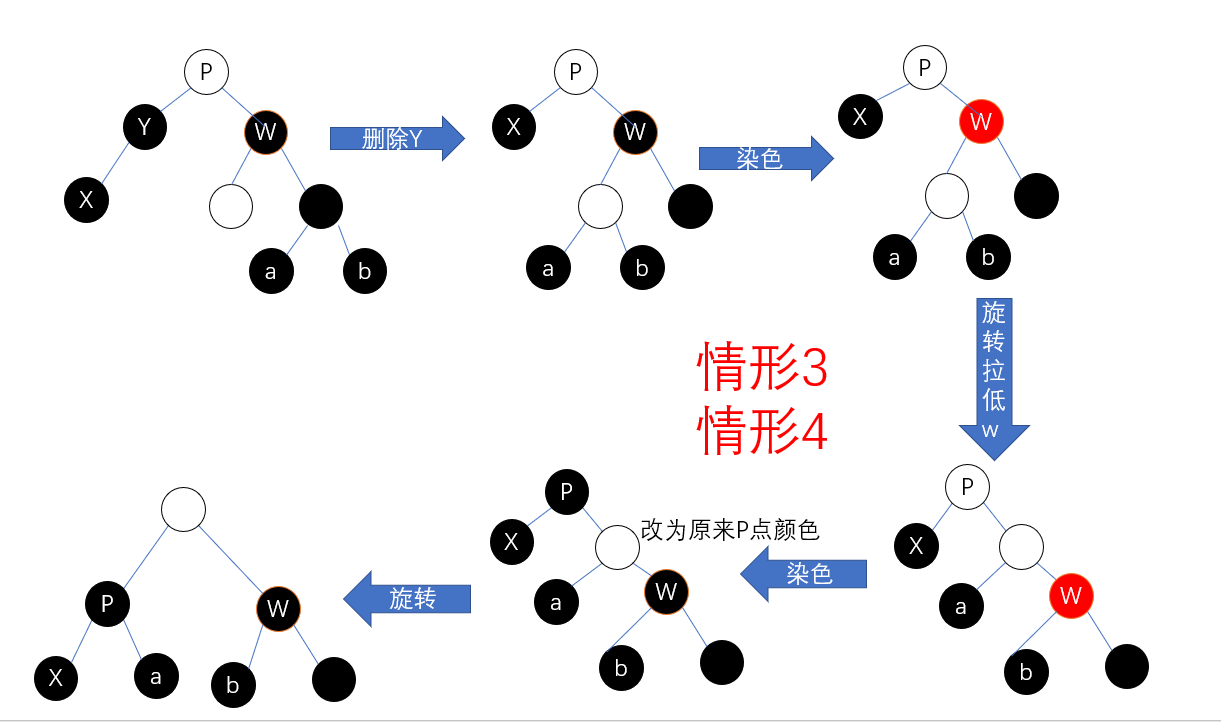
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {
while ((x != T->root) && (x->color == BLACK)) {
if (x == x->parent->left) {
rbtree_node *w= x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
_left_rotate(T, x->parent);
w = x->parent->right;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
_right_rotate(T, w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
_left_rotate(T, x->parent);
x = T->root;
}
} else {
rbtree_node *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
_right_rotate(T, x->parent);
w = x->parent->left;
}
if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
_left_rotate(T, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
_right_rotate(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}