Deep learning_ Perceptron

Reference books: introduction to deep learning_ Theory and Implementation Based on python

1. Perceptron
1.1 principle: receive multiple input signals and output one signal
1.2 diagram:

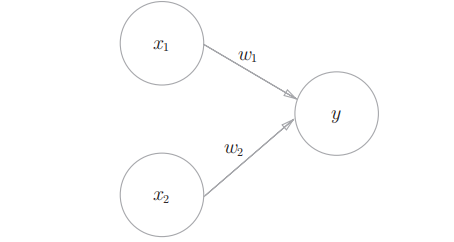
1.3 diagram: the above figure shows a perceptron receiving two input signals, X1 and X2 are input signals, y are output signals, w1 and w2 are weights, and O in the figure is called "neuron" or "node". When input signals are sent to neurons, they are multiplied by fixed weights (w1x1, w2x2) respectively. The neuron calculates the sum of the transmitted signals and outputs 1 only when the sum exceeds a certain limit value. This is also known as "neurons are activated". This limit value is called the threshold value and is represented by a symbol θ express.
1.4 formula:

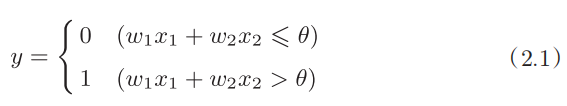
1.5 weight: the greater the weight of the perceptron, the greater the passing signal
2. Simple logic circuit
2.1 and doors
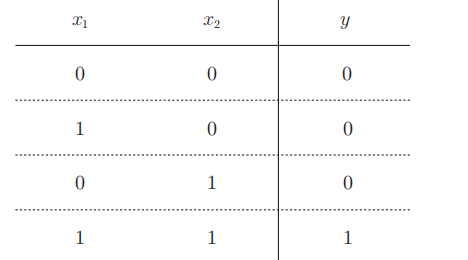
2.1.1 principle: gate circuit with two inputs and one output
2.1.2 truth table:

2.2 NAND gate
2.2.1 principle: the output of and gate is reversed
2.2.2 truth table:

2.3 or door
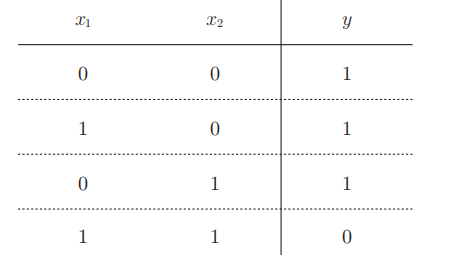
2.3.1 principle: as long as one input signal is 1, the output is 1
2.3.2 truth table:

3. Implementation of perceptron
3.1 simple implementation
3.1.1 and door

def And(x1,x2):
    w1,w2,theta=0.7,0.3,0.7
    tmp=x1*w1+x2*w2
    if tmp<=theta:
        return 0
    elif tmp>theta:
        return 1

a=And(0,0)
print(a)   #0

b=And(0,1)
print(b)    #0

c=And(1,0)
print(c)     #0

d=And(1,1)
print(d)   #1

3.1.2 NAND gate

#NAND gate
def And(x1,x2):
    w1,w2,theta=-0.5,-0.5,-0.7
    tmp=x1*w1+x2*w2
    if tmp<=theta:
        return 0
    elif tmp>theta:
        return 1

a=And(0,0)
print(a)   #1

b=And(0,1)
print(b)    #1

c=And(1,0)
print(c)     #1

d=And(1,1)
print(d)   #0

3.1.3 or door

#Or gate
def And(x1,x2):
    w1,w2,theta=1,1,0
    tmp=x1*w1+x2*w2
    if tmp<=theta:
        return 0
    elif tmp>theta:
        return 1

a=And(0,0)
print(a)   #0

b=And(0,1)
print(b)    #1

c=And(1,0)
print(c)     #1

d=And(1,1)
print(d)   #1

3.2 import weights and offsets
3.2.1 principle:

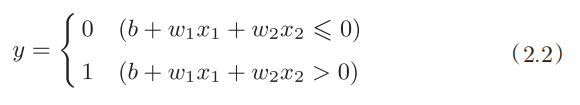
3.2.2 interpretation of formula: integrate the formula of formula (2.1) θ Change to − b, b is called bias, the value of bias determines the ease of activation of neurons, and w1 and w2 are called weights. The perception opportunity calculates the product of the input signal and the weight, and then adds the offset. If the value is greater than 0, it outputs 1, otherwise it outputs 0
3.3 implementation using weights and offsets
3.3.1 and door:

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = AND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

# (0, 0) -> 0
# (1, 0) -> 0
# (0, 1) -> 0
# (1, 1) -> 1

3.3.2 non gate

import numpy as np

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

# (0, 0) -> 1
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 0

3.3.3 or door

import numpy as np

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

# (0, 0) -> 0
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 1

4. Limitations of perceptron
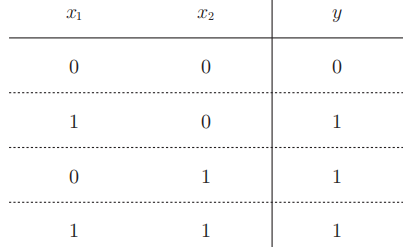
4.1 XOR gate:
4.1.1 principle: only when one of x1 or x2 is 1, 1 will be output; Perceptron cannot be realized by XOR gate
4.1.2 truth table of XOR gate:

4.2 linearity and nonlinearity
4.2.1 linear space: space divided by curve
4.2.2 nonlinear space: space divided by straight lines
5. Multi layer perceptron
5.1 existing gate circuit combination
5.1.1 and gate, NAND gate, or gate:

5.1.2 realize XOR gate with and gate, NAND gate, or gate:

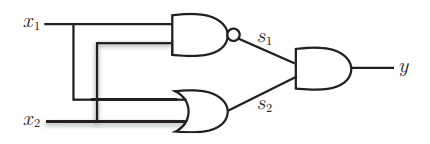
5.1.2 realization of XOR gate

from and_gate import AND
from or_gate import OR
from nand_gate import NAND

def XOR(x1, x2):
    s1 = NAND(x1, x2)  #NAND gate
    s2 = OR(x1, x2)   #Or gate
    y = AND(s1, s2)   #And gate
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

# (0, 0) -> 0
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 0

5.1.3 layer 2 perceptron
Principle:
1. Two neurons in layer 0 receive input signals and send signals to neurons in layer 1.
2. Layer 1 neurons send signals to layer 2 neurons, and layer 2 neurons output y.