html http://cmsblogs.com/ 『chenssy』
We know that thread Thread can call setPriority (int new Priority) to set priority. Threads with high priority are executed first, and threads with low priority are executed later. The Array BlockingQueue and LinkedBlockingQueue introduced earlier all adopt FIFO principle to determine the sequence of thread execution. Is there a queue that can support priority? Priority Blocking Queue.
Priority Blocking Queue is an unbounded blocking queue that supports priority. By default, elements are sorted in natural ascending order. Of course, we can also specify Comparator by constructor to sort elements. It should be noted that Priority Blocking Queue does not guarantee the order of the same priority elements.
Two fork pile
Because the bottom of Priority Blocking Queue is implemented by binary heap, it is necessary to introduce the binary heap first.
Binary heap is a special kind of heap. In terms of structure, it is a complete binary tree or an approximate complete binary tree, which satisfies the tree structure and heap order. The tree mechanism is the structure that a complete binary tree should have. The heap ordering is that the key value of the parent node always keeps a fixed order relationship with the key value of any child node, and the left subtree and the right subtree of each node are a binary heap. It has two forms: maximum heap and minimum heap.
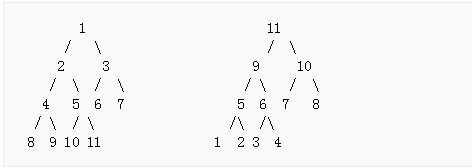
Maximum heap: The key value of the parent node is always greater than or equal to the key value of any child node (bottom right)
Minimum heap: The key value of the parent node is always less than or equal to the key value of any child node (next figure)
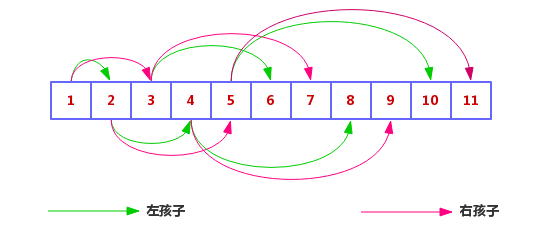
The binary heap is usually represented by an array. If the node of the parent node is located at n, then its left child node is 2 * n + 1, its right child node is 2 * (n + 1), and its parent node is (n - 1) / 2. The array representation of the upper left graph is as follows:
The basic structure of the binary heap is understood. Let's take a look at adding and deleting nodes in the binary heap. Adding and deleting binary heaps is much simpler than binary trees.
Additive elements
First, the element N to be added is inserted at the end of the heap (in binary heap, we call it holes). If element N is placed in a hole without destroying the heap order (its value is greater than that of the parent node (the maximum heap is smaller than that of the parent node), then insertion is complete. Otherwise, we swap the node of element N with its parent, and then compare it with its new parent until its parent is not smaller (the maximum heap is large) or reaches the root node.
If there is a binary heap like this
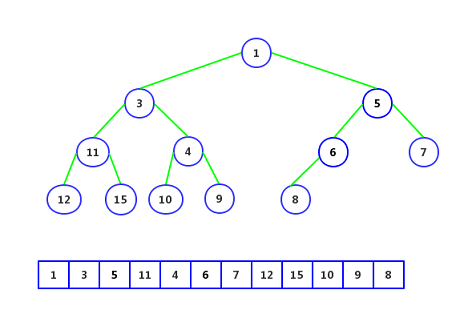
This is a minimal heap whose parent is always less than or equal to any child. Now let's add an element 2.
Step 1: Add an element 2 at the end, as follows:
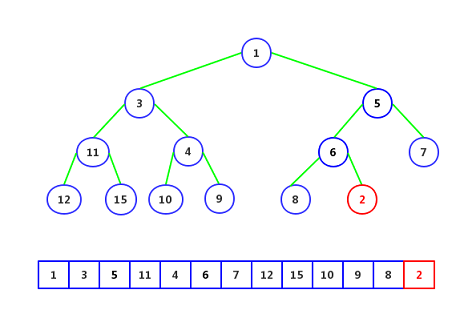
Step 2: Element 2 is smaller than its parent node 6 and is replaced as follows: 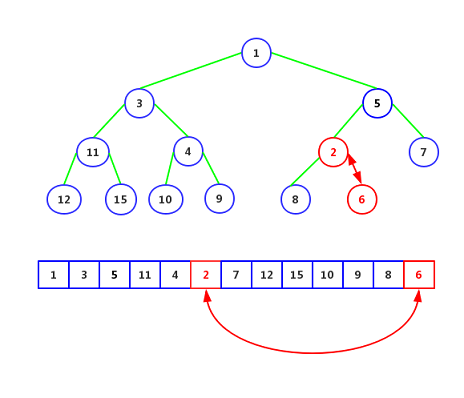
Step 3: Continue to compare with its parent node 5, less than, replace:
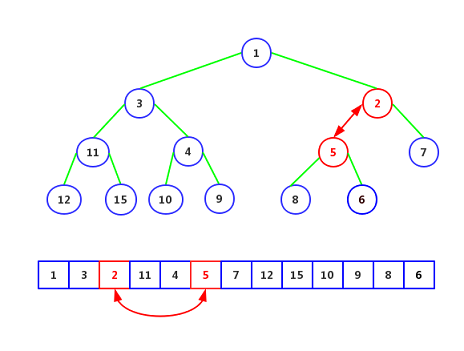
Step 4: Continue to compare its heel node 1 and find that the heel node is smaller than itself, then complete, and insert element 2 here. So the whole process of adding elements can be summarized as inserting elements at the end of elements, and then comparing and replacing them until they can not be moved.
Complexity: logn
Delete elements
Deleting elements, like adding elements, requires maintaining the order of the entire binary heap. Delete the element at position 1 (array subscript 0), move the last element out to the front, and then compare it with its two sub-nodes. If the smaller nodes in the two sub-nodes are smaller than the node, they are swapped, knowing that both sub-nodes are larger than the element.
For the binary heap above, the deleted element is element 1.
Step 1: Delete element 1 and empty element 6, as follows: 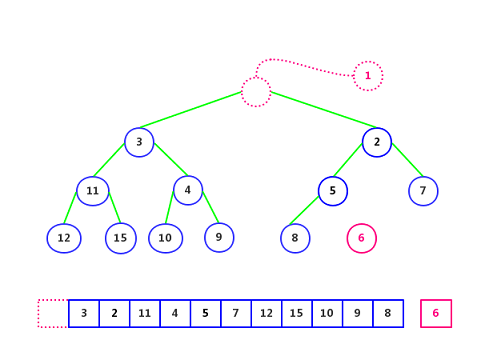
The second step: Comparing with its two sub-nodes (element 2 and element 3), they are smaller, and the smaller element (element 2) is put into the hole: 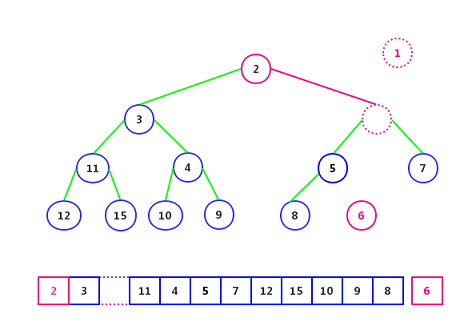
Step 3: Continue to compare the two sub-nodes (element 5, element 7) or are all small, then put the smaller elements (element 5) into the hole:! 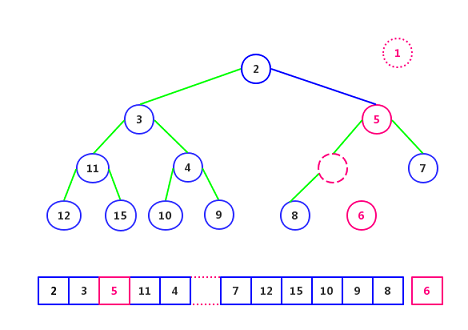
Step 4: Comparing its sub-nodes (Element 8), which are smaller than the node, the placement of Element 6 in the empty point will not affect the tree structure of the binary heap, and the placement of Element 6 in the empty point will not affect the tree structure of the binary heap.
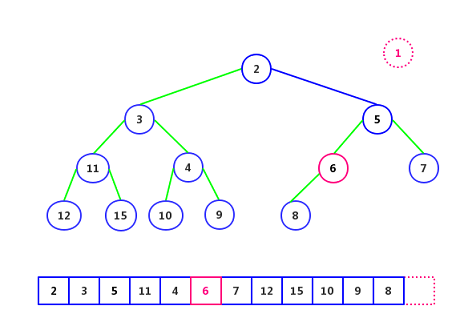
The entire deletion operation has been completed here.
The operation of adding and deleting binary heap is relatively simple and easy to understand. Next we will refer to this content to open Priority Blocking Queue source code research.
PriorityBlockingQueue
Priority BlockingQueue inherits AbstractQueue and implements the BlockingQueue interface.
public class PriorityBlockingQueue<E> extends AbstractQueue<E>
implements BlockingQueue<E>, java.io.Serializable Some properties are defined:
// Default capacity
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// Maximum capacity
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
// Binary heap array
private transient Object[] queue;
// Number of queue elements
private transient int size;
// Comparator, if empty, is in natural order
private transient Comparator<? super E> comparator;
// Internal lock
private final ReentrantLock lock;
private final Condition notEmpty;
//
private transient volatile int allocationSpinLock;
// Priority Queue: Mainly for serialization, this is for compatibility with previous versions. Only serialization and deserialization are not empty
private PriorityQueue<E> q;ReentrantLock is still used internally to achieve synchronization, but there's only one notEmpty Condition. Knowing Array Blocking Queue, we know that it defines two conditions. Why is there only one? The reason is that Priority Blocking Queue is an unbounded queue, and insertion always succeeds unless resources are exhausted and the server hangs.
List
PriorityBlockingQueue provides put(), add(), offer() methods to add elements to the queue. Let's start with put(): put (E): insert the specified element into this priority queue.
public void put(E e) {
offer(e); // never need to block
}Priority Blocking Queue is unbounded, so it's impossible to block. Internal Call offer (E):
public boolean offer(E e) {
// Can't be null
if (e == null)
throw new NullPointerException();
// Get lock
final ReentrantLock lock = this.lock;
lock.lock();
int n, cap;
Object[] array;
// Capacity expansion
while ((n = size) >= (cap = (array = queue).length))
tryGrow(array, cap);
try {
Comparator<? super E> cmp = comparator;
// Do different processing according to whether the comparator is null or not
if (cmp == null)
siftUpComparable(n, e, array);
else
siftUpUsingComparator(n, e, array, cmp);
size = n + 1;
// Wake up waiting consumer threads
notEmpty.signal();
} finally {
lock.unlock();
}
return true;
}siftUpComparable
When the comparator is null, the siftUpComparable method is invoked by natural sorting.
private static <T> void siftUpComparable(int k, T x, Object[] array) {
Comparable<? super T> key = (Comparable<? super T>) x;
// The process of "risking"
while (k > 0) {
// Parent node (n-)/ 2
int parent = (k - 1) >>> 1;
Object e = array[parent];
// Key >= parent completion (maximum heap)
if (key.compareTo((T) e) >= 0)
break;
// Key < parant replacement
array[k] = e;
k = parent;
}
array[k] = key;
}What this code means: insert element X into an array, and then adjust it to maintain the binary heap's properties.
siftUpUsingComparator
When the comparator is not null, the siftUpUsingComparator method is called using the specified comparator:
private static <T> void siftUpUsingComparator(int k, T x, Object[] array,
Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = array[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
array[k] = e;
k = parent;
}
array[k] = x;
}Expansion: tryGrow
private void tryGrow(Object[] array, int oldCap) {
lock.unlock(); // Expansion operation using spin, no need to lock the main lock, release
Object[] newArray = null;
// CAS occupancy
if (allocationSpinLock == 0 && UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset, 0, 1)) {
try {
// Minimum doubling of new capacity
int newCap = oldCap + ((oldCap < 64) ? (oldCap + 2) : (oldCap >> 1));
// Exceed
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
int minCap = oldCap + 1;
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
newCap = MAX_ARRAY_SIZE; // Maximum capacity
}
if (newCap > oldCap && queue == array)
newArray = new Object[newCap];
} finally {
allocationSpinLock = 0; // Allocation SpinLock = 0 after expansion represents the release of spin locks
}
}
// If this thread expands the capacity of newArray, it must not be null. For null, other threads are dealing with the expansion. Let other threads deal with it.
if (newArray == null)
Thread.yield();
// Main Lock Acquisition Lock
lock.lock();
// Array replication
if (newArray != null && queue == array) {
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}The whole process of adding elements is exactly the same as the binary heap above: first add elements to the end of the array, and then use the "riser" way to make the elements as risky as possible.
List out
PriorityBlockingQueue provides poll(), remove() methods to perform pair operations. The first element is always the right one: array[0].
public E poll() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return dequeue();
} finally {
lock.unlock();
}
}Get the lock first, and then call the dequeue() method:
private E dequeue() {
// No element returns null
int n = size - 1;
if (n < 0)
return null;
else {
Object[] array = queue;
// Out pair elements
E result = (E) array[0];
// The last element (that is, the element inserted into the hole)
E x = (E) array[n];
array[n] = null;
// Different processing is performed according to the release of the comparator to null
Comparator<? super E> cmp = comparator;
if (cmp == null)
siftDownComparable(0, x, array, n);
else
siftDownUsingComparator(0, x, array, n, cmp);
size = n;
return result;
}
}siftDownComparable
If the comparator is null, the siftDownComparable is called for natural sort processing:
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) {
Comparable<? super T> key = (Comparable<? super T>)x;
// The parent location of the last leaf node
int half = n >>> 1;
while (k < half) {
int child = (k << 1) + 1; // Left node position to be adjusted
Object c = array[child]; //Left node
int right = child + 1; //Right node
//Comparing left and right nodes, choose smaller ones.
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
c = array[child = right];
//If the key to be adjusted is the smallest, exit and assign it directly.
if (key.compareTo((T) c) <= 0)
break;
//If the key is not the smallest, then take the smaller one of the left and right nodes and place it in the adjustment position. Then the smaller one starts to adjust again.
array[k] = c;
k = child;
}
array[k] = key;
}
}The idea of processing is the same as the logic of deleting nodes in binary heap: the first element is defined as a hole, and then the last element is taken out and tried to insert into the empty point, and compared with the values of two sub-nodes. If not, it is replaced with the smaller sub-nodes, and then continues to compare and adjust.
siftDownUsingComparator
If a comparator is specified, the comparator is used to adjust:
private static <T> void siftDownUsingComparator(int k, T x, Object[] array,
int n,
Comparator<? super T> cmp) {
if (n > 0) {
int half = n >>> 1;
while (k < half) {
int child = (k << 1) + 1;
Object c = array[child];
int right = child + 1;
if (right < n && cmp.compare((T) c, (T) array[right]) > 0)
c = array[child = right];
if (cmp.compare(x, (T) c) <= 0)
break;
array[k] = c;
k = child;
}
array[k] = x;
}
}Priority BlockingQueue is maintained by binary heap, so the whole process is not very complicated. Adding operations are constantly "up" and deleting operations are "down". To master binary heap is to master Priority Blocking Queue, no matter how it changes or not. For Priority Blocking Queue, it's important to note that it's an unbounded queue, so adding operations won't fail unless resources are exhausted.
Welcome to sweep my public number attention - get blog subscriptions in time!
- The Way to Java Deity: 488391811 (Towards Java Deity Together) - 