Data type: divided into two categories
1. It is the type of c language itself, also known as built-in type
char Character type 1 byte short Short shaping 2 bytes int plastic four bytes long Long shaping 4/8 byte long long Longer shaping 8 bytes float Single-precision floating-point 4 bytes double Double precision floating point number 8 bytes
2. User defined type (construction type)
Meaning of type:
1. Use this type to open up the size of memory space (the size determines the scope of use) 2. How to view memory space
Plastic family
char unsigned char signed char short unsigned short (int) signed short (int) int unsigned int signed int long unsigned long (int) signed long (int)
Floating point family
float double
Construction type
Array type array Structure type struct Enumeration type enum Union type union
Pointer type
Shaping pointer int* pi; Character pointer char* pc; Floating point pointer float* pf; Typeless pointer (Universal pointer) void* pv; [Can only be received and cannot be used. If you want to use it, you need to force type conversion]
Empty type
1 .void Represents an empty type (no type) 2 .The return type, parameter and pointer type applied to the function
example
#include<stdio.h>
void test()// void here means that the function test has no return value
{
printf("hello!\n");
}
int main()
{
test();
return 0;
}
Shaping is stored in memory
Inverse complement of original code
There are three ways to express the integer (positive and negative) signed number in the computer: the original code, the inverse code, and the complement code (expressed in binary code) The three methods have two parts: sign bit and value bit. The sign bit (the highest bit of binary) is 0, which means positive and 1 means negative The three representation methods of numerical bits are different Original code: directly translate the shaping data into binary in the form of positive and negative. Inverse code: it can be obtained by changing the sign bit of the original code and inverting the other bits in turn Complement: inverse code+1 Note that the original inverse complement three codes of positive integers are the same
Instance (the highest bit of binary bit is the sign bit, 0 is positive and 1 is negative)
vs environment
#include<stdio.h>
int main()
{
int a = 20; // 00 14 integer data is represented and stored by complement
a Is a positive number, three yards are the same
//0000 0000 0001 0100 original code, a is a positive integer. So the three sizes are the same
//0000 0000 0001 0100 the sign bit of the original code remains unchanged, and other bits are reversed by bit
//0000 0001 0100 complement inverse plus one, the complement is stored in (a) memory
// 0 0 0 0 0 0 0 1 (16) 4 hex (every 16 into 1)
// After being stored in the memory, it is expressed as 14 00 00 (small end storage mode: the low byte content is stored in the low address, and the high byte content is stored in the high address)
int b = -10;// 0x FF F8 integer data is represented and stored by complement
// 1000 0000 1010 original code
// 1111 1111 1111 1111 1111 1111 1111 0101 the sign bit of the original code remains unchanged, and other bits are reversed by bit
// 1111 1111 1111 1111 1111 1111 1111 0110 complement inverse code plus one, and the complement is stored in (b) memory
// F 6 hex 0x ff ff F6
//After being stored in memory, it is expressed as F6 ff ff (small end storage mode: the low byte content is stored in the low address, and the high byte content is stored in the high address)
return 0;
}


In the computer system (internal storage), integers are always represented and stored by complement. The reason is that the symbol bit and value field can be processed uniformly by using complement. At the same time, addition and subtraction can also be processed uniformly (CPU only has adder). In addition, complement and original code are converted to each other. The operation process is the same, and no additional hardware computer is required.
example
#include<stdio.h>
int main()
{
1 - 1;
// The upper expression is 1 + (- 1) in the view of CPU, because CPU only has adder
What if we use the original code for calculation?
//00000000 00000000 00000000 00000001 / / 1 original code
//10000000 00000000 00000000 00000001 / / - 1 original code
//10000000 0000000 0000000 0000000 00000010 / / - 2 adding the original code, it is obvious that the operation with the original code is wrong, 1 - 1! =- 2 ,
//00000000 00000000 00000000 00000001 / / 1 Complement
//111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
//00000000 00000000 00000000 00000000 / / 0 two complements are added. It is obvious that the operation with complements is correct, 1 - 1 = = 0
return 0;
}
Integer (all shaping data are represented and stored by complement):
1. Signed number:
Positive number (the original inverse complement three codes are the same) Negative number (original code) -> The original code symbol bits remain unchanged, and the rest are reversed by bits -> Inverse code -> Plus 1 -> Complement[ )
2. Unsigned integer:
The original reverse complement three codes are the same
Concept of large and small end

Can it be stored in other ways? For example, 11 33 22 44, 44 22 33 11, etc
The answer is yes. As long as you can think of any storage method (but please note: how to put it in and how to take it out)
To facilitate data storage and reading
Therefore, positive deposit (small end) and reverse deposit (large end) are selected
In addition, hexadecimal numbers 11, 22, 33, 44 occupy one word section every two, which can also be said to be stored in byte order
Namely:
Large end (storage) mode means that the low bit of data is saved in the high address of memory, while the high bit of data is saved in the low address of memory
Also known as: large end byte order (storage) mode
Small end (storage) mode: it means that the low bit of data is saved in the low address of memory, while the high bit of data is saved in the high address of memory
Also known as: small end byte order (storage) mode
Meaning of large and small end mode:
Because in the computer system, we take bytes as the unit, and each address unit corresponds to a byte, a byte 8 bit. however C Language except 8 bit of char In addition, there are 16 bit of short,32 bit of long Type (depending on the specific compiler). For processors with more than 8 bits, such as 16 bit or 32-bit processors, since the register width is greater than one byte, there must be a problem of one or more bytes arrangement. Therefore, it is necessary to have large end storage mode and small end storage mode
example
#include<stdio.h>
int main()
{
int a = 20; // Memory condition: 14 00 (small end)
//0000 0000 0000 0000 0001 0100 original code, a is a positive integer, so the three codes are the same
//0000 0000 0001 0100 inverse code
//0000 0000 0000 0000 0001 0100 the complement is stored in a
// 0 0 0 0 0 1 (16) 4 hex 0x 00 14
return 0;
}
Case 1 (write a code to tell us what the byte order of the current machine is):
Writing method 1
vs environment
#include<stdio.h>
int main()
{
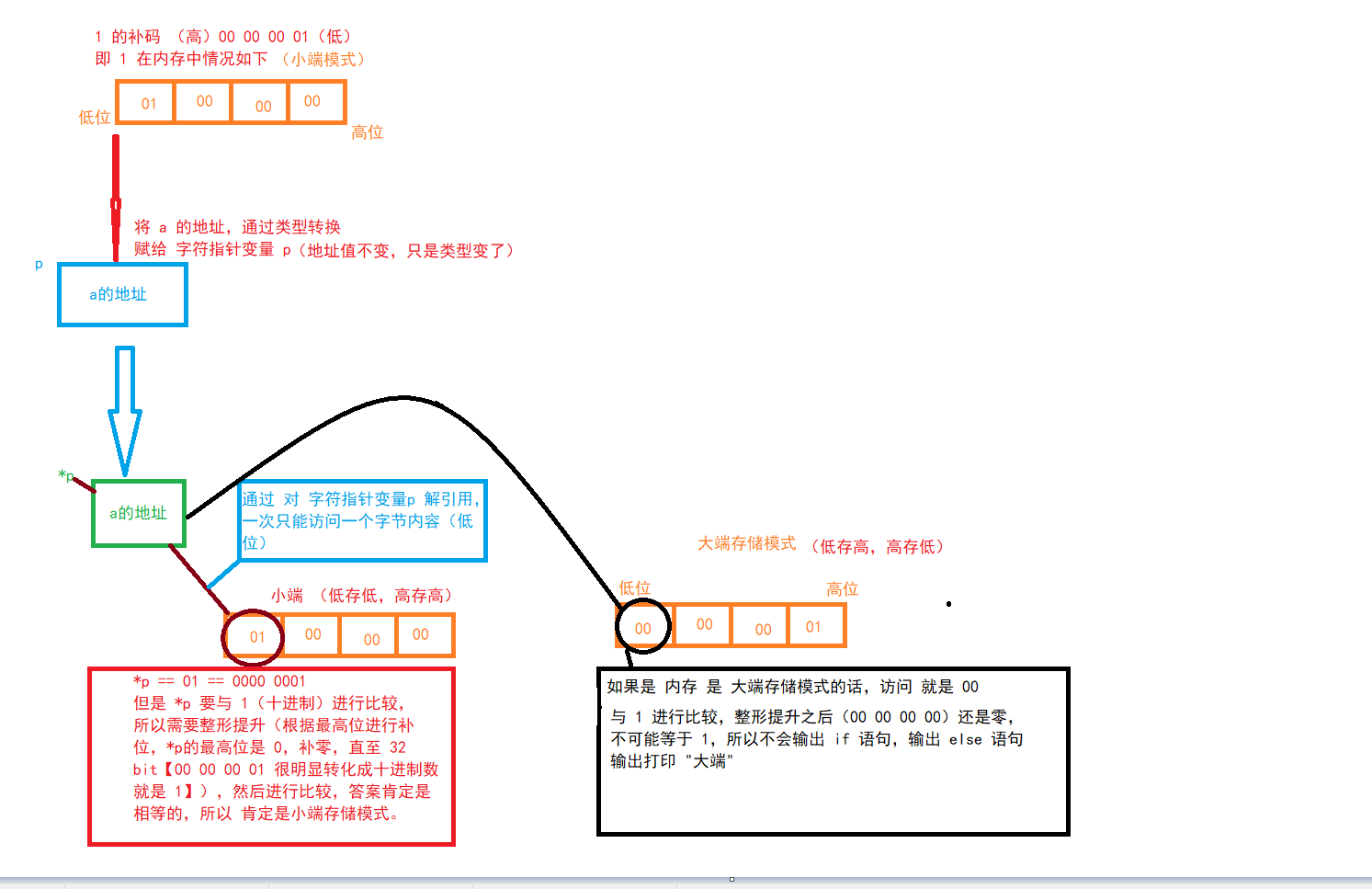
int a = 1;// 01 00 (small end storage mode)
char* p = (char*)&a; // If you want to store a in the character pointer variable p, you need to convert the address of a into a character type (the value of the address is unchanged)
if (*p == 1)
Because pointer variables p It is a character type and can only be accessed when it is dereferenced, p The content of a byte in the space pointed to by the stored address. (access is from low~From the high address,
So the first access to the first data (1 byte The content of [01] needs to be compared with 1, so it needs to be reshaped and lifted, and the bit is filled according to the highest bit [the highest bit is 0, and the zero is filled until 32 bit Bit, i.e. 00 00 01], whose value is converted to decimal number, which must be equal to 1)
{ As long as it is equal to 1, the storage mode of the compiler is small end storage mode (small end byte order storage mode)
printf("Small end\n");//So output this statement
}
else
{ If it is not equal to 1, it must be the big end storage mode
printf("Big end\n");
}
return 0;
}
Writing method 2
#include<stdio.h>
int check_sys()
{
Writing method 1
int a = 1;
return *(char*)&a;
Writing method 2
//char* p = (char*)&a;
//return *p;
Return 1 small end
Return 0 big end
}
The pointer type determines how many bytes the pointer dereference operator can access at a time, char* p ; *p Can access a byte, int*p;*p 4 bytes can be accessed
int main()
{
int ret = check_sys();
Return 1 small end
Return 0 big end
if (ret == 1)
{
printf("Small end\n");
}
else
{
printf("Big end\n");
}
return 0;
}
Example 1
vs environment
#include<stdio.h>
int main()
{
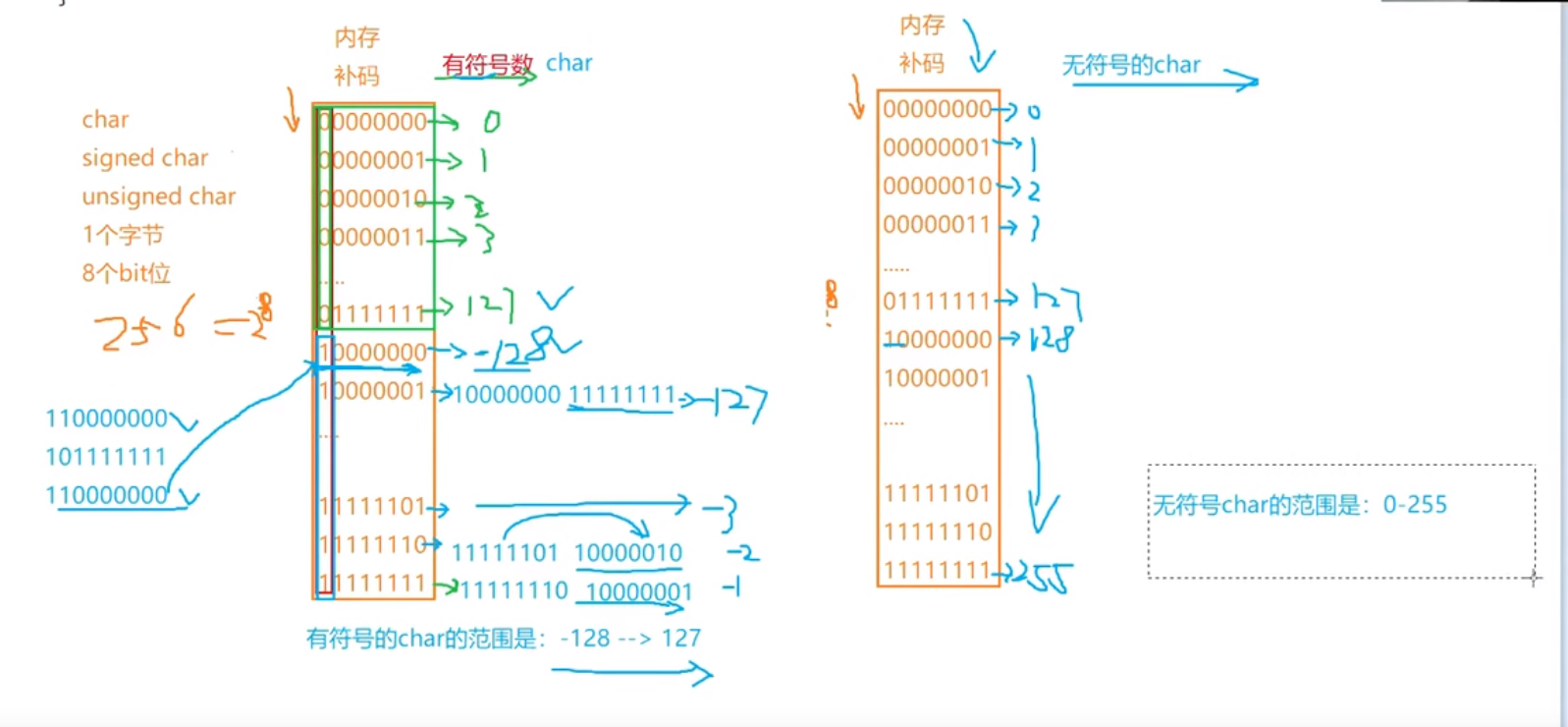
char a = -1;
100000000000000000000000 00000001 -1 Original code of
111111111111111111111111 11111110 -1 Inverse code of
111111111111111111111111 11111111 -1 Complement of
// a is signed character type data; The 8th bit of the complement is stored (data truncation, the low-order data is intercepted because it is in the small end storage mode); '"
//Before printing a, it needs to be shaped and lifted to supplement according to the symbol bit. According to the highest bit, the highest bit is 1. The complement is 32 1s, which is the complement of - 1,
//The original code is printed, so it needs to be converted into the original code, i.e. 10000000 0000000 0000000 00000001
// a outputs - 1
signed char b = -1; //Signed; 8 stored complements 1 (truncated)// Before printing, shaping and lifting (arithmetic logic) shall be supplemented according to the sign bit,
//I.e. 32 1. The original code printed is 10000000 0000000 0000000 0000000 01, i.e. - 1
unsigned char c = -1;// The unsigned number indicates that the unsigned number carries out shaping and lifting, and directly complements 0, while the complement bits of - 1 are 8 1 (truncated);
//It needs to be shaped and raised before printing: 00000000 00000000 11111111 convert it to decimal, i.e. 255
printf("a = %d,b = %d,c = %d ", a, b, c);// -1,-1,255
return 0;
}
Example 2
#include<stdio.h>
int main()
{
char a = -128;
//10000000 00000000 00000000 1000 0000; Original code
//1111111111111111111111111111111111111110111111 inverse code
//11111111111111111111111111111 1000 0000 complement
// 10 million truncation
printf("%u\n",a);//Before printing, shaping and lifting (signed number, filling according to the highest bit [1]): 11111111111111111111111 1000 0000
// %u: The printing is unsigned, so the three codes are the same. Directly convert their binary into decimal number for output (and the result is always greater than 0 [non negative number])
// The output is 4294967168
return 0;
}
Example 3
Signed and unsigned addition
#include<stdio.h>
int main()
{
int i = -20;
//10000000 0000000 0001 0100 original code
//11111111111111111111111111110 1110 1011 inverse code
//1111111111111111111111111111110 1100 complement
unsigned int j = 10;// The unsigned number is the same as three codes
//00000000 00000000 00000000 0000 1010 the original inverse complement code is the same as the three codes
//00000000 00000000 00000000 1010 J's complement
+
//1111111111111111111111111111111111110 complement of 1100 I
==
//1111111111111111111111111111111111 0110 result (complement)
//10000000 0000000 0000000 000000 1001 result (inverse code) [in addition to the sign bit, the other bits of the complement are reversed]
//10000000 00000000 00000000 1010 result (original code) [complement + 1]
Both methods can be used
11111111 11111111 11111111 1111 0101 Inverse code == Complement-1;
10000000 00000000 00000000 0000 1010 Original code == Inverse code [except the sign bit, the other bits are reversed by bit]
printf("%d\n",i+j);// Printing is to print the original code
10000000 00000000 00000000 0000 1010 The time to number is 10
return 0;
}
Example 4
#include<stdio.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);// Loop i is an unsigned number, so i can never be less than 0
}
return 0;
}
Example 5
#include<stdio.h>
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
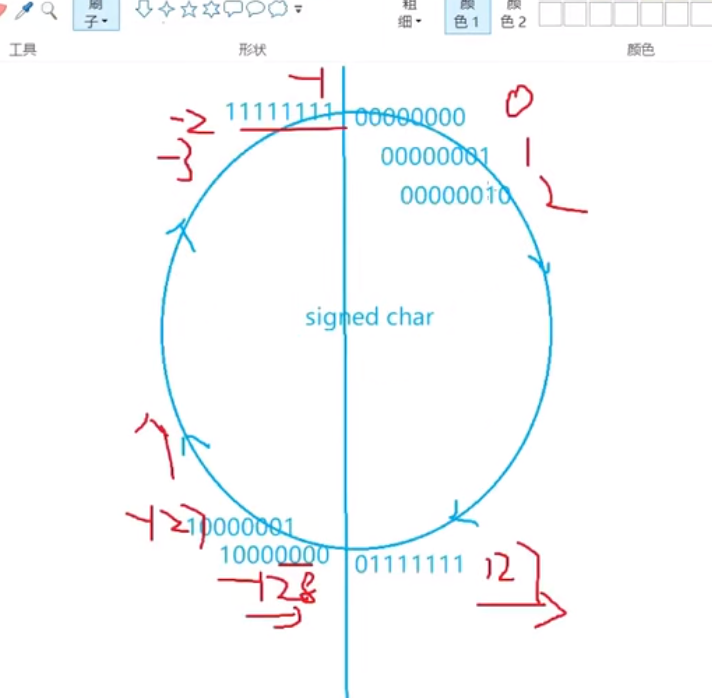
Because the data is char Type, signed range -128~127,However, there are a lot of data larger than 255, resulting in a large value
So we need to convert these 1000 numbers into -128~127,Can be put into the character array
That is, the 128th element is -128,The 129 th element is -127 By analogy, the 256 th element is 0, and the 257th element is 1. According to this mode, the assignment cycle continues until the value of 1000 elements is assigned
strlen Calculating the number of elements is logically a thousand elements, but because char Its value has a value of 1 and a value of 0, and'\0'Yes ASCII The code value is 0
,So the value he calculated could not be 1000
See the attached figure below for details. It turns clockwise, Wait until it goes to 0 == '\0'Stop when you're ready. That is, the 256 th element 0 == '\0' Will stop counting( strlen encounter'\0',Stop counting,'\0'Not counted), i.e. output 255[ strlen Counting stops when only 255 elements are counted]
return 0;
}
Attached drawings
Example 6
#include<stdio.h>
unsigned char i = 0;// Unsigned char range 0 ~ 255
int main()
{
for (i = 0; i <= 255;i++)//Constant satisfaction, so the nature of the dead cycle is the same as that of case 5. The 256 element is 0, and then it starts to increase, and then it goes back and forth.
{
printf("hello world!\n");
}
return 0;
}
Storage of floating point in memory
Procedure I:
#include<stdio.h>
int main()
{
double d = 1E10;// 1e10: 1 times 10 to the power of 10
printf("%lf\n", d); //10000000000.000000
return 0;
}
Procedure 2:
#include<stdio.h>
int main()
{
int n = 9;
float* pfloat = (float*)&n;//Forced conversion type
printf("n The value of is:%d\n",n);//The value of n is: 9
printf("pfloat Value of:%f\n",*pfloat);//The value of pfload: 0.000000. The default is 6 zeros after the decimal point
Plastic deposit, plastic take out, no problem; There is a problem with floating point
*pfloat = 9.0;
printf("n The value of is:%d\n", n);// The value of n is 1091567616
printf("pfloat Value of:%f\n", *pfloat);//Value of pfloat: 9.000000
Floating point storage, floating point take out, no problem; Plastic surgery is a problem
It is concluded from the above expression that integer and floating-point types are stored in memory in different ways
return 0;
}
n and *pfloat It's the same number. Why are the interpretation results of floating-point numbers and integers so different?
Therefore, we must understand the representation of floating-point numbers in the computer.
According to the international standard IEEE 754 (IEEE 754, which specifies how floating point types are stored in memory), any binary floating point number V can be expressed in the following form:
(-1) ^ S * M * 2 ^ E
(- 1) ^ S represents the sign bit. When S = 0, V is a positive number; When S = 1, V is negative (- 1 to the power of 0, - 1 to the power of 1)
M represents a significant number, greater than or equal to 1 and less than 2
2^E indicates exponential bit
example

IEEE 754 stipulates that for 32-bit floating-point numbers, the highest 1 bit is symbol bit S, the next 8 bits are exponent E, and the remaining 23 bits are significant digits M

IEEE 754 has some special provisions on the significant number m and index E. as mentioned earlier, 1 < = m < 2, that is, M can be written in the form of 1.xxxxxx (where XXXXXX represents the decimal part)
IEEE 754 stipulates that when M is saved in the computer, the first digit of this number is always 1 by default, so it can be rounded off
Save only the following xxxxxx Part: for example, save 1.01,Save only 01. When reading, add the first 1. This can improve the accuracy of one bit. For 32 bits, it is equivalent to saving 24 significant digits
Index E
first, E Is an unsigned integer( unsigned int)This means that if E It is 8 bits and its value range is 0~255;If E It is 11 bits, and its value range is 0~2047. However, we know that in scientific counting E Negative numbers can occur, so IEEE 754 Specified, when stored in memory E The true value of must be added with an intermediate number. For 8-bit E,The middle number is 127 for 11 bits E,The median is 1023. For example, 2 ^ 10 of E It is 10, so when saving a 32-bit floating-point number, it must be saved as 10 + 127 = 137,I.e. 1000 1001
Let's look at a little bit more
Decimal 0.5 = 0.1 (Binary representation) 0 -> 2^0 (1*0 == 0); 1 -> 2 ^ (-1) be equal to (1 * 1/2) = 0.5

Because the significant number (M) must be greater than or equal to 1 and less than 2 [1 < = M < 2],
Therefore: 1 < = m < 2, so the decimal point of 0.1 is shifted to the right, i.e. 1.0 ^ (- 1)
So (- 1) ^ S * M * 2 ^ E == (-1) * 0 * 1.0 * 2 ^ (-1)
S == 0 M == 1.0 E == -1 When saving to memory E ,Must be true(-1)Add a middle number (127). For 8-bit E,The median is 127 therefore -1 + 127 = 126 That is, the real deposit E The value (stored value) of is 126 (converted binary) 0111 1110, If you want to know E The true value of is subtracted from the intermediate value 127, i.e. 126 - 127 = -1
Examples
#include<stdio.h>
int main()
{
float f = 5.5;
// Convert floating-point number 5.5 to binary floating-point number, i.e. 101.1. Because 1 < = m < 2, the decimal point moves 2 digits to the left, so 1.011 * 2 ^ 2
Because 5.5 > 0,therefore S == 0
The expression ends with (-1) ^ 0 *1.011 * 2^2
S == 0
M == 1.011 // IEEE 754 stipulates that when saving M in the computer, the first digit of this number is always 1 by default, so it can be rounded off and only the 011 part after the decimal point is saved
E == 2 -> 2+127 = 129 -> 10000001
Single precision floating point storage model
S EEEEEEEE MMMMMMMM MMMMMMMM MMMM MMM
S ( 1 bit) E( 8 bit) M ( 23 bit )
0 10000001 01100000 00000000 0000 000// Directly fill zero after 011
0100 0000 1011 0000 0000 0000 0000 0000
4 0 b(11) 0 0 0 0 0 That is, 0 x 40 b0 00 00 Hexadecimal number
Memory form 00 00 b0 40(Small end)
return 0;
}
Index E can also be extracted from memory in three cases:
1. E is not all 0 or all 1
At this time, the floating-point number is represented by the following rule, namely index E The calculated value of (binary to decimal) minus 127 (32 bits)/ 1023(64 Bit) to get the true value. Then put the significant number M Preceded by a 1, such as 0.5( 1/2 )The binary form of is 1. 0* 2^(-1),Since it is specified that the positive part must be 1. That is, move the decimal point to the right by 1 digit, that is, 1.0 * 2^(-1),Its order code( E) by -1 + 127 = 126,Converted to binary number 0111 1110 And 1.0 After removing the integer part, there is still a 0, and the 0 to 23 bits are supplemented (supplemented later) The binary representation is 0 01111110 00000000000000000000000
2. E is all 0-0 [00000000 (E)] 0110000000000000000000000, which is equivalent to (plus or minus) ± 0.011 * 2 ^ (- 126) a number whose plus or minus is infinitely close to 0 [the plus or minus is because of the S square of (- 1)]
When E When all are 0, the exponent of the floating point number E Equal to 1-127[-126] (Or 1-1023 [-1022] )mean E Stored value of, Significant number M No, add The first 1 (because it's added, it's equal to not adding, a number of a few points, multiplied by one of the 126 powers of 2 [2^-126],It is an infinite number close to 0) Direct 0.011 * 2^(-126),The restored number is infinitely close to 0. Plus plus plus minus, it is infinitely close to 0 Instead, restore to 0. xx xx xx The decimal point (six digits after the decimal point) is used to represent +-(Positive and negative) 0,And a small number close to 0.
3. E is all 1 -- 0 {111111111} 0110000000000000000
E The stored value for is 255,[E+ 127 = 255]
E True value of 255 - 127 == 128
(Positive and negative+-)1,xxx * 2 ^ 128
At this time,If significant number M All 0 (1),0 * 2^128),express+-(Positive and negative) an infinite number (positive and negative depends on the sign bit[(-1)^S ] )
example
#include<stdio.h>
int main()
{
int n = 9;
// 00000000 00000000 0001001 complement
float* pfloat = (float*)&n;//Forced conversion type
printf("n The value of is:%d\n",n);//The value of n is: 9
printf("pfloat Value of:%f\n",*pfloat);//The value of pfload: 0.000000. The default is 6 zeros after the decimal point
Single precision floating point storage model
S EEEEEEEE MMMMMMMM MMMMMMMM MMMM MMM
S ( 1 bit) E( 8 bit) M ( 23 bit )
9 The complement of is 0 00000000 0000000000000000001001
Meet the above conditions 2 E All zero
// That is, 0.000000 0000000000001001 * 2 ^ - 126 is a number whose positive and negative are infinitely close to 0. Floating point data retains 6 digits after the decimal point by default
*pfloat = 9.0;
// 1001.0
//-1 ^ 0 * 1.001 * 2 ^ 3 E= 3 + 127 =130[10000010]
// 0 10000010 001 00000000000000000000
//Positive number 2 ^ 24 + 2 ^ 20 + 2 ^ 30 = = 1091567616
printf("n The value of is:%d\n", n);// The value of n is 1091567616
printf("pfloat Value of:%f\n", *pfloat);//Value of pfloat: 9.000000
return 0;
}