#Data structure and algorithm Introduction
There is no best algorithm in the world, only the most suitable algorithm


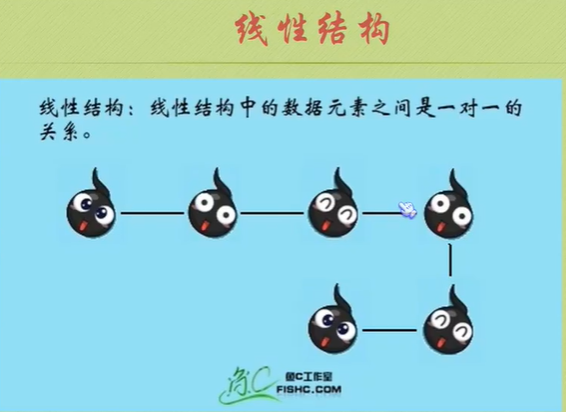
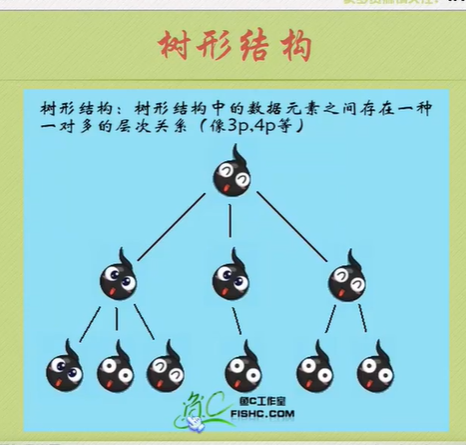
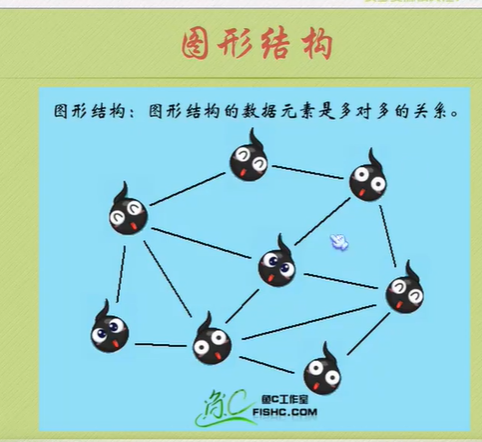
Logical structure

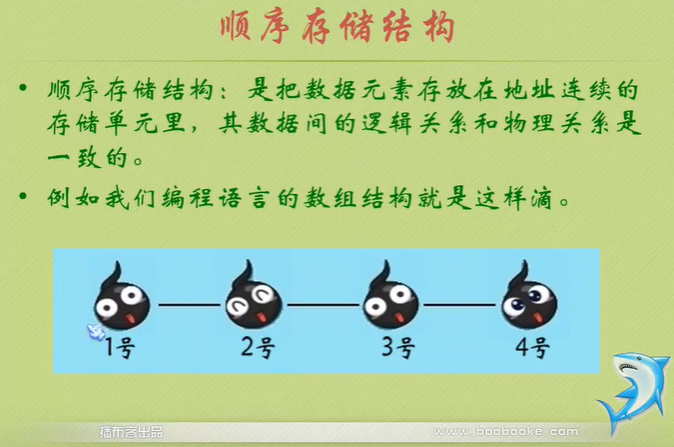
Physical structure



Talk about algorithm









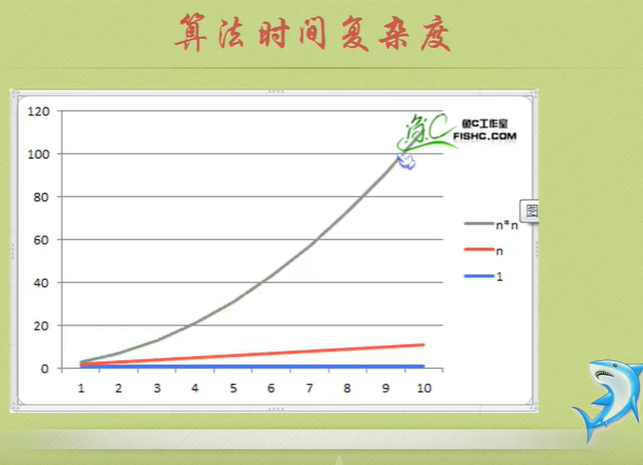
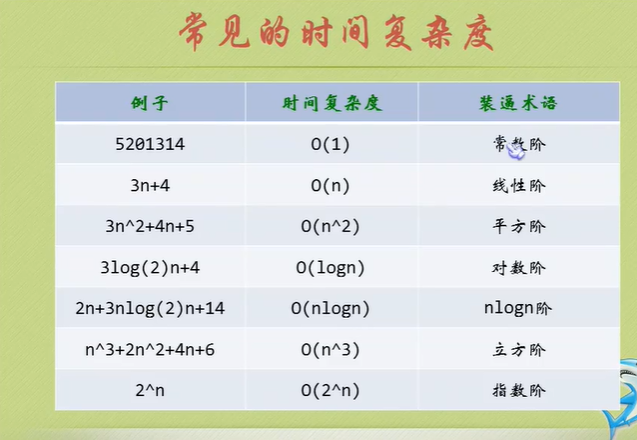
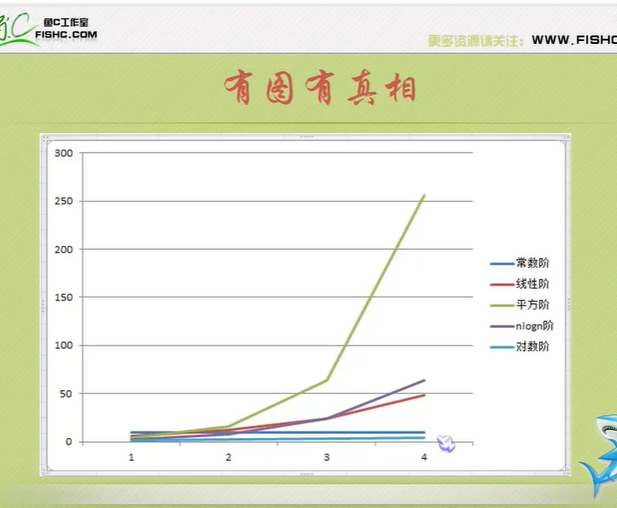
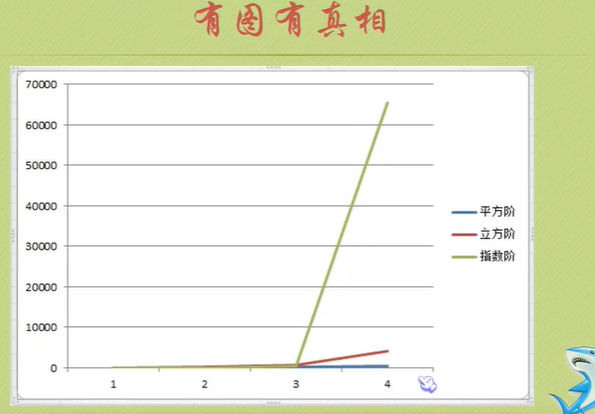
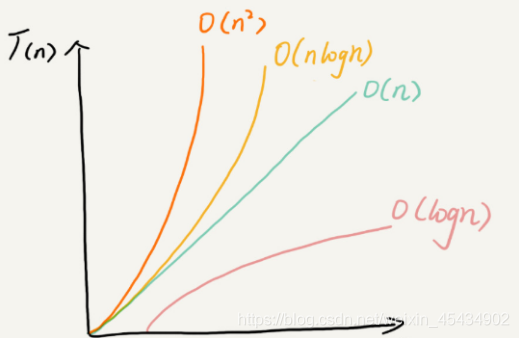
Algorithm time complexity




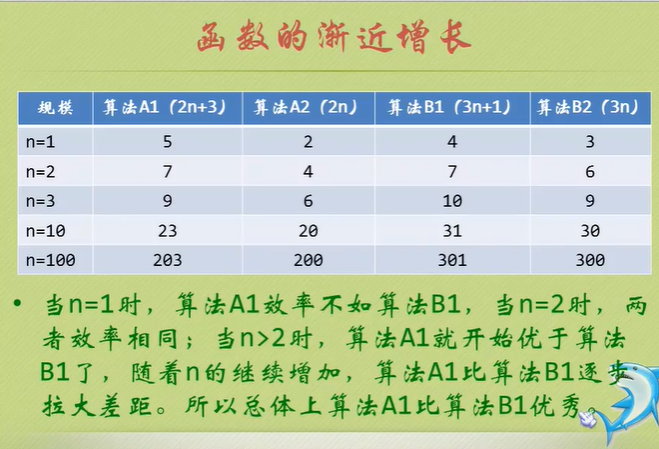
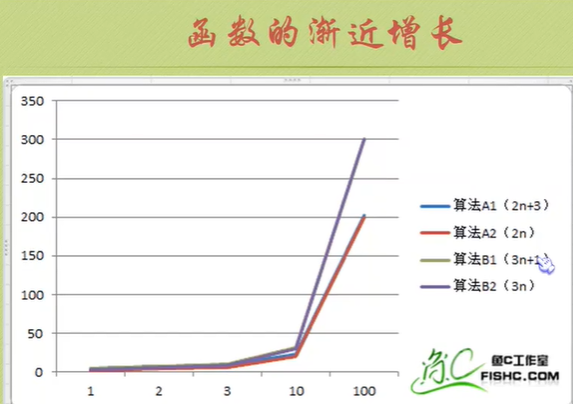

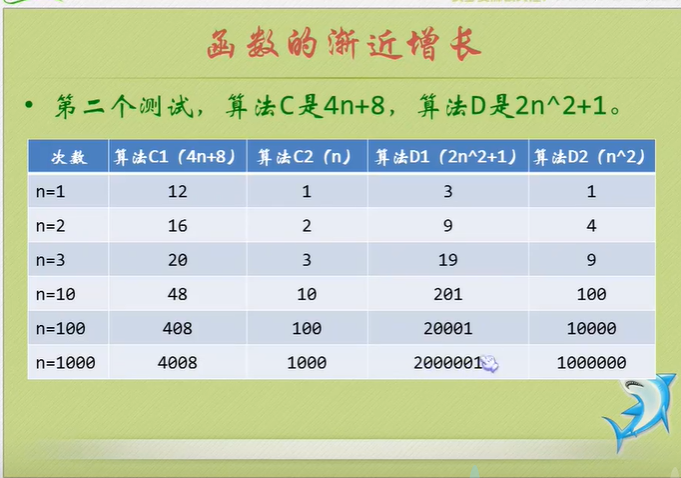
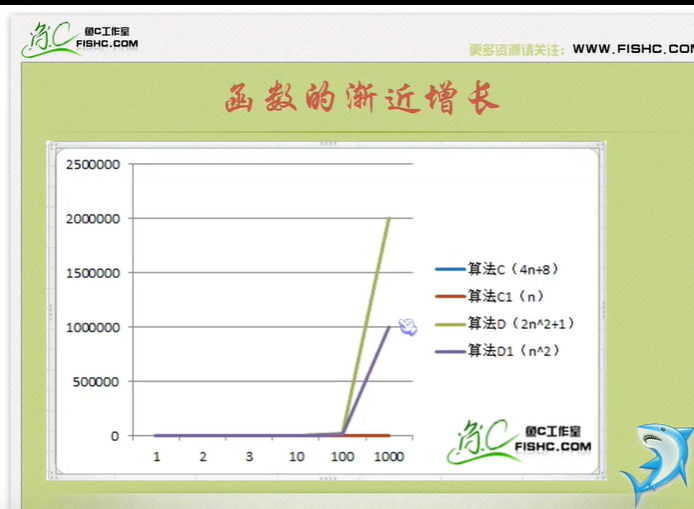

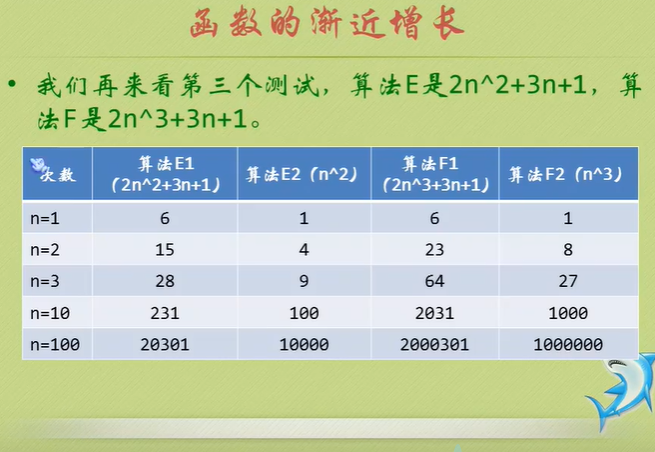
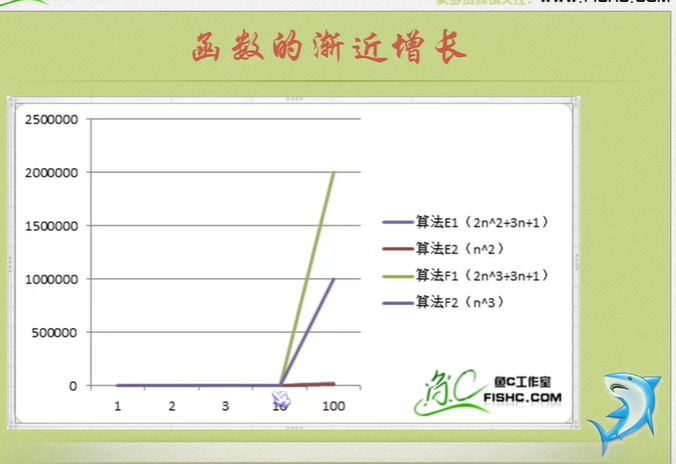

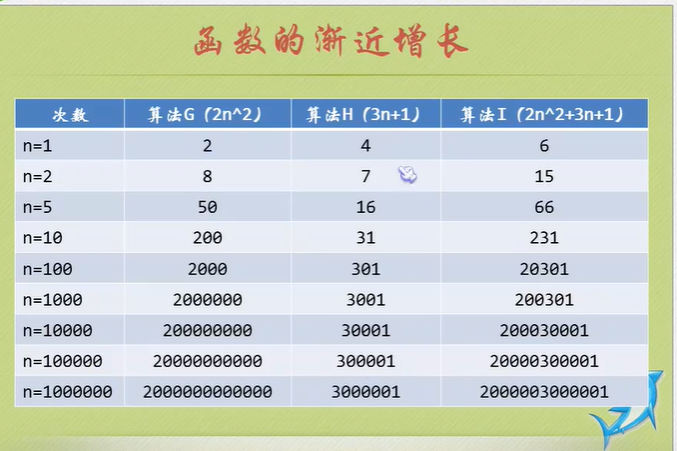
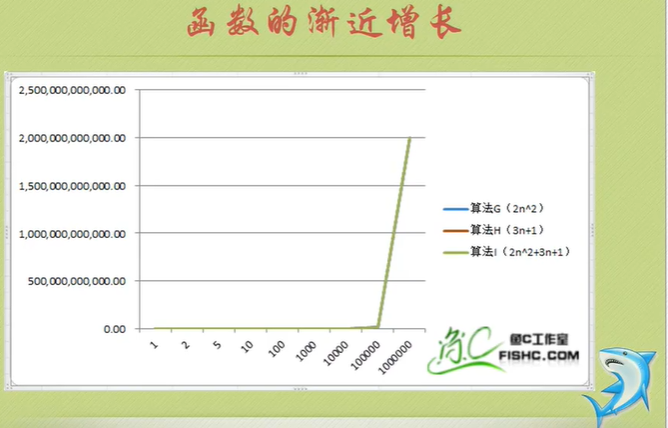
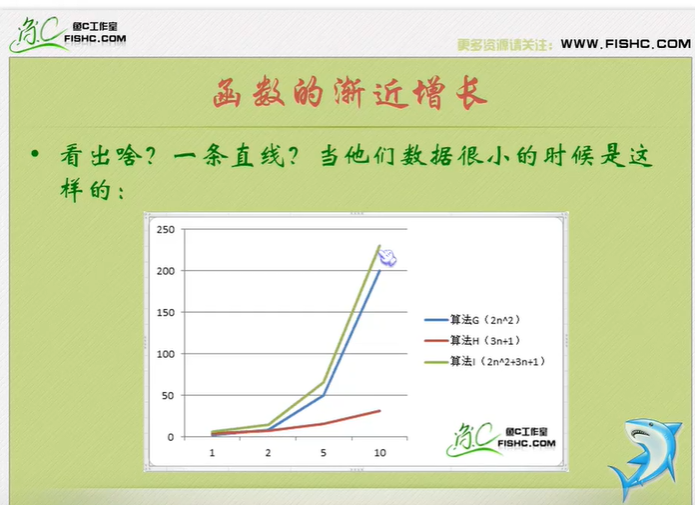

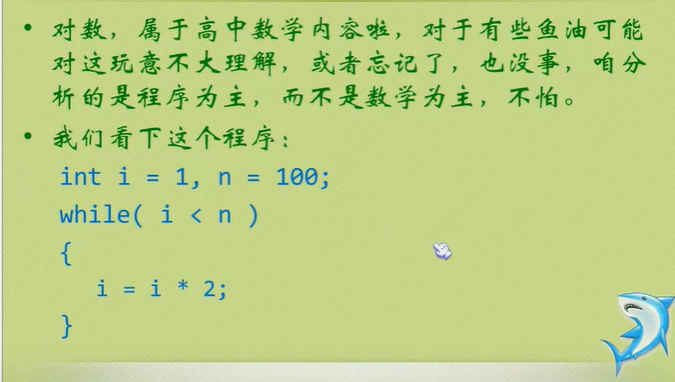
Just tell you to pay attention to the highest order, then ignore the constant product of constant and order, and pay attention to enough data.

The number of executions is the time

















Algorithm space complexity



Linear table





Abstract data type










void unionL(List* La, List* Lb)//This pseudo code is to insert data different from La in Lb into La in turn
{
int La_len, Lb_len, i;
ElemType e;
La_len = ListLength(*La);
Lb_len = ListLength(*Lb);
for (int i=1;i<=Lb_len;i++)//This is written as a data structure algorithm, because the focus is on the algorithm process, not let the compiler understand it
{
GetElem(Lb, i, &e);
if (!Locate(*La,e))
{
ListInsert(La, ++La_len, e);
}
}
}
Sequential storage structure of linear table



Address calculation method


This should be O(1), not 0 (1).
Get element operation


typedef int Status;
Status GetElem(Sqlist L,int i,ElemType *e)
{
if (L.length == 0 || i<i || i>L.length)//The linear table starts with 1
{
return ERROR;
}
*e = L.data[i - 1];
return OK;
}
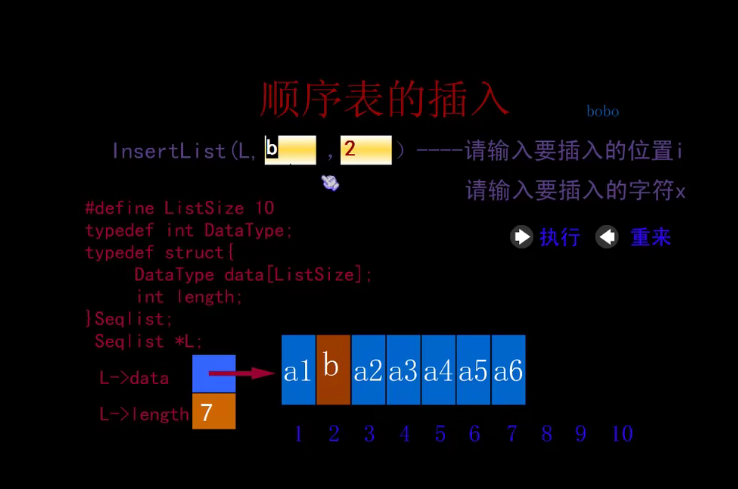
Insert operation



Status ListInsert(Sqlist *L, int i, ElemType e)
{
int k;
if (L->length == MAXSIZE)//The sequence table is full
{
return ERROR;
}
if (i<1 || i>L->length + 1)//i out of range
{
return ERROR;
}
if (i <= L->length)
{
for (k = L.length - 1; k >= i - 1; k--)
{
L->data[k + 1] = L->data[k];//Element backward
}
}
L->data[i - 1] = e;
L->length++;
return OK;
}
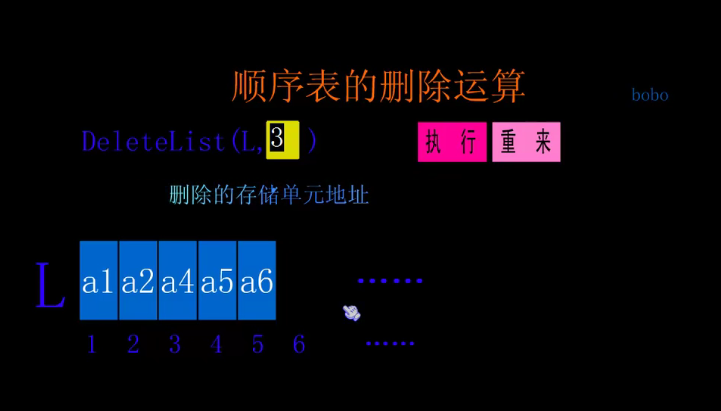
Delete operation

//delete
//Output the i th element of L and use e to return the deleted value.
Status ListDelete(Sqlist* L, int i, ElemType e)
{
if (L - length == 0)
{
return ERROR;
}
if (i<1 || i>L->length )//i out of range
{
return ERROR;
}
e = L->data[i - 1];
if (i <= L->length)
{
for (k = i; k < L->length; k++)
{
L->data[k - 1] = L - data[k];
}
}
L->length--;
return e;
}

Advantages and disadvantages of linear table sequential storage structure


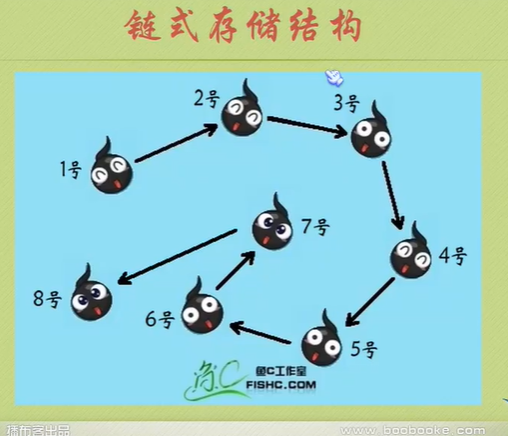
Chain storage structure of linear list



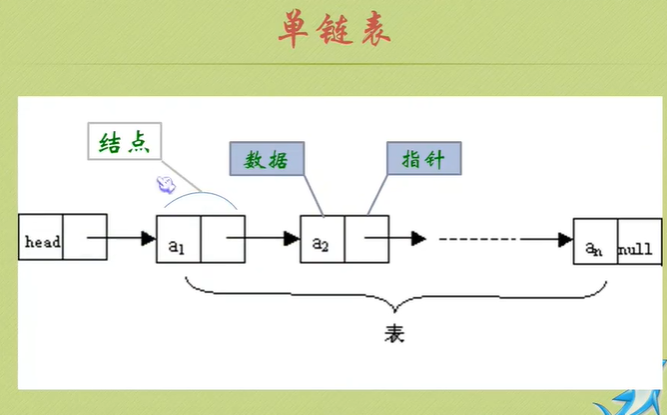
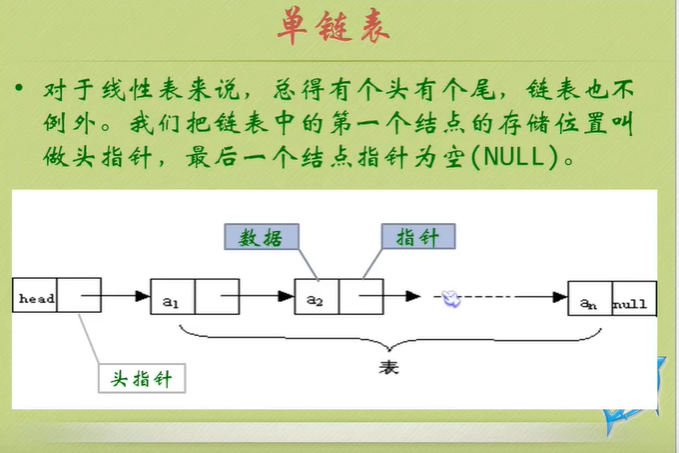

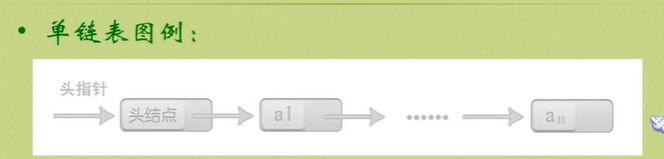
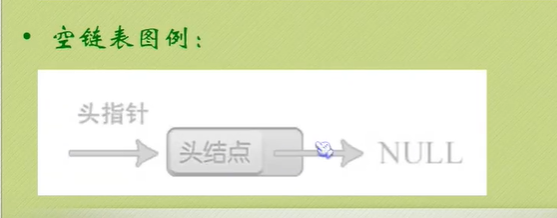
You can see that the null pointer points to the header node.
The node behind the head node is the one that really stores data.



Single linked list reading

//obtain
Satus GetElem(LinkList *L, int i, ElemType* e)
{
int j;
LinkList p;
p = L->next;//p points to the first node
j = 1;
while (p && j < i)//When jumping out of the loop, normally it should be i==j
{
p = p->next;
++j;
}
if (p! || j > i)//If p points to null or what you want to find doesn't exist at all
{
return ERROR;
}
*e = p->data;
return OK;
}

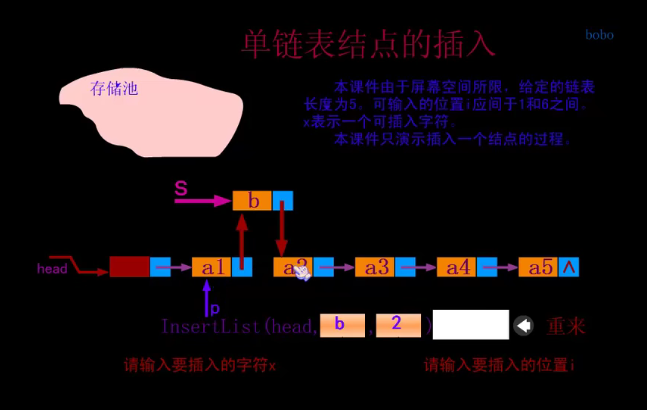
Single linked list insert
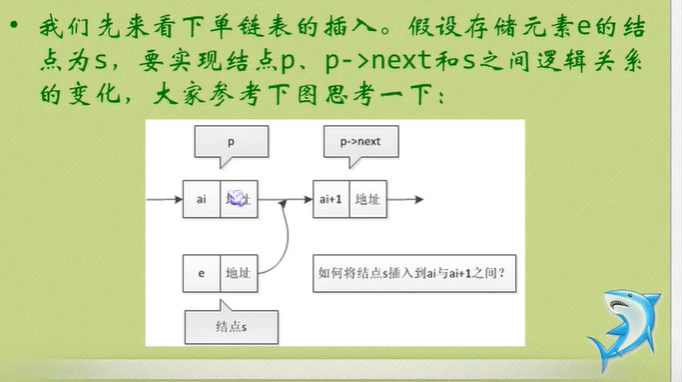


//Single linked list insert
//Insert a new element e after the ith position in L, the length of L plus 1
Status ListInsert(LinkList* L, int i, ElemType* e)
{
int j;
LinkList* p;
LinkList* s;
p = L->next;//p points to the first node
j = 1;
while (p && j < i)//When jumping out of the loop, normally it should be i==j
{
p = p->next;
++j;
}
if (p!|| j > i)//If p points to null or what you want to find doesn't exist at all
{
return ERROR;
}
s = (LinkList)malloc(sizeof(Node));//Allocate a memory space to the new node S
s->data = *e;
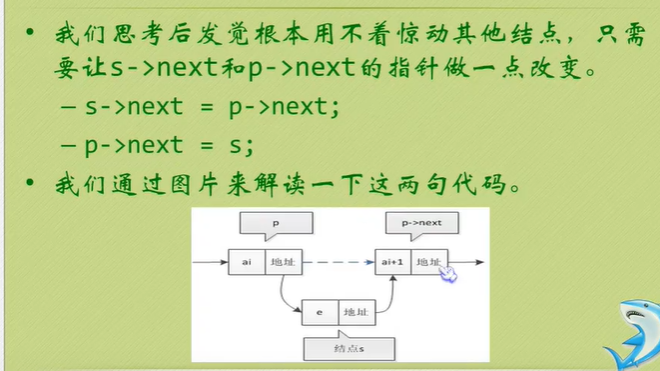
//The following two sentences must not be written backwards. The consequences were ptt mentioned earlier.
s->next = p->next;
p->next = s;
return OK;
}
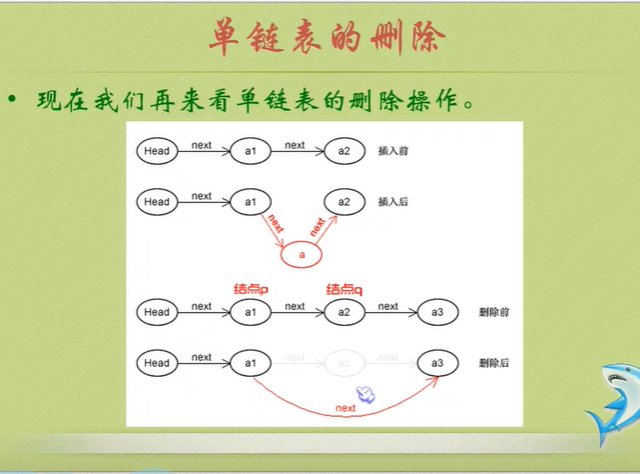


//Single linked list deletion
//Delete the ith Node and return the data in it
Status ListDelete(LinkList* L, int i, ElemType* e)
{
int j;
LinkList* p;
LinkList* q;
p = L->next;//p points to the first node
j = 1;
while (p && j < i-1)//When jumping out of the loop
{
p = p->next;
++j;
}
if (p!|| j > i)//If p points to null or what you want to find doesn't exist at all
{
return ERROR;
}
q = p->next;//q points to the ith node
p -> next = q -> next;
*e = q->data;
delete q;
return OK;
}
Efficiency PK


It can be seen that the advantages of single linked list in inserting and deleting multiple data are significantly greater than that of sequential storage structure.
Whole table creation of single linked table


Establishing single linked list by head interpolation

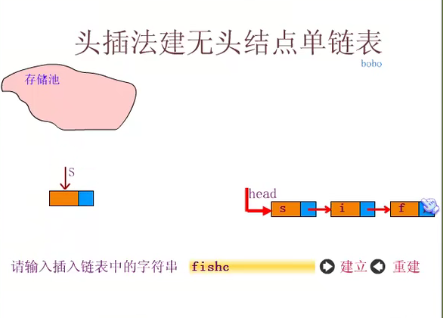
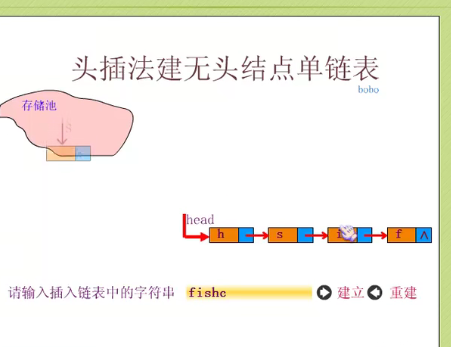
Insert the code slice here
//Single chain meter insertion
void CreateListHead(LinkList* L, int n)
{
LinkList p;
int i;
srand(time(0));//Initialize random number seed
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
for (int i = 0; i < n; i++)
{
p = (LinkList)malloc(sizeof(Node));//Generate new node
p->data = rand() % 100 + 1;
p->next = (*L)->next;
(*L)->next = p;
}
}
//Why is * l and the other is p, which means that l is a secondary pointer and the function passes in * L. we directly think that * l is a pointer to the linked list
//This code is header insertion, but the header * L is still at the front.
Code flow chart
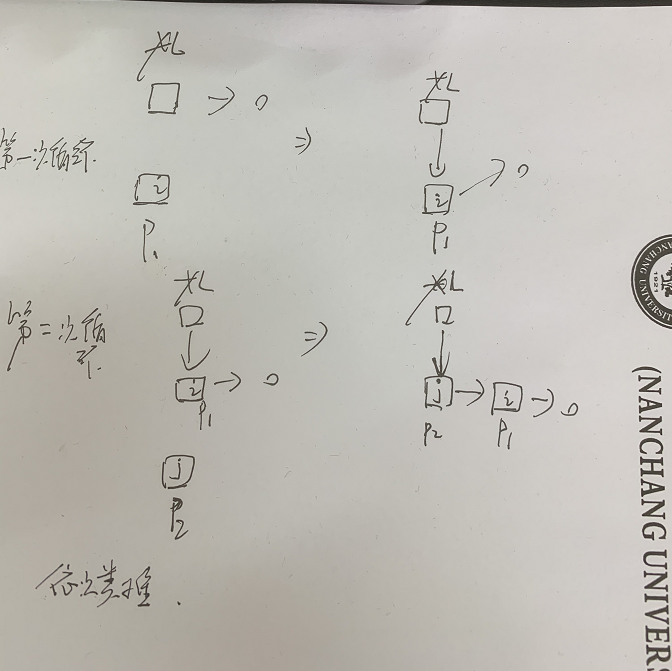
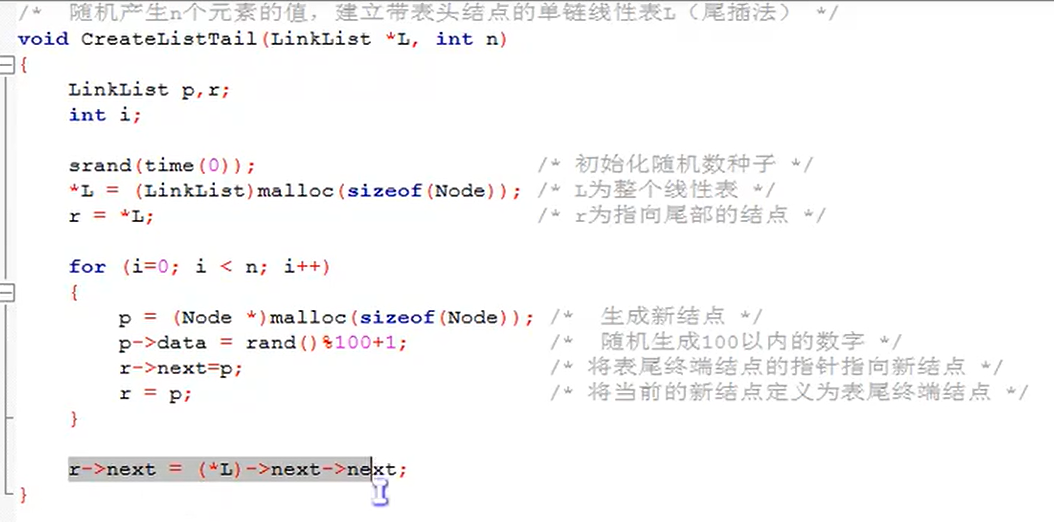
Establishing single linked list by tail interpolation

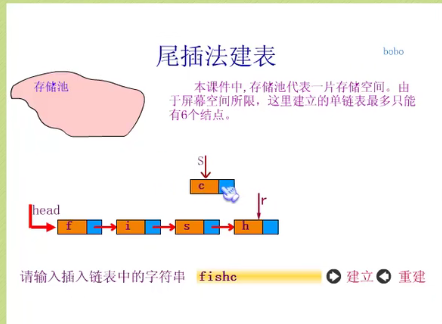
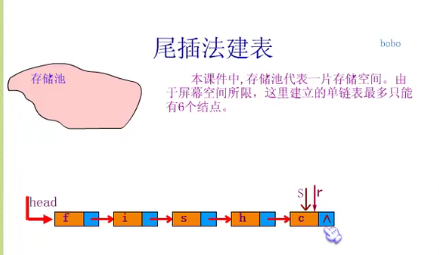
//Single chain table tail insertion
void CreateListTail(LinkList* L, int n)
{
LinkList p,r;
int i;
srand(time(0));//Initialize random number seed
*L = (LinkList)malloc(sizeof(Node));
r = *L;
for (int i = 0; i < n; i++)
{
p = (Node *)malloc(sizeof(Node));//Generate new node
p->data = rand() % 100 + 1;
r->next = p;
r = p;
}
r->next = NULL;
}
Code flow
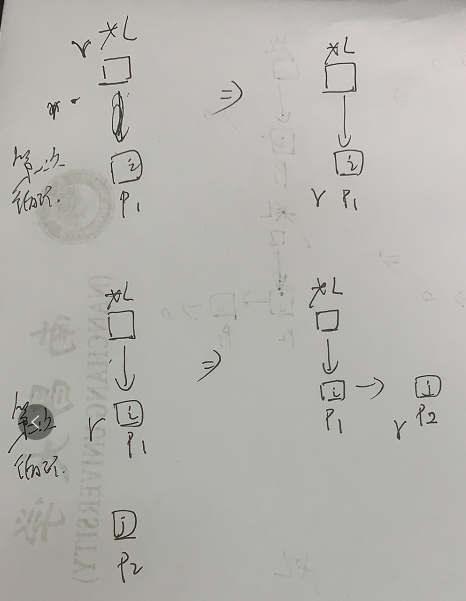
Whole table deletion of single linked list

//Single linked list whole table deletion
Status ClearList(LinkList* L)
{
LinkList p, q;
p = (*L)->next;//p points to the first node
while (p)
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL;
return OK;
}

Advantages and disadvantages of single linked list structure and sequential storage structure


For the search, the sequential storage structure has a subscript, which can be found at once. The single linked list should be found one by one, because the address of the next node should be found from the next of the previous node.
Insertion and deletion are obvious, because the sequential storage structure needs to shift other elements, while the single linked list only needs to move the pointer to.



review
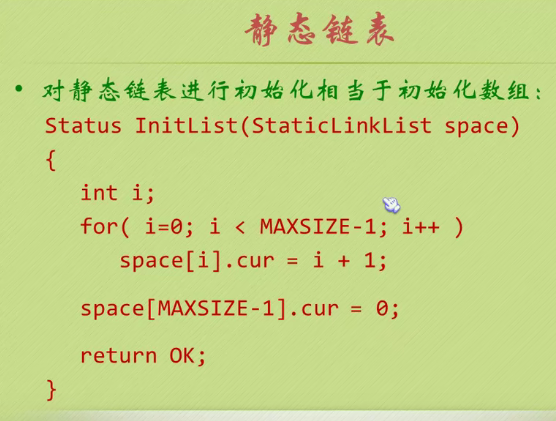
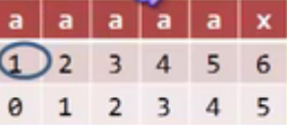
Static linked list






The cursor points to the next subscript

The cursor of the first space points to the subscript of the free space.
That is, at first, the cursor in the first space is 5, that is, the space with subscript 5 is idle, and then the cursor in the first space becomes 6
The cursor for the last non free space is represented by 0


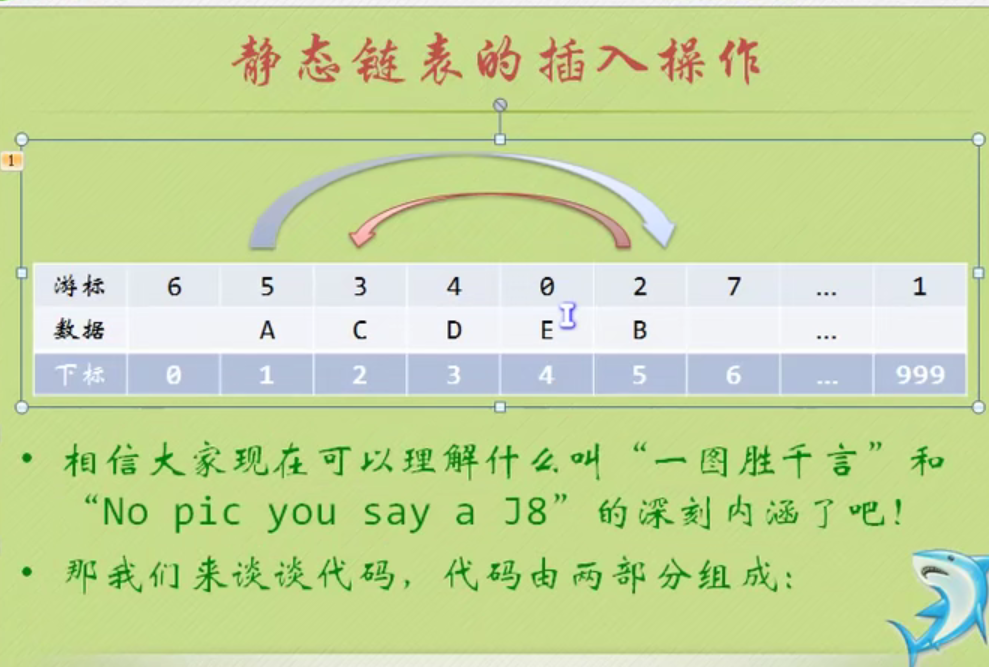
Insertion of static linked list
First, get the subscript of the free element

//Insert a new element e before the ith element in the static linked list L
//It's a little difficult to understand the code. It's better to understand it in combination with the following figure
Status ListInsert(StaticLinkList L.int i,ElemType e)
{
int j, k, l;
k = MAX_SIZE - 1;//The last element, and the cursor of the last element is the subscript of the first element
if (i<1 || i>ListLength(L)+1)//i out of normal range
{
return ERROR;
}
j = Mlloc_SLL(L);//Gets the subscript of the free element
if(j)
{
L[j].data = e;
for (l=1;l<=i-1;l++)
{
k = L[k].cur;
}
L[j].cur = L[k].cur;
L[k].cur = j;
return OK;
}
return ERROR;
}
Code flow
Take i=2 as an example




Deletion of static linked list
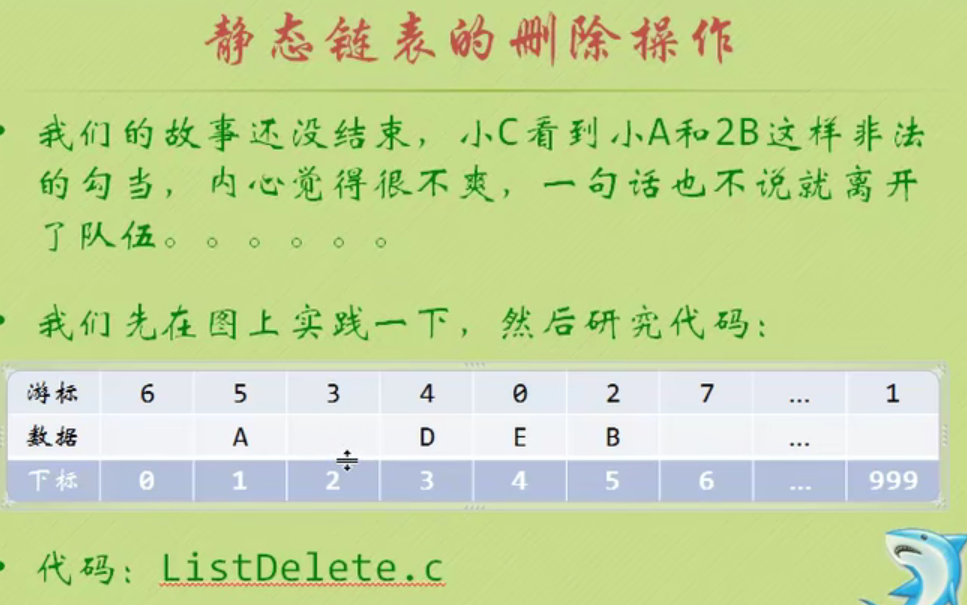


//Delete the ith element in L
Status ListDelete(StaticLinkList L.int i)
{
int j, k;
if (i<1 || i>ListLength(L) + 1)//i out of normal range
{
return ERROR;
}
k = MAXSIZE - 1;
for (j = 1; j <= i - 1; j++)
{
k = L[k].cur;//k1 =1.k2=5
}
j = L[k].cur;//j=2
L[k].cur = L[j].cur;//L[5].cur=3
Free_SLL(L.j);//Here is to connect the spare free elements
return OK;
}
//Idle nodes with subscript k will be affected by the standby linked list
void Free_SLL(StaticLinkList space,int k)
{
space[k].cur = space[0].cur;
space[0].cur = k;
}
//Returns the number of elements in L
int ListLength(StaticLinkList L)
{
int j = 0;
int i = L[MAXSIZE - 1].cur;
while (i)
{
i = L[i].cur;
j++
}
rturn j;
}
Code flow





Advantages and disadvantages of static linked list

Summary of single linked list Tencent interview questions


//Tencent interview questions, find the middle node
Status GetMidNode(LinkList L.ElemType* e)
{
LinkList search, mid;
search = mid = L;
while (search->next!=NULL)
{
if (search->next->next != NULL)
{
search = search->next->next;
mid = mid->next;
}
else
{
search = search->next;
}
}
*e = mid->data;
return OK;
}

Circular linked list

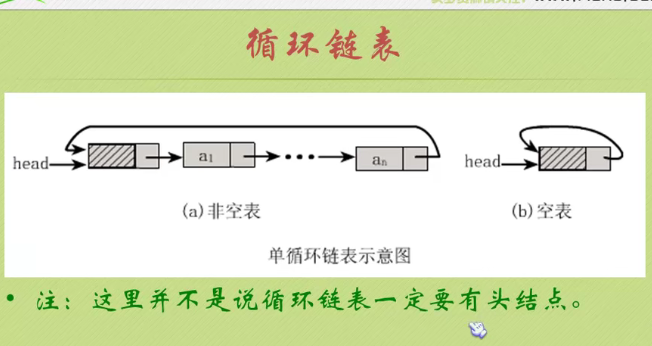


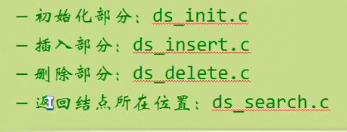
//Circular linked list
#include<iostream>
namespace xunhuanLinkList
{
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;
typedef struct cLinkList
{
int data;
struct cLinkList * next;
}node;
/*
*Insert node
* Parameters: the first node of the linked list, the insertion position
*/
void ds_insert(node **pNode,int i)
{
node *temp;
node* target;
node* p;
int item;
int j = 1;
cout<<"Enter the value of the node to insert"<<endl;
cin >> item;
if (i == 1)
{//The newly inserted node acts as the first node
temp= (node*)malloc(sizeof(struct cLinkList));
if (!temp)
{
exit(0);
}
temp->data = item;
//Find the last node
for (target = (*pNode); target->next != (*pNode); target = target->next)
;
temp ->next = (*pNode);
target->next = temp;
*pNode = temp;//The first node becomes temp
}
else
{
target = *pNode;
for (; j < (i - 1); ++j)
{
target = target->next;
}
//target points to the i-1 element
temp = (node*)malloc(sizeof(struct cLinkList));
if (!temp)
{
exit(0);
}
temp->data = item;
p = target ->next;//Point to the original i-th element
target->next = temp;//The next of the i-1 element points to the new i-th element
temp->next = p;//The new ith element points to the original ith element
}
}
/*
* Delete node
* Parameter: the first node of the linked list, the location of deletion
*/
void ds_delete(node** pNode, int i)
{
node* temp;
node* target;
int j = 1;
if (i == 1)
{//Delete first node
//Find the last node
for (target = (*pNode); target->next != (*pNode); target = target->next)
;
temp = *pNode;
*pNode = (*pNode)->next;
target->next = *pNode;
free(temp);
}
else
{
target = *pNode;
for (; j < (i - 1); ++j)
{
target = target->next;
}
temp = target->next;//
target->next = temp->next;
free(temp);
}
}
/*
* search Returns the location of the node value
* Parameter: the value of the linked list returned by the first node of the linked list
*/
int ds_search(node* pNode, int elem)
{
node* target;
int i = 1;
for (target = pNode; target->data != elem && target->next != pNode; ++i)
{
target = target->next;
}
if (target->next != pNode)//I think there is a problem, because when target - > next = = pnode, it can also target - > data = = elem
//if(target->data == elem)
{
return i;//The element does not exist in the table
}
else if(target->next == pNode &&target->data==elem)
{
return i;
}
else
{
return 0;
}
}
/*
* ergodic
* Parameter: the first node of the linked list
*/
void ds_traverse(node *pNode)
{
node* temp;
temp = pNode;
cout<<""<<endl;
do
{
cout<<temp->data<<endl;
} while ((temp = temp->next) != pNode);
cout<<endl;
}
/*
* //Initialize linked list
* Parameter: the first node of the linked list
*/
void ds_init(node **pNode)
{
int item;
node *temp;
node* target;
cout<<"Enter the value of the node and enter 0 to complete the initialization"<<endl;
while (1)
{
cin >> item;
fflush(stdin);//Clear buffer
if (item == 0)
{
return ;
}
if ((*pNode) == NULL)
{//There is only one node in the circular linked list
//There is no header node in this code. The header node is the first node, which also stores values
*pNode = (node*)malloc(sizeof(struct cLinkList));
if (!(*pNode))//*Exit if pNode is empty
exit(0);
(*pNode)->data = item;
(*pNode)->next = *pNode;
}
else
{
//Find the last node
for (target = (*pNode); target->next != (*pNode); target = target->next)
;
temp = (node*)malloc(sizeof(struct cLinkList));
//Generate a new node
if (!item)
exit(0);
temp->data = item;
temp->next = *pNode;
target->next = temp;
}
}
}
void test()
{
node* pHead = NULL;
char opp;
int find;
int search;
cout<< "1.Initialize linked list"<<endl;
cout << "2.Insert node" << endl;
cout << "3.Delete node" << endl;
cout << "4.Return node location" << endl;
cout << "5.Traversal node" << endl;
cout << "0.sign out" << endl;
cout << "Please select your action" << endl;
while (opp!='0')
{
cin >> opp;
switch (opp)
{
case '1':
ds_init(&pHead);//
cout<<endl;
ds_traverse(pHead);
break;
case '2':
cout<<"Please enter the location (node number) to insert:"<<endl;
cin>>find;
ds_insert(&pHead,find);//
cout<<endl;
ds_traverse(pHead);
break;
case '3':
cout<<"Please enter the location (node number) to delete:"<<endl;
cin>>find;
ds_delete(&pHead,find);//
cout<<endl;
ds_traverse(pHead);
break;
case '4':
cout<<"Please enter the value to query:"<<endl;
cin>>find;
search=ds_search(pHead,find);
cout<<"Found"<<find<<"The position of the is in the second"<<search<<"Nodes"<<endl;
cout<<endl;
ds_traverse(pHead);
break;
case '5':
ds_traverse(pHead);
break;
case '0':
exit(0);
}
}
}
}
int main()
{
xunhuanLinkList::test();
}
josephus problem



#include <iostream>
//josephus problem
namespace josephus
{
#include<stdlib.h>
#include<stdio.h>
#include <iostream>
using namespace std;
typedef struct node
{
int data;
struct node *next;
}node;
node* creat(int n)
{
node* p = NULL, * head;
head = (node*)malloc(sizeof(node));
p = head;
node* s;
int i = 1;
if (0 != n)
{
while (i<=n)
{
s= (node*)malloc(sizeof(node));
s->data = i++;
p->next = s;
p = s;
}
s->next = head->next;//S - > next is the first node
}
free(head);//No need to release header node
return s->next;
}
void test()
{
int n = 41;
int m = 3;
int i;
node* p = creat(n);
node* temp;
m %= n;
while (p!=p->next)
{
for (i = 1; i < m - 1; i++)
{
p = p->next;
}
cout<<p->next->data<<"->";
temp = p->next;
p->next = temp->next;
free(temp);
p = p->next;
}
cout << p->data << endl;
}
}
int main(int argc, char** argv)
{
josephus::test();
return 0;
}
Characteristics of circular linked list

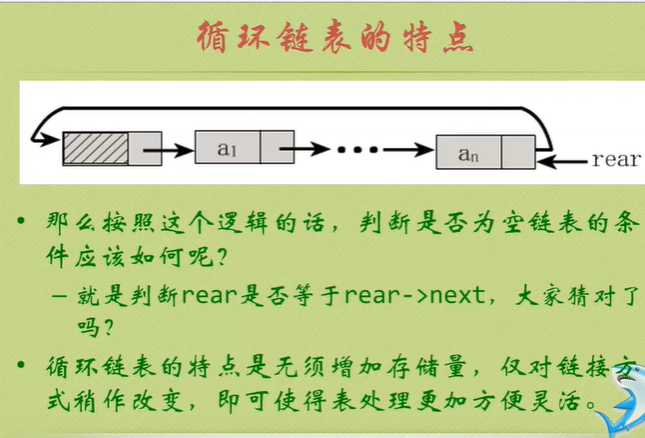

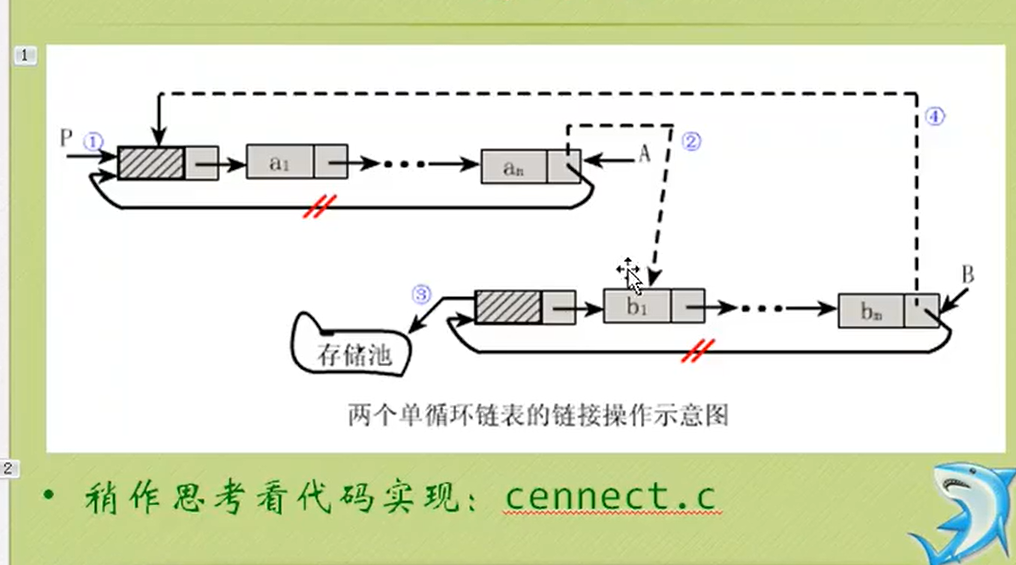
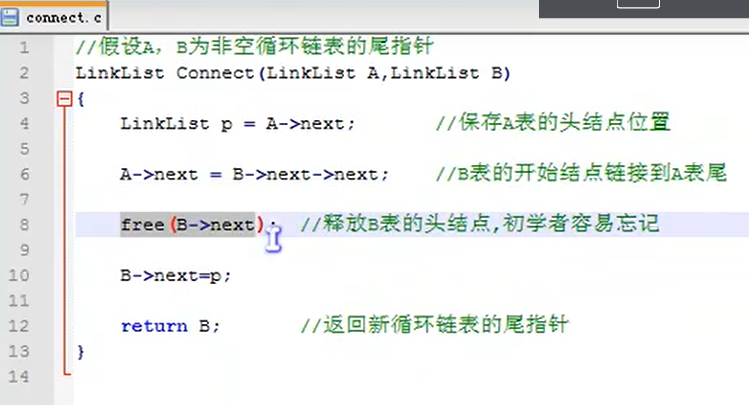
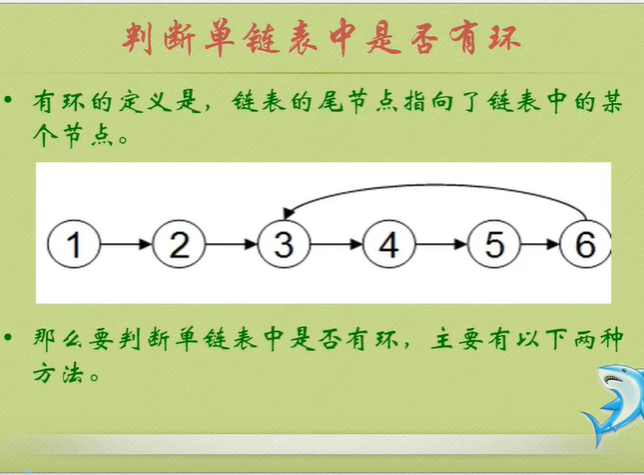
Determine whether the linked list has a ring


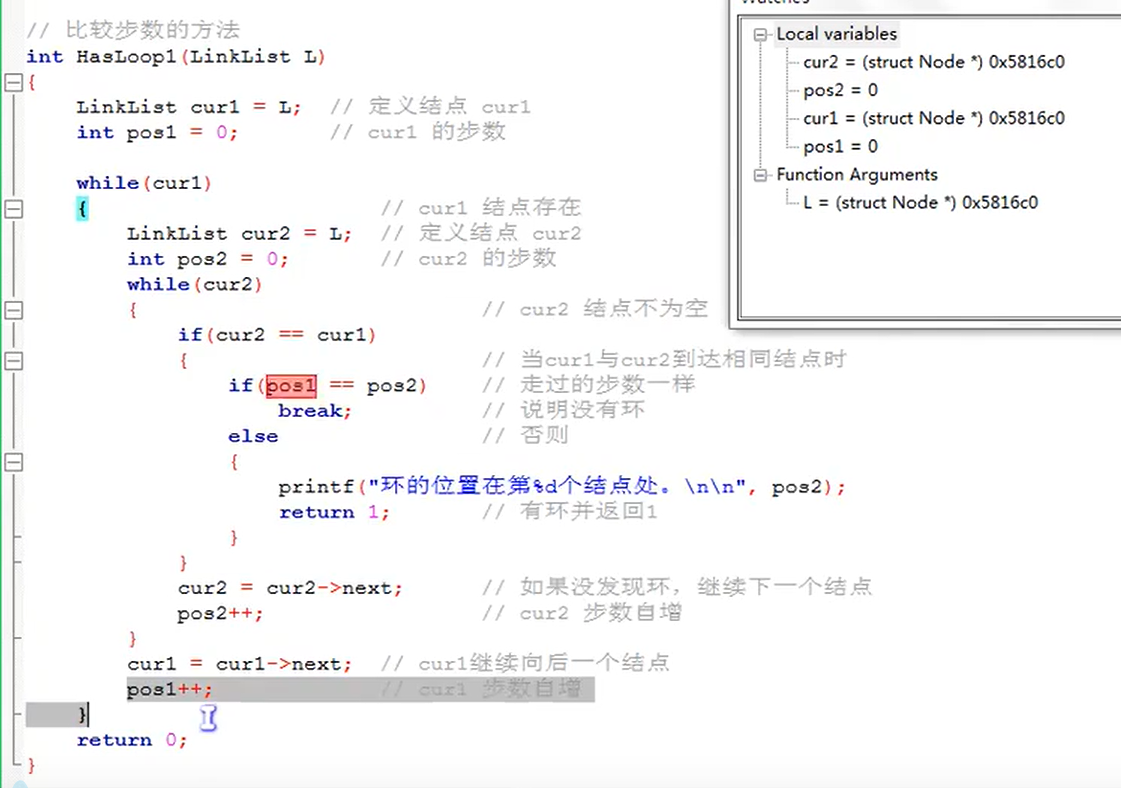
Code implementation of two methods


Overall code - not yet completed
#include<stdio.h>
#include<stdlib.h>
#include <time.h>
#include<iostream>
using namespace std;
typedef struct Node
{
int data;
struct Node * next;
}Node;
typedef struct Node *LinkList;//It means that what is defined by LinkList is a pointer
//Single chain meter insertion acyclic
void CreateListHead(LinkList * L, int n)
{
LinkList p;
int i;
srand(time(0));//Initialize random number seed
*L = (LinkList)malloc(sizeof( Node));
(*L)->next = NULL;
for (int i = 0; i < n; i++)
{
p = (Node *)malloc(sizeof(Node));//Generate new node
p->data = rand() % 100 + 1;
p->next = L->next;
(*L)->next = p;
}
}
int main() {
std::cout << "Hello, World!" << std::endl;
return 0;
}
Magician deal






The code is as follows:
#include <iostream>
#include<stdio.h>
#include<stdlib.h>
using namespace std;
static int CardNumber=13;
typedef struct Node
{
int data;
struct Node * next;
}sqlist,*LinkList;
typedef struct Node *LinkList;//It means that what is defined by LinkList is a pointer
/**
* Generation of circular linked list
*/
LinkList CreatLinkList()
{
LinkList head=NULL;
LinkList s ,r;
int i;
r=head;
for(int i=0;i<CardNumber;i++)
{
s=(LinkList) malloc(sizeof (sqlist));
s->data=0;
if(head==NULL)
head=s;
else
r->next=s;
r=s;
}
r->next=head;
return head;
}
/**
* Destruction work
*/
void DestoryList(LinkList *List)
{
LinkList ptr=*List;
LinkList buff[CardNumber];
int i=0;
while (i<CardNumber)
{
buff[i++]=ptr;
ptr=ptr->next;
}
for(i=0;i<CardNumber;i++)
{
free(buff[i]);
}
*List=0;
}
/**
* Licensing sequence calculation
* @return
*/
void Magician(LinkList head)
{
LinkList p;
int j;
int Countnumber=2;
p=head;
p->data=1;
while (1)
{
for(j=0;j<Countnumber;j++)
{
p=p->next;
if(p->data!=0)//If there is a card in this position, the next position
{
p->next;//p=p->next;??
j--;
}
}
if(p->data==0)
{
p->data=Countnumber;
Countnumber++;
if(Countnumber==14)
break;;
}
}
}
int main() {
LinkList p;
int i;
p=CreatLinkList();
Magician(p);
cout<<"In the following order:"<<endl;
for(i=0;i<CardNumber;i++)
{
cout<<"spade"<<p->data;
p=p->next;
}
DestoryList(&p);
return 0;
}
Latin matrix problem - assignment

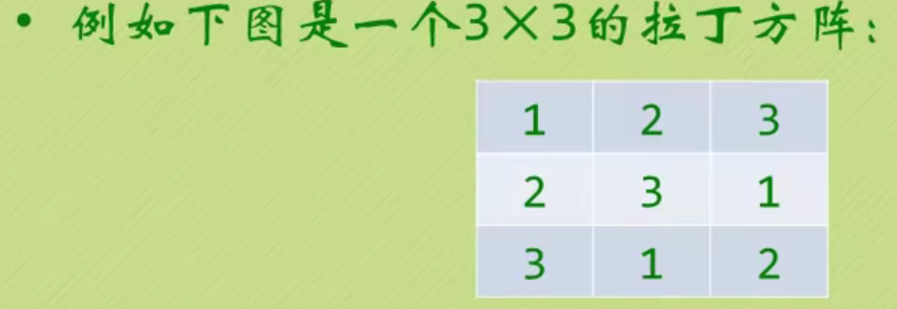

In fact, it is printed in the order of rings
The code is as follows. I put the licensing and Latin matrix in one file.
#include <iostream>
#include<stdio.h>
#include<stdlib.h>
using namespace std;
static int CardNumber=13;
typedef struct Node
{
int data;
struct Node * next;
}sqlist,*LinkList;
typedef struct Node *LinkList;//It means that what is defined by LinkList is a pointer
/**
* Generation of circular linked list
*/
LinkList CreatLinkList(int n)
{
LinkList head=NULL;
LinkList s ,r;
int i;
r=head;
for(int i=0;i<n;i++)
{
s=(LinkList) malloc(sizeof (sqlist));
s->data=0;//The default is 0
if(head==NULL)
head=s;
else
r->next=s;
r=s;
}
r->next=head;
return head;
}
/**
* Destruction work
*/
void DestoryList(LinkList *List)
{
LinkList ptr=*List;
LinkList buff[CardNumber];
int i=0;
while (i<CardNumber)
{
buff[i++]=ptr;
ptr=ptr->next;
}
for(i=0;i<CardNumber;i++)
{
free(buff[i]);
}
*List=0;
}
/**
* Licensing sequence calculation
* @return
*/
void Magician(LinkList head)
{
LinkList p;
int j;
int Countnumber=2;
p=head;
p->data=1;
while (1)
{
for(j=0;j<Countnumber;j++)
{
p=p->next;
if(p->data!=0)//If there is a card in this position, the next position
{
p->next;//p=p->next;??
j--;
}
}
if(p->data==0)
{
p->data=Countnumber;
Countnumber++;
if(Countnumber==14)
break;;
}
}
}
/**
* Licensing problem test
*/
void Magician_Problem()
{
LinkList p;
int i,n;
//This is the licensing solution
p=CreatLinkList(CardNumber);
Magician(p);
cout<<"In the following order:"<<endl;
for(i=0;i<CardNumber;i++)
{
cout<<"spade"<<p->data;
p=p->next;
}
cout<<endl;
cout<<endl;
//DestoryList(&p);
}
/**
* Latin matrix problem
* It is realized by circular linked list
* For example, for a 3x3 Latin matrix, the first row is output from the first node, the second row is output from the second node, the third row vong is output from the third node. Output 3 data per row.
* @return
*/
void LatinMatrix(LinkList head,int n)
{
LinkList p;
p=head;
int j,i=1;
for(j=0;j<n;j++,i++)
{
if(p->data==0)
{
p->data=i;
}
p=p->next;//point
}
p=head;
//output
/* debug See if the linked list is as we think
for(int k=0;k<n;k++)
{
cout<<p->data<<" ";
p=p->next;
}*/
int count=0;
for(int k=0;k<n;k++)
{
for(int l=0;l<n;l++)
{
cout<<p->data;
p=p->next;
}
p=head;
count++;
for(int m=0;m<count;m++)
{
p=p->next;
}
cout<<endl;
}
}
/**
* Latin matrix problem
* @return
*/
void LatinMatrix_Problem()
{
LinkList p;
int n;
cout<<"Please enter the dimension of Latin matrix:"<<endl;
cin>>n;
p=CreatLinkList(n);
LatinMatrix(p,n);
cout<<endl;
//DestoryList(&p);
}
int main() {
int choice=1;
while(choice)
{
cout<<"Please enter 1 to select a licensing question"<<endl;
cout<<"Please enter 2 to select the Latin matrix question"<<endl;
cout<<"Exit, please enter 0"<<endl;
cin>>choice;
switch (choice) {
case 1 :
Magician_Problem();
break;
case 2 :
LatinMatrix_Problem();
break;
case 0 :
exit(0);
break;
}
}
return 0;
}
Bidirectional linked list


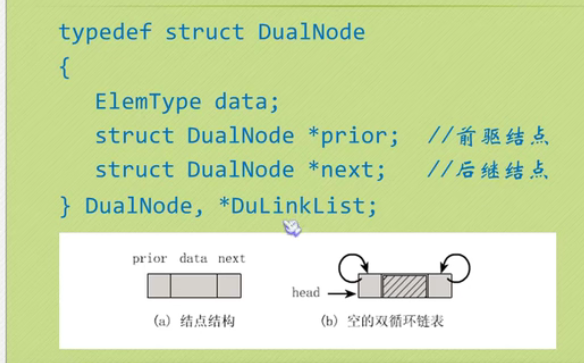
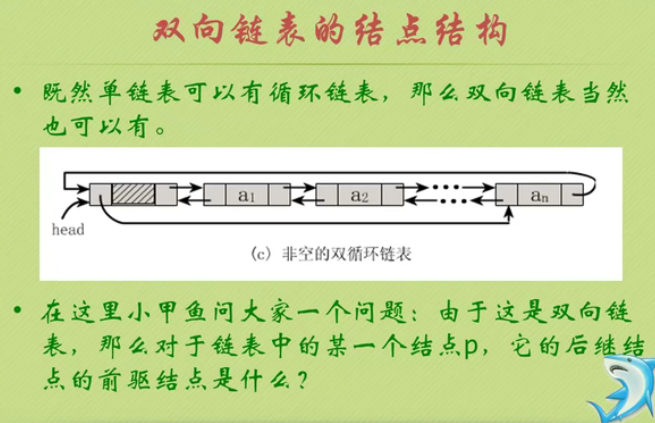
Insertion of bidirectional linked list
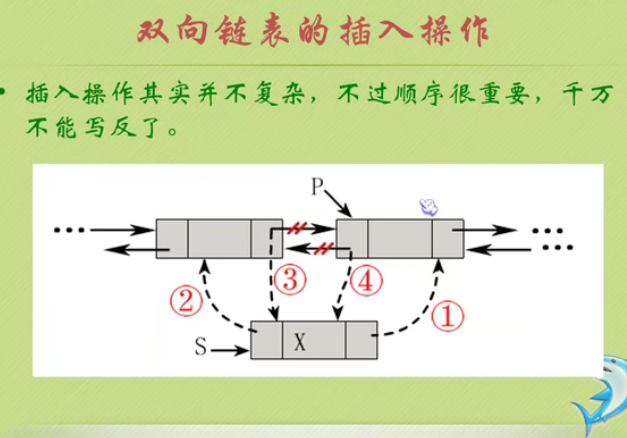

Deletion of bidirectional linked list
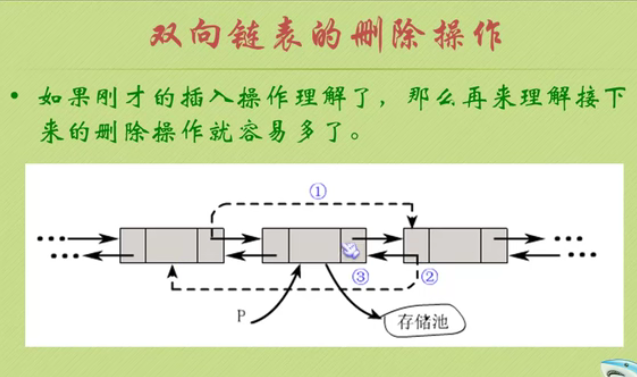


Practice of double line circular linked list

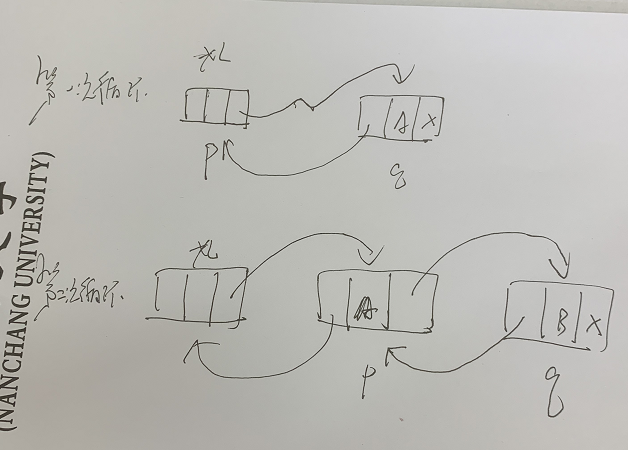
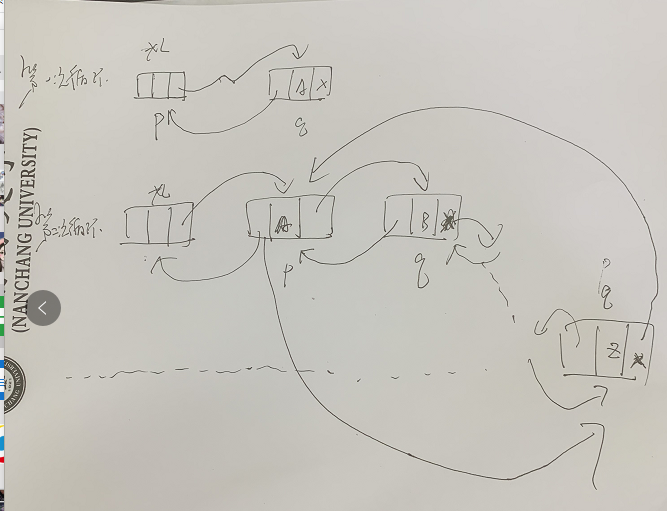
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
typedef char ElemType;
typedef int Status;
#define ERROR 0;
#define OK 1;
typedef struct DualNode
{
ElemType data;
struct DualNode *prior;//Precursor node
struct DualNode *next;//Rear drive node
}DualNode ,*DuLinkList;
/**
* Initialize linked list
* *L Represents a pointer, then L is the pointer to the pointer?
*/
Status InitList(DuLinkList *L)
{
DualNode*p,*q;
int i;
*L=(DuLinkList) malloc(sizeof (DualNode));
if(!(*L))
{
return ERROR;
}
(*L)->next=(*L)->prior=NULL;
p=(*L);//Now it's the head node. Don't assign it a value
for(i=0;i<26;i++)
{
q=(DuLinkList) malloc(sizeof (DualNode));
if(!q)
{
return ERROR;
}
q->data='A'+i;
q->prior=p;
q->next=p->next;//There's nothing here
p->next=q;
p=q;
}
p->next=(*L)->next;
(*L)->next->prior=p;
return OK;
}
void Caesar(DuLinkList *L,int i)
{
if(i>0)
{
do
{
(*L)=(*L)->next;
}while(--i);
}
if(i<0)//It's worth thinking about the source code. There's a problem with this one. I changed it
{
(*L)=(*L)->next;
do
{
(*L)=(*L)->prior;
}while(i++);
}
}
int main() {
DuLinkList L;
int i,n;
InitList(&L);//Pass in the address of pointer L, and the parameter of the function is * l, then * l is the pointer to the linked list inside the function
cout<<"please enter an integer n:"<<endl;
cin>>n;
cout<<endl;
Caesar(&L,n);
for( i=0;i<26;i++)
{
L=L->next;
cout<<L->data;
}
cout<<endl;
return 0;
}
Vingenre encryption – job

The code is as follows. I put Vigenere together with the problem of alphabet sorting.
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <vector>
using namespace std;
typedef char ElemType;
typedef int Status;
#define ERROR 0;
#define OK 1;
typedef struct DualNode
{
ElemType data;
struct DualNode *prior;//Precursor node
struct DualNode *next;//Rear drive node
}DualNode ,*DuLinkList;
/**
* Initialize linked list
* *L Represents a pointer, then L is the pointer to the pointer?
* Node containing header has no value
*/
Status InitList(DuLinkList *L)
{
DualNode*p,*q;
int i;
*L=(DuLinkList) malloc(sizeof (DualNode));
if(!(*L))
{
return ERROR;
}
(*L)->next=(*L)->prior=NULL;
p=(*L);//Now it's the head node. Don't assign it a value
for(i=0;i<26;i++)
{
q=(DuLinkList) malloc(sizeof (DualNode));
if(!q)
{
return ERROR;
}
q->data='A'+i;
q->prior=p;
q->next=p->next;//There's nothing here
p->next=q;
p=q;
}
p->next=(*L)->next;
(*L)->next->prior=p;
return OK;
}
/**
* Solution of alphabet problem
* @param L
* @param i
*/
void Caesar(DuLinkList *L,int i)
{
if(i>0)
{
do
{
(*L)=(*L)->next;
}while(--i);
}
if(i<0)
{
(*L)=(*L)->next;
do
{
(*L)=(*L)->prior;
}while(i++);
}
}
/**
* The alphabet is output at the specified position
* @return
*/
void alpha_cout()
{
DuLinkList L;
int i,n;
InitList(&L);//Pass in the address of pointer L, and the parameter of the function is * l, then * l is the pointer to the linked list inside the function
cout<<"please enter an integer n:"<<endl;
cin>>n;
cout<<endl;
Caesar(&L,n);
for( i=0;i<26;i++)
{
L=L->next;
cout<<L->data;
}
cout<<endl;
}
//Keys and ciphertext
struct mmWen
{
int mishi;//key
char miwen='0';//ciphertext
};
/**
* Vingenre Solution of encryption problem
* A random number will be generated for each letter (make this number in the range of 0-49)
* Then save the keys and inscriptions of each letter in the mmWen data structure corresponding to each letter
* @return
*/
void Vingenre()
{
vector<mmWen> mmWem_;//Store the ciphertext and key corresponding to A-Z
DuLinkList L,p;
InitList(&L);//Pass in the address of pointer L, and the parameter of the function is * l, then * l is the pointer to the linked list inside the function
//The text is as follows
//debug to see if the output is the 26 letters you want
cout<<"The plaintext and the corresponding key are as follows"<<endl;
for(int i=0;i<26;i++)
{
L=L->next;
cout<<L->data<<" ";
}
p=L->next;p Point to letter A Node of
cout<<endl;
srand((int)time(NULL));
for(int i = 0; i < 26;i++ )
{
int j= rand()%9;
cout <<j << " ";
mmWen t;
t.mishi=j;
mmWem_.push_back(t);//Save key
}
cout<<endl;
/* //debug Used to test whether the key is stored in the corresponding struct
for(auto a:mmWem_)
{
cout<<a.mishi<<" ";
}*/
//Put the ciphertext and key directly in the container
for(int i=0;i<26;i++)
{
//int m=(p->data)-'A';// Serial number corresponding to plaintext
int n=i+mmWem_[i].mishi;//Get the letter sequence number corresponding to the key
for(int j=0;j<n;j++)//Find the node corresponding to the ciphertext
{
p=p->next;
}
mmWem_[i].miwen=p->data;
p=L->next;//p points back to the letter A
}
for(auto a:mmWem_)
{
cout<<"Ciphertext:"<<a.miwen<<" "<<"Key:"<<a.mishi;
cout<<endl;
}
char c;
cout<<"Press 0 to exit!!!"<<endl;
cout<<"Enter plaintext:"<<endl;
while(1)
{
cin>>c;
if(c=='0')
{
break;
}
else
{
int m=c-'A';//Serial number corresponding to plaintext
for(int i=0;i<m;i++)//Location of plaintext found
{
p=p->next;
}
cout<<"Plaintext"<<p->data<<" "<<"Ciphertext:"<<mmWem_[m].miwen<<" "<<"Key:"<<mmWem_[m].mishi;
p=L->next;
}
cout<<endl;
cout<<endl;
cout<<"Press 0 to exit!!!"<<endl;
cout<<"Enter plaintext:"<<endl;
}
}
int main() {
int choice=1;
while(choice)
{
cout<<endl;
cout<<"Please enter 1 to select an alphabet output question"<<endl;
cout<<"choice Vingenre Encryption problem, please enter 2"<<endl;
cout<<"Exit, please enter 0"<<endl;
cin>>choice;
switch (choice) {
case 1 :
alpha_cout();
break;
case 2 :
Vingenre();
break;
case 0 :
exit(0);
break;
}
}
return 0;
}
Stack and queue

Definition of stack

Press push three times
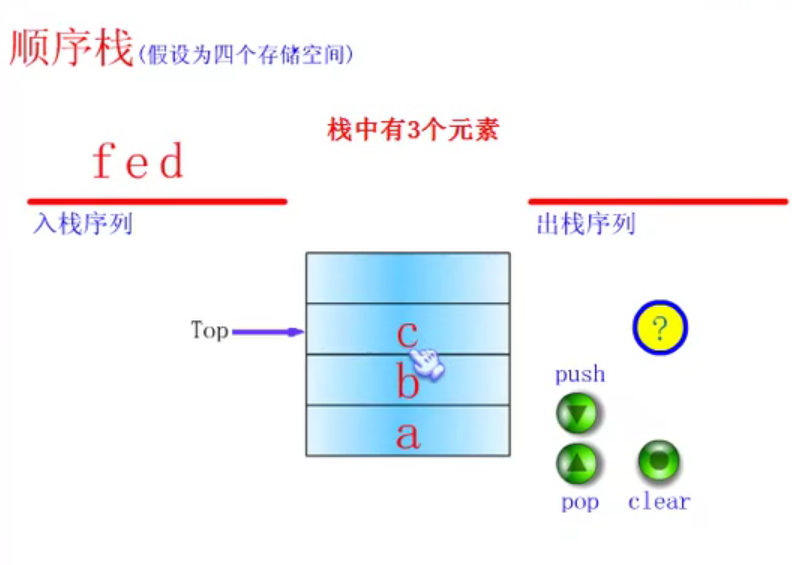
Click pop
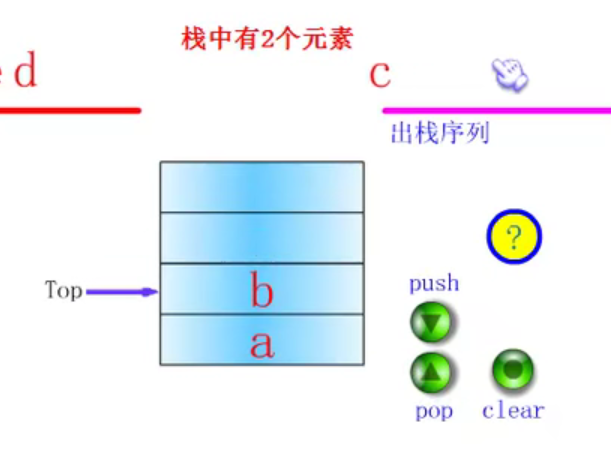
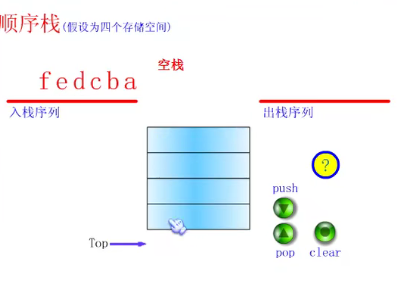
Sequential storage structure of stack

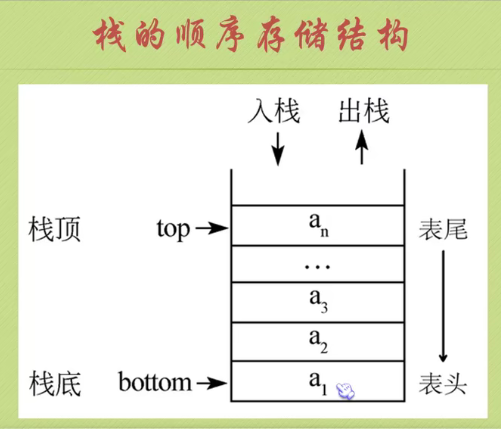


Stack operation


Out of stack operation

There is no data at the top of the stack. It is ready to store data.




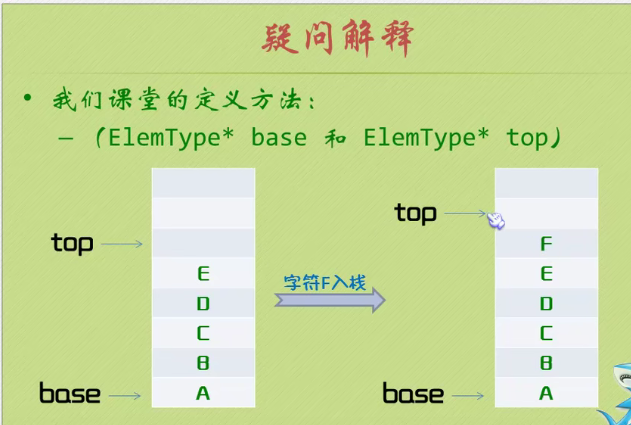


Empty stack

Destroy stack



example


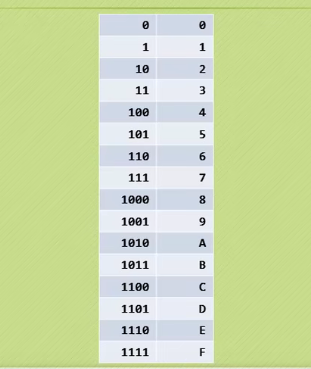

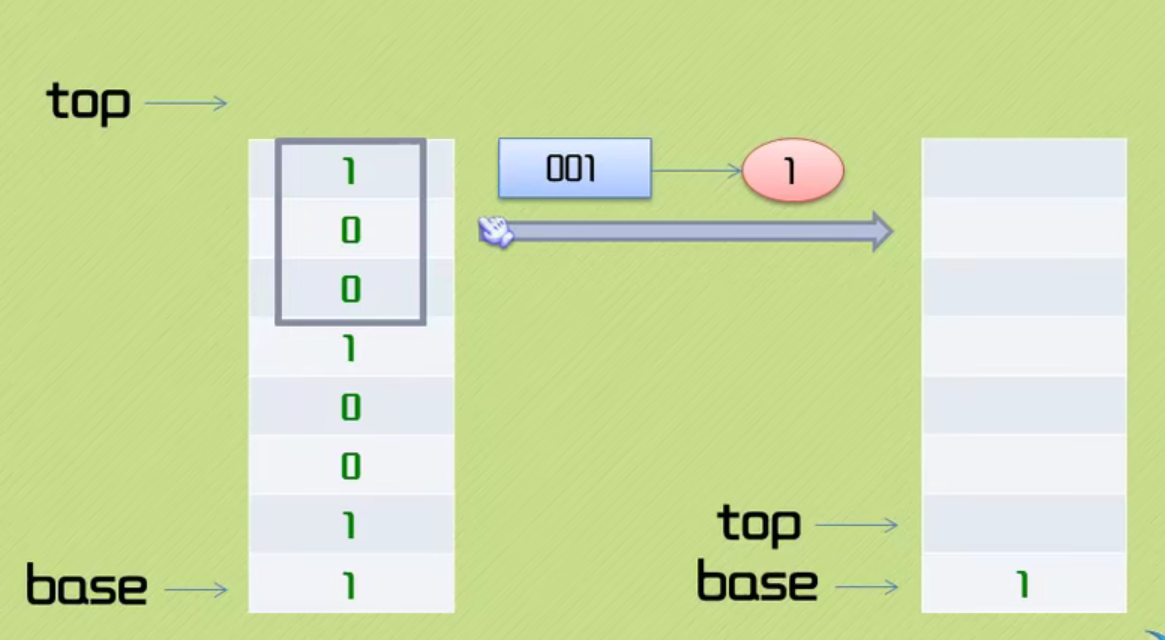
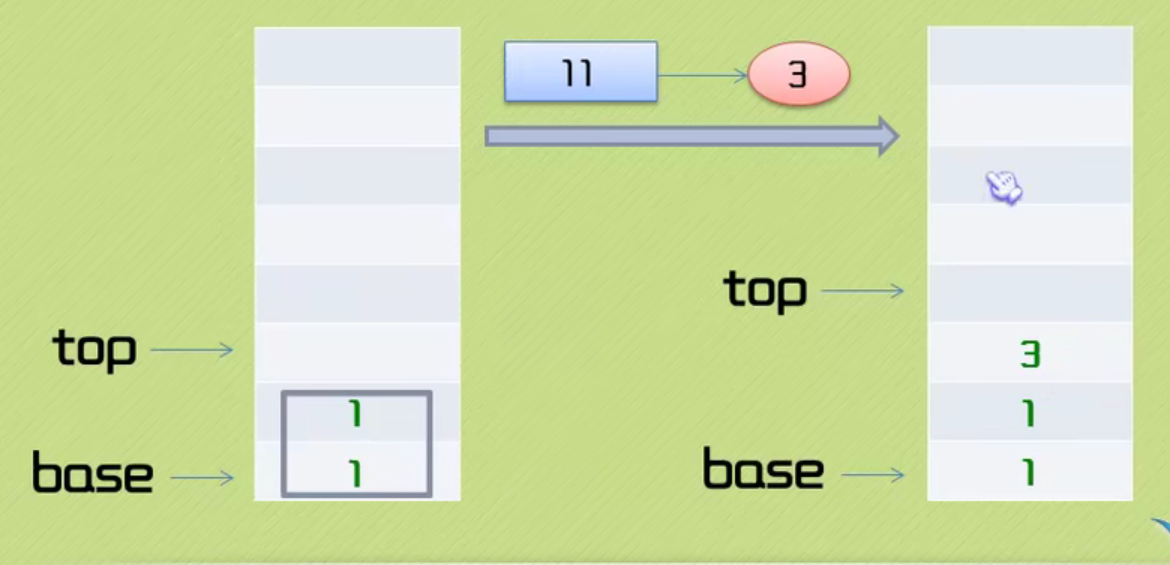
The code is as follows:
#include <iostream>
#include <math.h>
using namespace std;
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
typedef char ElemType;
typedef struct {
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
/**
* Create a stack
* @param s
*/
void initStack(sqStack *s)
{
s->base=(ElemType *) malloc(STACK_INIT_SIZE*sizeof (ElemType));
if(!s->base)
{
exit(0);
}
s->top=s->base;
s->stackSize=STACK_INIT_SIZE;
}
/**
* Push
* @return
*/
void Push(sqStack *s,ElemType e)
{
//If the stack is full, expand the space
if(s->top-s->base>=s->stackSize)
{
s->base=(ElemType *) realloc(s->base,(s->stackSize+STACKINCREMENT)*sizeof (ElemType));//realloc is to create a space on the right and copy it to the left
if(!s->base)
{
exit(0);
}
s->top= s->base+s->stackSize;//Position of stack top
s->stackSize=s->stackSize+STACKINCREMENT;//Reset stack capacity
}
*(s->top)=e;
s->top++;
}
/**
* Out of stack
* @return
*/
void pop(sqStack *s,ElemType *e)
{
if(s->top==s->base)
{
return ;
}
*e=*--(s->top);//Because top shows off that it does not store data, it is used to prepare to store the next data
}
/**
* Stack size
*/
int StackLen(sqStack s)
{
return (s.top-s.base);
}
/**
* empty
* @return
*/
void ClearStack(sqStack *s)
{
s->top=s->base;
}
/**
* Destroy stack
* @return
*/
void DestroyStack(sqStack *s)
{
int i,len;
len=s->stackSize;
for(i=0;i<len;i++)
{
free(s->base);
s->base++;
}
s->base=s->top=NULL;
s->stackSize=0;
}
/**
* Binary conversion decimal
* @return
*/
void TwoToTen()
{
ElemType c;
sqStack s;
initStack(&s);
int len ,i,sum=0;
cout<<"Please enter binary number#The symbol indicates the end! "<<endl;
cin>>c;
while(c!='#'/ / don't use' / n 'because the Assic of / n is 10. If you enter one, you need to press the newline character, and the newline will also be pushed as input
{
Push(&s,c);
cin>>c;
}
getchar();//After all are accepted, the keyboard will accept an Assic of '/ n' / n, which is 10. Therefore, to filter out this 10, use getchar() to get '/ n';
len= StackLen(s);
cout<<"Current capacity of stack:"<<len<<endl;
for(i=0;i<len;i++)
{
pop(&s,&c);
sum=sum+(c-48)*pow(2,i);
}
cout<<"Convert to decimal: "<<sum<<endl;
}
/**
* Binary conversion octal only needs to build another stack and calculate octal with a three cycle
* @return
*/
int main() {
TwoToTen();
return 0;
}
Chain storage structure of stack

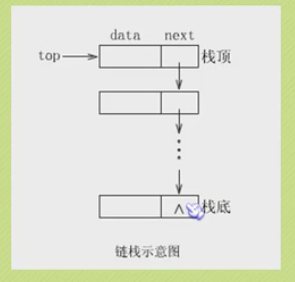

Stacking of chain stack
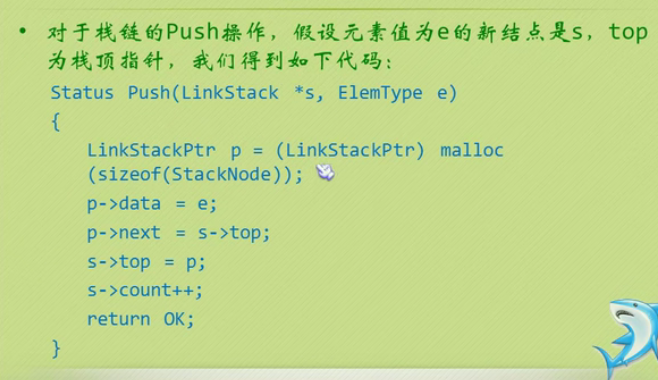
Out of chain stack

practice



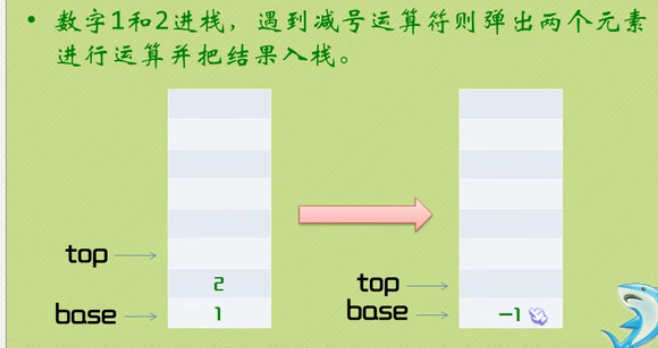
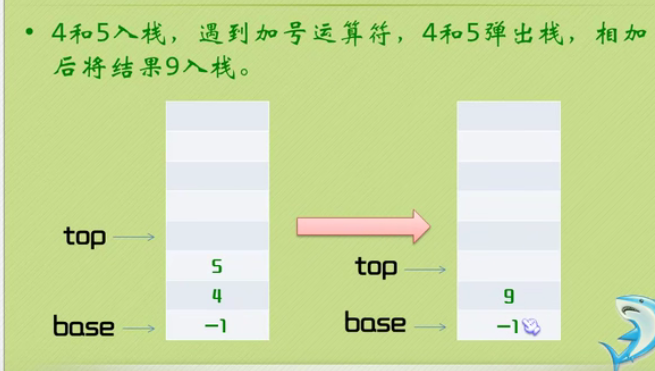
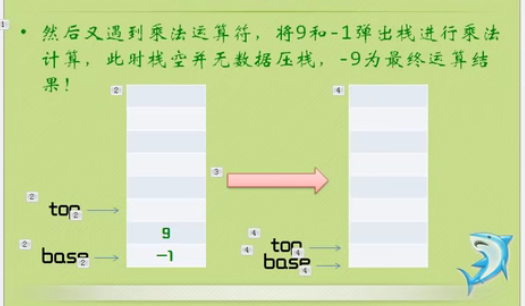
Inverse Polish calculator


At present, there is a problem with the code running on your own computer. It is implemented the same as the code of little turtle, but I don't know what went wrong.
Found the problem. It's a problem with input statements. You can't use cin, because cin automatically ignores spaces. Fuck!
Reference blog
#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <ctype.h>
using namespace std;
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef float ElemType;
typedef struct {
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
/**
* Create a stack
* @param s
*/
void initStack(sqStack *s)
{
s->base=(ElemType *) malloc(STACK_INIT_SIZE*sizeof (ElemType));
if(!s->base)
{
exit(0);
}
s->top=s->base;
s->stackSize=STACK_INIT_SIZE;
}
/**
* Push
* @return
*/
void Push(sqStack *s,ElemType e)
{
//If the stack is full, expand the space
if(s->top-s->base>=s->stackSize)
{
s->base=(ElemType *) realloc(s->base,(s->stackSize+STACKINCREMENT)*sizeof (ElemType));//realloc is to create a space on the right and copy it to the left
if(!s->base)
{
exit(0);
}
s->top= s->base+s->stackSize;//Position of stack top
s->stackSize=s->stackSize+STACKINCREMENT;//Reset stack capacity
}
*(s->top)=e;
s->top++;
}
/**
* Out of stack
* @return
*/
void Pop(sqStack *s,ElemType *e)
{
if(s->top==s->base)
{
return ;
}
*e=* --(s->top);//Because top does not store data, it is used to prepare to store the next data
}
/**
* Stack size
*/
int StackLen(sqStack s)
{
return (s.top-s.base);
}
/**
* empty
* @return
*/
void ClearStack(sqStack *s)
{
s->top=s->base;
}
/**
* Destroy stack
* @return
*/
void DestroyStack(sqStack *s)
{
int i,len;
len=s->stackSize;
for(i=0;i<len;i++)
{
free(s->base);
s->base++;
}
s->base=s->top=NULL;
s->stackSize=0;
}
/**
* Polish calculator
*/
int main() {
sqStack s;
char c;
int i=0;
float d,e;
char str[MAXBUFFER];
initStack(&s);
cout<<"Please press the inverse Polish expression to enter data with calculation. The data and operators are separated by spaces to#As an end flag: "< < endl;
cin>>c;
while(c != '#')
{
while(isdigit(c) || c=='.')//Used to filter numbers
{
str[i++]=c;
str[i]='\0';
if(i>=10)
{
cout<<"Error: the single data entered is too large!"<<endl;
return -1;
}
cin>>c;
if(c==' ')
{
d=atof(str);//Convert to double
Push(&s,d);
i=0;
break;
}
}
switch(c)
{
case '+':
Pop(&s,&e);//Note that the data in the Stack here is double
Pop(&s,&d);
Push(&s,d+e);
break;
case '-':
Pop(&s,&e);//Note that the data in the Stack here is double
Pop(&s,&d);
Push(&s,d-e);
break;
case '*':
Pop(&s,&e);//Note that the data in the Stack here is double
Pop(&s,&d);
Push(&s,d*e);
break;
case '/':
Pop(&s,&e);//Note that the data in the Stack here is double
Pop(&s,&d);
if(e!=0)
{
Push(&s,d/e);
}
else
{
cout<<"Error: divisor is zero!"<<endl;
return -1;
}
break;
}
cin>>c;
}
Pop(&s,&d);
cout<<"Final calculation results:"<<d<<endl;
return 0;
}
Here is the correct code:
#include <stdio.h>
#include <ctype.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef double ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
void Push(sqStack *s, ElemType e)
{
// Stack full, additional space, fish oil must understand!
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e; // Store data
s->top++;
}
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
return;
*e = *--(s->top); // Pop up the stack top element and modify the stack top pointer
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
sqStack s;
char c;
double d, e;
char str[MAXBUFFER];
int i = 0;
InitStack( &s );
printf("Please enter the data to be calculated according to the inverse Polish expression. The data and operator are separated by spaces to#As an end flag: \ n "");
scanf("%c", &c);
//cin>>c ;
while( c != '#' )
{
while( isdigit(c) || c=='.' ) // Used to filter numbers
{
str[i++] = c;
str[i] = '\0';
if( i >= 10 )
{
printf("Error: the single data entered is too large!\n");
return -1;
}
scanf("%c", &c);
//cin>>c ;
if( c == ' ' )
{
d = atof(str);
Push(&s, d);
i = 0;
break;
}
}
switch( c )
{
case '+':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d+e);
break;
case '-':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d-e);
break;
case '*':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d*e);
break;
case '/':
Pop(&s, &e);
Pop(&s, &d);
if( e != 0 )
{
Push(&s, d/e);
}
else
{
printf("\n Error: divisor is zero!\n");
return -1;
}
break;
}
scanf("%c", &c);
//cin>>c;
}
Pop(&s, &d);
printf("\n The final calculation result is:%f\n", d);
return 0;
}
// 5 - (6 + 7) * 8 + 9 / 4
// 5 - 13 * 8 + 9 / 4
// 5 - 104 + 2.25
// -99 + 2.25
// 5 6 7 + 8 * - 9 4 / +
Infix expression becomes suffix expression

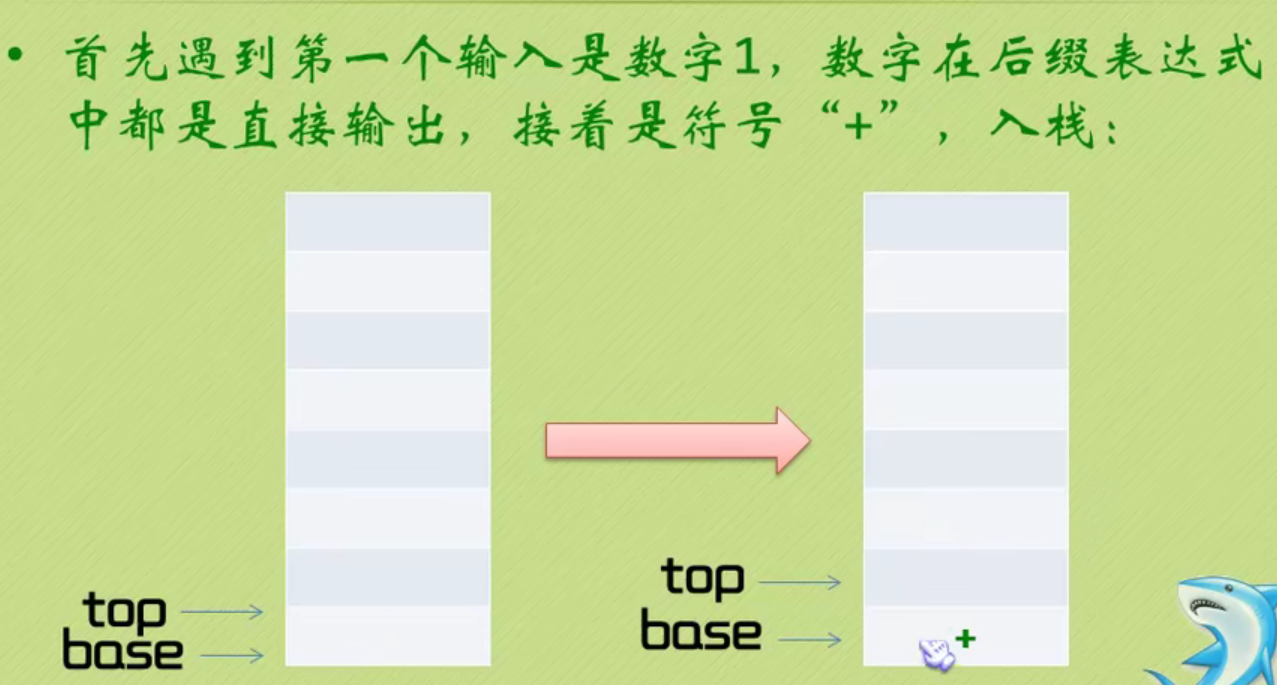
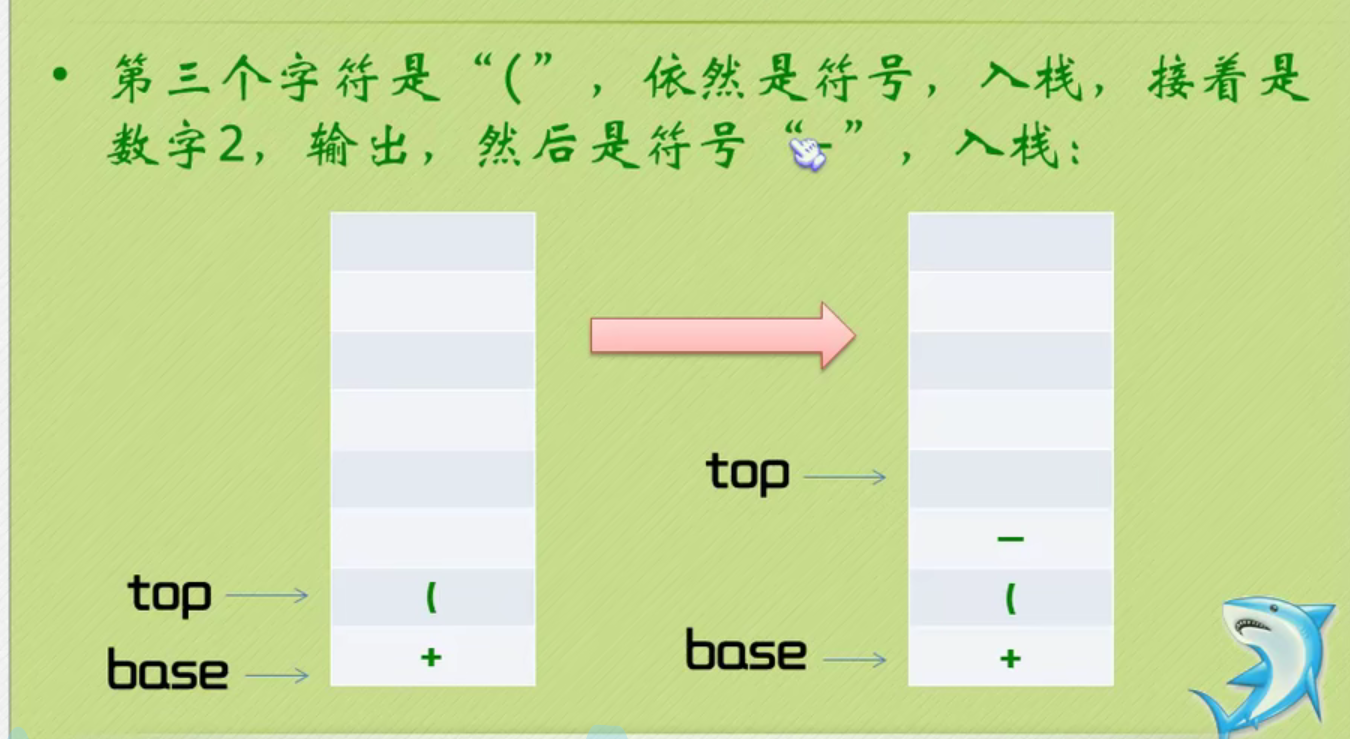
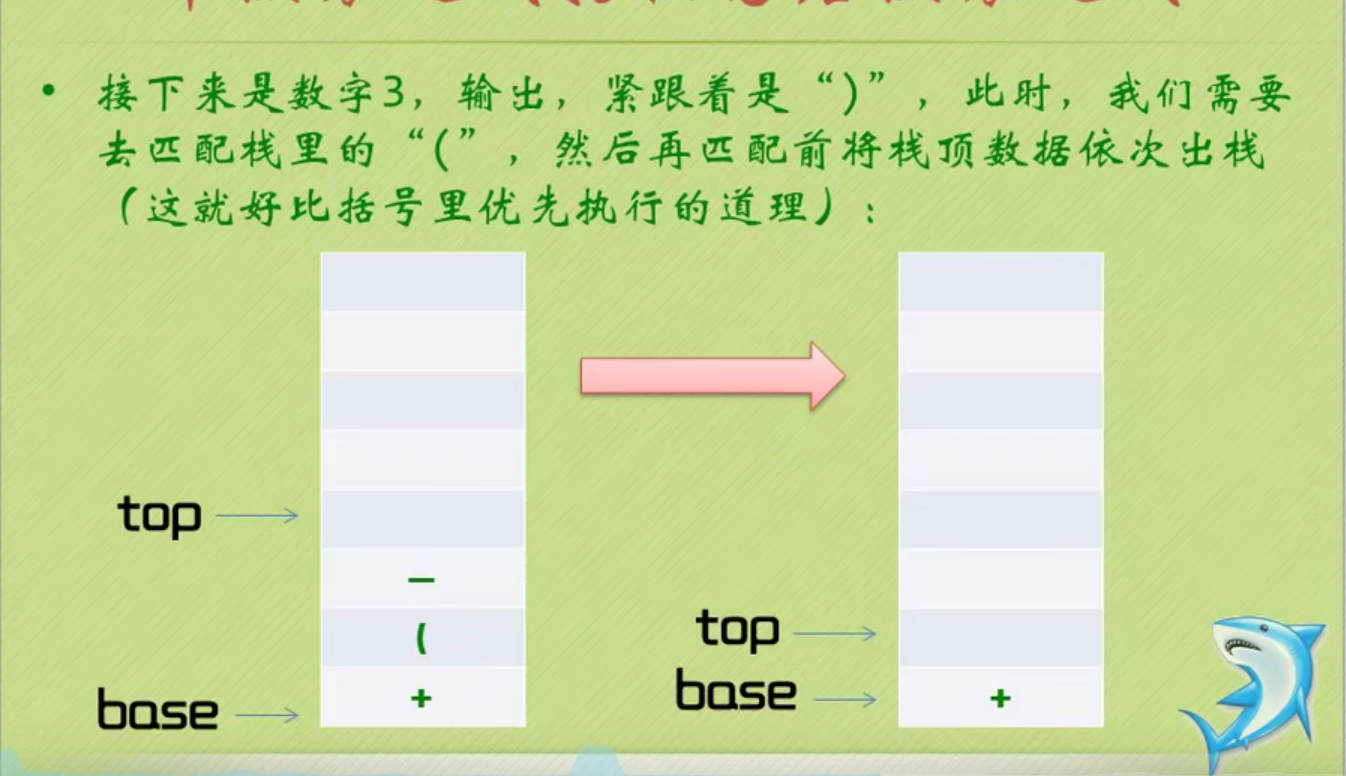
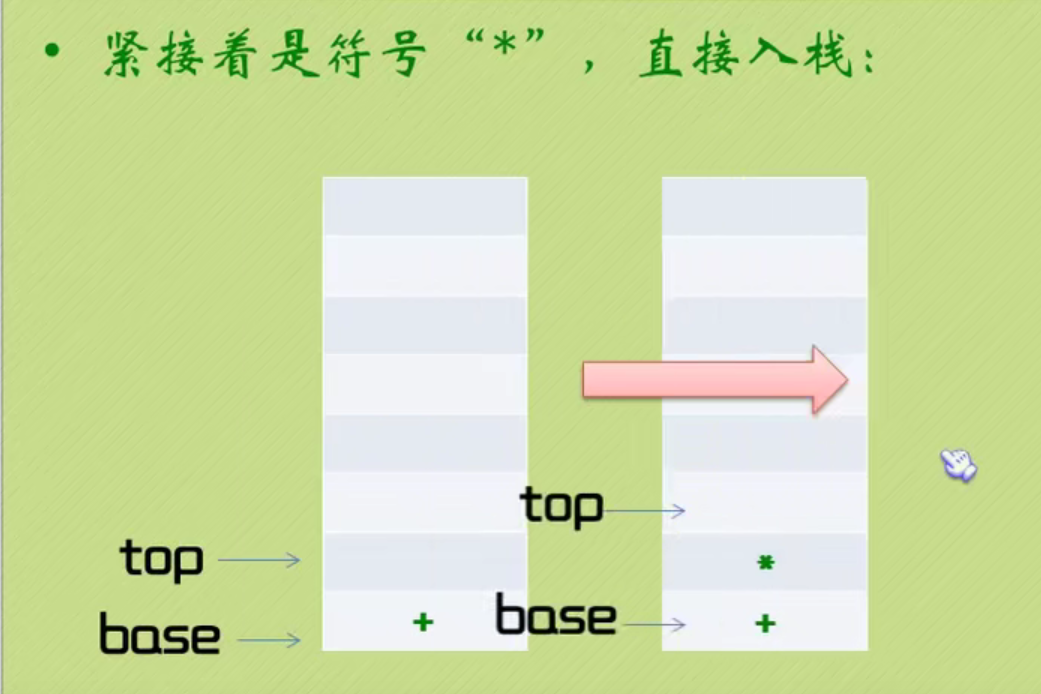

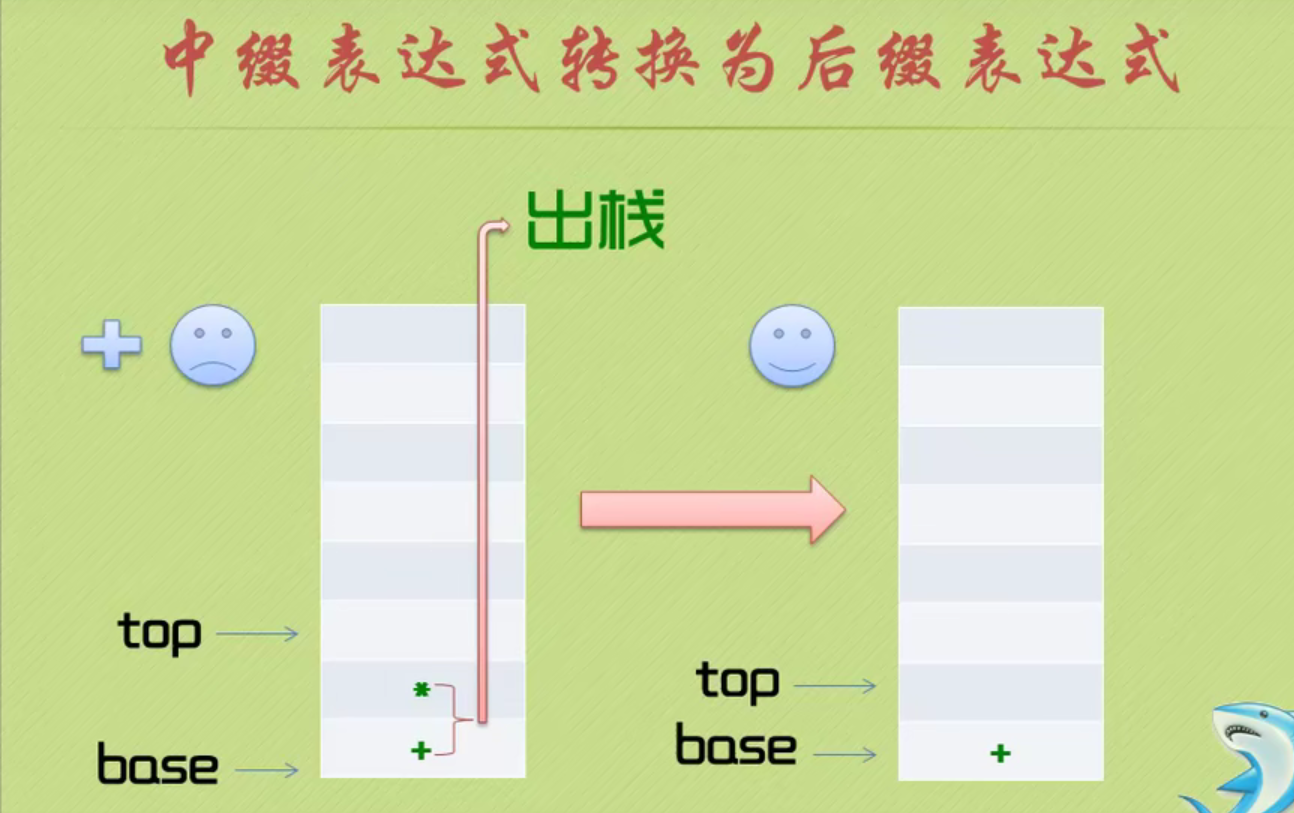
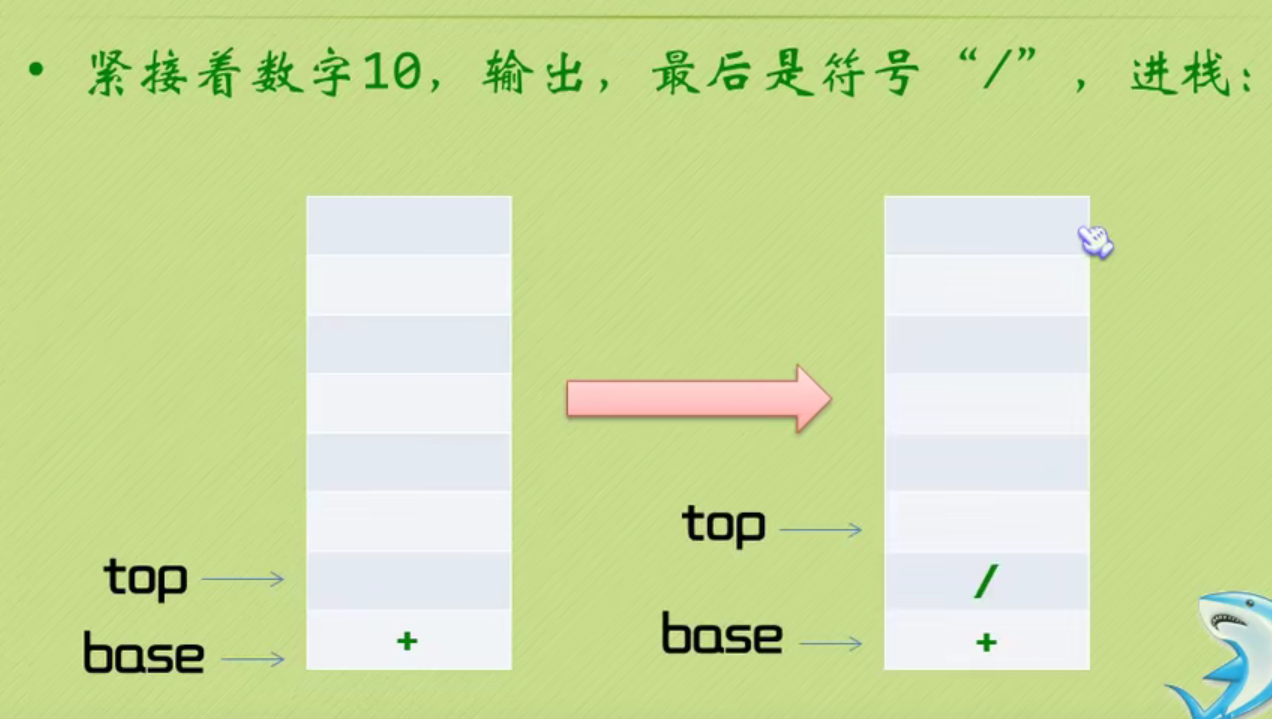

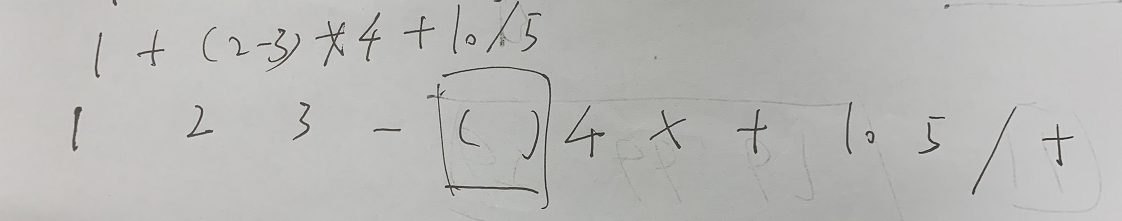

The complete code of infix expression to suffix expression + inverse Polish calculator is as follows:
#include <stdio.h>
#include <ctype.h>
#include <stdlib.h>
#include <iostream>
#include <string>
using namespace std;
/**
* Convert infix expression to suffix expression
*/
namespace mToL
{
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef char ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
void Push(sqStack *s, ElemType e)
{
// Stack full, additional space, fish oil must understand!
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e; // Store data
s->top++;
}
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
return;
*e = *--(s->top); // Pop up the stack top element and modify the stack top pointer
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
/**
* Convert infix expression to suffix expression
*/
string mToL_test()
{
//Convert infix expression to suffix expression
sqStack s;
InitStack( &s );
string str;
printf("Please enter infix expression to#As an end flag: ";
char c;
char e;
scanf("%c",&c);
while(c!='#')
{
while(isdigit(c) )
{
printf("%c", c);
str+=c;
scanf("%c", &c);
if(!isdigit(c) )//
{
printf(" ");
str+=' ';
}
}
if(')'==c)
{
Pop(&s,&e);//
while('('!=e)
{
printf("%c ", e);//The output character is followed by a space
str+=e;
str+=' ';
Pop(&s,&e);//
}
}
else if('+'==c||'-'==c)
{
if(!StackLen(s))//If stack is empty
{
Push(&s,c);
}
else
{
do
{
Pop(&s,&e);
if('('== e)//First judge whether there is an open parenthesis. If so, it means that c must be included in the parenthesis. Therefore, the left parenthesis should be placed in it until the right parenthesis is is used to match the operator in the pop-up parenthesis
{
Push(&s,e);//
}
else//If it is not the left bracket, it will pop up directly, such as 9 + 3 + (1 + 3) --- 9 3 - 1 3+
{
printf("%c ", e);//The output character is followed by a space
str+=e;
str+=' ';
}
}
while(StackLen(s) && '('!=e);//
Push(&s,c);
}
}
else if('*'==c|| '/'==c ||'('==c)
{
Push(&s,c);
}
else if( '#'== c )
{
break;
}
else
{
cout<<"Input format error!"<<endl;
//return -1;
}
scanf("%c",&c);
}
while( StackLen(s) )
{
Pop(&s, &e);
printf("%c ", e);
str+=e;
str+=' ';
//printf("%c ", e);
}
return str+'#';
}
}
/**
* Inverse Polish calculator
*/
namespace PolanCaulatuer
{
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef double ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
void Push(sqStack *s, ElemType e)
{
// Stack full, additional space, fish oil must understand!
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e; // Store data
s->top++;
}
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
return;
*e = *--(s->top); // Pop up the stack top element and modify the stack top pointer
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
/**
* Polish inverse calculator
*/
void PolanCaulauter(string strl)
{
sqStack s;
char c;
double d, e;
char str[MAXBUFFER];
int i = 0;
int j = 0;
InitStack( &s );
//printf("please input the data to be calculated according to the inverse Polish expression, and separate the data from the operator with a space to # serve as the end flag: \ n");
//scanf("%c", &c);
//cin>>c ;
c=strl[0];
cout<<"size: "<<strl.size()<<endl;
while( c != '#')
{
while( isdigit(c) || c=='.' ) // Used to filter numbers
{
str[i++] = c;
str[i] = '\0';
if( i >= 10 )
{
printf("Error: the single data entered is too large!\n");
//return -1;
}
c=strl[++j];
//scanf("%c", &c);
//cin>>c ;
if( c == ' ' )
{
d = atof(str);
Push(&s, d);
i = 0;
break;
}
}
switch( c )
{
case '+':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d+e);
break;
case '-':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d-e);
break;
case '*':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d*e);
break;
case '/':
Pop(&s, &e);
Pop(&s, &d);
if( e != 0 )
{
Push(&s, d/e);
}
else
{
printf("\n Error: divisor is zero!\n");
//return -1;
}
break;
default:
break;
}
c=strl[++j];
//scanf("%c", &c);
//cin>>c;
}
Pop(&s, &d);
printf("\n The final calculation result is:%f\n", d);
// 5 - (6 + 7) * 8 + 9 / 4
// 5 - 13 * 8 + 9 / 4
// 5 - 104 + 2.25
// -99 + 2.25
// 5 6 7 + 8 * - 9 4 / +
}
}
int main()
{
string s;
s=mToL::mToL_test();
cout<<endl;
cout<<s<<endl;
PolanCaulatuer::PolanCaulauter(s);
return 0;
}
Queue queue
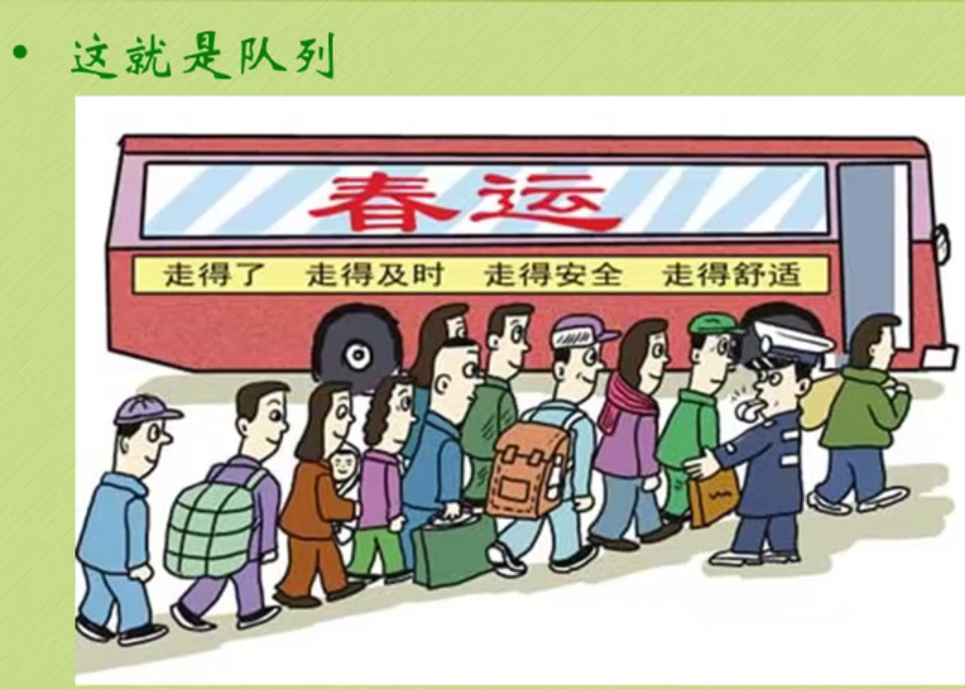



Create a queue

Queued operation
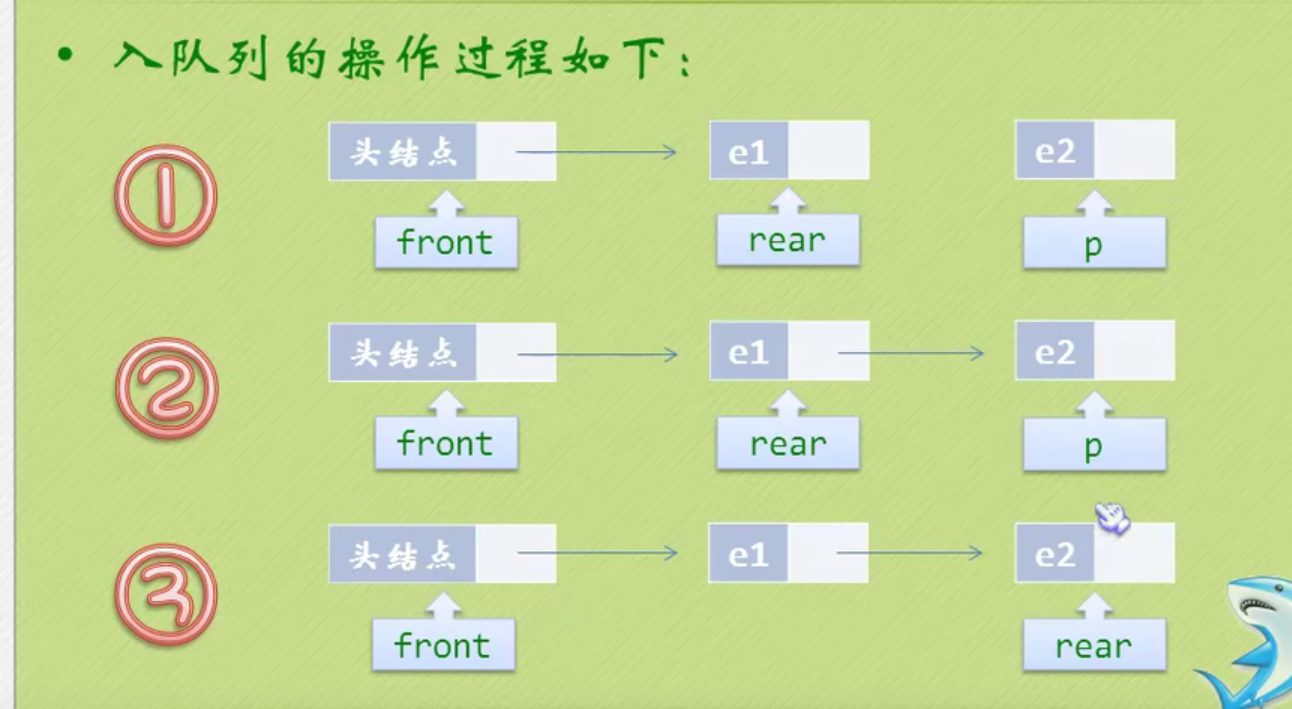
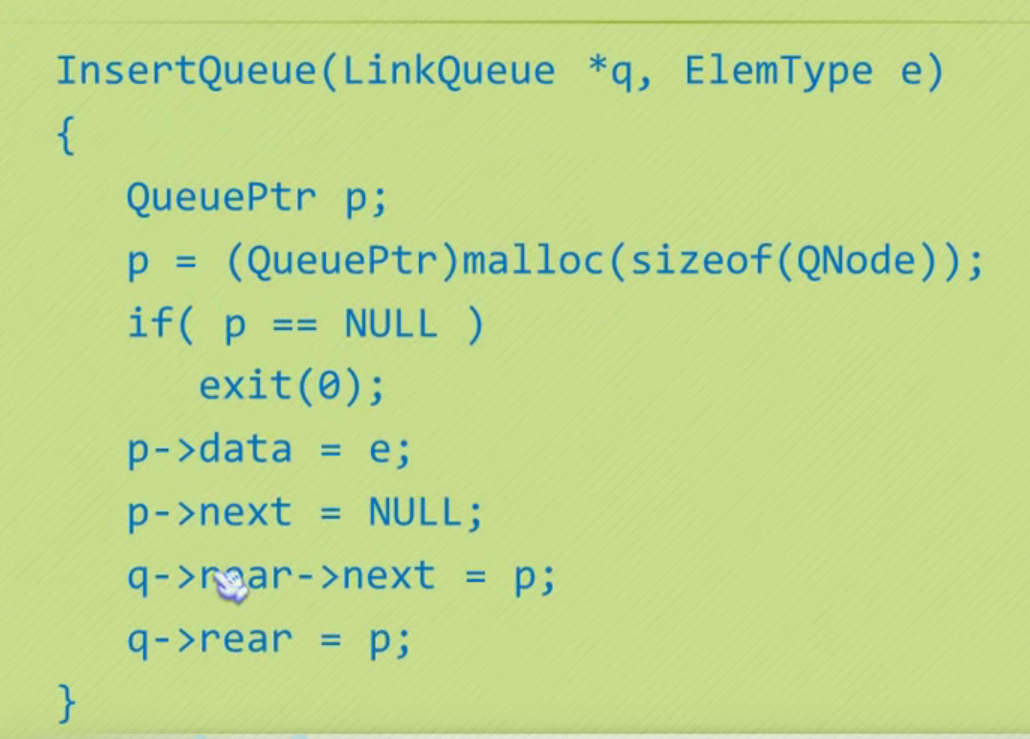
Out of queue operation
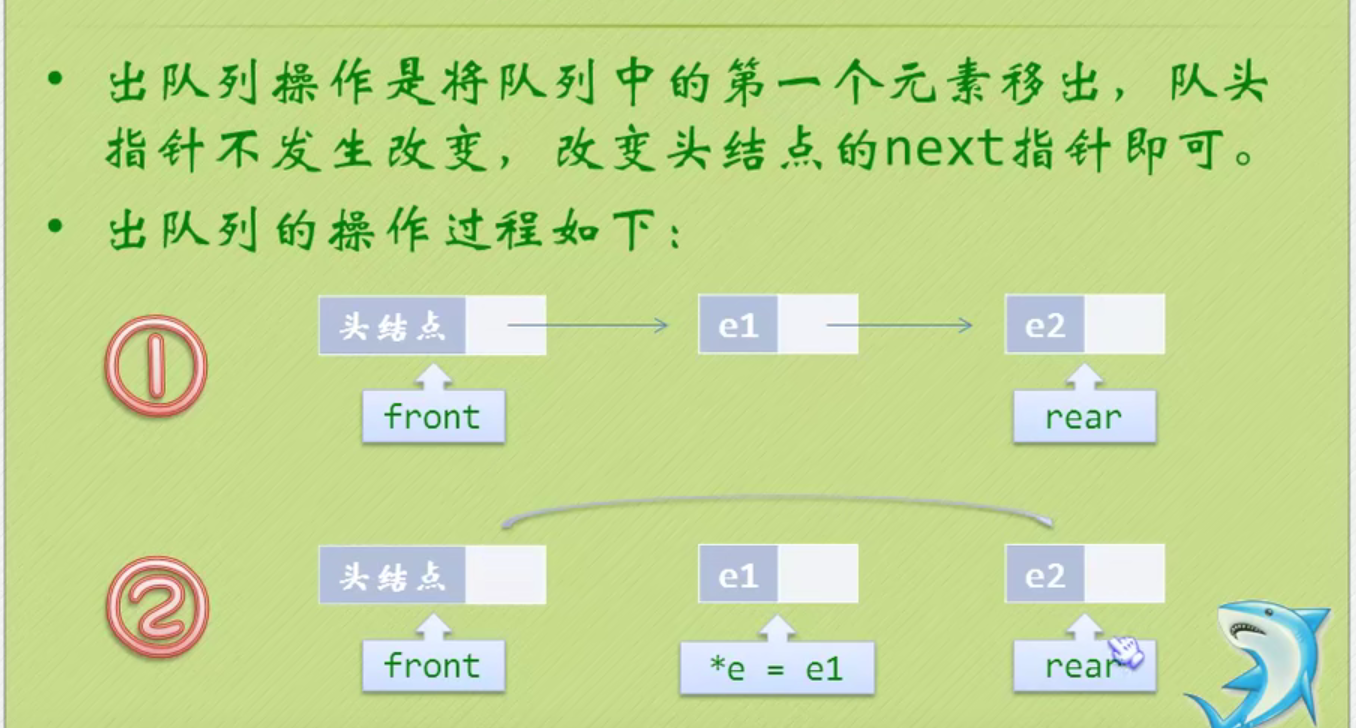
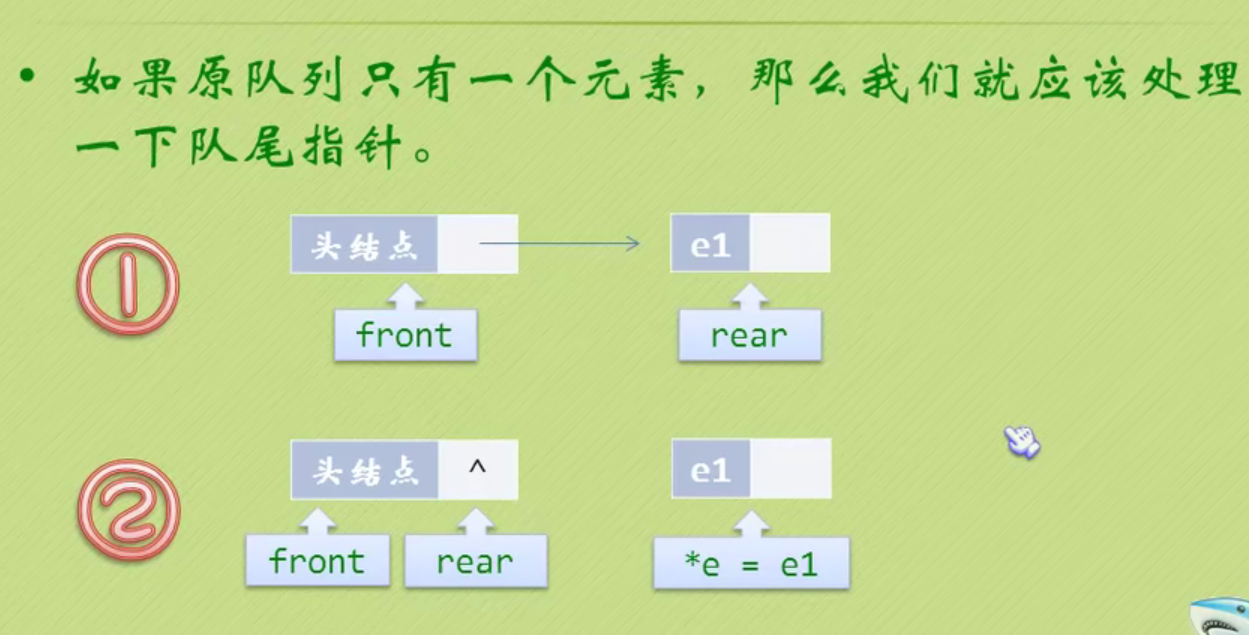

Destroy a queue

#include <iostream>
using namespace std;
typedef char ElemType;
typedef struct QNode
{
ElemType data;
struct QNode *next;
}QNode,*QueuePtr ;
typedef struct {
QueuePtr front,rear;//Point to the header and tail nodes, and the header does not store data
}LinkQueue;
/**
* Initialize queue
* @param q
*/
void initQueue(LinkQueue *q)
{
q->front=q->rear=(QueuePtr) malloc(sizeof (QNode));
if(!q->front)
{
exit(0);
q->front->next=NULL;
}
}
/**
* Enter queue
* @param q
* @param e
*/
void InsertQueue(LinkQueue *q,ElemType e)
{
QueuePtr p;
p=(QueuePtr) malloc(sizeof (QNode));
p->data=e;
p->next=NULL;
q->rear->next=p;
q->rear=p;
}
/**
* Out of queue
* @param q
* @param e
*/
void DeleteQueue(LinkQueue *q,ElemType *e)
{
QueuePtr p;
if(q->front==q->rear)//Empty queue
return;
p=q->front->next;
*e=p->data;
q->front->next=p->next;
if(q->rear==p)//There is only one element
{
q->rear=q->front;
}
free(p);
}
/**
* Destroy queue
* @param q
*/
void DestoryQueue(LinkQueue *q)
{
while(q->front)
{
q->rear=q->front->next;//Point to the next node after each node to be destroyed
free(q->front);
q->front=q->rear;//Move the first node back
}
}
int main() {
ElemType c;
LinkQueue q;
initQueue(&q);
cout<<"Please enter a string to#No. end input. "<<endl;
scanf("%c", &c);
while('#'!=c)
{
InsertQueue( &q, c );
scanf("%c", &c);
}
cout<<"Elements in the print queue:"<<endl;
while(q.front!=q.rear)
{
DeleteQueue( &q, &c );
cout<<c;
}
cout<<endl;
return 0;
}
Sequential storage of queues

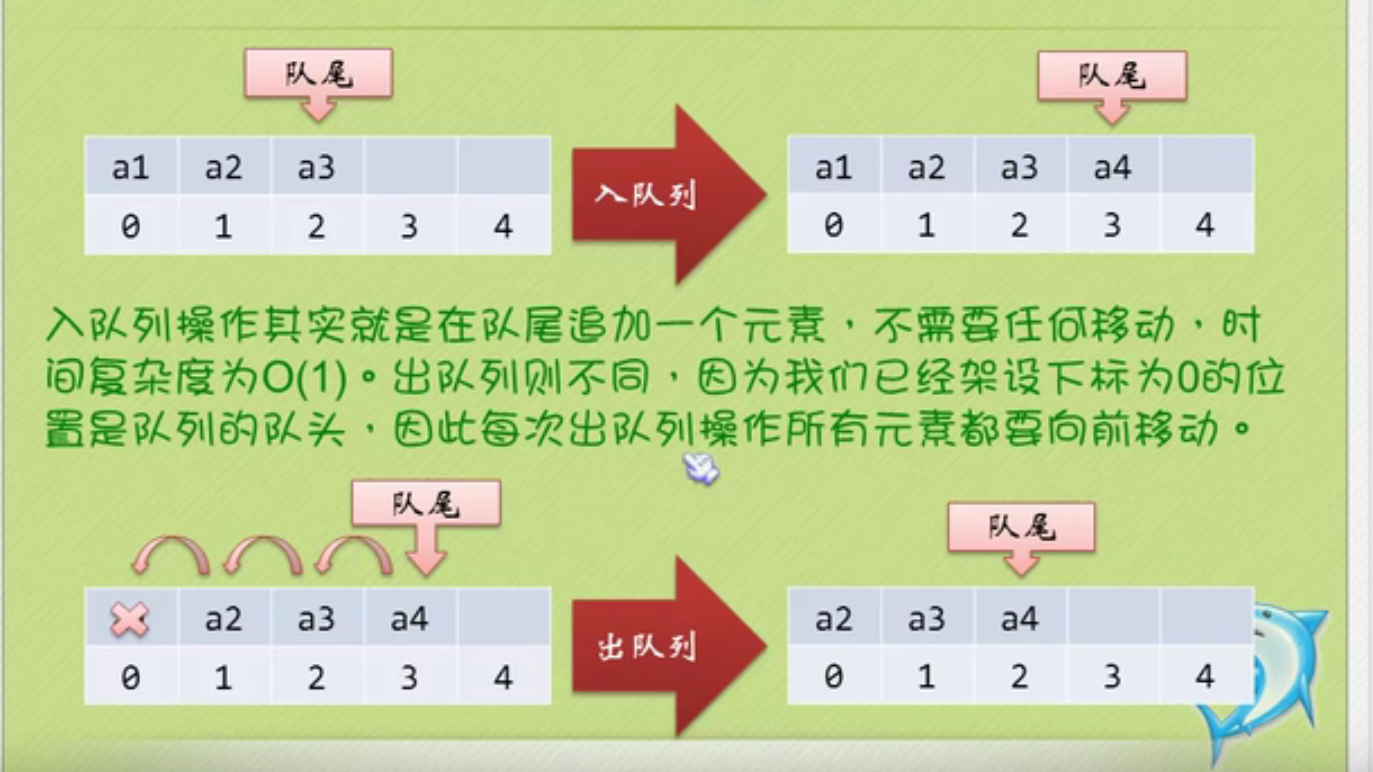

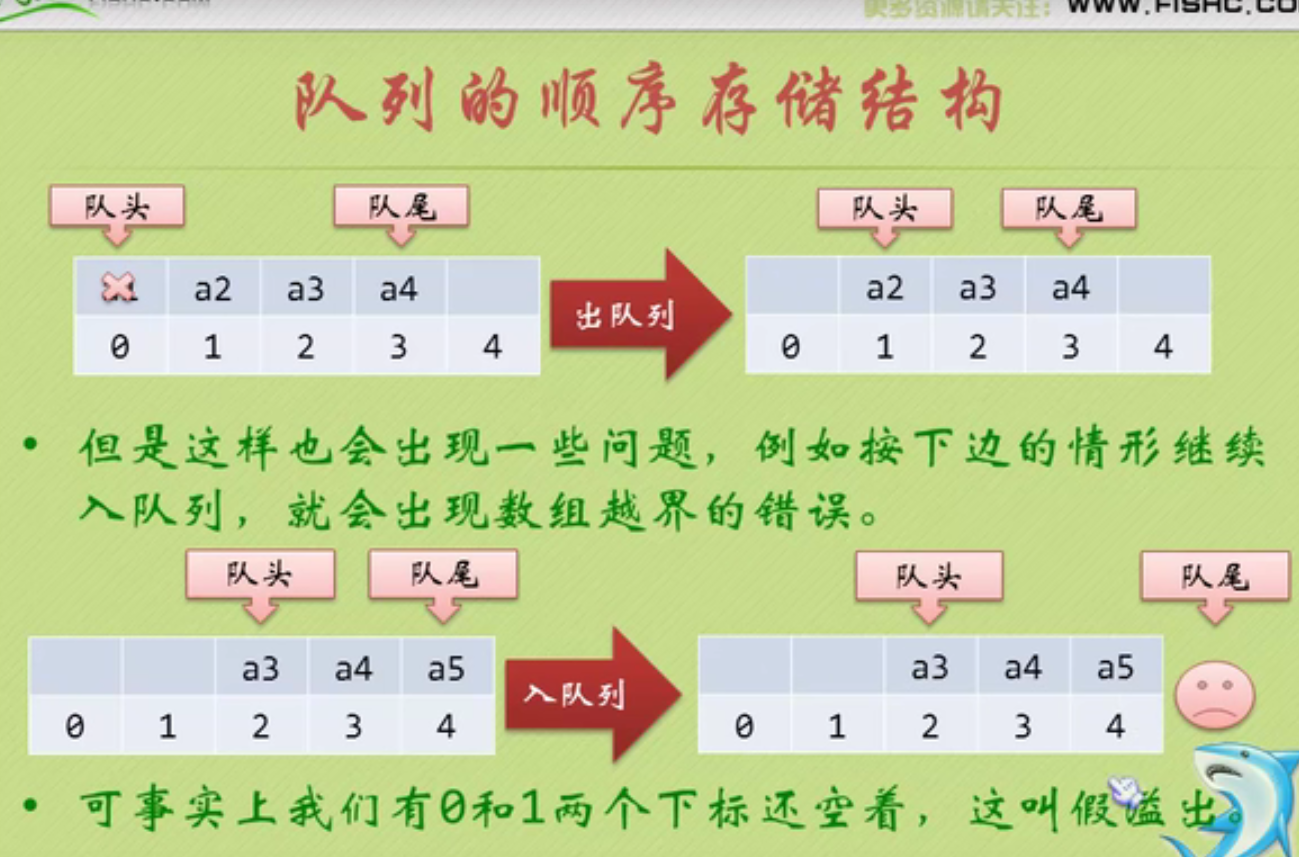
Circular queue

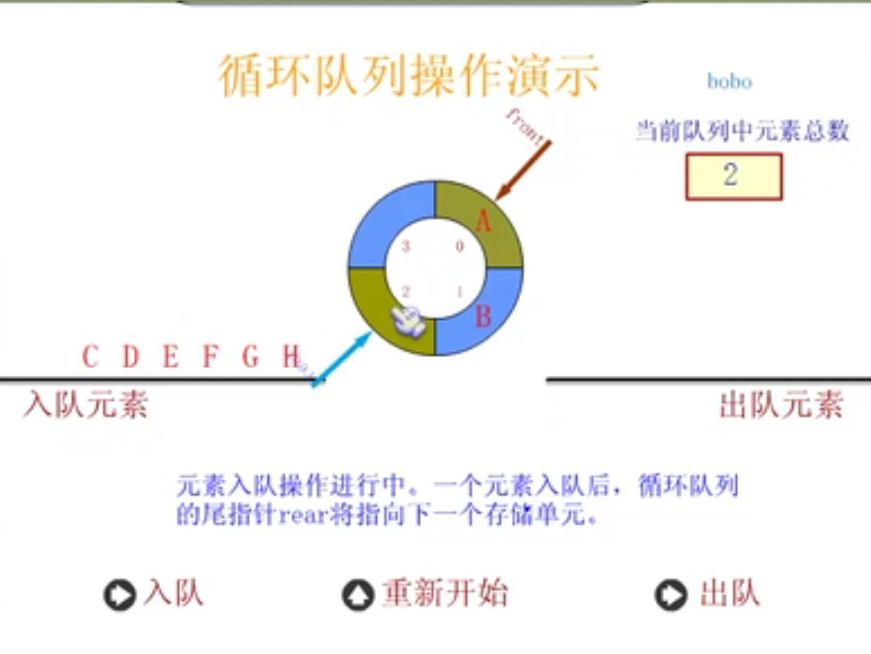
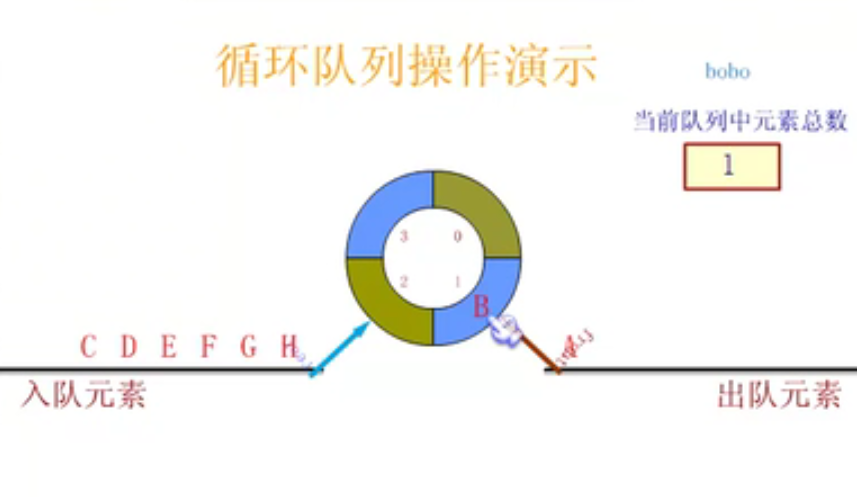
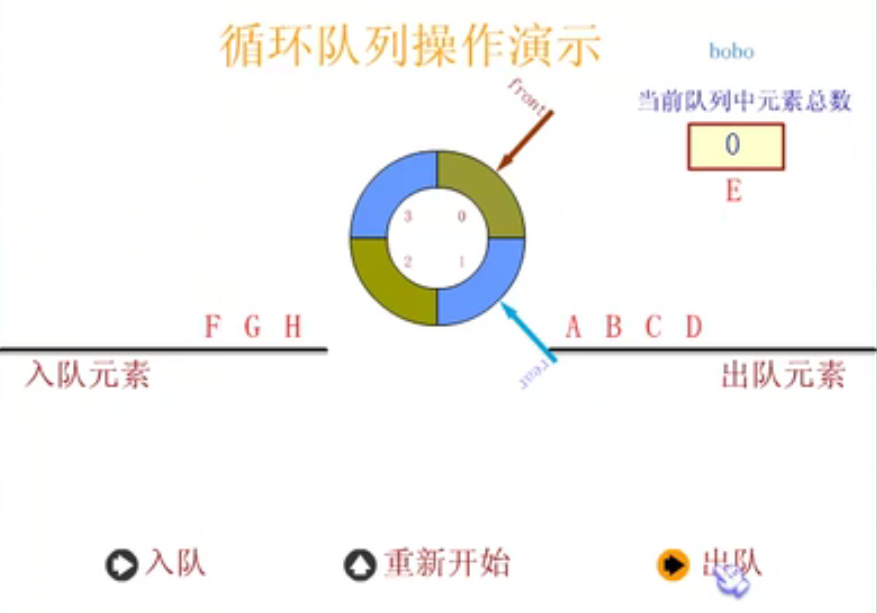
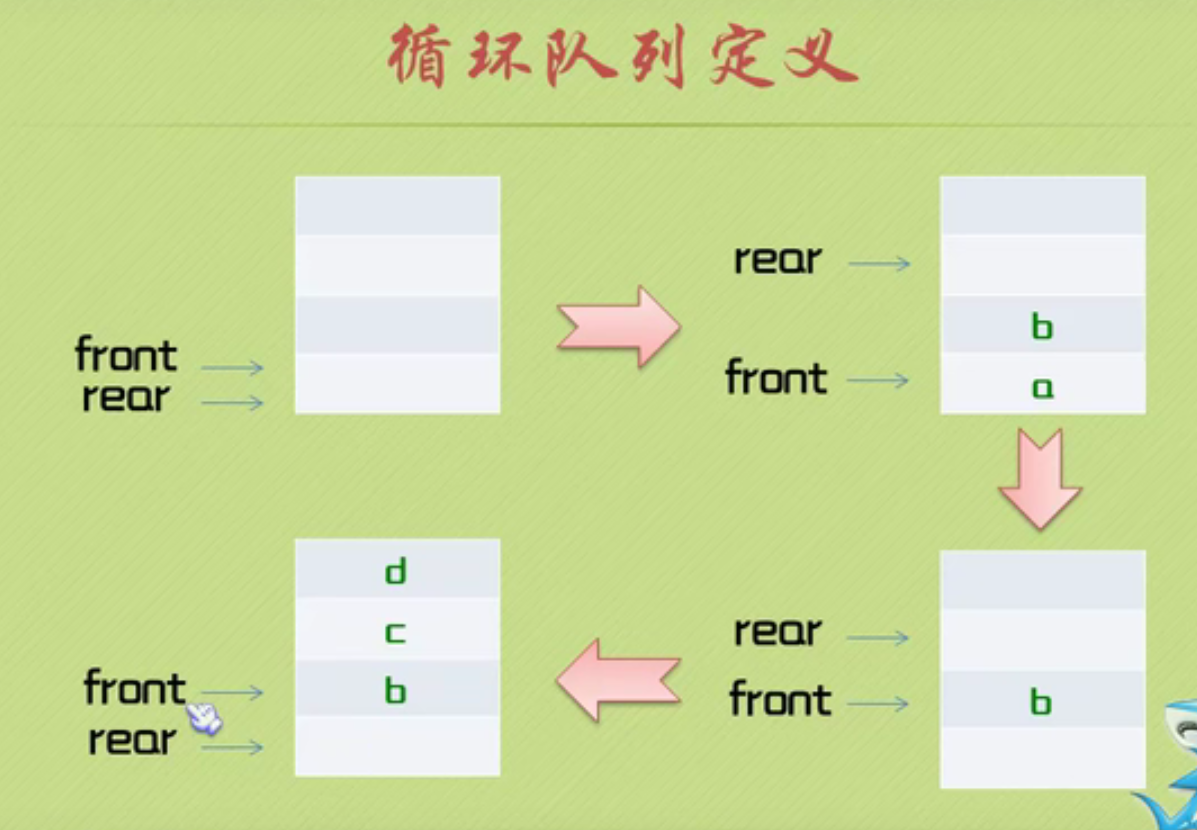

Define circular queue

Initialize circular queue

Queued operation



#include <iostream>
using namespace std;
#define MAXSIZE 100
typedef int ElemType;
typedef struct cycleQueue
{
ElemType *base;
int front;
int rear;//Indicates where it can be used
}cycleQueue;
/**
* Initialize circular queue
* @param q
*/
void initLoopQueue(cycleQueue *q)
{
q->base=( ElemType *) malloc(MAXSIZE*sizeof (ElemType));
if(!q->base)
{
exit(0);
}
q->front=q->rear=0;
}
/**
* Queue
* @param q
* @param e
*/
void InsertQueue(cycleQueue *q,ElemType e)
{
if((q->rear+1)%MAXSIZE==q->front)
{
return;//The queue is full
}
q->base[q->front]=e;
q->rear=(q->rear+1)%MAXSIZE;
}
/**
* Out of queue
* @param q
* @param e
*/
void DeleteQueue(cycleQueue *q,ElemType *e)
{
if(q->front==q->rear)
{
return;//Queue empty
}
*e=q->base[q->front];
q->front=(q->front+1)%MAXSIZE;
}
int main() {
std::cout << "Hello, World!" << std::endl;
return 0;
}
Recursion and divide and conquer


Recursive implementation of Fibonacci sequence

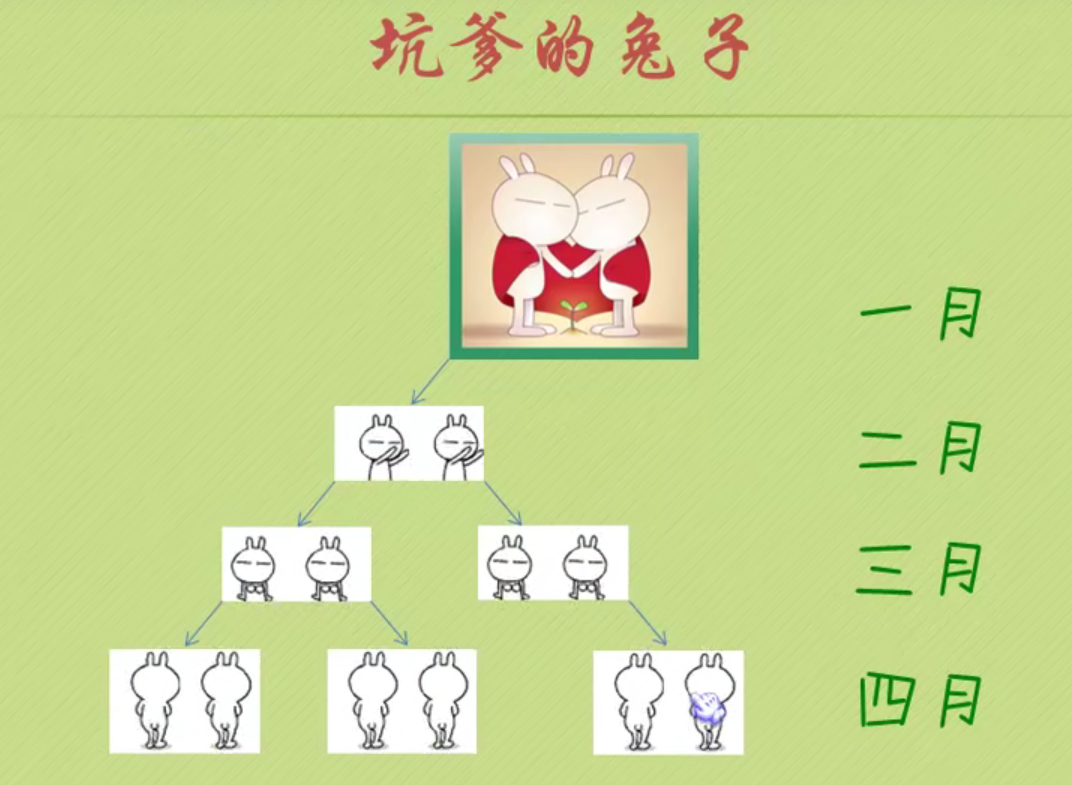



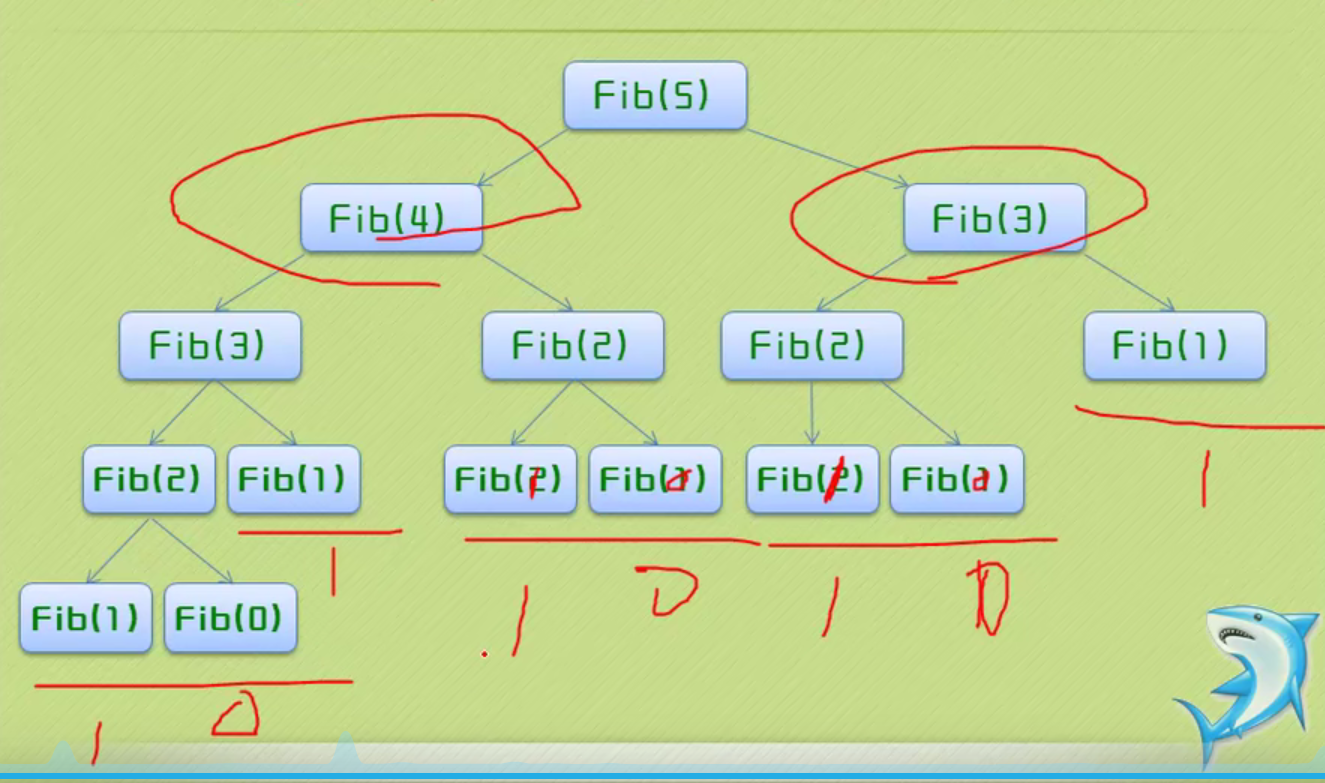
#include <iostream>
using namespace std;
void iter()
{
int a[40];
a[0]=0;
a[1]=1;
cout<<a[0]<<" ";
cout<<a[1]<<" ";
for(int i=2;i<40;i++)
{
a[i]=a[i-1]+a[i-2];
cout<<a[i]<<" ";
}
}
int DiGui_Fib(int n)
{
if(n<2)
{
return n==0?0:1;
}
else
{
return DiGui_Fib(n-1)+ DiGui_Fib(n-2);
}
}
int main() {
iter();
int a =DiGui_Fib(39);
cout<<a<<endl;
return 0;
}
Recursive definition



example


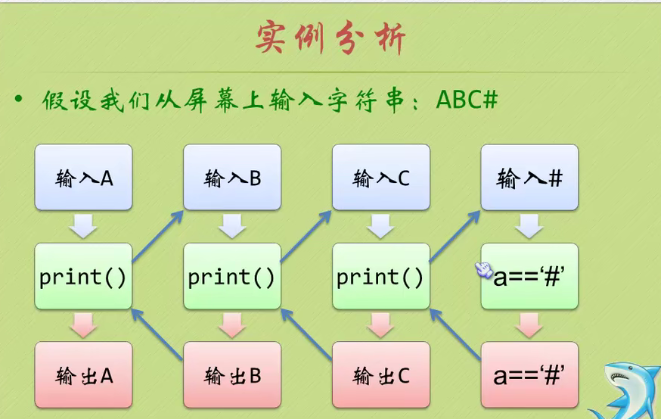
void DiGui_StrInverse()
{
char c;
scanf("%c",&c);
if('#'!=c) DiGui_StrInverse();
if('#'!=c) cout<<c;
}
Partition thought

Recursive implementation of half search method



#include <iostream>
using namespace std;
void iter()
{
int a[40];
a[0]=0;
a[1]=1;
cout<<a[0]<<" ";
cout<<a[1]<<" ";
for(int i=2;i<40;i++)
{
a[i]=a[i-1]+a[i-2];
cout<<a[i]<<" ";
}
}
int DiGui_Fib(int n)
{
if(n<2)
{
return n==0?0:1;
}
else
{
return DiGui_Fib(n-1)+ DiGui_Fib(n-2);
}
}
void DiGui_StrInverse()
{
char c;
scanf("%c",&c);
if('#'!=c) DiGui_StrInverse();
if('#'!=c) cout<<c;
}
/**
* Binary recursive search
* @param str
* @param low
* @param high
* @param k
* @return
*/
int binary_Search_DiGui(int str[],int low,int high,int k)
{
if(low>high)
{
return -1;
}
else
{
int mid = (low+high)/2;
if(str[mid]==k)
{
return mid;
}
if(str[mid]<k)
{
return binary_Search_DiGui(str,mid+1,high,k);
}
else
{
return binary_Search_DiGui(str,low,mid-1,k);
}
}
}
int main() {
/*iter();Fibonacci sequence iteration
int a =DiGui_Fib(39);//Fibonacci sequence recursion
cout<<a<<endl;*/
//DiGui_StrInverse();
//Binary search recursion
int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
int n, addr;
printf("Please enter the keyword to be found: ");
scanf("%d", &n);
addr= binary_Search_DiGui(str,0,10,n);
if( -1 != addr )
{
printf("Find success, Congratulations, Coca Cola! keyword %d The location is: %d\n", n, addr);
}
else
{
printf("Search failed!\n");
}
return 0;
}
Hanoi







#include <iostream>
using namespace std;
void iter()
{
int a[40];
a[0]=0;
a[1]=1;
cout<<a[0]<<" ";
cout<<a[1]<<" ";
for(int i=2;i<40;i++)
{
a[i]=a[i-1]+a[i-2];
cout<<a[i]<<" ";
}
}
int DiGui_Fib(int n)
{
if(n<2)
{
return n==0?0:1;
}
else
{
return DiGui_Fib(n-1)+ DiGui_Fib(n-2);
}
}
/**
*
*/
void Febonaci_test()
{
iter();
int a =DiGui_Fib(39);//Fibonacci sequence recursion
cout<<a<<endl;
}
/**
*
*/
void DiGui_StrInverse()
{
char c;
scanf("%c",&c);
if('#'!=c) DiGui_StrInverse();
if('#'!=c) cout<<c;
}
/**
* Binary recursive search
* @param str
* @param low
* @param high
* @param k
* @return
*/
int binary_Search_DiGui(int str[],int low,int high,int k)
{
if(low>high)
{
return -1;
}
else
{
int mid = (low+high)/2;
if(str[mid]==k)
{
return mid;
}
if(str[mid]<k)
{
return binary_Search_DiGui(str,mid+1,high,k);
}
else
{
return binary_Search_DiGui(str,low,mid-1,k);
}
}
}
void binary_Search_DiGui_test()
{
//Binary search recursion
int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
int n, addr;
printf("Please enter the keyword to be found: ");
scanf("%d", &n);
addr= binary_Search_DiGui(str,0,10,n);
if( -1 != addr )
{
printf("Find success, Congratulations, Coca Cola! keyword %d The location is: %d\n", n, addr);
}
else
{
printf("Search failed!\n");
}
}
/**
* Move n plates from x to z by means of y
* @param n
* @param x
* @param y
* @param z
*/
void move(int n,char x,char y,char z)
{
if(1==n)
{
cout<<x<<"-->"<<z<<" ";
}
else
{
move(n-1,x,z,y);//First move the first n-1 from x to y by means of z
cout<<x<<"-->"<<z<<" ";//Then move the bottom nth to z
move(n-1,y,x,z);//Finally, move the n-1 plates on y to z with the help of x
}
}
/**
* Hanoi
*/
void HanNuoTa()
{
cout<<"Please enter the number of floors of Hanoi Tower:"<<endl;
int n;
cin>>n;
cout<<"The moving steps are as follows:"<<endl;
move(n,'X','Y','Z');
}
int main() {
HanNuoTa();
return 0;
}
//Taking the three-story Hanoi tower as an example, the recursive process is as follows:
3 x y z
{
2 x z y
{
1 x y z x-->z
x-->y
1 z x y z-->y
}
x-->z
2 y x z
{
1 y z x y-->x
y-->z
1 x y z x-->z
}
}
//The final result is:
x-->z
x-->y
z-->y
x-->z
y-->x
y-->z
x-->z
No matter how many layers, in essence, it can recurse to 1, then return to 2, and then return to n-1 again.
Eight queens problem

#include <iostream>
using namespace std;
int count=0;//Count the number of eight queens
/**
* Judge whether there is a queen at the slash position of [row,j]
* @param row
* @param j
* @param chess
* @return
*/
int notDanger(int row,int j,int (*chess)[8])
{
int i,k,flag1=0,flag2=0,flag3=0,flag4=0,flag5=0;
//Judge whether there is danger in all directions
// Determine column direction
for( i=0; i < 8; i++ )
{
if( *(*(chess+i)+j) != 0 )
{
flag1 = 1;
break;
}
}
//Judge upper left
for(i=row,k=j;i>=0&&k>=0;i--,k--)
{
if( *(*(chess+i)+k) != 0 )
{
flag2 = 1;
break;
}
}
// Judge lower right
for( i=row, k=j; i<8 && k<8; i++, k++ )
{
if( *(*(chess+i)+k) != 0 )
{
flag3 = 1;
break;
}
}
// Judge upper right
for( i=row, k=j; i>=0 && k<8; i--, k++ )
{
if( *(*(chess+i)+k) != 0 )
{
flag4 = 1;
break;
}
}
// Judge lower left
for( i=row, k=j; i<8 && k>=0; i++, k-- )
{
if( *(*(chess+i)+k) != 0 )
{
flag5 = 1;
break;
}
}
if(flag1 || flag2 || flag3 || flag4 || flag5)
{
return 0;
}
else
{
return 1;
}
}
/**
* Eight queens recursive implementation, in fact, a good understanding is to use recursion to automatically traverse each line
* @param row Represents the starting line
* @param n Indicates the number of columns
* @param chess Pointer to each line of the chessboard
*/
void EightQueen(int row,int n,int (*chess)[8])//chess points to each row
{
int chess2[8][8],i,j;
//Assign chess2 the value of chessboard chess
for(i=0;i<8;i++)
{
for(j=0;j<8;j++)
{
chess2[i][j]=chess[i][j];
}
}
if(row==8)
{
cout<<"The first"<<count+1<<"species"<<endl;
for(i=0;i<8;i++)
{
for(j=0;j<8;j++)
{
cout<<*(*(chess2+i)+j);
}
cout<<endl;
}
cout<<endl;
count++;
}
else
{
//Judge whether this position is dangerous
//If there is no danger, go on
for(j=0;j<n;j++)
{
if(notDanger(row,j,chess)) //Judge whether this position is dangerous
{
for(i=0;i<8;i++)
{
*(*(chess2+row)+i)=0;//Mark the entire column as 0 first
}
*(*(chess2+row)+j)=1;//Then mark the non dangerous position as 1 -- that is, the position of the queen
EightQueen(row+1,n,chess2);
}
}
}
};
void EightQueen_test()
{
int chess[8][8];
for(int i=0;i<8;i++)
{
for(int j=0;j<8;j++)
{
chess[i][j]=0;//Initialize chessboard
}
}
EightQueen(0,8,chess);
}
int main()
{
EightQueen_test();
return 0;
}
Here is the complete recursive divide and conquer Code:
#include <iostream>
using namespace std;
void iter()
{
int a[40];
a[0]=0;
a[1]=1;
cout<<a[0]<<" ";
cout<<a[1]<<" ";
for(int i=2;i<40;i++)
{
a[i]=a[i-1]+a[i-2];
cout<<a[i]<<" ";
}
}
int DiGui_Fib(int n)
{
if(n<2)
{
return n==0?0:1;
}
else
{
return DiGui_Fib(n-1)+ DiGui_Fib(n-2);
}
}
/**
*
*/
void Febonaci_test()
{
iter();
int a =DiGui_Fib(39);//Fibonacci sequence recursion
cout<<a<<endl;
}
/**
*
*/
void DiGui_StrInverse()
{
char c;
scanf("%c",&c);
if('#'!=c) DiGui_StrInverse();
if('#'!=c) cout<<c;
}
/**
* Binary recursive search
* @param str
* @param low
* @param high
* @param k
* @return
*/
int binary_Search_DiGui(int str[],int low,int high,int k)
{
if(low>high)
{
return -1;
}
else
{
int mid = (low+high)/2;
if(str[mid]==k)
{
return mid;
}
if(str[mid]<k)
{
return binary_Search_DiGui(str,mid+1,high,k);
}
else
{
return binary_Search_DiGui(str,low,mid-1,k);
}
}
}
void binary_Search_DiGui_test()
{
//Binary search recursion
int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
int n, addr;
printf("Please enter the keyword to be found: ");
scanf("%d", &n);
addr= binary_Search_DiGui(str,0,10,n);
if( -1 != addr )
{
printf("Find success, Congratulations, Coca Cola! keyword %d The location is: %d\n", n, addr);
}
else
{
printf("Search failed!\n");
}
}
/**
* Move n plates from x to z by means of y
* @param n
* @param x
* @param y
* @param z
*/
void move(int n,char x,char y,char z)
{
if(1==n)
{
cout<<x<<"-->"<<z<<" ";
}
else
{
move(n-1,x,z,y);//First move the first n-1 from x to y by means of z
cout<<x<<"-->"<<z<<" ";//Then move the bottom nth to z
move(n-1,y,x,z);//Finally, move the n-1 plates on y to z with the help of x
}
}
/**
* Hanoi
*/
void HanNuoTa()
{
cout<<"Please enter the number of floors of Hanoi Tower:"<<endl;
int n;
cin>>n;
cout<<"The moving steps are as follows:"<<endl;
move(n,'X','Y','Z');
}
int count=0;//Count the number of eight queens
/**
* Judge whether there is a queen at the slash position of [row,j]
* @param row
* @param j
* @param chess
* @return
*/
int notDanger(int row,int j,int (*chess)[8])
{
int i,k,flag1=0,flag2=0,flag3=0,flag4=0,flag5=0;
//Judge whether there is danger in all directions
// Determine column direction
for( i=0; i < 8; i++ )
{
if( *(*(chess+i)+j) != 0 )
{
flag1 = 1;
break;
}
}
//Judge upper left
for(i=row,k=j;i>=0&&k>=0;i--,k--)
{
if( *(*(chess+i)+k) != 0 )
{
flag2 = 1;
break;
}
}
// Judge lower right
for( i=row, k=j; i<8 && k<8; i++, k++ )
{
if( *(*(chess+i)+k) != 0 )
{
flag3 = 1;
break;
}
}
// Judge upper right
for( i=row, k=j; i>=0 && k<8; i--, k++ )
{
if( *(*(chess+i)+k) != 0 )
{
flag4 = 1;
break;
}
}
// Judge lower left
for( i=row, k=j; i<8 && k>=0; i++, k-- )
{
if( *(*(chess+i)+k) != 0 )
{
flag5 = 1;
break;
}
}
if(flag1 || flag2 || flag3 || flag4 || flag5)
{
return 0;
}
else
{
return 1;
}
}
/**
* Eight queens recursive implementation, in fact, a good understanding is to use recursion to automatically traverse each line
* @param row Represents the starting line
* @param n Indicates the number of columns
* @param chess Pointer to each line of the chessboard
*/
void EightQueen(int row,int n,int (*chess)[8])//chess points to each row
{
int chess2[8][8],i,j;
//Assign chess2 the value of chessboard chess
for(i=0;i<8;i++)
{
for(j=0;j<8;j++)
{
chess2[i][j]=chess[i][j];
}
}
if(row==8)
{
cout<<"The first"<<count+1<<"species"<<endl;
for(i=0;i<8;i++)
{
for(j=0;j<8;j++)
{
cout<<*(*(chess2+i)+j);
}
cout<<endl;
}
cout<<endl;
count++;
}
else
{
//Judge whether this position is dangerous
//If there is no danger, go on
for(j=0;j<n;j++)
{
if(notDanger(row,j,chess)) //Judge whether this position is dangerous
{
for(i=0;i<8;i++)
{
*(*(chess2+row)+i)=0;//Mark the entire column as 0 first
}
*(*(chess2+row)+j)=1;//Then mark the non dangerous position as 1 -- that is, the position of the queen
EightQueen(row+1,n,chess2);
}
}
}
};
void EightQueen_test()
{
int chess[8][8];
for(int i=0;i<8;i++)
{
for(int j=0;j<8;j++)
{
chess[i][j]=0;//Initialize chessboard
}
}
EightQueen(0,8,chess);
}
int main() {
//HanNuoTa();
EightQueen_test();
return 0;
}
/*Taking the three-story Hanoi tower as an example, the recursive process is as follows:
3 x y z
{
2 x z y
{
1 x y z x-->z
x-->y
1 z x y z-->y
}
x-->z
2 y x z
{
1 y z x y-->x
y-->z
1 x y z x-->z
}
}
The final result is:
x-->z
x-->y
z-->y
x-->z
y-->x
y-->z
x-->z
*/
character string




Storage structure of string

BF algorithm

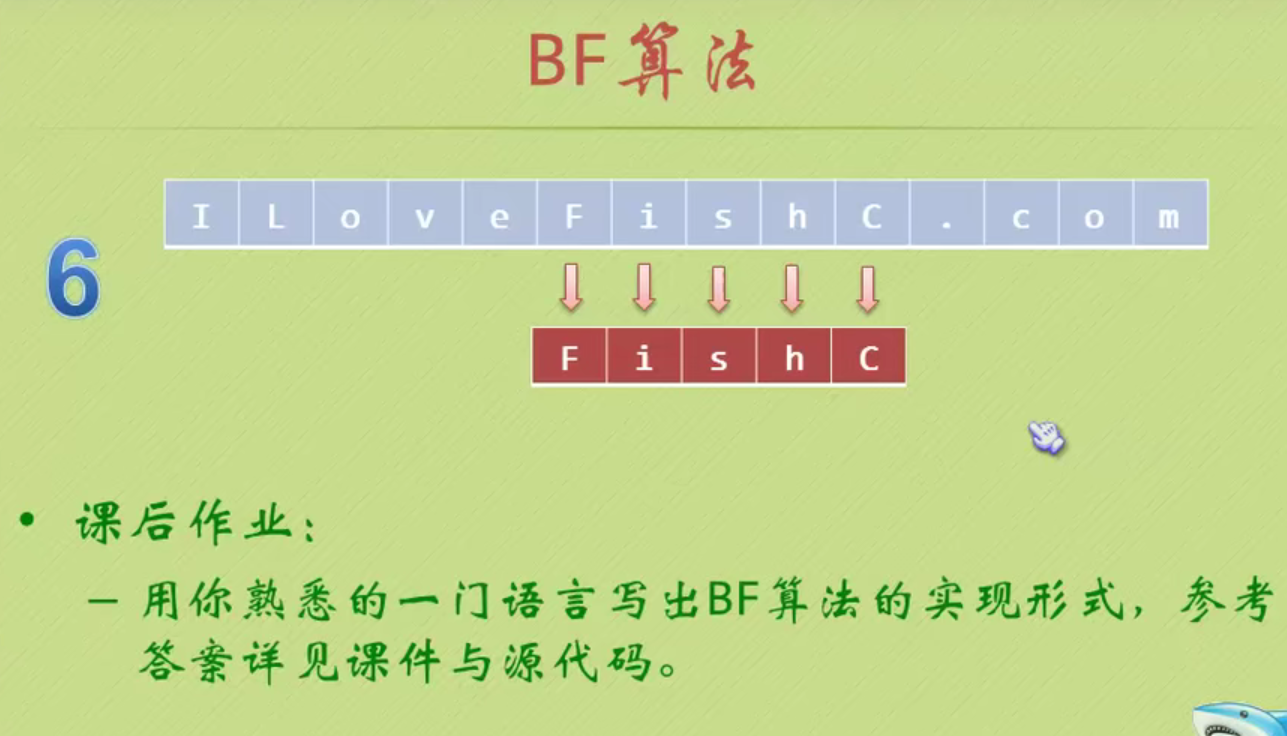
#include <iostream>
#include <string>
using namespace std;
//Violence algorithm classic shape, judge the size of two strings
int compare_Eaual(string &s1,string &s2)
{
int flag=0;
int n1=s1.size();
int n2=s2.size();
n1=max(n1,n2);
for(int i=0;i<n1;i++)
{
if(s1[i]>s2[i])
{
flag=1;
break;
}
else if(s1[i]==s2[i])
{
flag=0;
}
else if(s1[i]<s2[i])
{
flag=-1;
break;
}
}
return flag;
}
int main() {
string s1="aaf";
string s2="abf";
int jue;
jue=compare_Eaual(s1,s2);
if(jue==1)
{
cout<<"s1>s2"<<endl;
}
else if(jue==0)
{
cout<<"s1=s2"<<endl;
}
else if(jue==-1)
{
cout<<"s1<s2"<<endl;
}
return 0;
}
KMP algorithm


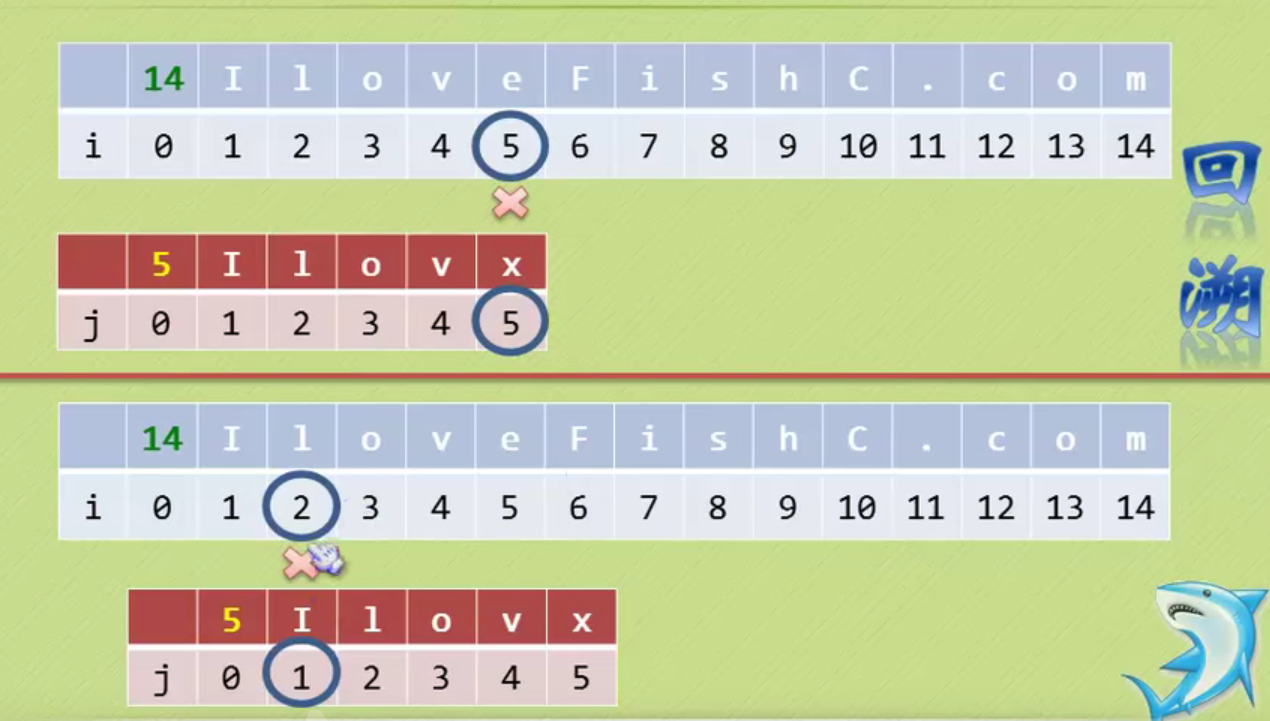


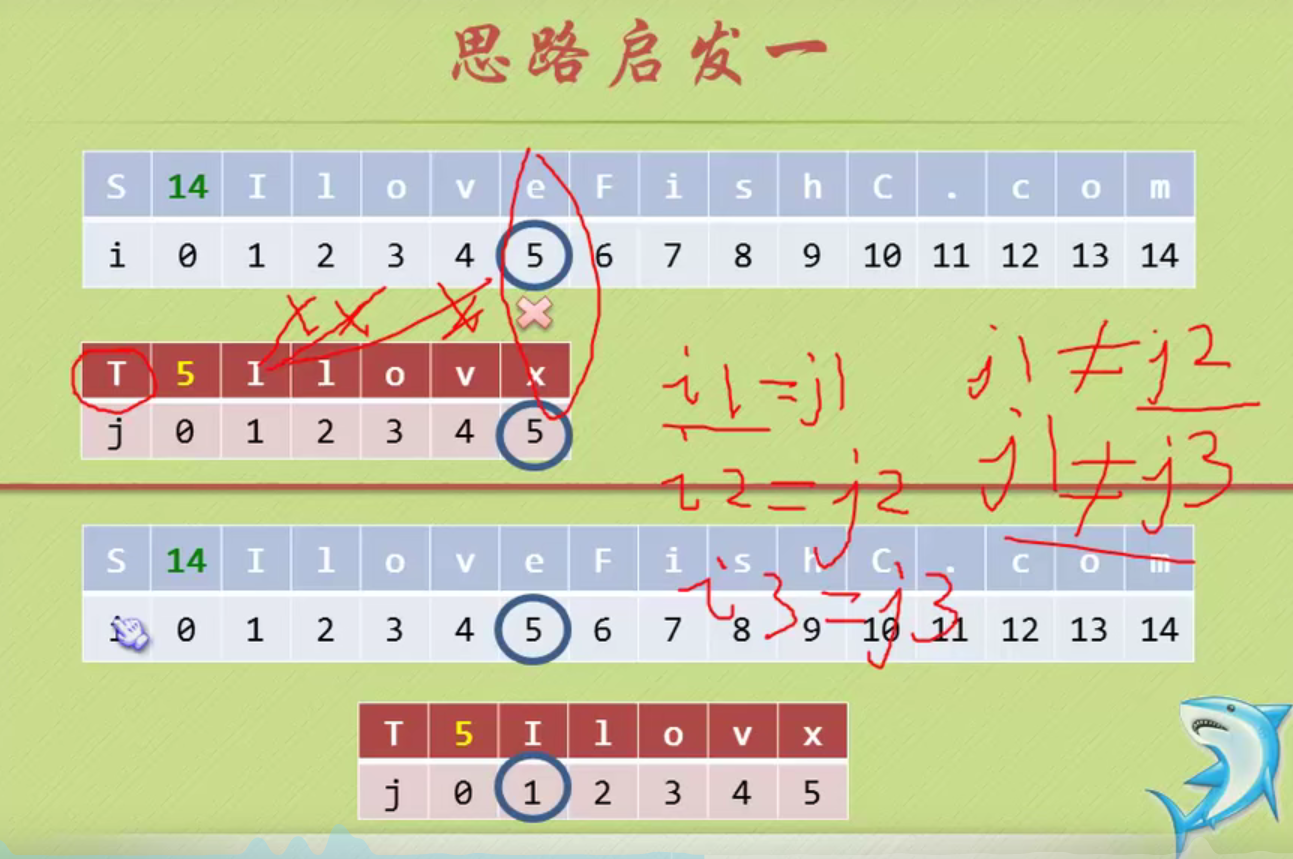
No backtracking is required i
When determining the inequality, there is no same character in front of the pattern string, and the backtracking starts from 1
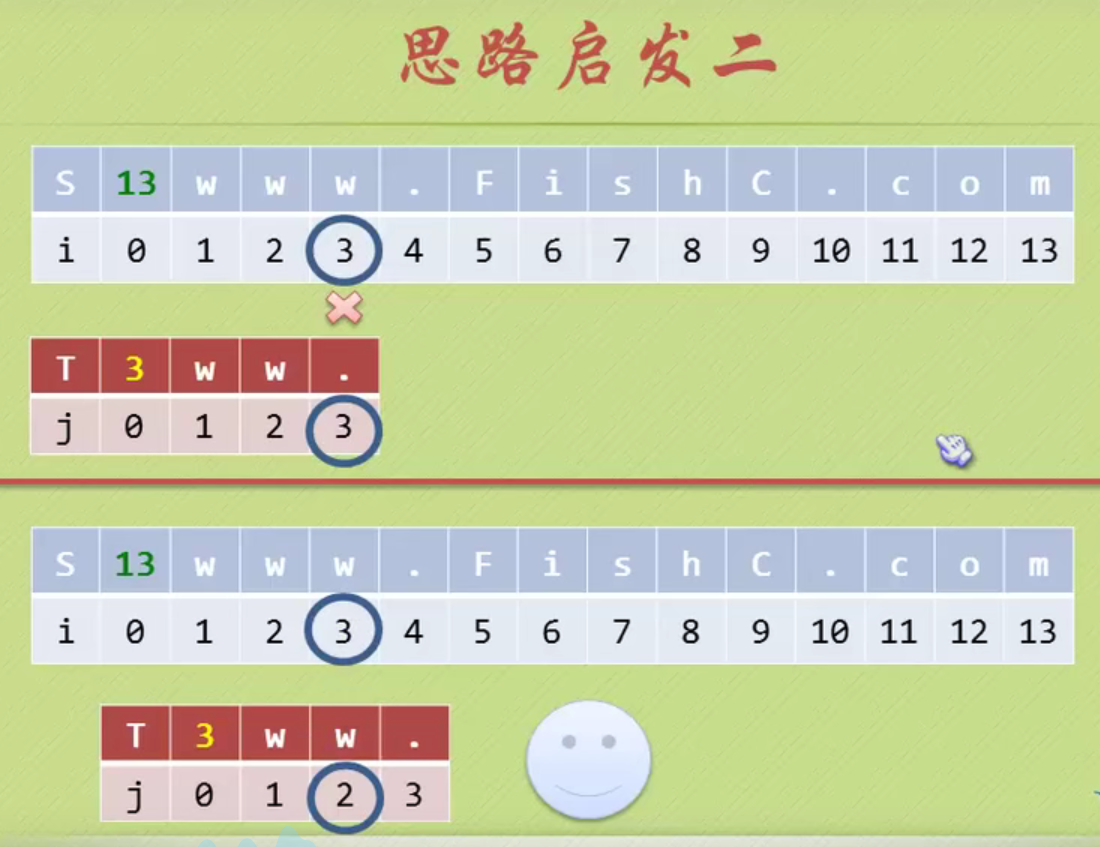
There are two equal characters in the pattern string, and the backtracking starts from 2
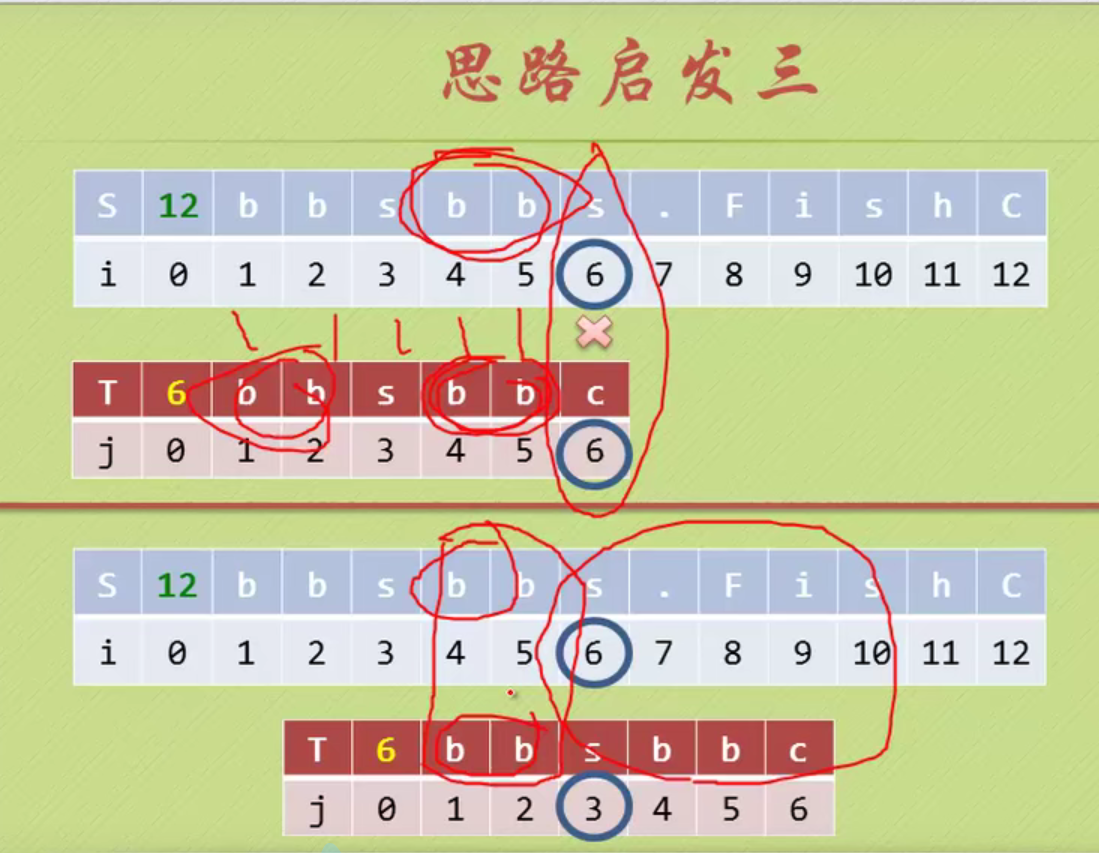
There is a pair of equal characters in the pattern string, and the backtracking starts from 2
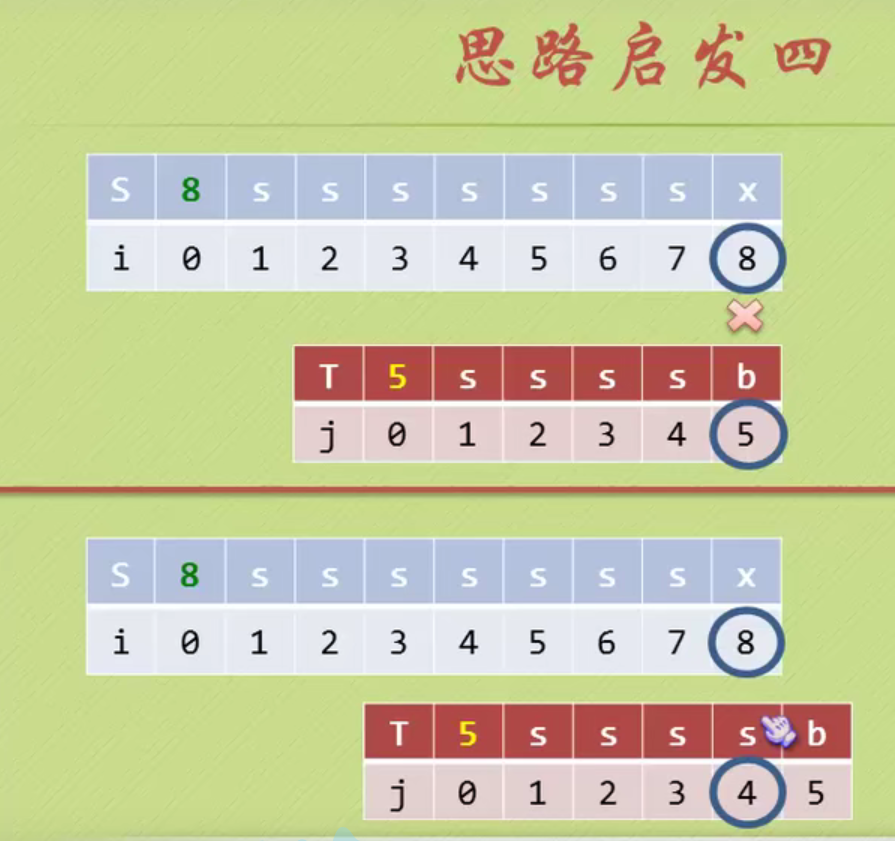


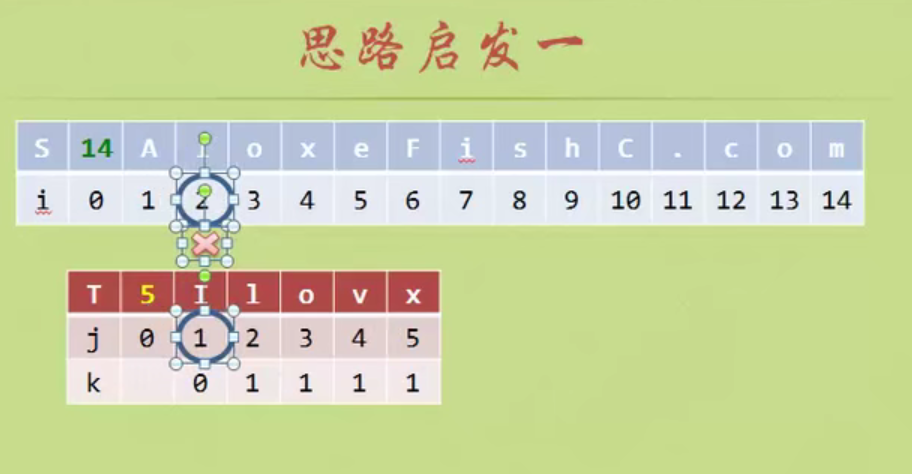

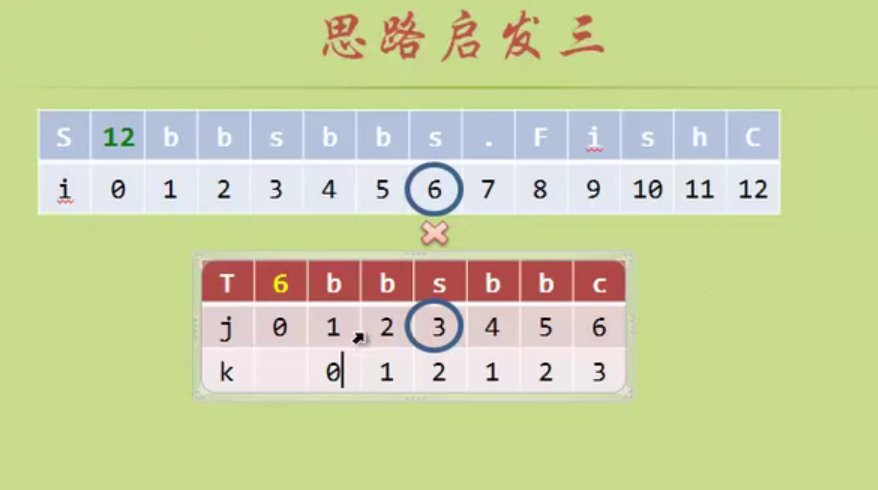
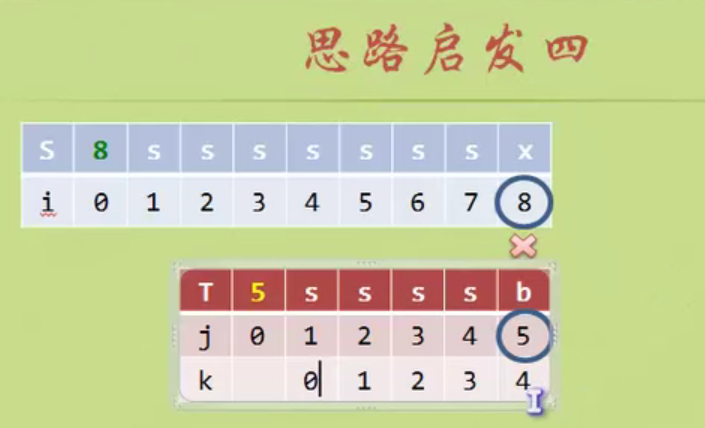
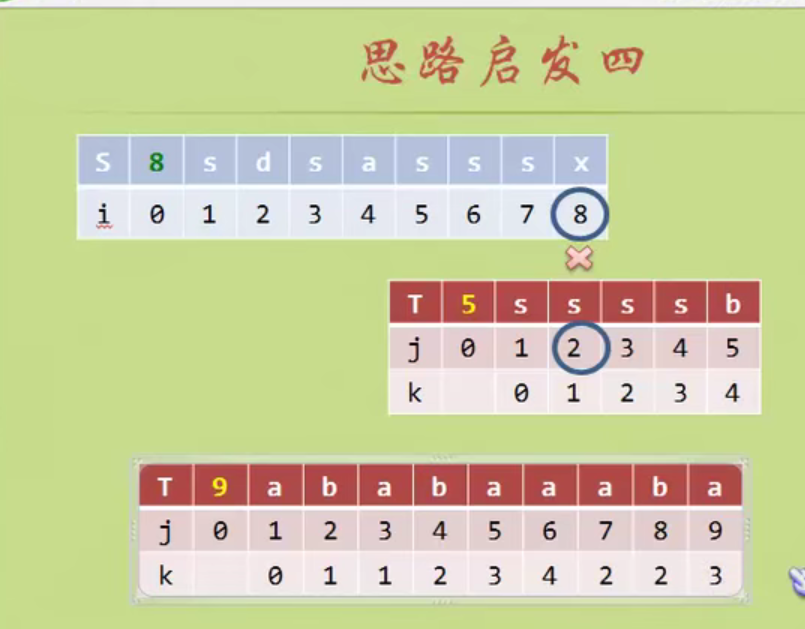
When the matching is unequal, the prefix and suffix of the string formed from the beginning A to the previous position of the matching inequality have several equal characters. Add n equal characters, then j starts from the position of n+1. (Prefix suffix is not A string in position)
Analysis of NEXT array code principle of KMP algorithm
The NEXT array is the K above

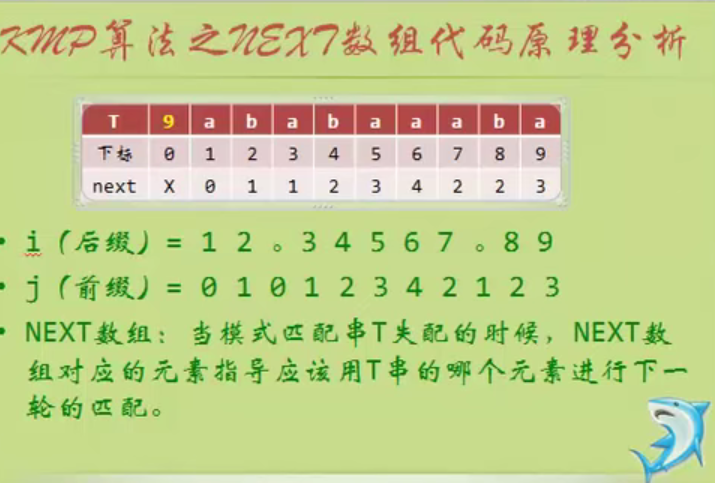
void get_next(string T,int *next)
{
int j=0;
int i=1;
next[1]=0;
while(i<T[0])//When the suffix exceeds the length, the matching is completed
{
if(j==0|| T[i]==T[j])
{
i++;
j++;
next[i]=j;
}
else
{
//j backtracking
j=next[j];
}
//Because the prefix is fixed, the suffix is relative (the prefix is the actual character)
}
}
//Returns the position of string T after the pos character of main string S
//If it does not exist, 0 is returned
int Index_KMP(string S,string T,int pos)
{
int i=pos;
int j=1;
int next[255];
get_next(T,next);//Get next array
while(i<=S[0]&&j<=T[0])//S[0] and T[0] store the length of the string
{
if(j==0|| S[i]==T[j])
{
i++;
j++;
}
else
{
j=next[j];//The soul of KMP algorithm uses next as the highest guide
}
}
//After successful matching, j must be one bit larger than the string of T
if(j>T[0])
{
return i-T[0];
}
else
{
return 0;
}
}
Implementation and optimization of KMP algorithm

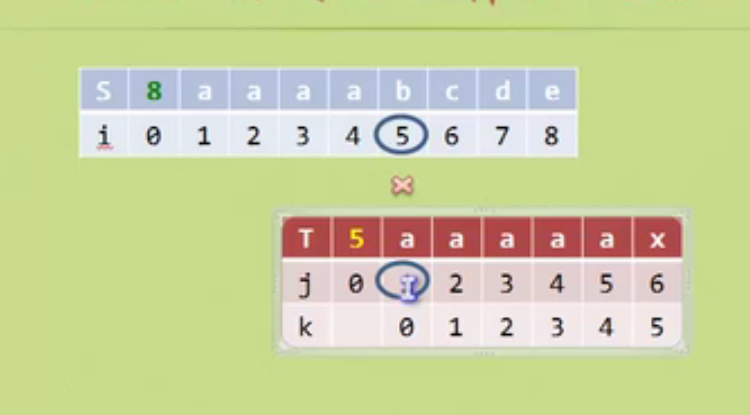
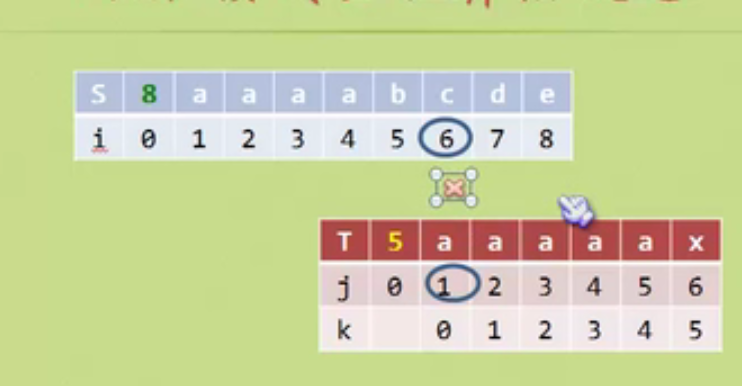
What about this special case
In this way, when it is judged that the position is not equal, if the position is m, then when the character of T in position m-1 and the prefix character are equal, j will directly return to the position corresponding to the prefix, which is back to 0 in the above figure
#include <iostream>
#include <string>
using namespace std;
void get_next(string T,int *next)
{
int j=0;
int i=1;
next[1]=0;
while(i<T[0])//When the suffix exceeds the length, the matching is completed
{
if(j==0|| T[i]==T[j])
{
i++;
j++;
//improvement
if(T[i]!=T[j])
{
next[i]=j;
}
else
{
next[i]=next[j];//Assign prefix
}
}
else
{
//j backtracking
j=next[j];
}
//Because the prefix is fixed, the suffix is relative (the prefix is the actual character)
}
}
//Returns the position of string T after the pos character of main string S
//If it does not exist, 0 is returned
int Index_KMP(string S,string T,int pos)
{
int i=pos;
int j=1;
int next[255];
get_next(T,next);//Get next array
while(i<=S[0]&&j<=T[0])//S[0] and T[0] store the length of the string
{
if(j==0|| S[i]==T[j])
{
i++;
j++;
}
else
{
j=next[j];//The soul of KMP algorithm uses next as the highest guide
}
}
//After successful matching, j must be one bit larger than the string of T
if(j>T[0])
{
return i-T[0];
}
else
{
return 0;
}
}
int main() {
char str[255]=" aaaaax";
int next[255];
int i=1;
str[0]=9;
get_next(str,next);
for(i=1;i<10;i++)
{
cout<<next[i]<<" ";
}
return 0;
}
tree

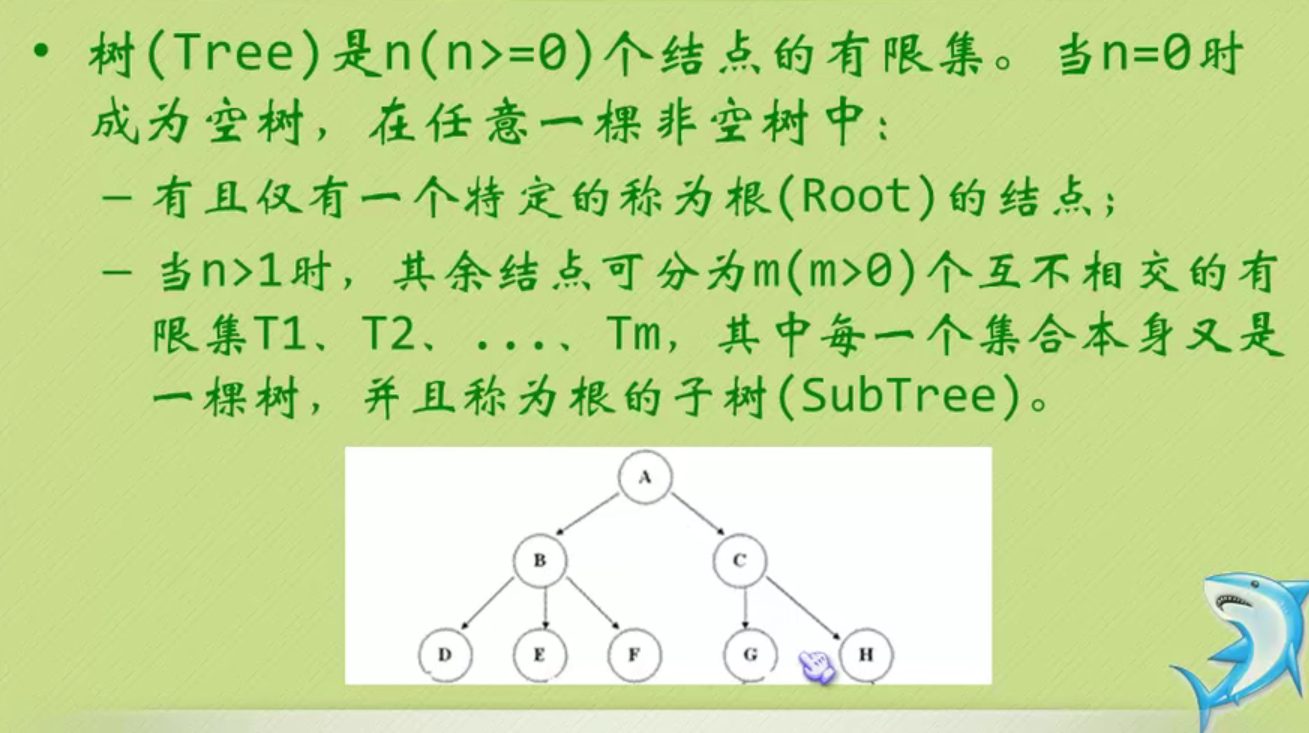
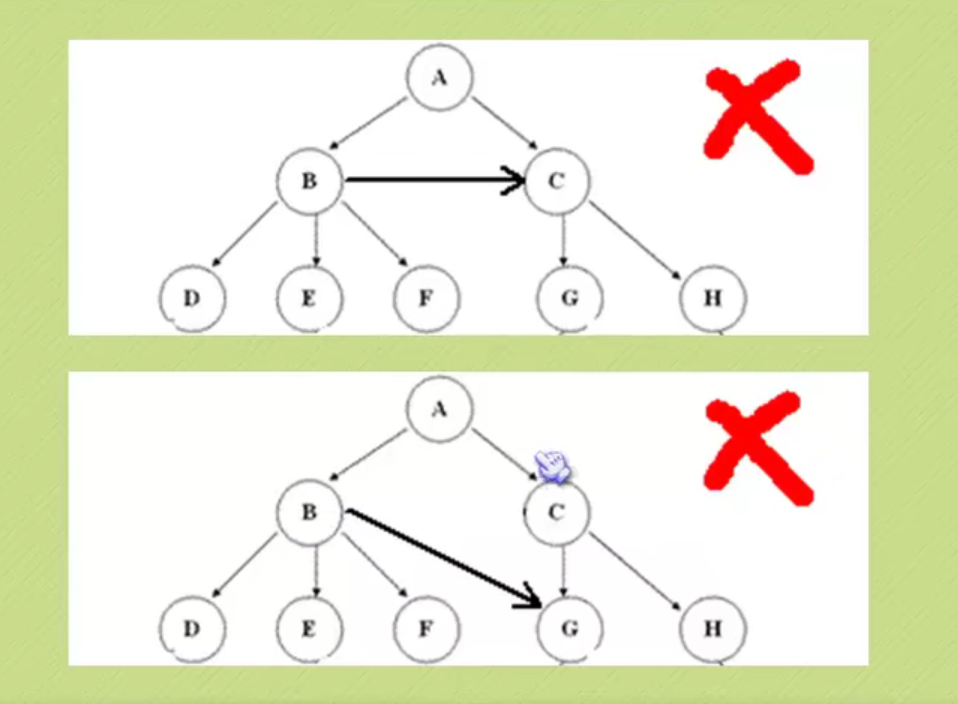

In the figure above, the largest node of the whole tree is 3
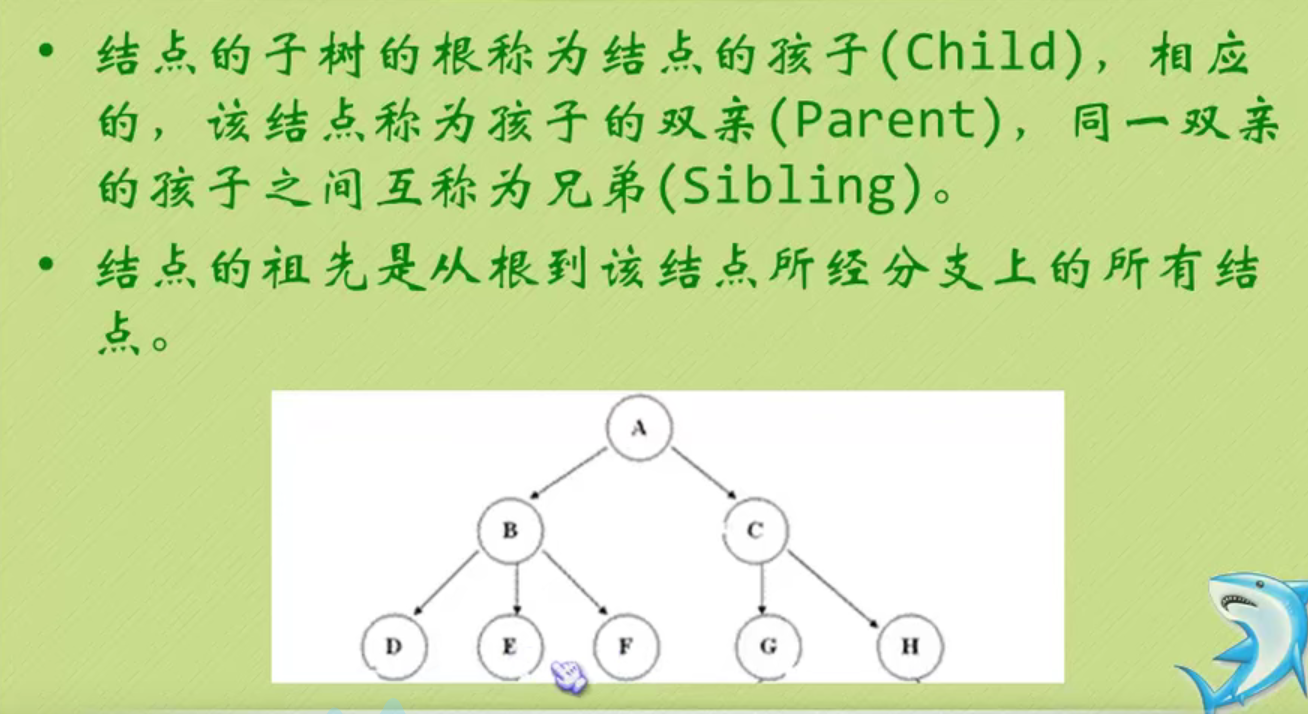
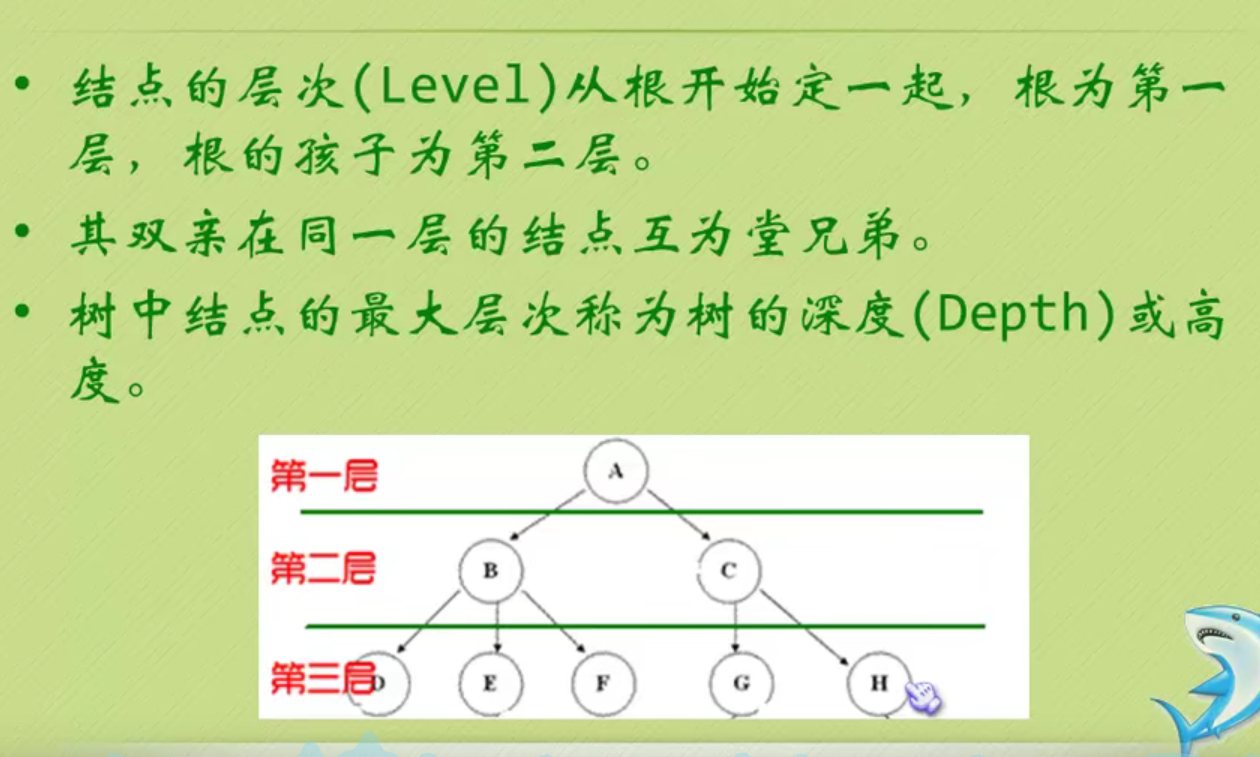
The depth of the tree above is 3 because it has three layers.
Storage structure of tree


// Definition of node structure of parent representation of tree
#define MAX_TREE_SIZE 100
typedef int ElemType;
typedef struct PTNode
{
ElemType data; // Node data
int parent; // Parental position
}PTNode;
typedef struct
{
PTNode nodes[MAX_TREE_SIZE];
int r; // Location of root
int n; // Number of nodes
}PTree;
Parental representation
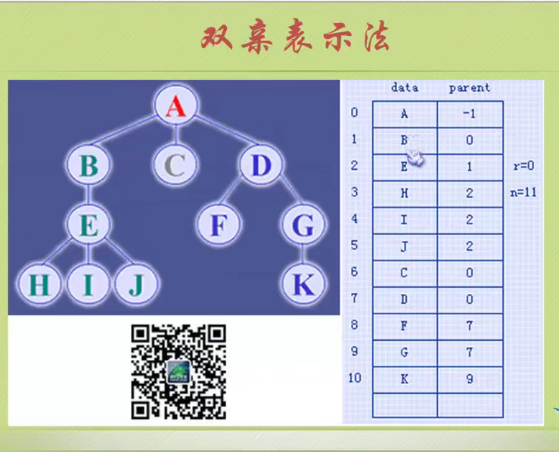
A is a root without parents, so it is - 1

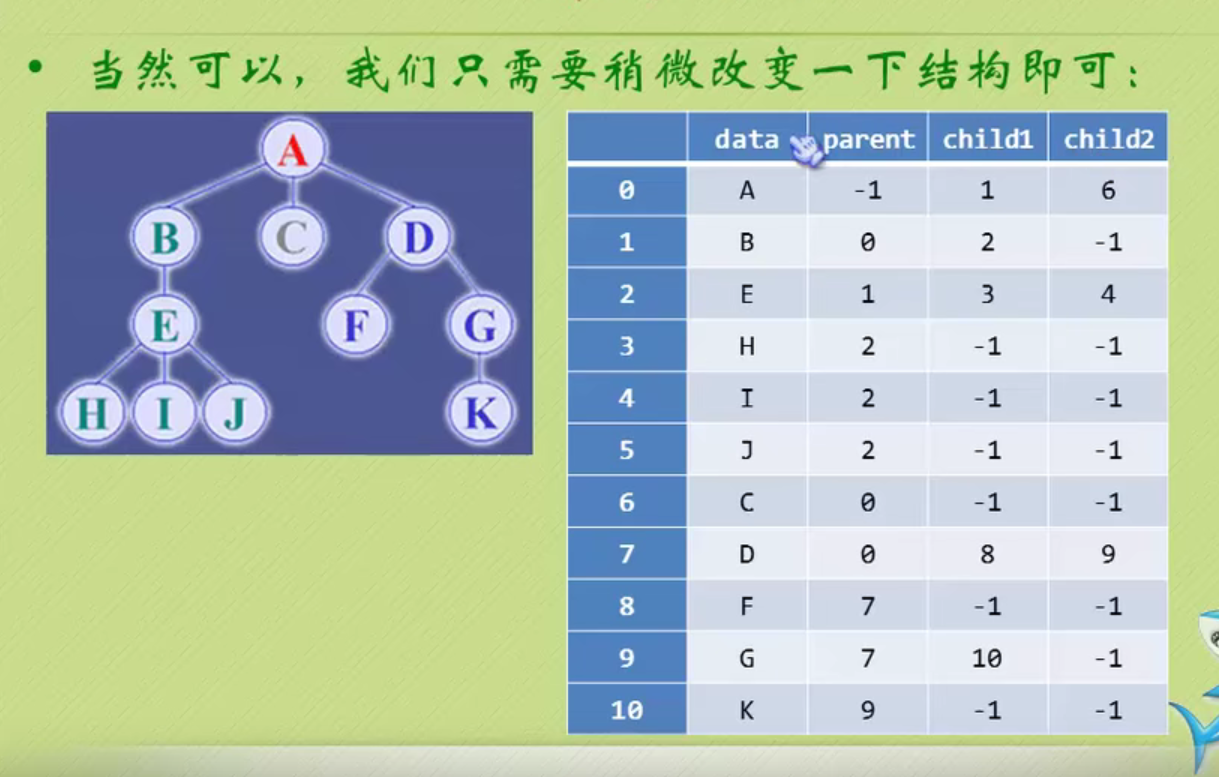
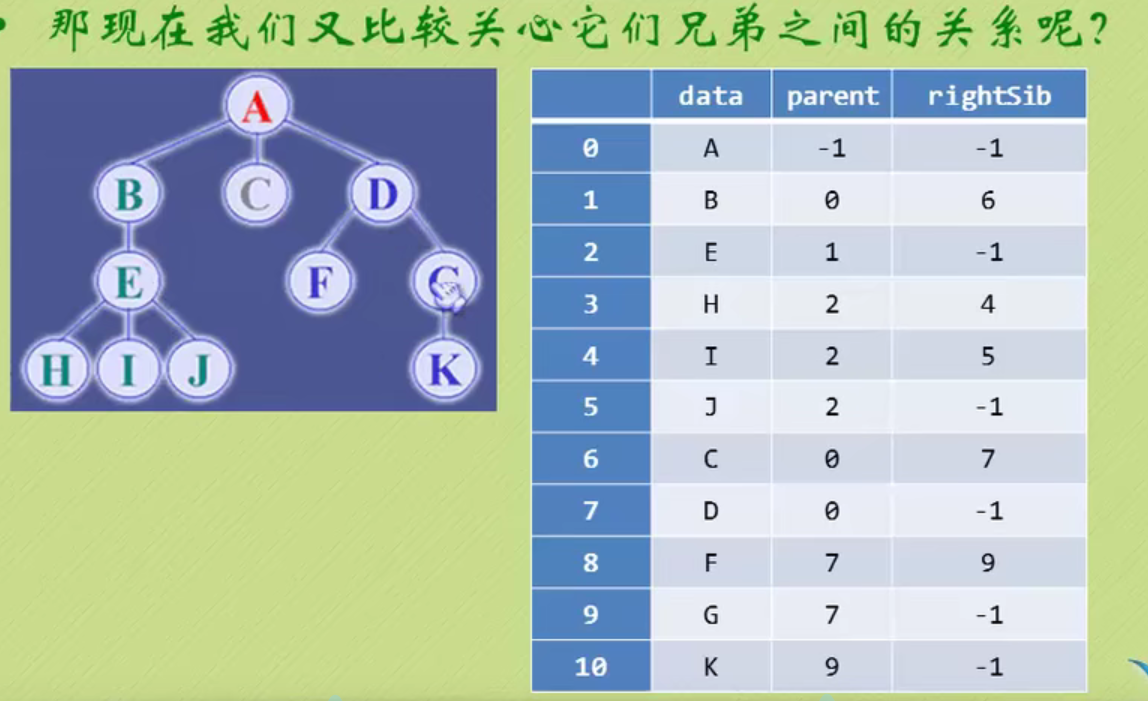
Child representation
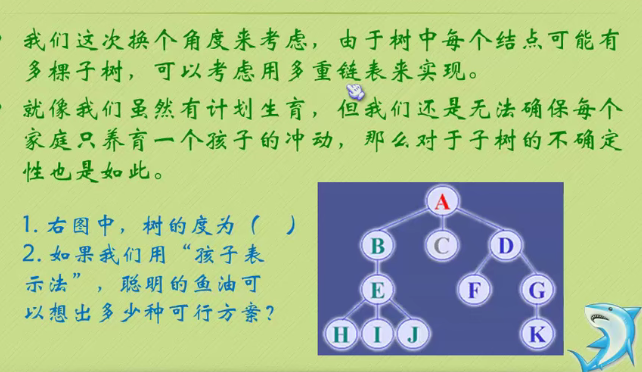
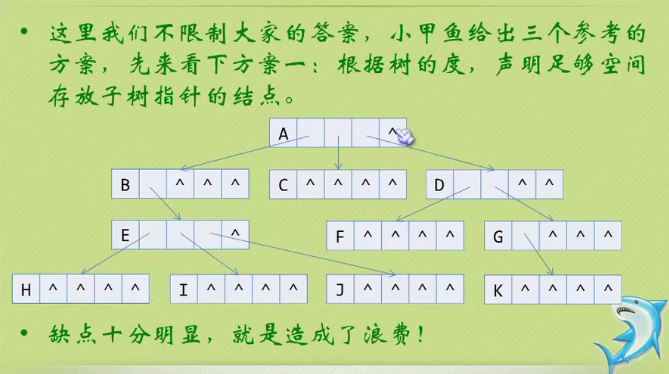
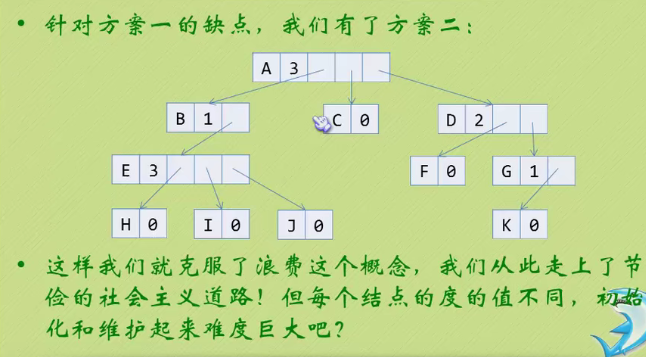
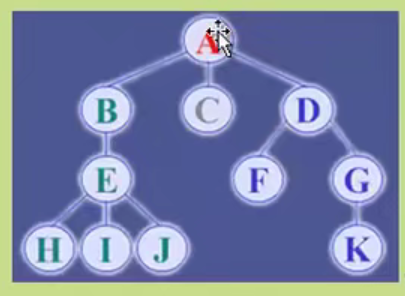
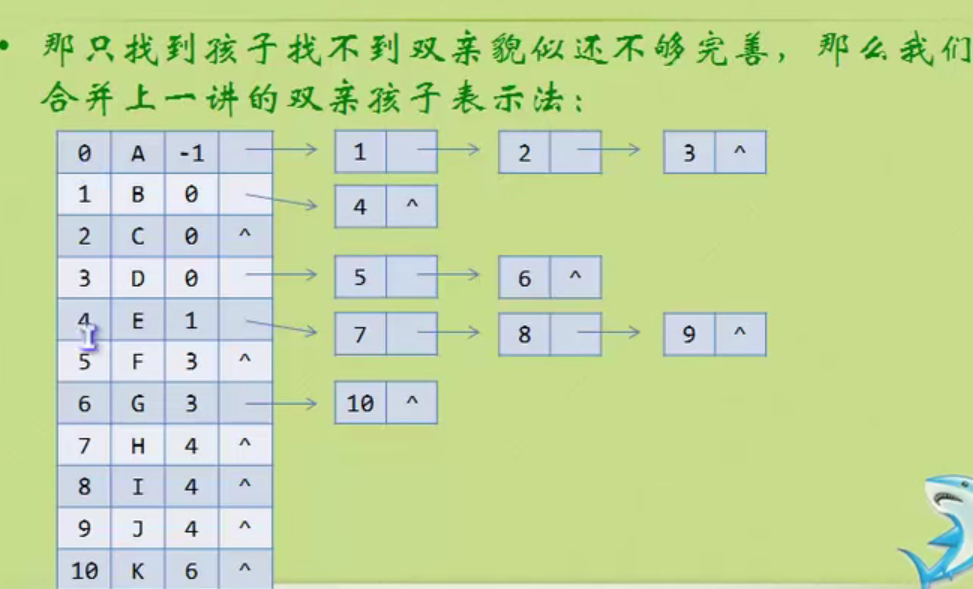
The one on the left is an array, and the one on the right is linked with a chain

#define MAX_TREE_SIZE 100
typedef char ElemType;
//Child node
typedef struct CTNode
{
int child;//Subscript to child node
struct CTNode *next;//Pointer to the next child node
}* Childptr;
//Header structure
typedef struct
{
ElemType data; //Data stored in nodes of tree species
int parent;//Location of parents
Childptr firstchild;//Pointer to the first child
}CTBox;
//Tree structure
typedef struct
{
CTBox nodes[MAX_TREE_SIZE];//Node array
int r;//Location of root
int n;//Number of nodes in the tree
};
Binary tree


Pay attention to distinguish between left subtree and right subtree
Five mentality of binary tree
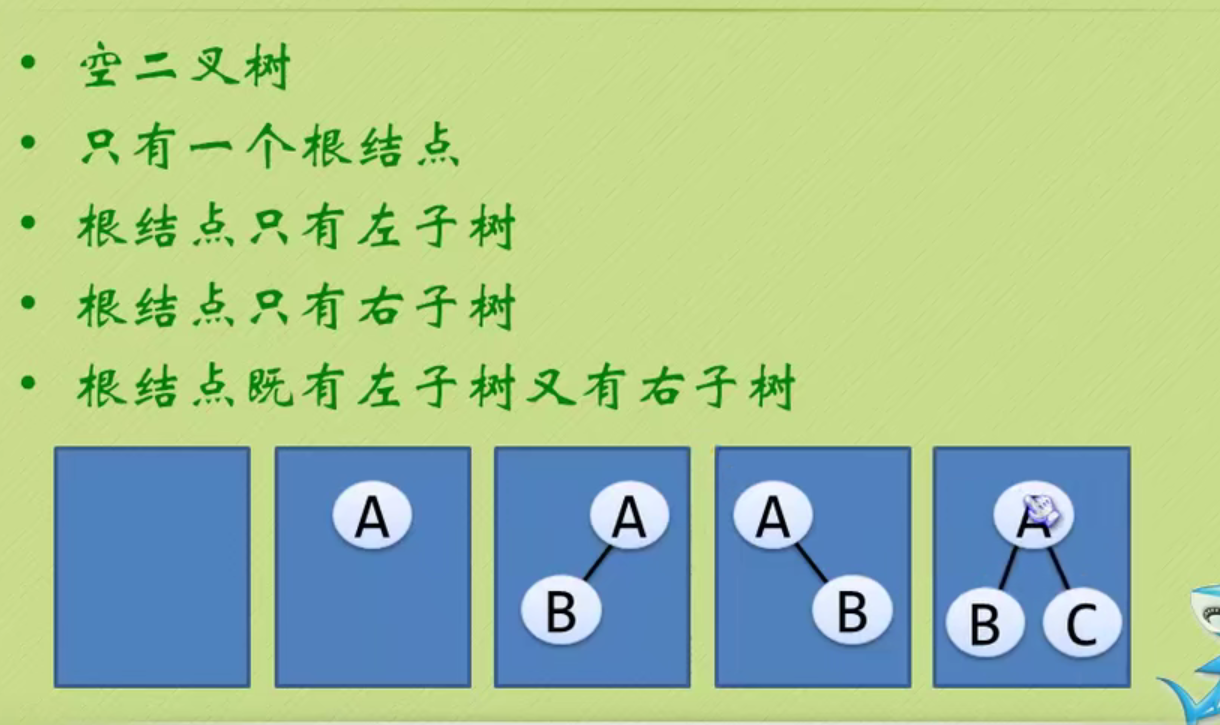
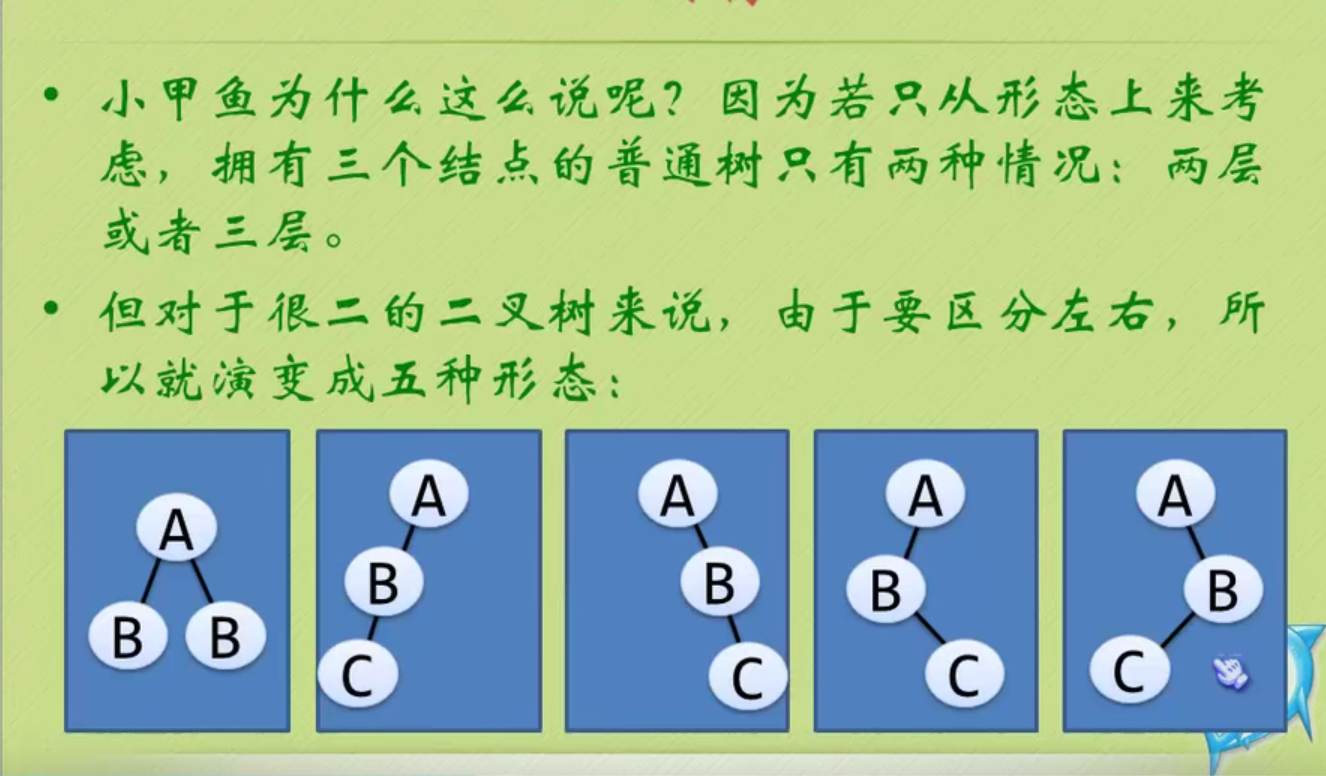
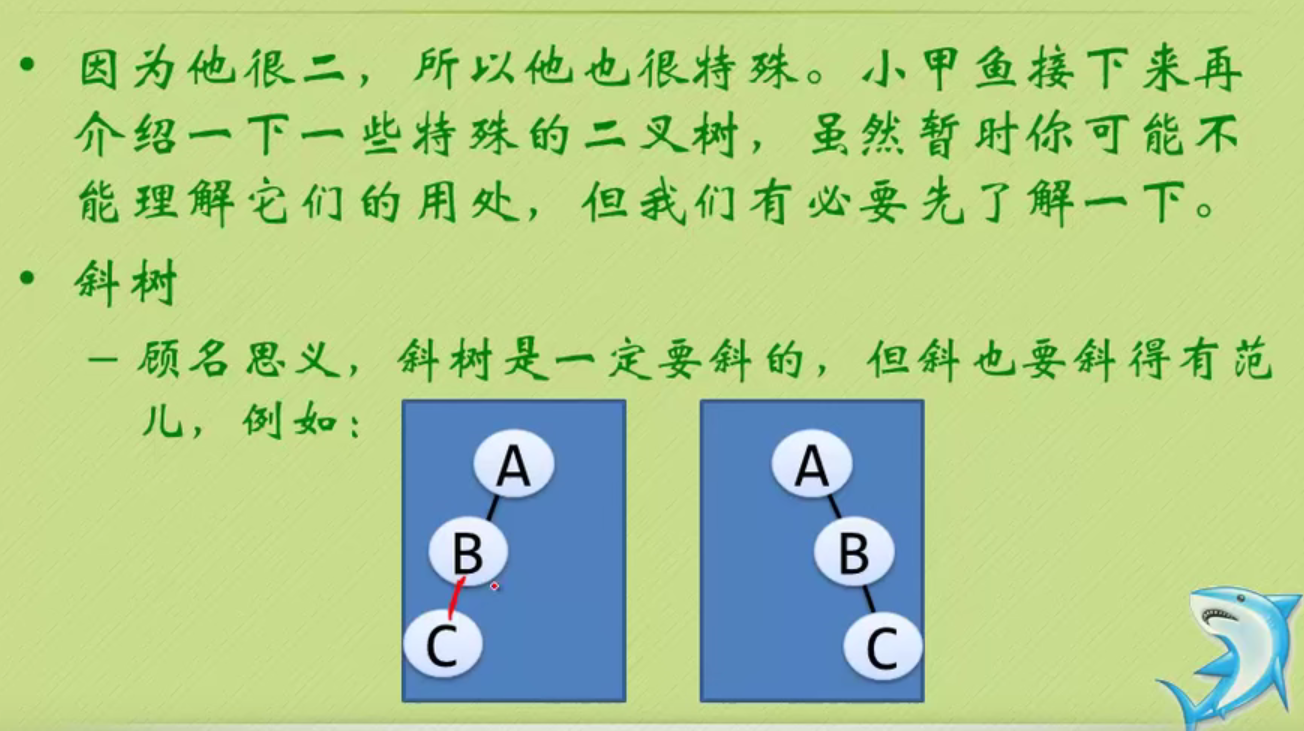
Oblique trees can only lean all to the left or all to the right.

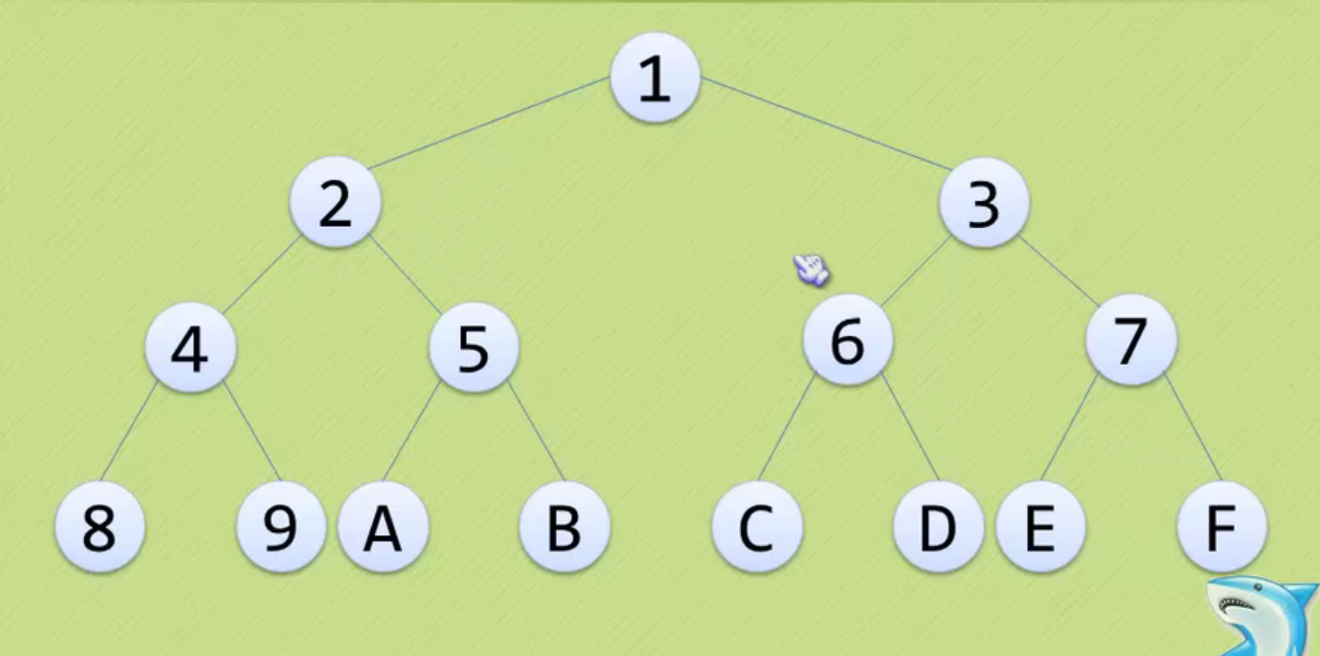

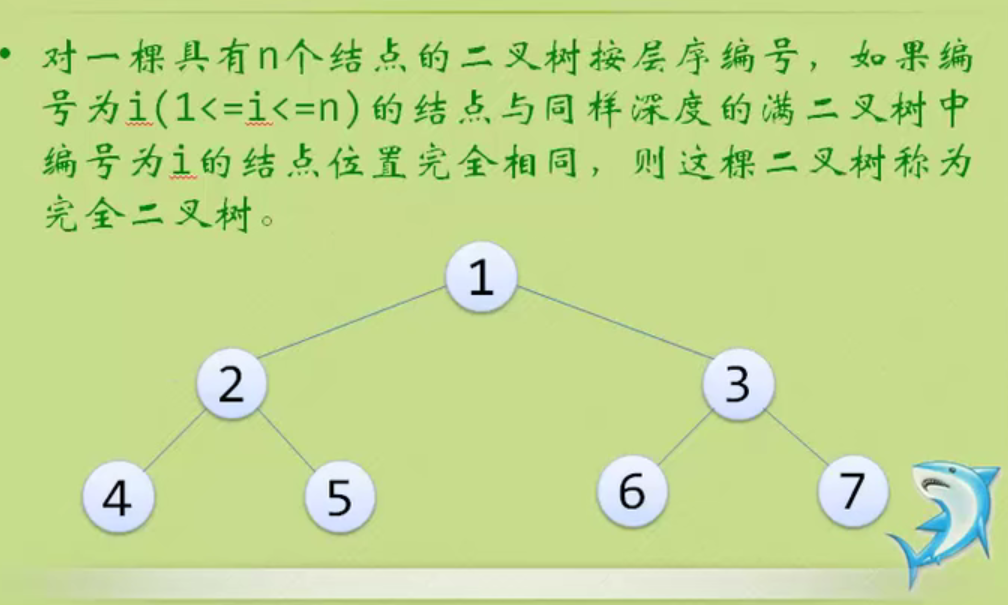
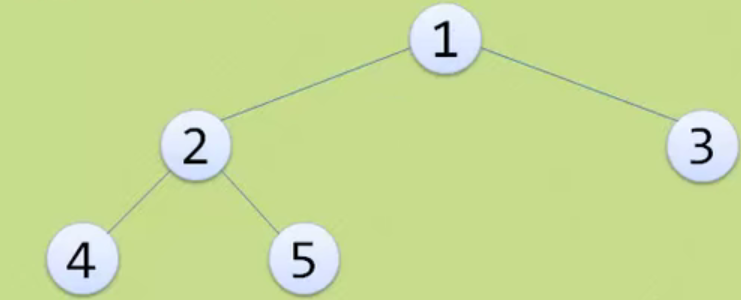
The above figure is still a complete binary tree, but not a full binary tree.
Because the serial numbers above are still connected, 1 2 3 4 5

The above features are reflected in the figure above
None of the following is a complete binary tree
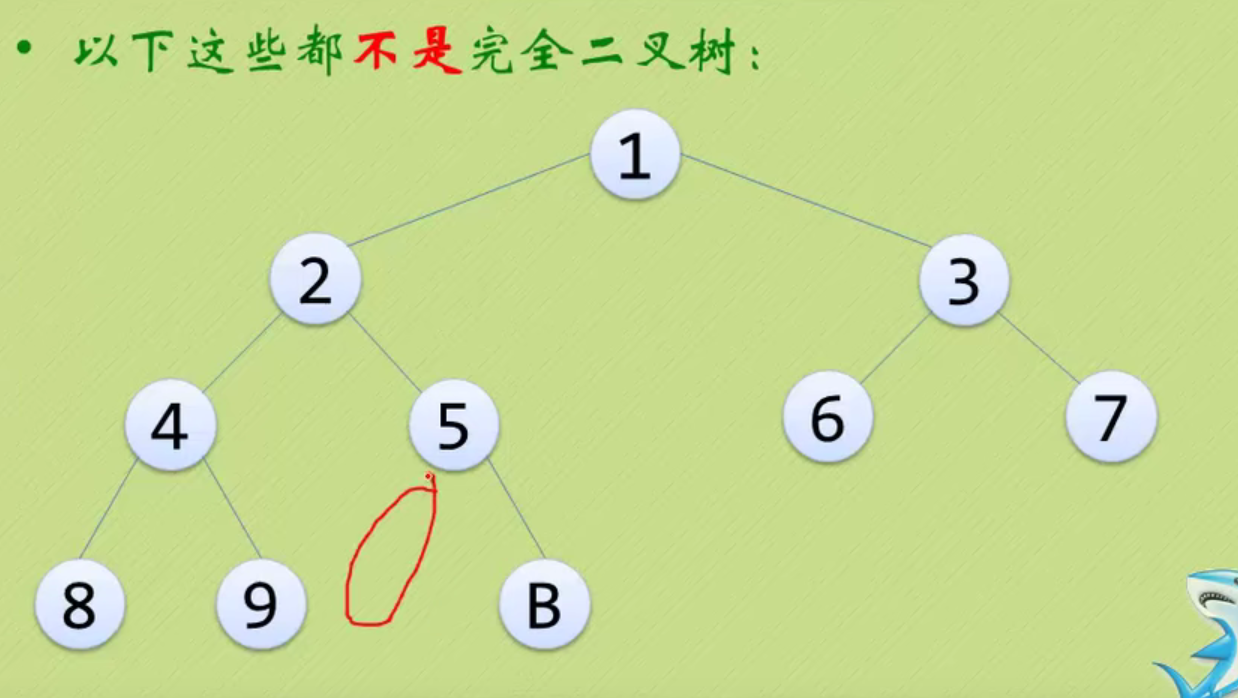
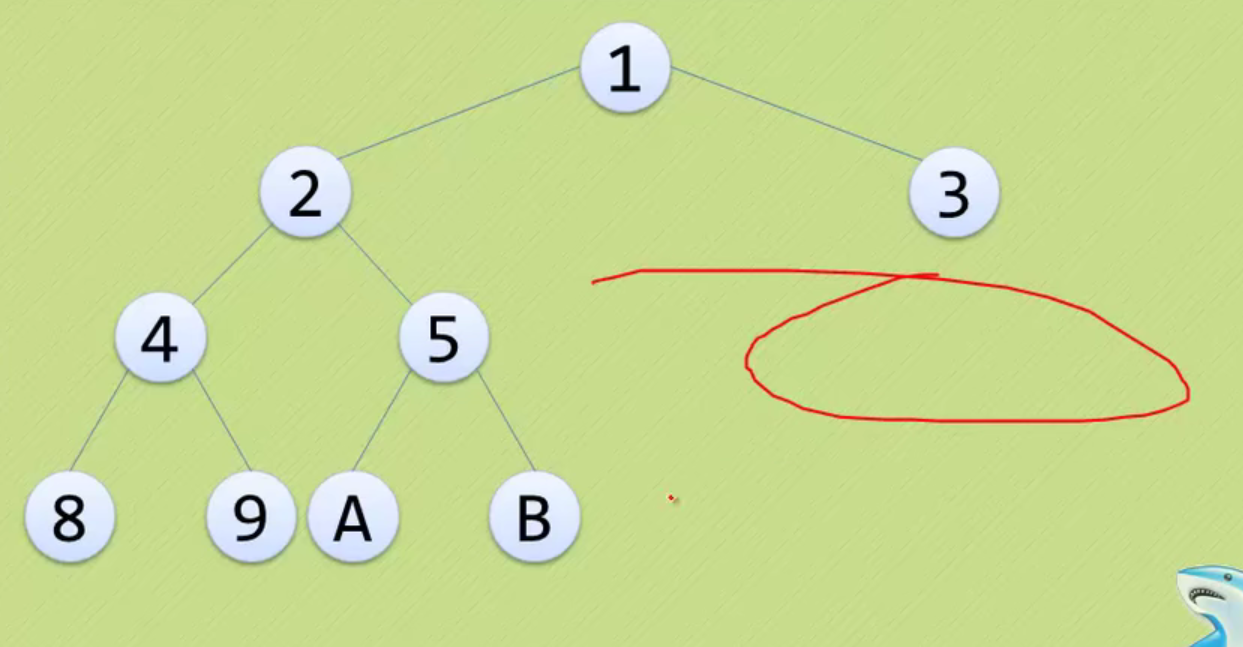
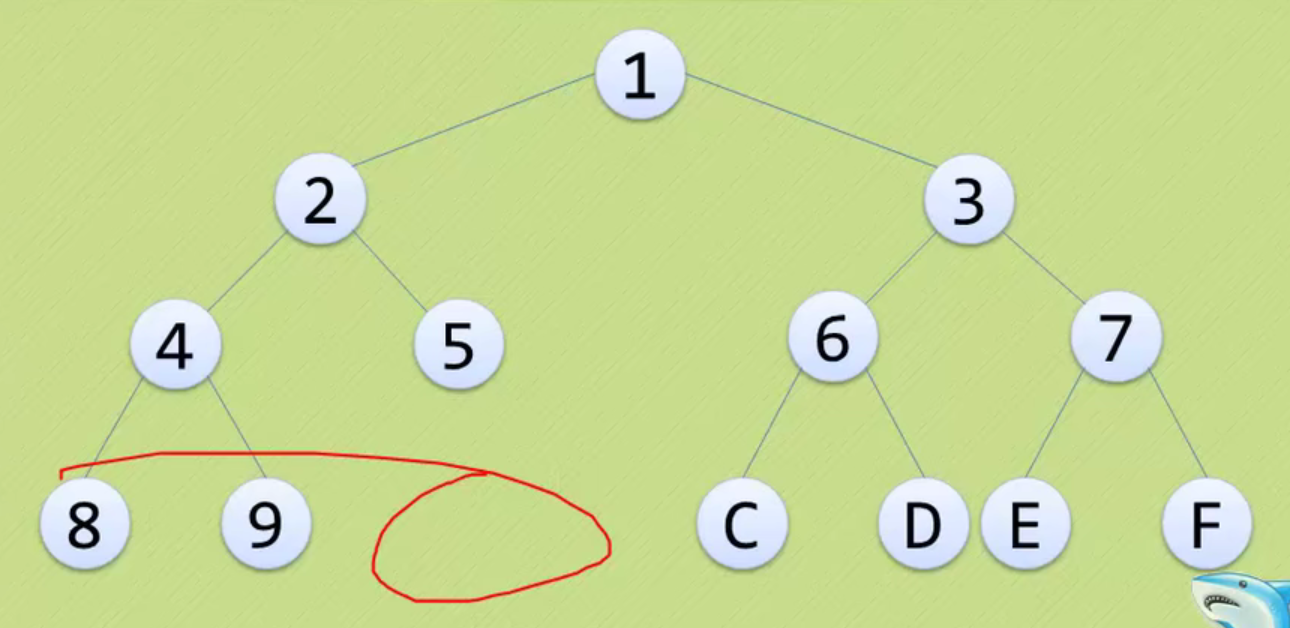
The above three are just ordinary binary trees

Properties of binary tree
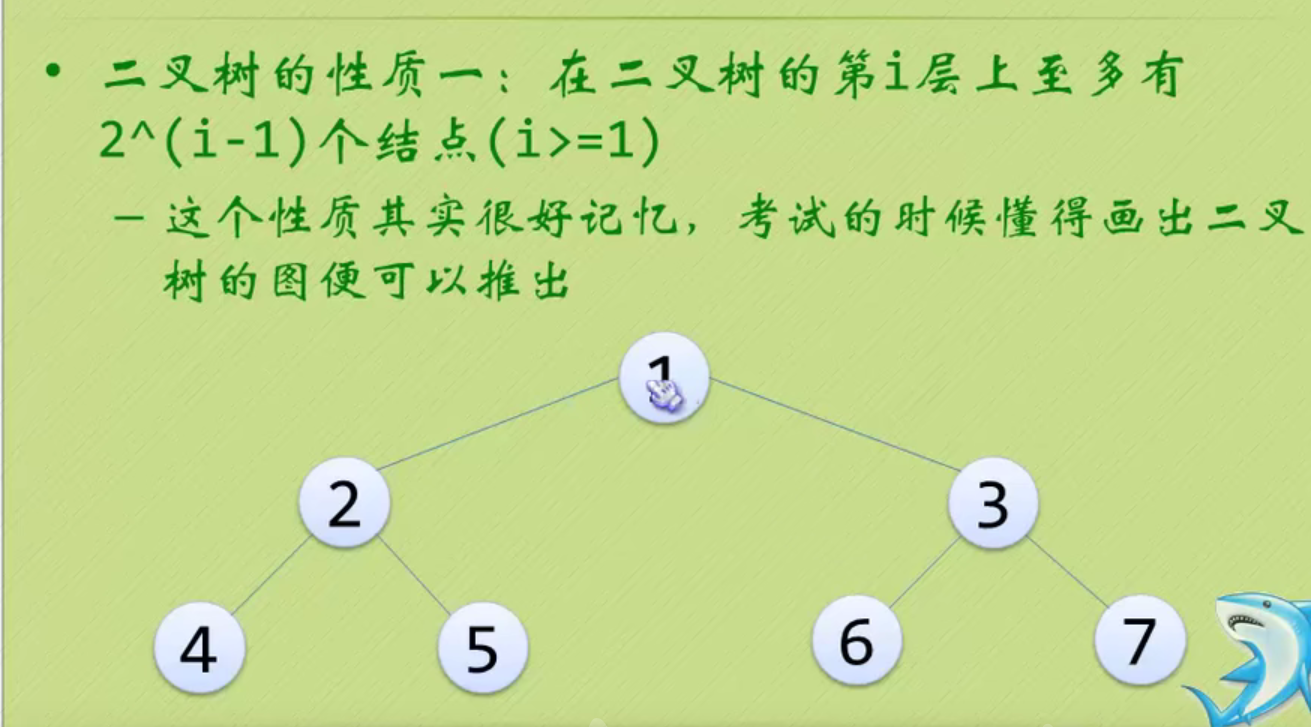
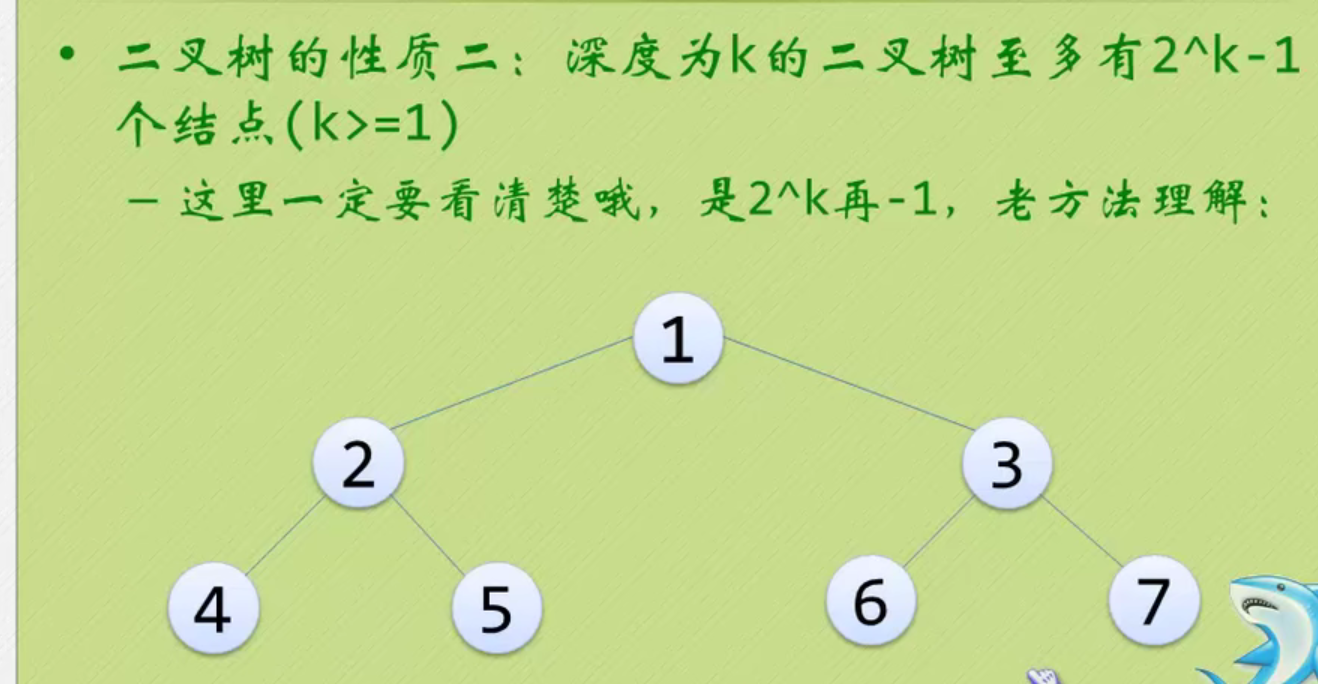


Round up and down.



It's too theoretical. Just have a look. It's not interesting.
Storage structure of binary tree

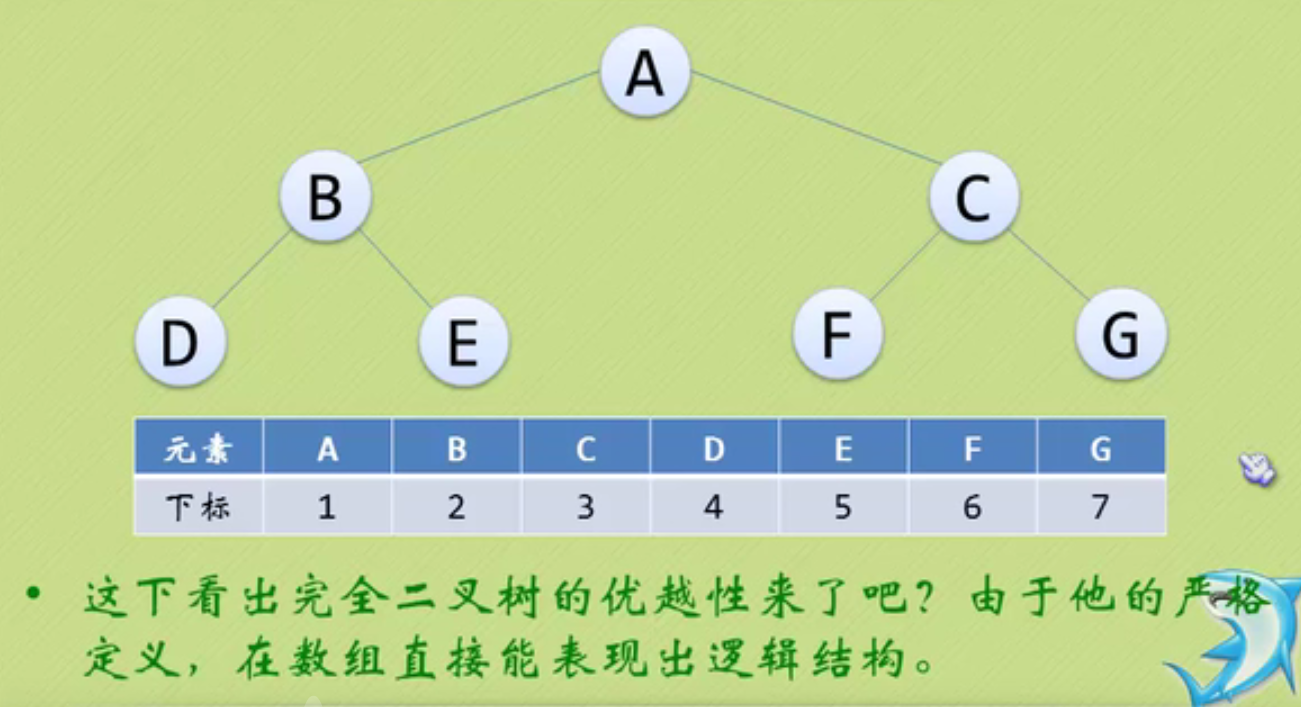
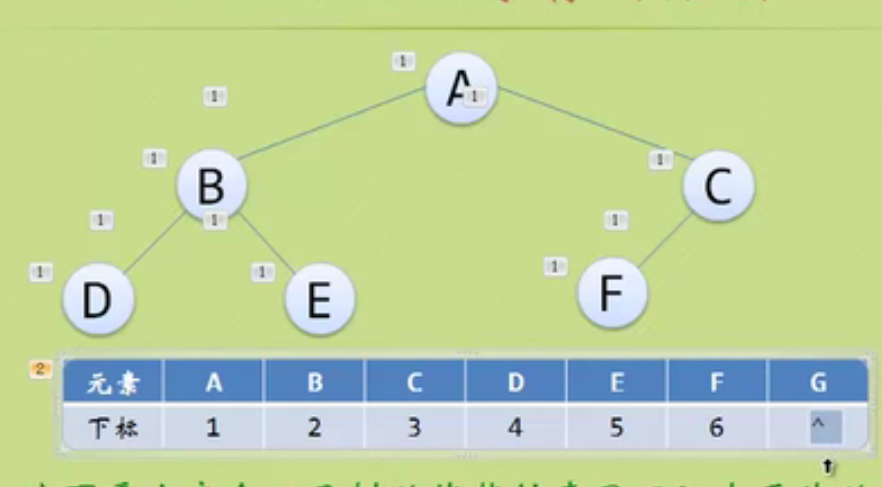
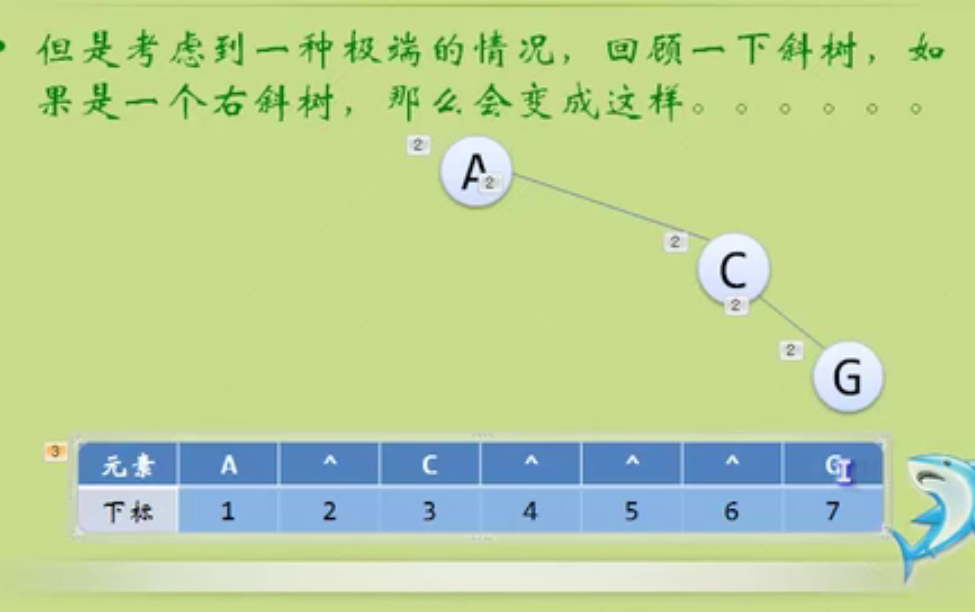
This is a waste of resources.

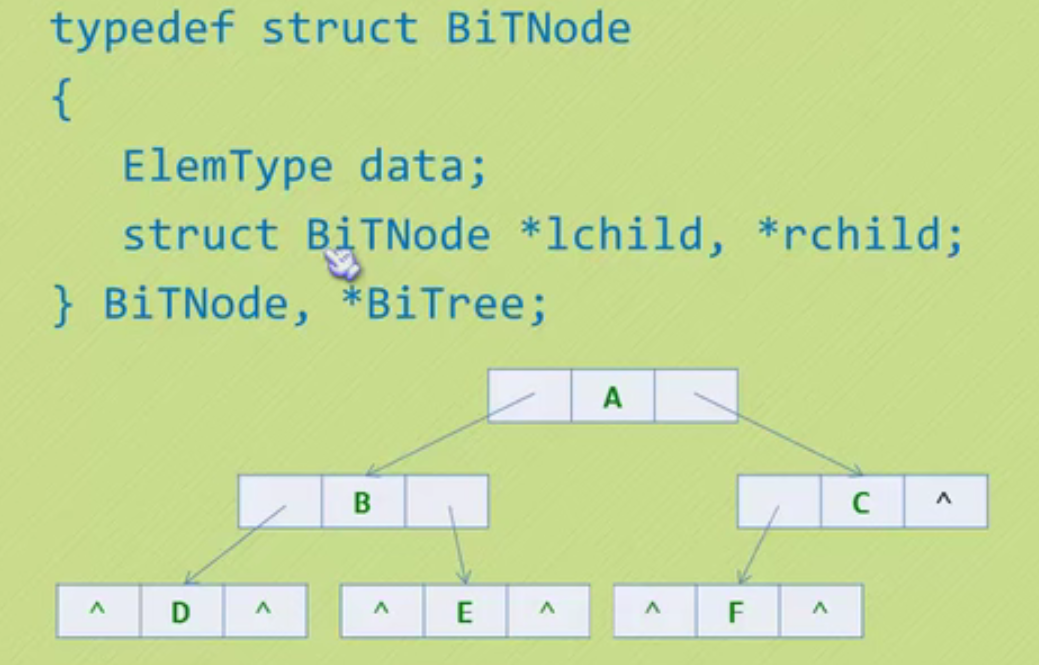
Traversal of binary tree


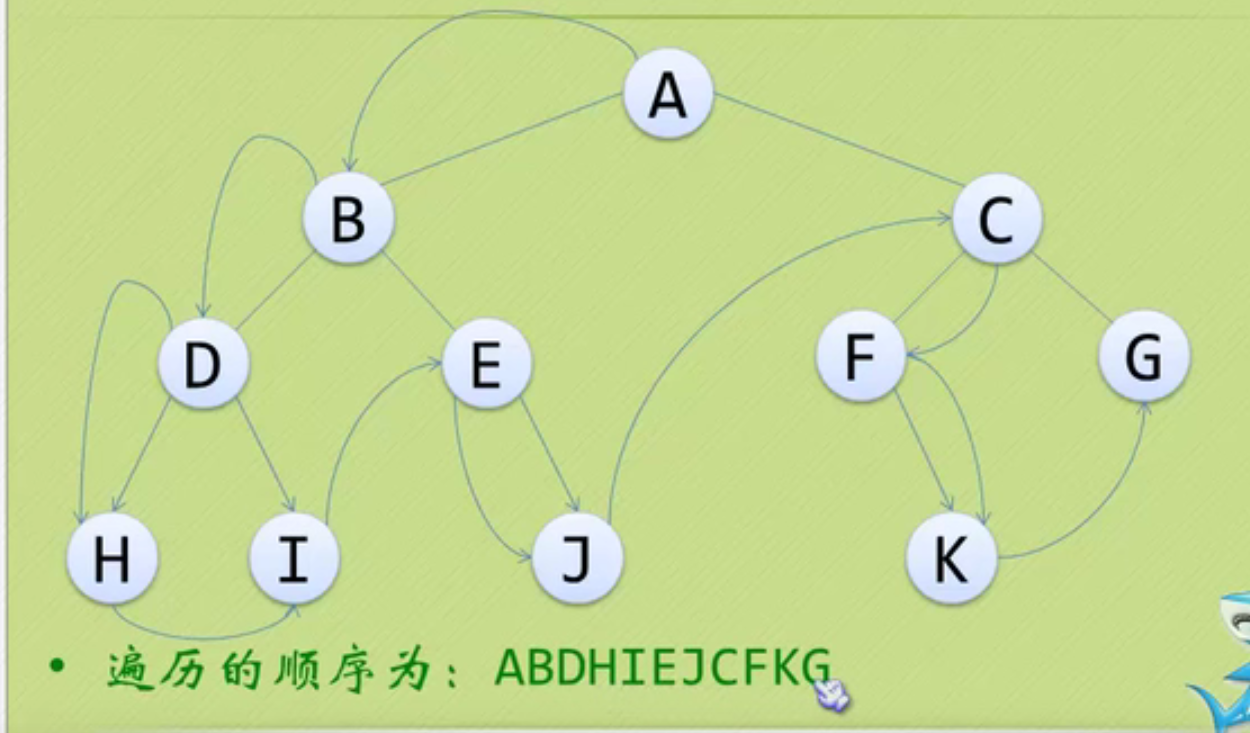

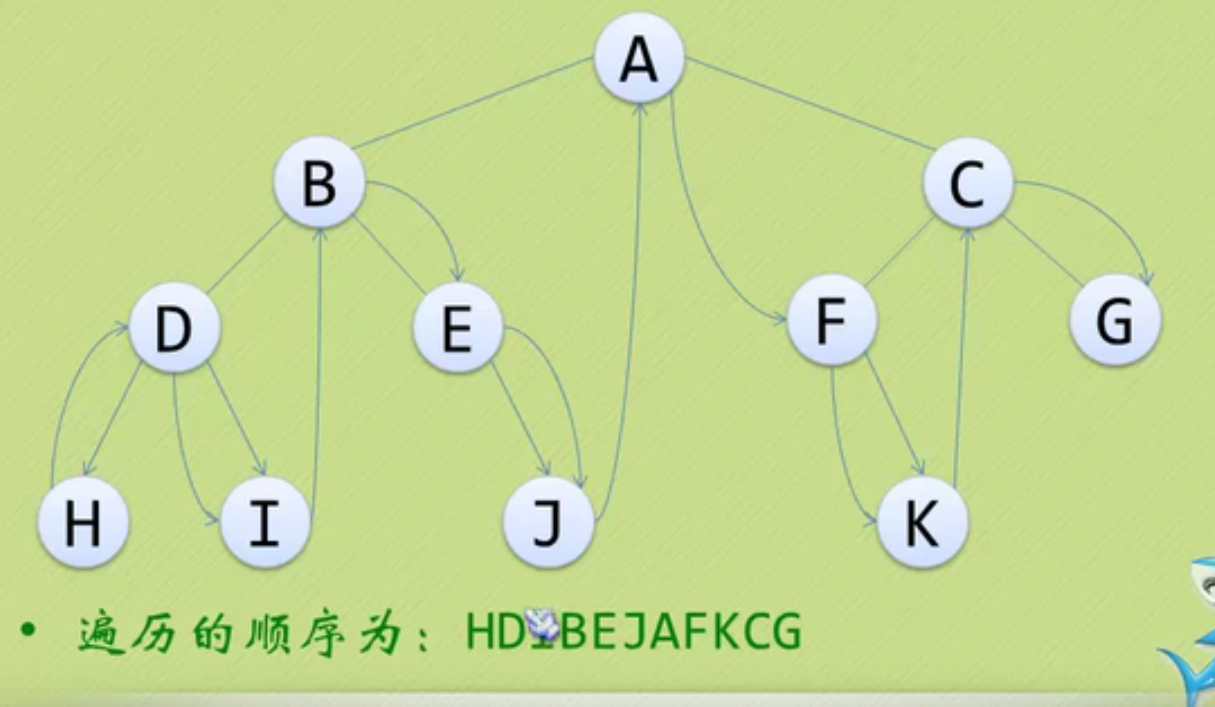

It's easy to remember the concept of big family and small family
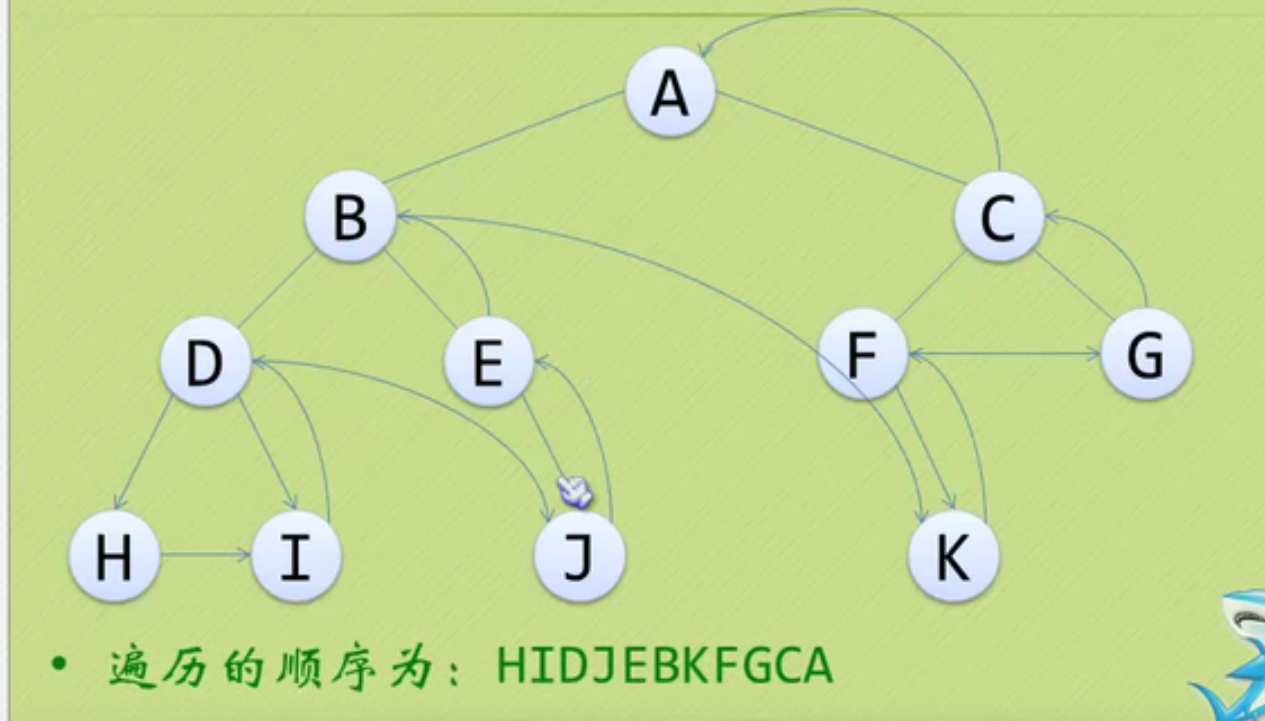

Establishment and traversal algorithm of binary tree
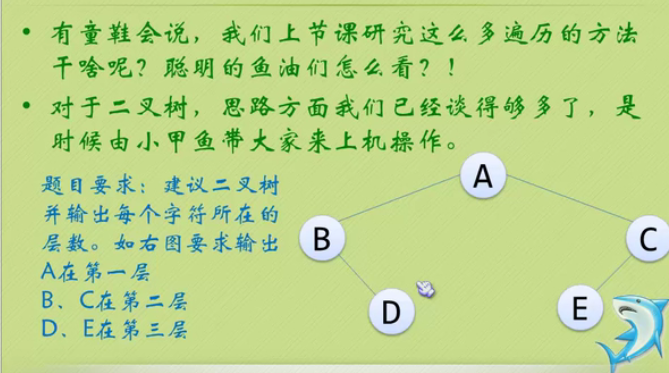
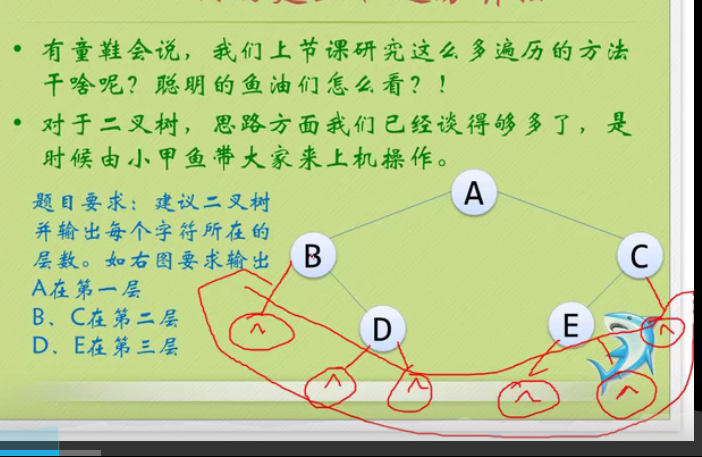
#include <iostream>
#include <stdlib.h>
#include <stdio.h>
using namespace std;
typedef char ElemType;
typedef struct BiTNode
{
char data;
struct BiTNode *lchild,*rchild;
}BiTNode ,*BiTree;
//Create a binary tree
/**
* The user enters the left and right root in the way of preorder traversal
* @param *T It's a pointer
*/
void CreatBiTree(BiTree *T)
{
char c;
scanf("%c",&c);
if(' '==c)//Develop good code writing habits
{
*T=NULL;//If the character is a space, let this point to a null pointer
}
else
{
*T= (BiTNode *)malloc(sizeof (BiTNode));//(BiTNode *) force to a pointer of type BiTNode
(*T)->data=c;
CreatBiTree(&(*T)->lchild);
CreatBiTree(&(*T)->rchild);
}
}
//Specific operations for accessing binary tree nodes
void visit(char c,int level)
{
cout<<c<<"In the first"<<level<<"layer"<<endl;
}
//Traversal binary tree
void PreOrderTraverse(BiTree T,int level)
{
if(T)
{
//If the root is traversed in middle order, just change the position
visit(T->data,level);
PreOrderTraverse(T->lchild,level+1);
PreOrderTraverse(T->rchild,level+1);
}
}
//The input method is AB space D space CE space
void test_PreTravese()
{
int level=1;
BiTree T=NULL;
CreatBiTree(&T);
PreOrderTraverse(T,level);
}
int main() {
test_PreTravese();
return 0;
}
Clue binary tree
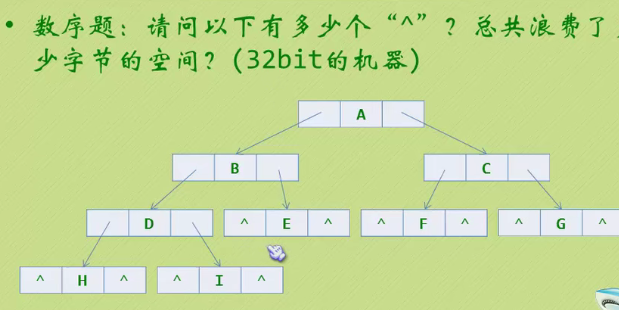
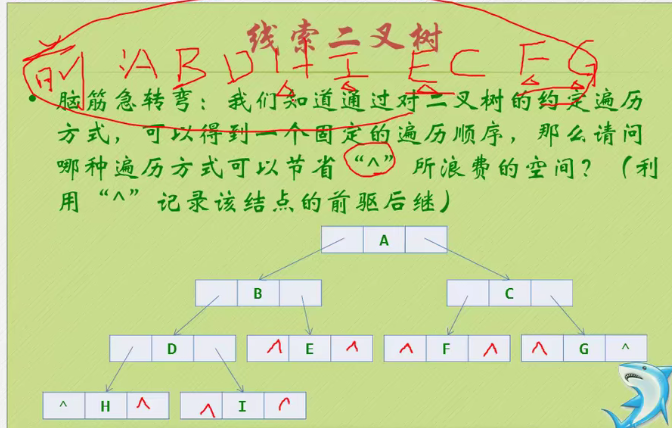
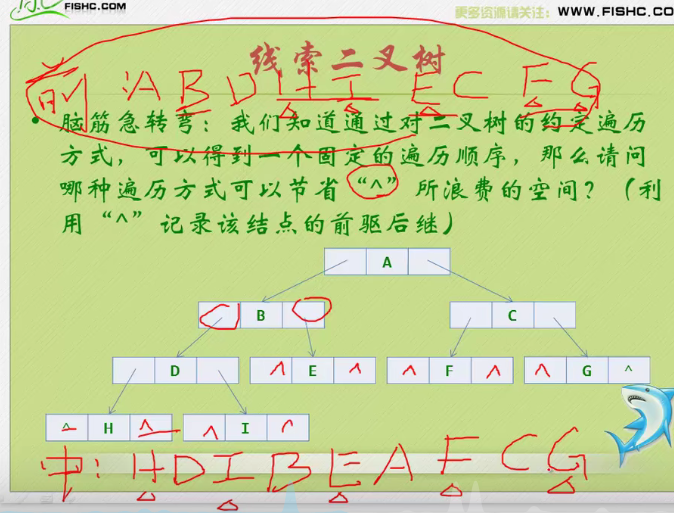
Using middle order seems to solve this problem
Because the discovery is a law separated one by one
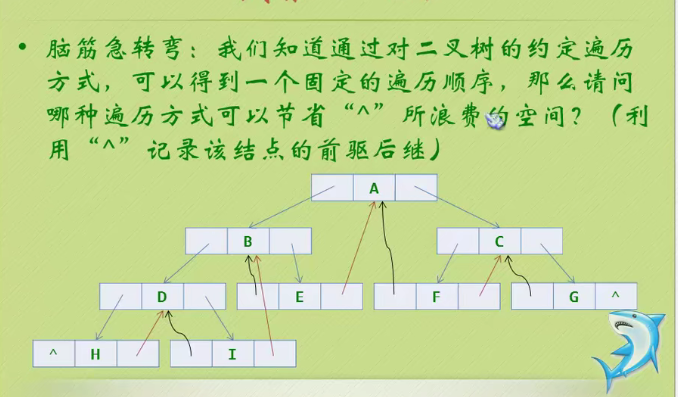
The front drive is represented by a black curved arrow
The following is indicated by a red straight arrow



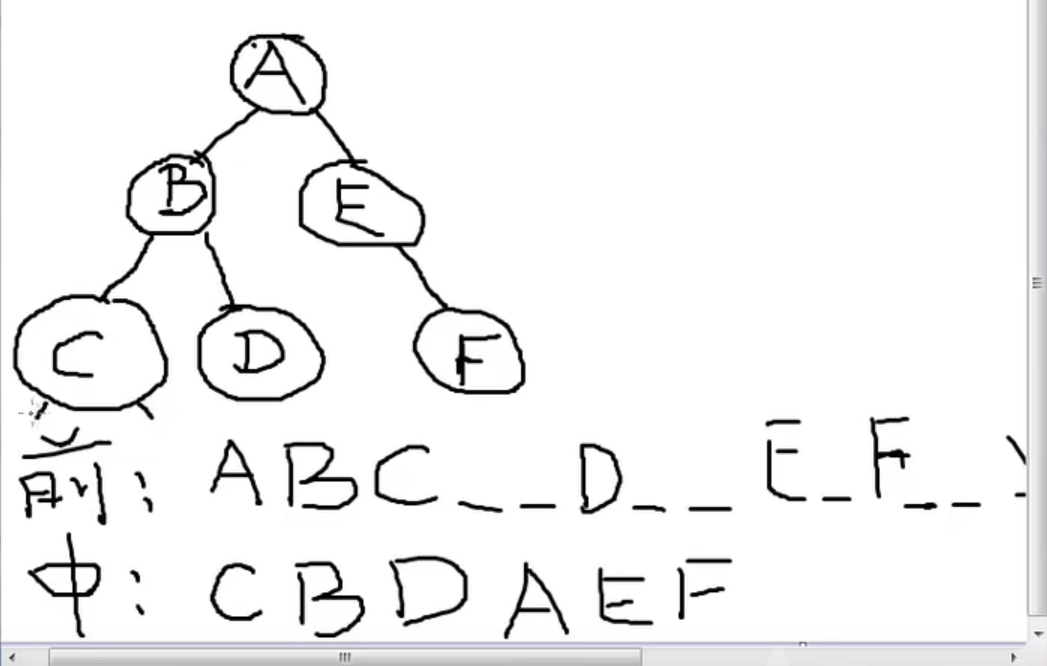
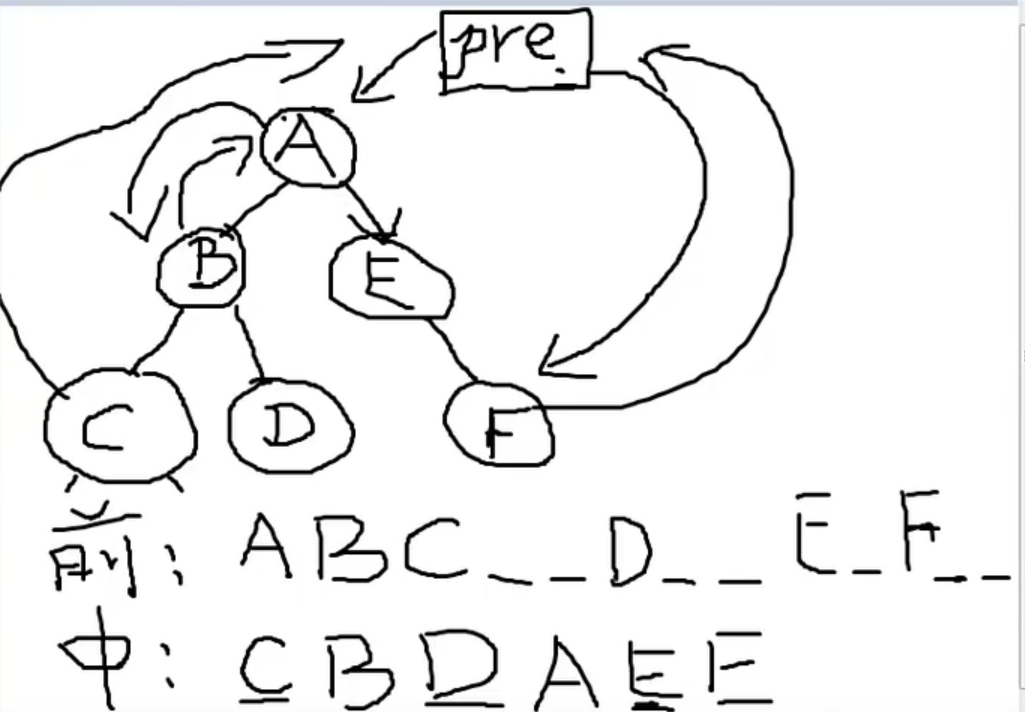
This program is difficult to understand. It is recommended to debug.
#include <iostream>
#include <stdlib.h>
#include <stdio.h>
using namespace std;
typedef char ElemType;
//Thread store flag bit enumeration
//Link(0) indicates the pointer to the left and right children
//Thread(1) indicates a clue to the predecessor and successor
typedef enum{Link,Thread} PointerTag;
typedef struct BiThrNode
{
ElemType data;
struct BiThrNode *lchild,*rchild;
PointerTag ltag;
PointerTag rtag;
}BiThrNode,*BithrTree;
//The global variable always points to the node you just accessed
BithrTree pre;
//Create a binary tree and agree that users enter data by traversing in the previous order
/**
*
* @param *T It's a pointer
*/
void CreatBiTree(BithrTree *T)
{
char c;
scanf("%c",&c);
if(' '==c)//Develop good code writing habits
{
*T=NULL;//If the character is a space, let this point to a null pointer
}
else
{
*T= (BiThrNode *)malloc(sizeof (BiThrNode));//(BiTNode *) force to a pointer of type BiTNode
(*T)->data=c;
//First set it to have left and right children
(*T)->ltag=Link;
(*T)->rtag=Link;
CreatBiTree(&(*T)->lchild);
CreatBiTree(&(*T)->rchild);
}
}
//Middle order traversal cueing
void InThreading(BithrTree T)
{
if(T)
{
InThreading(T->lchild);//Recursive left child cueing is to go to the leftmost one first, and the leftmost one will point to the following statement
//Node processing
if(!T->lchild)//If the node has no left child, set ltag to Thread and point lchild to the node just accessed
{
T->ltag=Thread;
T->lchild=pre;
}
if(!pre->rchild)
{
pre->rtag=Thread;
pre->rchild=T;
}
pre=T;
InThreading(T->rchild);//Recursive right child cueing
}
};
void visit(char c)
{
cout<<c<<endl;
}
//Middle order traversal binary tree iteration
//T here should be the header pointer pre
void InorderTravse(BithrTree T)
{
BithrTree p;
p=T->lchild;
while(p!=T)
{
while(p->ltag==Link)//Find the lowest left node
{
p=p->lchild;
}
visit(p->data);
while(p->rtag==Thread && p->rchild!=T)
{
p=p->rchild;
visit(p->data);
}
p=p->rchild;//Point back to the head node
}
}
void InorderThreading(BithrTree *p,BithrTree T)
{
*p=(BiThrNode *)malloc(sizeof (BiThrNode));
(*p)->ltag=Link;
(*p)->rtag=Thread;
(*p)->rchild=*p;
if(!T)
{
(*p)->lchild=*p;
}
else
{
(*p)->lchild=T;
pre=*p;
InThreading(T);
//After the recursion, pre points to f and performs the following actions to point the left child of C to F
pre->rchild=*p;
pre->rtag=Thread;
(*p)->rchild=pre;
}
}
int main() {
BithrTree p,T=NULL;
CreatBiTree(&T);
InorderThreading(&p,T);
cout<<"The output result of middle order traversal is:"<<endl;
InorderTravse(p);
return 0;
}
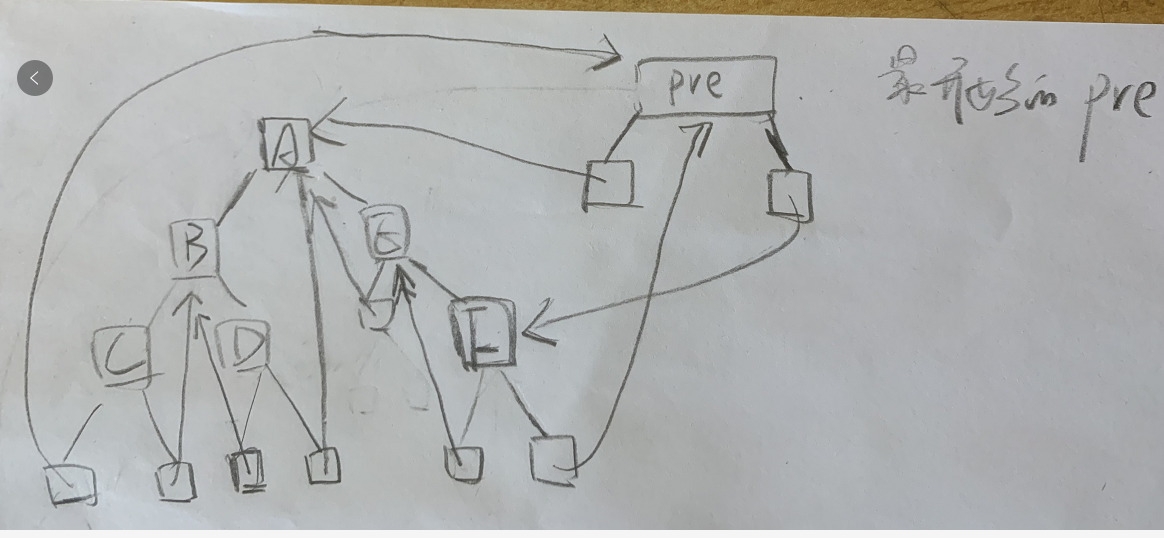
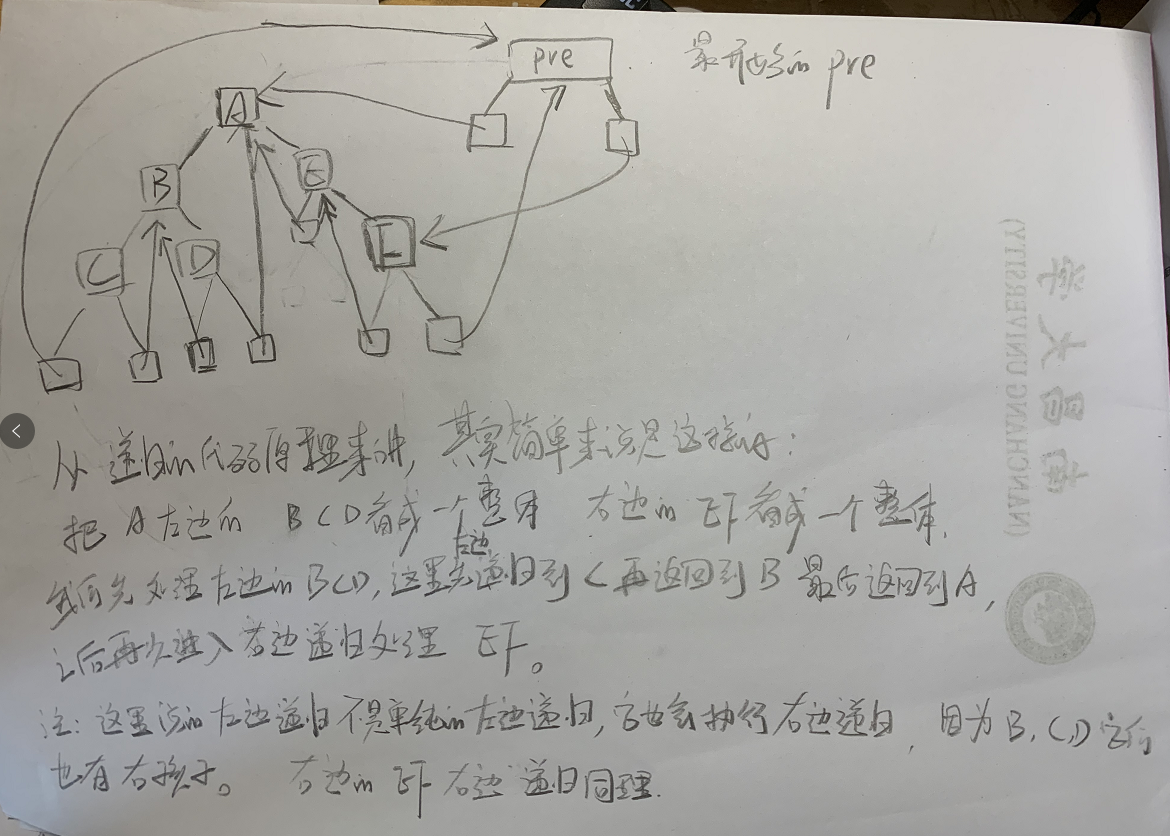
Transformation of trees, forests and binary trees
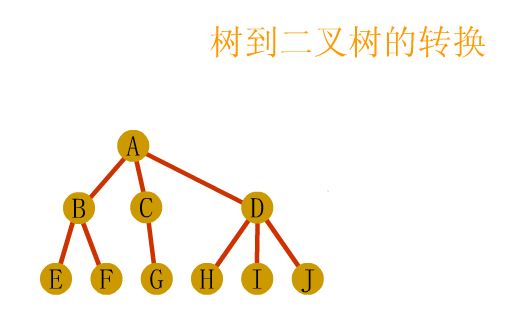
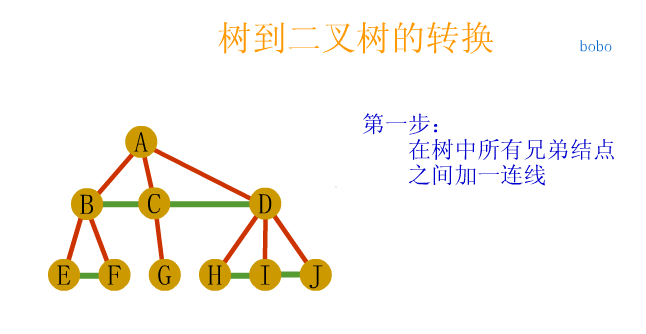
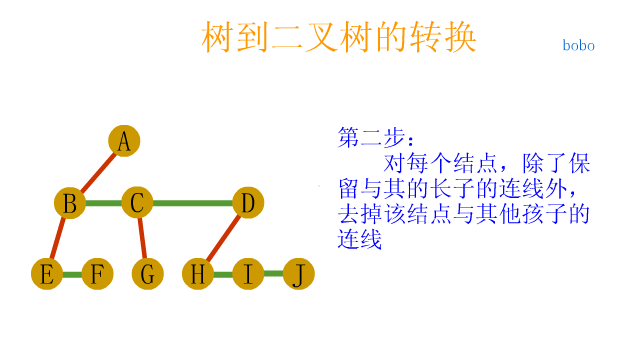
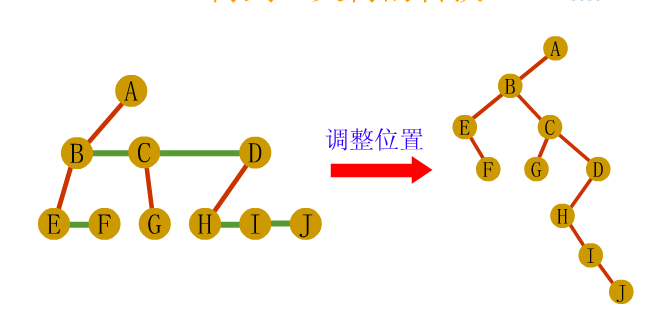

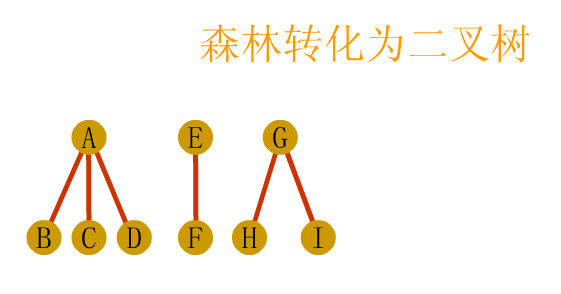
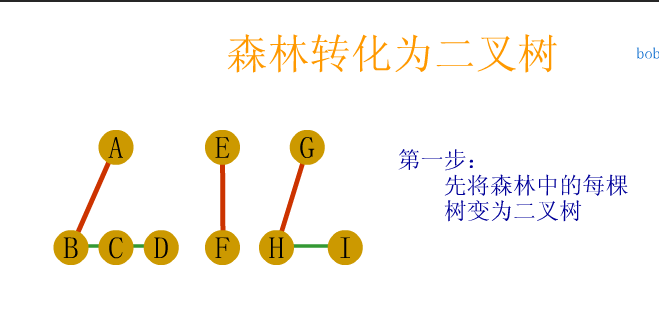
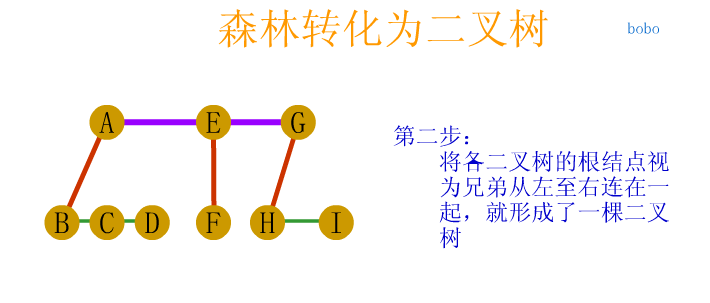
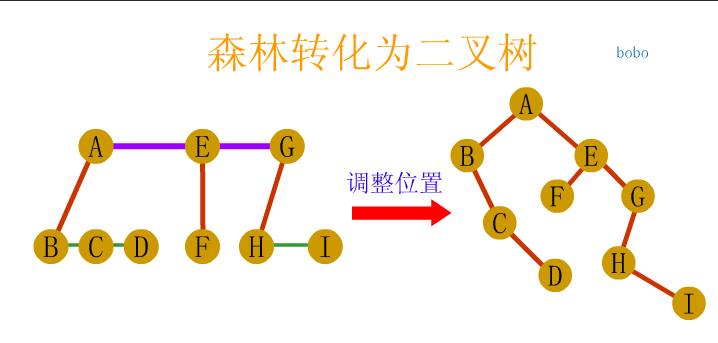

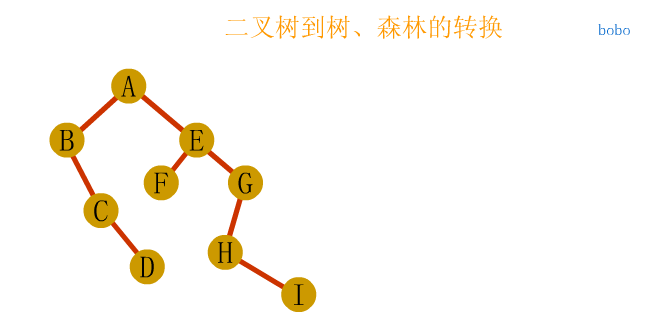
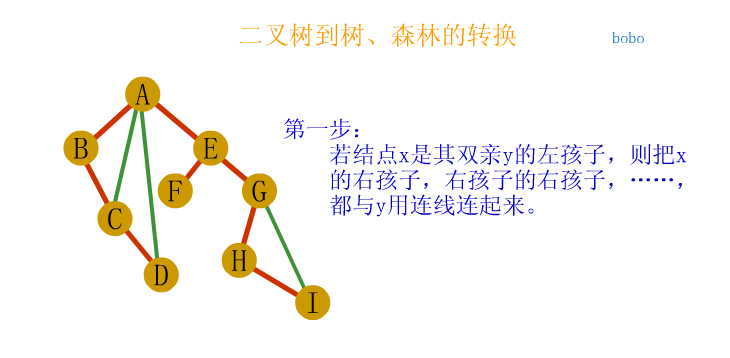
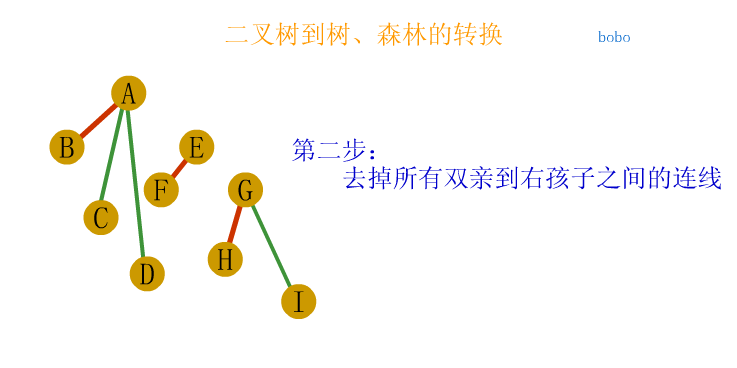
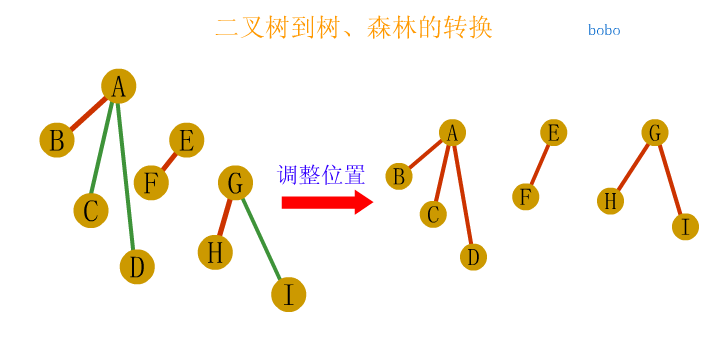

Traversal of trees and forests

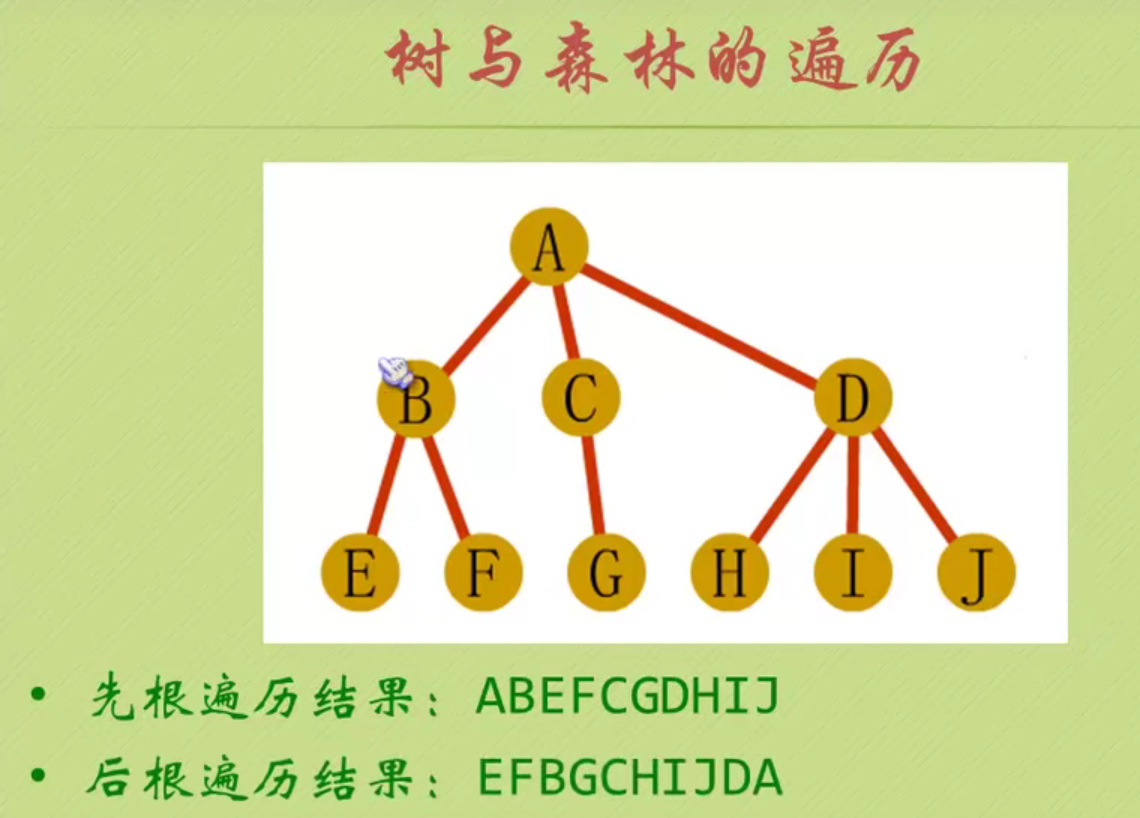

huffman tree

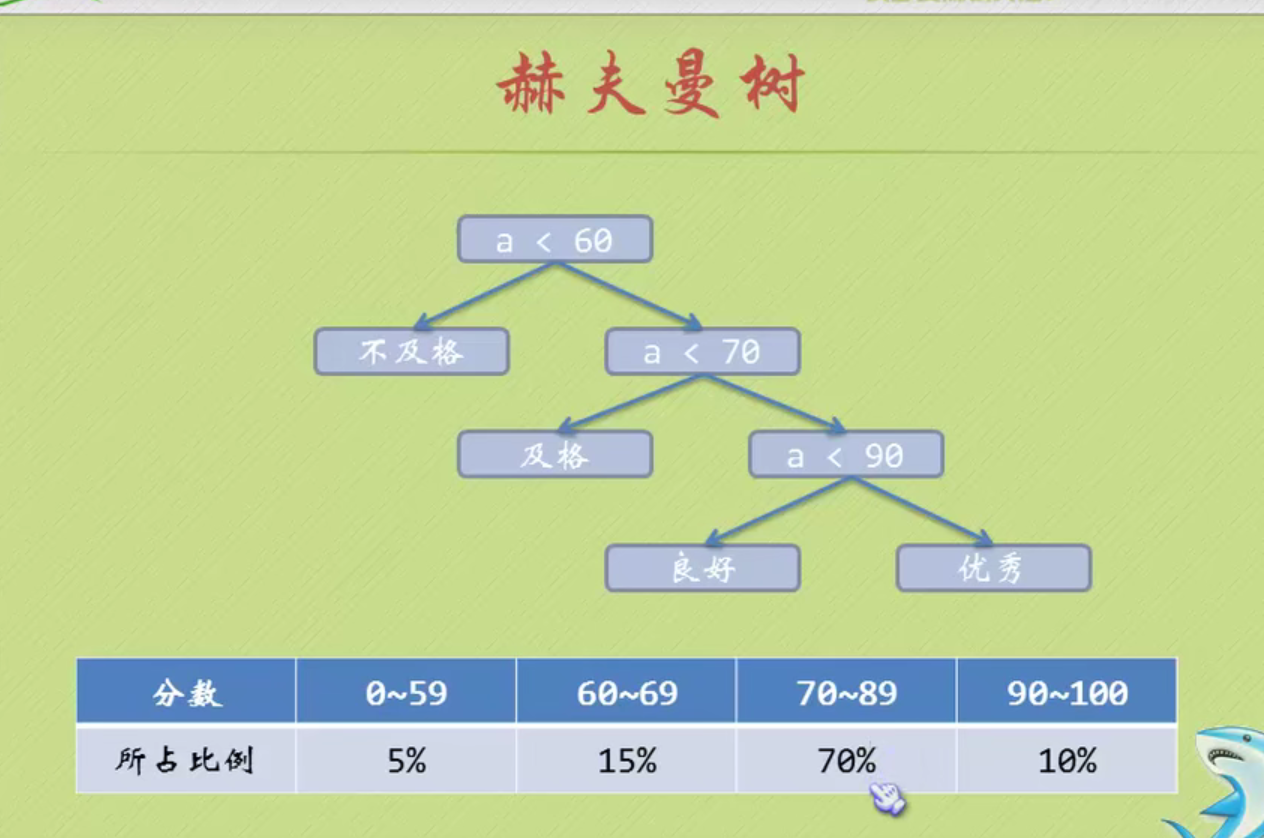
People with 70-90 scores need to make three judgments to know (this score segment accounts for the largest proportion). The efficiency is a little low
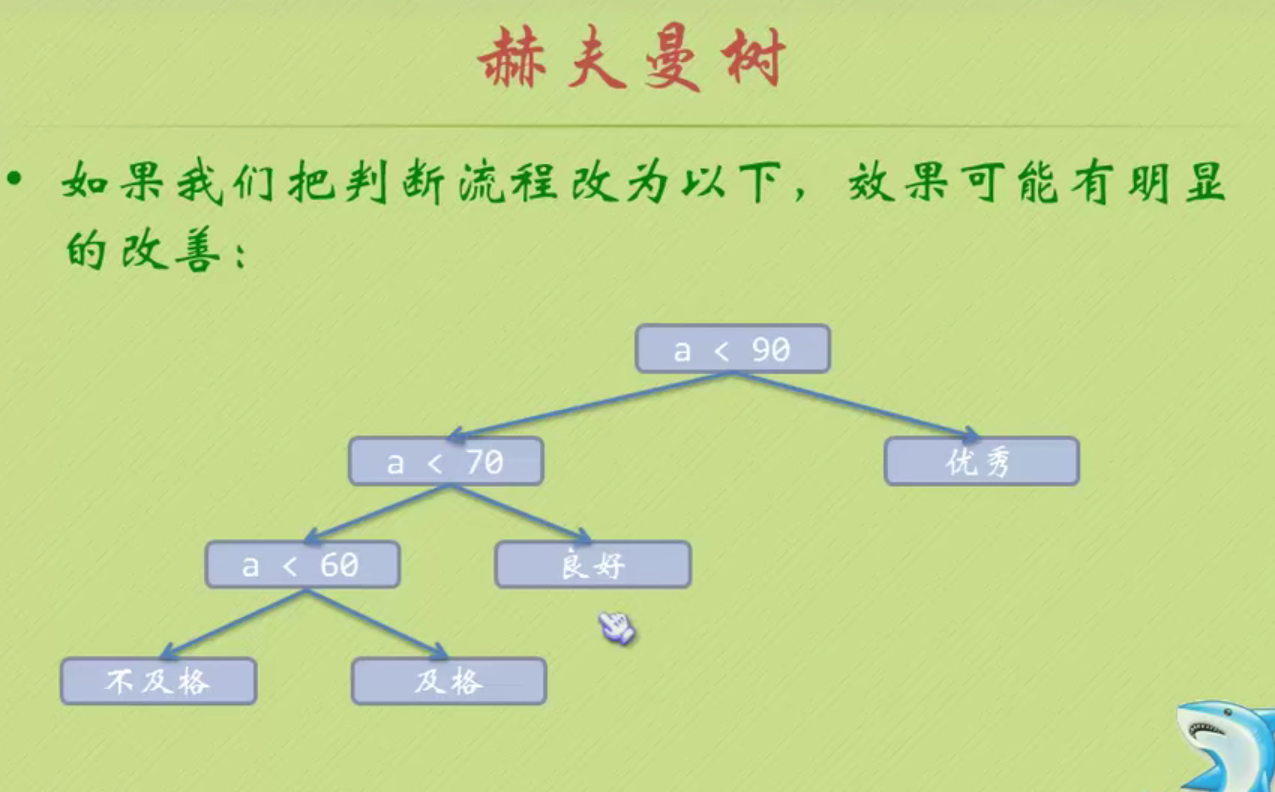
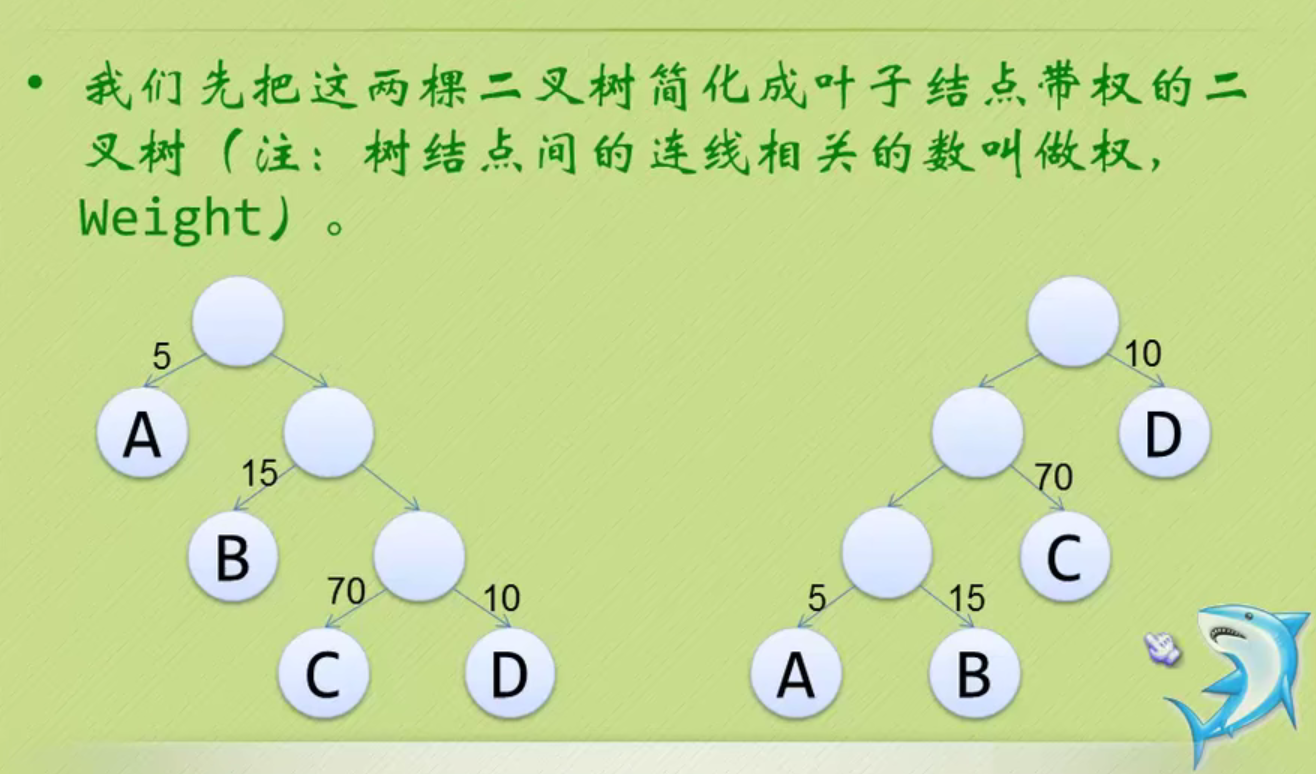

Corresponding data of the left tree To node c For example: C Path length: 3 Path length of tree: 1+2+3+3 C Weighted path length: 70*3 Weighted path length of tree WPL: 1*5+15*2+70*3+10*3 Corresponding data of the right tree Weighted path length of tree WPL: 1*10+2*70+3*15+3*5 Obviously, the weighted path length of the right tree WPL Less than the weighted path length of the left tree WPL,So the tree on the right is more efficient.

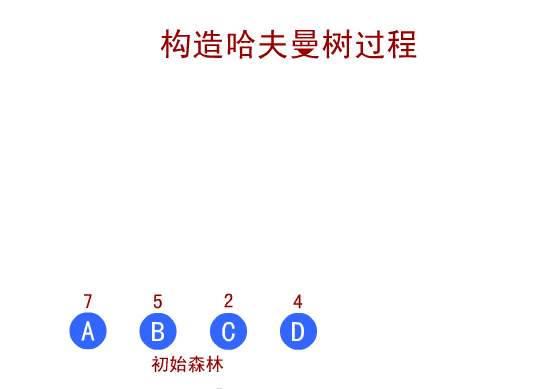
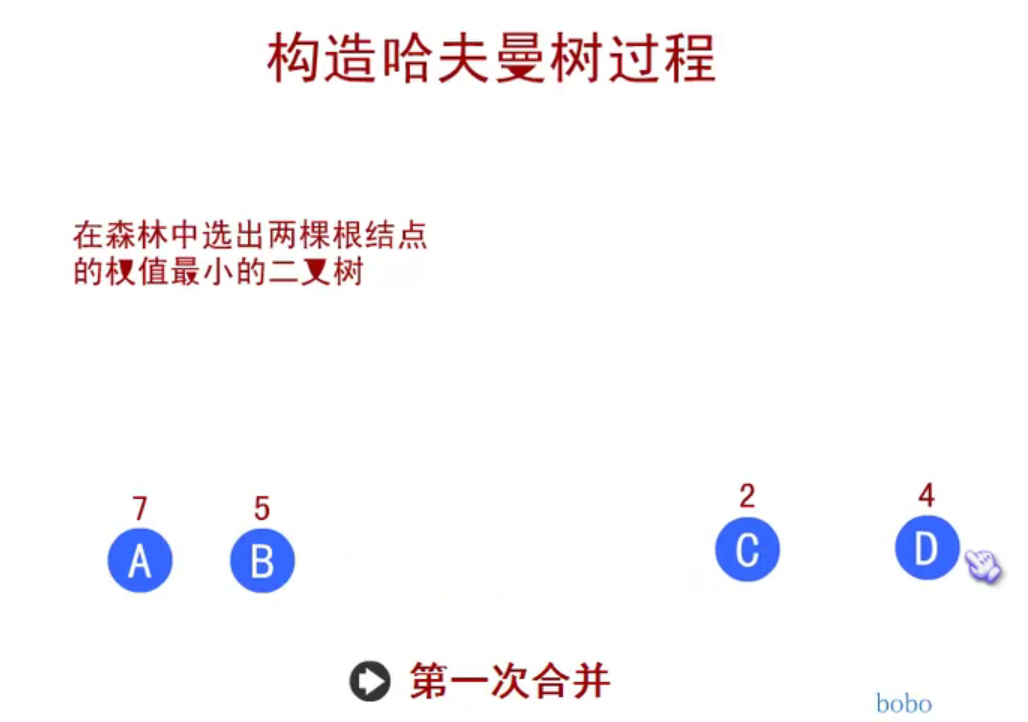
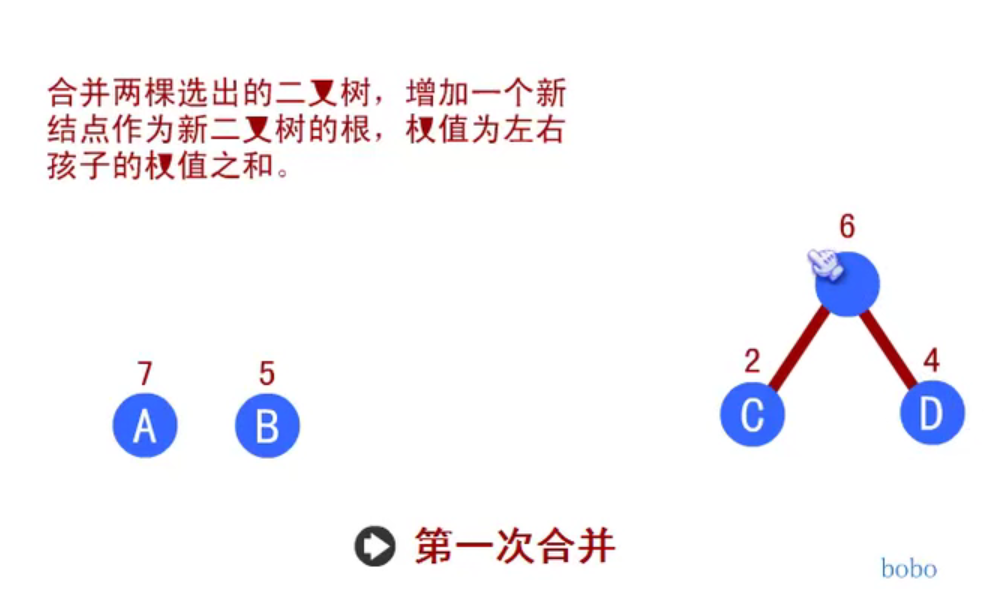
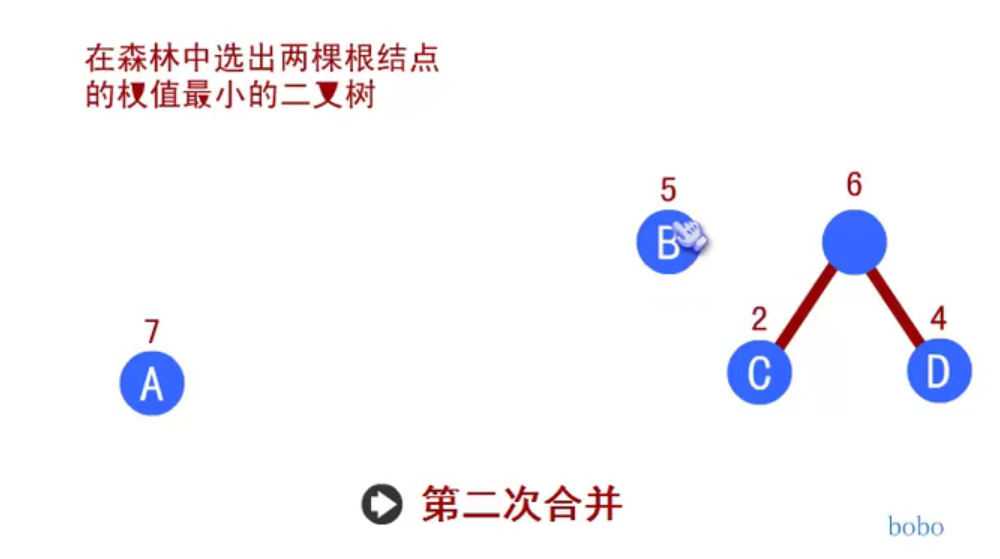
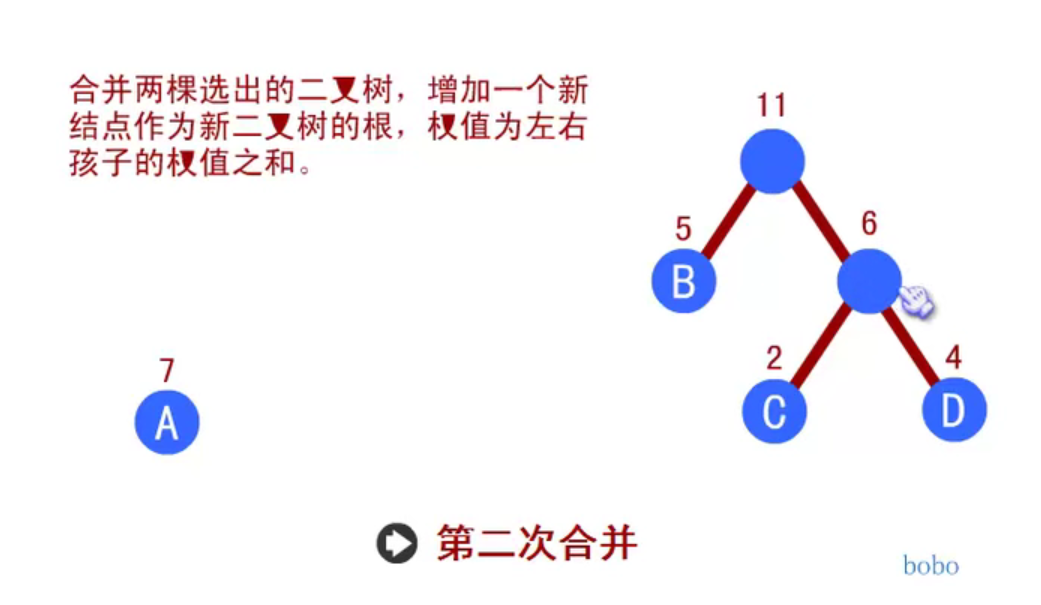
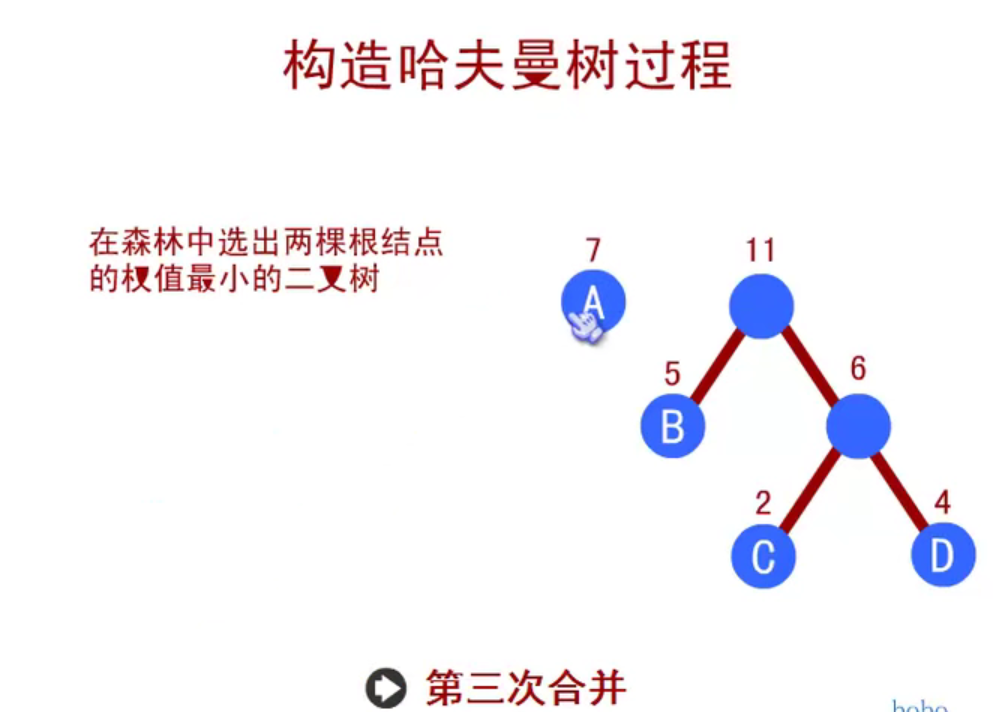
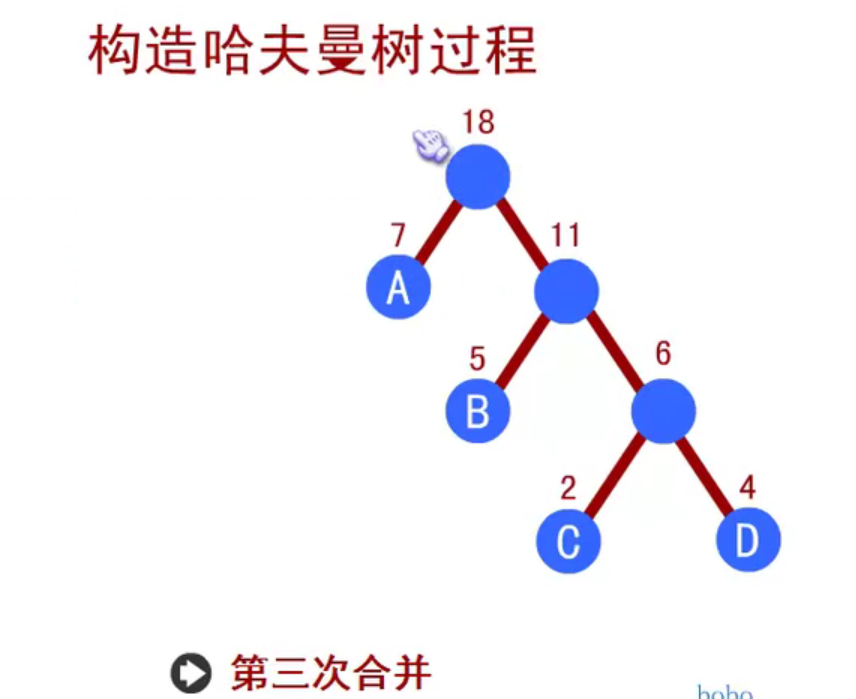
Huffman coding

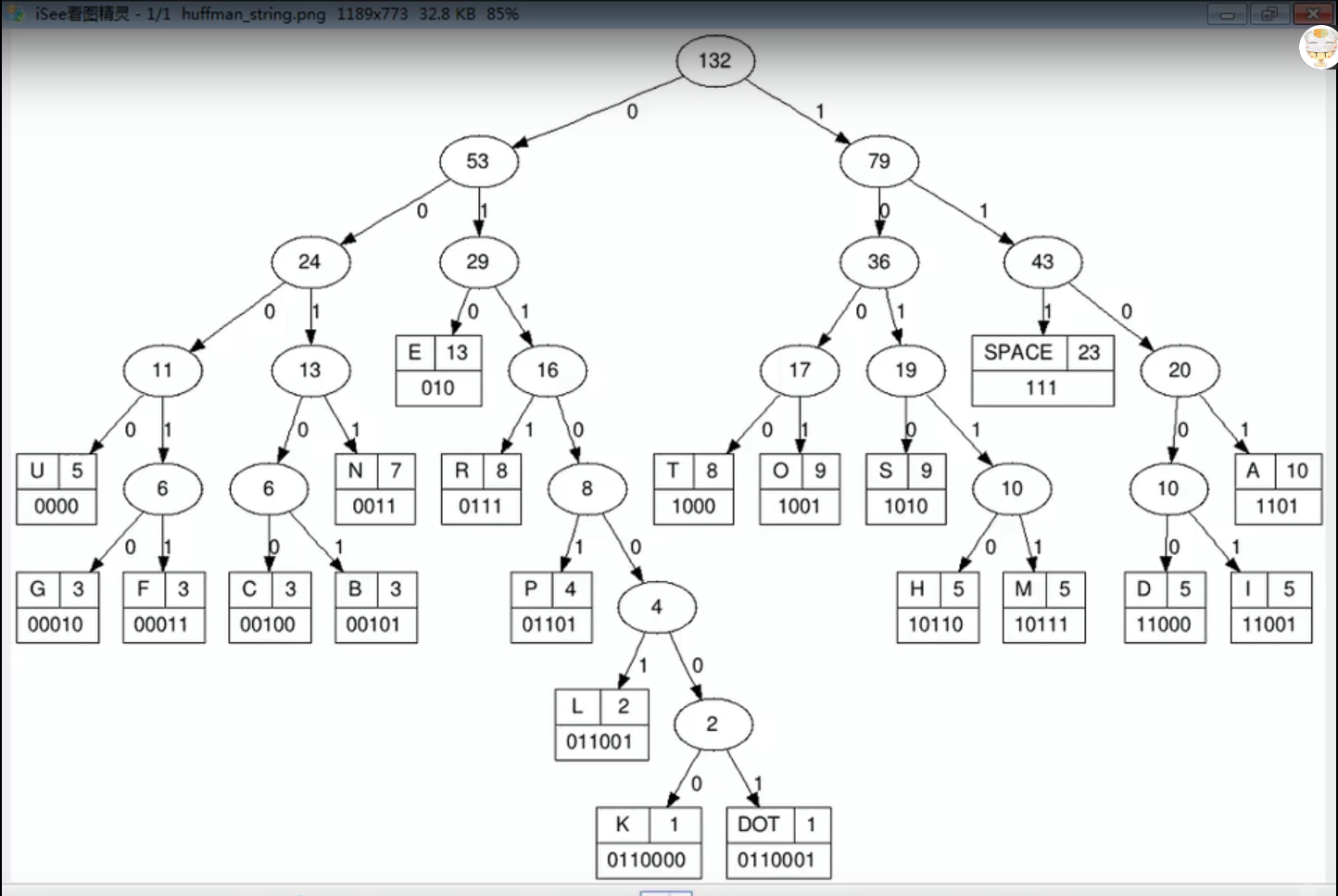


Some data structures in the code
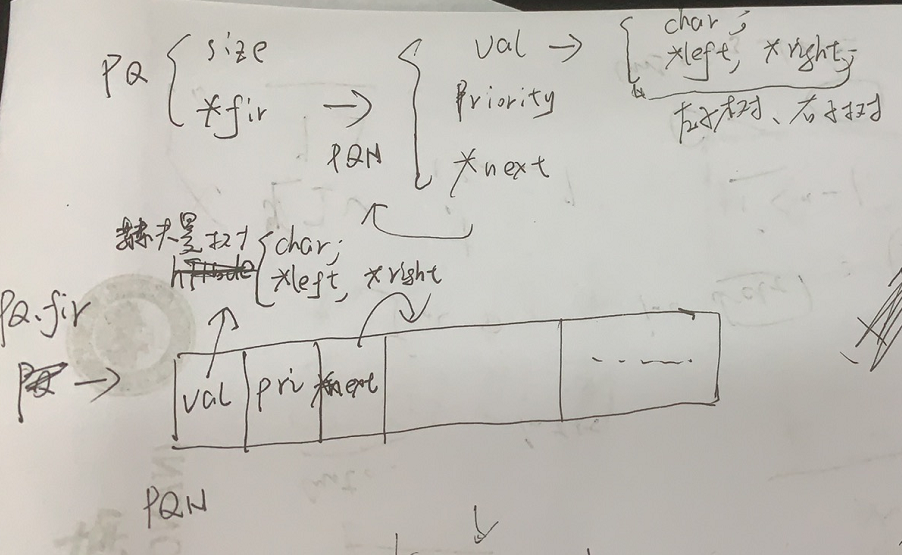
//Queue node
typedef struct _pQueueNode {
TYPE val;//Point to tree node
unsigned int priority;//The number of occurrences of characters, that is, the weight of Huffman coding
struct _pQueueNode *next;//Node pointing to the next queue
}pQueueNode;
// pQueue is the head of the queue
typedef struct _pQueue {
unsigned int size; //The length of the storage queue. The last one is the root node of the tree
pQueueNode *first; //Point to the first node of the queue
}pQueue;
//Huffman tree node
typedef struct _htNode {
char symbol;//Store character
struct _htNode *left, *right;//Left subtree right subtree
}htNode;
//The Huffman table nodes (linked list implementation)
typedef struct _hlNode {
char symbol; //Store characters such as a
char *code;//Store the Huffman code corresponding to character a, for example, 0010
struct _hlNode *next; //Point to next_ hlNode
}hlNode;
//Incapsularea listei
typedef struct _hlTable {
hlNode *first;//Point to first_ hlNode
hlNode *last;//Point to last_ hlNode
}hlTable;
The code is as follows:
pQueue.h
#pragma once / / prevent duplicate definition of header file
#ifndef _PQUEUE_H
#define _PQUEUE_H
#include "huffman.h"
//We modify the data type to hold pointers to Huffman tree nodes
#define TYPE htNode *
#define MAX_SZ 256
//Queue node
typedef struct _pQueueNode {
TYPE val;//Point to tree node
unsigned int priority;//The number of occurrences of characters, that is, the weight of Huffman coding
struct _pQueueNode *next;//Node pointing to the next queue
}pQueueNode;
// pQueue is the head of the queue
typedef struct _pQueue {
unsigned int size; //The length of the storage queue. The last one is the root node of the tree
pQueueNode *first; //Point to the first node of the queue
}pQueue;
void initPQueue(pQueue **queue);
void addPQueue(pQueue **queue, TYPE val, unsigned int priority);
TYPE getPQueue(pQueue **queue);
#endif
huffman.h
#pragma once
#ifndef _HUFFMAN_H
#define _HUFFMAN_H
//The Huffman tree node definition
//Huffman tree node
typedef struct _htNode {
char symbol;//Store character
struct _htNode *left, *right;//Left subtree right subtree
}htNode;
/*
We "encapsulate" the entire tree in a structure
because in the future we might add fields like "size"
if we need to. This way we don't have to modify the entire
source code.
*/
typedef struct _htTree {
htNode *root;
}htTree;
//The Huffman table nodes (linked list implementation)
typedef struct _hlNode {
char symbol; //Store characters such as a
char *code;//Store the Huffman code corresponding to character a, for example, 0010
struct _hlNode *next; //Point to next_ hlNode
}hlNode;
//Incapsularea listei
typedef struct _hlTable {
hlNode *first;//Point to first_ hlNode
hlNode *last;//Point to last_ hlNode
}hlTable;
htTree * buildTree(char *inputString);
hlTable * buildTable(htTree *huffmanTree);
void encode(hlTable *table, char *stringToEncode);
void decode(htTree *tree, char *stringToDecode);
#endif
pQueue.cpp
#include "pQueue.h"
#include <stdlib.h>
#include <stdio.h>
/**
* Initialize queue
* @param queue Pointer to column header
*/
void initPQueue(pQueue **queue)
{
//We allocate memory for the priority queue type
//and we initialize the values of the fields
(*queue) = (pQueue *) malloc(sizeof(pQueue));//(* queue) is equivalent to huffmanQueue generating space for the header pointer
(*queue)->first = NULL;
(*queue)->size = 0;
return;
}
/**
* Join queue
* @param queue Header pointer of the queue
* @param val Node of tree
* @param priority Number of occurrences of characters
*/
void addPQueue(pQueue **queue, TYPE val, unsigned int priority)
{
//If the queue is full we don't have to add the specified value.
//We output an error message to the console and return.
if((*queue)->size == MAX_SZ)//The queue is full
{
printf("\nQueue is full.\n");
return;
}
//The queue is not full
pQueueNode *aux = (pQueueNode *)malloc(sizeof(pQueueNode));//The node to which a queue is assigned
aux->priority = priority;//Number of character occurrences
aux->val = val;//Pointer to the node of the tree
//If the queue is empty we add the first value.
//We validate twice in case the structure was modified abnormally at runtime (rarely happens).
if((*queue)->size == 0 || (*queue)->first == NULL) //When the queue is empty, just throw things directly into it
{
aux->next = NULL;
(*queue)->first = aux;
(*queue)->size = 1;
return;
}
else//If it is not empty, it is inserted into the queue according to the law of increasing the number of characters
{
//If there are already elements in the queue and the priority of the element
//that we want to add is greater than the priority of the first element,
//we'll add it in front of the first element.
//Be careful, here we need the priorities to be in descending order
if(priority<=(*queue)->first->priority)//For example, if character a appears once and character b appears once, put the node of the queue with b in front of A
{
aux->next = (*queue)->first;//
(*queue)->first = aux;
(*queue)->size++;
return;
}
else
{
//We're looking for a place to fit the element depending on it's priority
pQueueNode * iterator = (*queue)->first;//iterator
while(iterator->next!=NULL)//Traverse the node according to the loop, so that the node is inserted into the queue according to the number of character occurrences (increasing)
{
//Same as before, descending, we place the element at the begining of the
//sequence with the same priority for efficiency even if
//it defeats the idea of a queue.
if(priority<=iterator->next->priority)
{
aux->next = iterator->next;
iterator->next = aux;
(*queue)->size++;
return;
}
iterator = iterator->next;
}
//If we reached the end and we haven't added the element,
//we'll add it at the end of the queue.
if(iterator->next == NULL)//If there is only one node in the queue and the number of characters in this node is less than that in the current node, the current node will be directly followed
{
aux->next = NULL;
iterator->next = aux;
(*queue)->size++;
return;
}
}
}
}
//Get data from the queue. The generation of Huffman tree is to obtain the priority of two tree nodes, and then add them together to generate a new tree node. The left child and the right child are the two tree nodes respectively
/**
* Obtain the corresponding tree node of the queue. After obtaining one, the first node pointed to by the queue head will move back
* @param queue Queue header pointer
* @return TYPE Pointer to tree node
*/
TYPE getPQueue(pQueue **queue)
{
TYPE returnValue;
//We get elements from the queue as long as it isn't empty
if((*queue)->size>0)
{
returnValue = (*queue)->first->val;
(*queue)->first = (*queue)->first->next;//Here, change the first node of the queue pointed to by the header pointer
(*queue)->size--;
}
else
{
//If the queue is empty we show an error message.
//The function will return whatever is in the memory at that time as returnValue.
//Or you can define an error value depeding on what you choose to store in the queue.
printf("\nQueue is empty.\n");
}
return returnValue;
}
huffman.cpp
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include "huffman.h"
#include "pQueue.h"
/**
*
* @param treeNode Throw in the node of the Huffman tree
* @param table Huffman table to be filled
* @param k Layers of Huffman tree
* @param code Huffman code --- fill in according to the rules of left subtree 0 and right subtree 1
*/
void traverseTree(htNode *treeNode, hlTable **table, int k, char code[256])
{
//If we reach the end we introduce the code in the table
if(treeNode->left == NULL && treeNode->right == NULL)//At the bottom, treeNode is a leaf
//The characters in the Huffman tree are placed on the leaves
{
code[k] = '\0';//End of string
hlNode *aux = (hlNode *)malloc(sizeof(hlNode));
aux->code = (char *)malloc(sizeof(char)*(strlen(code)+1));
strcpy(aux->code,code);
aux->symbol = treeNode->symbol;
aux->next = NULL;
//The following is a simple operation
if((*table)->first == NULL)
{
(*table)->first = aux;
(*table)->last = aux;
}
else
{
//Similar tail insertion
(*table)->last->next = aux;
(*table)->last = aux;
}
}
//We use recursion to realize traversal
//We concatenate a 0 for each step to the left
if(treeNode->left!=NULL)
{
code[k]='0';
traverseTree(treeNode->left,table,k+1,code);
}
//We concatenate a 1 for each step to the right
if(treeNode->right!=NULL)
{
code[k]='1';
traverseTree(treeNode->right,table,k+1,code);
}
}
/**
* Generate Huffman table
* @param huffmanTree
* @return
*/
hlTable * buildTable(htTree * huffmanTree)
{
//We initialize the table
hlTable *table = (hlTable *)malloc(sizeof(hlTable));
table->first = NULL;
table->last = NULL;
//Auxiliary variables
char code[256];
//k will memories the level on which the traversal is
int k=0;
//We traverse the tree and calculate the codes
traverseTree(huffmanTree->root,&table,k,code);//The nodes passed into the Huffman tree and the table to be filled,
// k stands for the layer,
// Code to store the code. If you leave the left subtree, add '0' and if you leave the right subtree, add '1'‘
return table;
}
/**
* Generating Huffman tree
* @param inputString---character string
* @return Root node of Huffman tree
*/
htTree * buildTree(char *inputString)
{
//The array in which we calculate the frequency of the symbols
//Knowing that there are only 256 posibilities of combining 8 bits
//(256 ASCII characters)
int * probability = (int *)malloc(sizeof(int)*256);
//initialization
//We initialize the array
for(int i=0; i<256; i++)
probability[i]=0;
//Count the number of occurrences of each character of the string to be encoded
//We consider the symbol as an array index and we calculate how many times each symbol appears
for(int i=0; inputString[i]!='\0'; i++)
probability[(unsigned char) inputString[i]]++;//For example, if the first character is I and its ASCII is 73, this is probability[73] + +;
//The queue which will hold the tree nodes
//pQueue queue header node
pQueue * huffmanQueue;
initPQueue(&huffmanQueue);//Initialization--
//Fill queue
//We create nodes for each symbol in the string
for(int i=0; i<256; i++)
if(probability[i]!=0)//This character has appeared
{
htNode *aux = (htNode *)malloc(sizeof(htNode));//Assign a tree node
aux->left = NULL;
aux->right = NULL;
aux->symbol = (char) i;//i represents the ASCII value of the character, (char) i becomes the corresponding character and passes this character to the tree node
addPQueue(&huffmanQueue,aux,probability[i]);//Join this queue
}
//We free the array because we don't need it anymore
free(probability);//When the probability runs out, the heap space is released
//Generating Huffman tree
//We apply the steps described in the article to build the tree
while(huffmanQueue->size!=1)//Equal to 1 means that only the root node is left
{
int priority = huffmanQueue->first->priority;
priority+=huffmanQueue->first->next->priority;//Add up the number of occurrences of the first two characters, that is, the number of new nodes, where the number is actually the weight of Huffman coding
htNode *left = getPQueue(&huffmanQueue);//After the left subtree is obtained once each time, the header pointer automatically points to the next queue node to be obtained
htNode *right = getPQueue(&huffmanQueue);//Right subtree
//Generate a new tree node
htNode *newNode = (htNode *)malloc(sizeof(htNode));
newNode->left = left;
newNode->right = right;
addPQueue(&huffmanQueue,newNode,priority);//According to the law of increasing times, check the new tree node into the queue
}
//Establish the root node of Huffman tree
//We create the tree
htTree *tree = (htTree *) malloc(sizeof(htTree));
//At this point, getpqueue (& huffmanqueue) gets the last node in the column and assigns it to the Huffman tree root node of the tree
tree->root = getPQueue(&huffmanQueue);
return tree;
}
/**
* code
* Output the Huffman encoding of the Input string
* @param table Huffman table
* @param stringToEncode The string you want to encode -- Input -- the file to be compressed
*/
void encode(hlTable *table, char *stringToEncode)
{
hlNode *traversal;//Traversal Huffman table
printf("\nEncoding\nInput string : %s\nEncoded string : \n",stringToEncode);
//For each element of the string traverse the table
//and once we find the symbol we output the code for it
for(int i=0; stringToEncode[i]!='\0'; i++)
{
traversal = table->first;
while(traversal->symbol != stringToEncode[i])//while is used to find the Huffman table node of the corresponding character
traversal = traversal->next;
printf("%s",traversal->code);
}
printf("\n");
}
/**
* decode
* In fact, it is to traverse the Huffman tree. 0 is to go to the left and 1 is to the right
* @param tree huffman tree
* @param stringToDecode Huffman code to be decoded - Input
*/
void decode(htTree *tree, char *stringToDecode)
{
htNode *traversal = tree->root;//First point to the root node of Huffman tree
printf("\nDecoding\nInput string : %s\nDecoded string : \n",stringToDecode);
//For each "bit" of the string to decode
//we take a step to the left for 0
//or ont to the right for 1
for(int i=0; stringToDecode[i]!='\0'; i++)
{
if(traversal->left == NULL && traversal->right == NULL)//I got the leaves
{
printf("%c",traversal->symbol);//Output character
traversal = tree->root;//Back to the root node
}
if(stringToDecode[i] == '0')
traversal = traversal->left;
if(stringToDecode[i] == '1')
traversal = traversal->right;
if(stringToDecode[i]!='0'&&stringToDecode[i]!='1')
{
printf("The input string is not coded correctly!\n");
return;
}
}
//The Huffman code to be decoded has been traversed here
if(traversal->left == NULL && traversal->right == NULL)
{
printf("%c",traversal->symbol);//Output character
traversal = tree->root;//Back to the root node
}
printf("\n");
}
main.cpp
#include <stdio.h>
#include <stdlib.h>
#include "huffman.h"
int main(void)
{
//We build the tree depending on the string
htTree *codeTree = buildTree("beep boop beer!");//build Huffman tree
//We build the table depending on the Huffman tree
hlTable *codeTable = buildTable(codeTree);//Huffman table, which stores the encoding of each character
//We encode using the Huffman table
encode(codeTable,"beep boop beer!");//code
//We decode using the Huffman tree
//We can decode string that only use symbols from the initial string
decode(codeTree,"0011111000111");//decode
//Output : 0011 1110 1011 0001 0010 1010 1100 1111 1000 1001
return 0;
}
chart
Many to many relationship

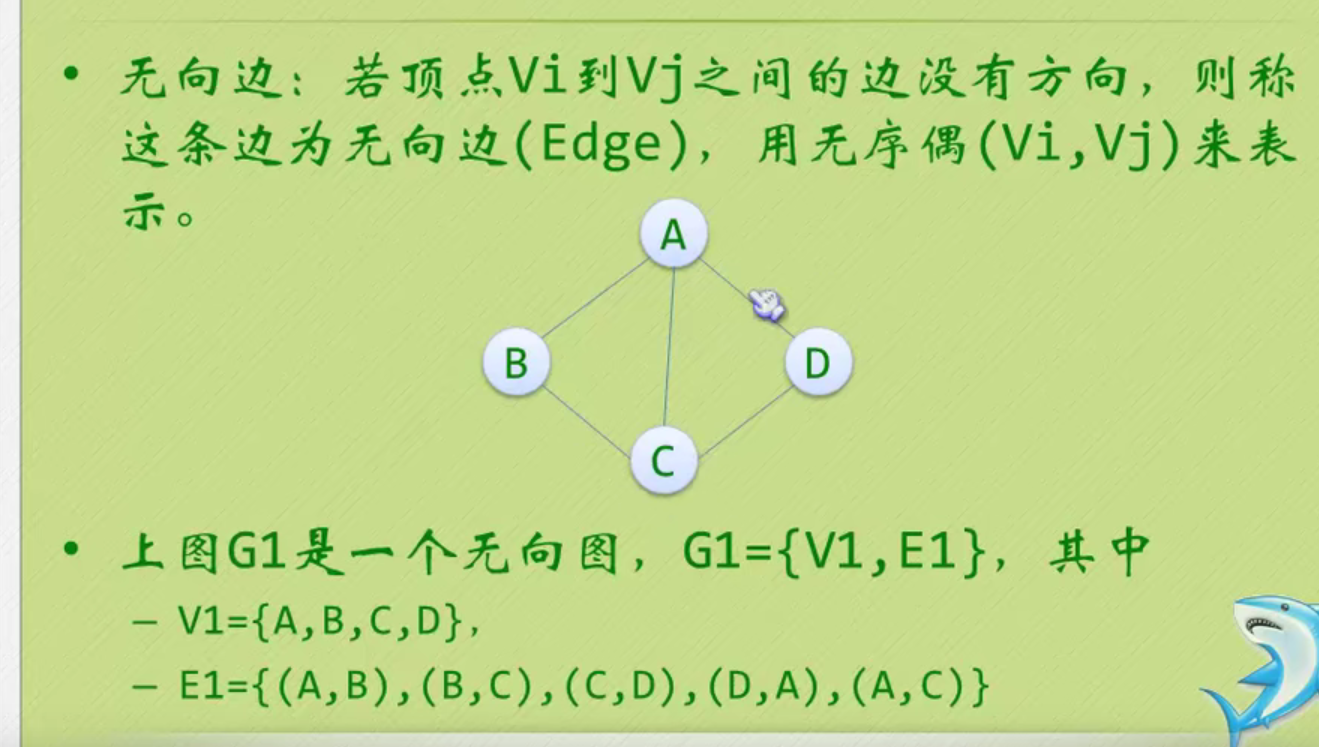
The order of vi vj in disordered pairs
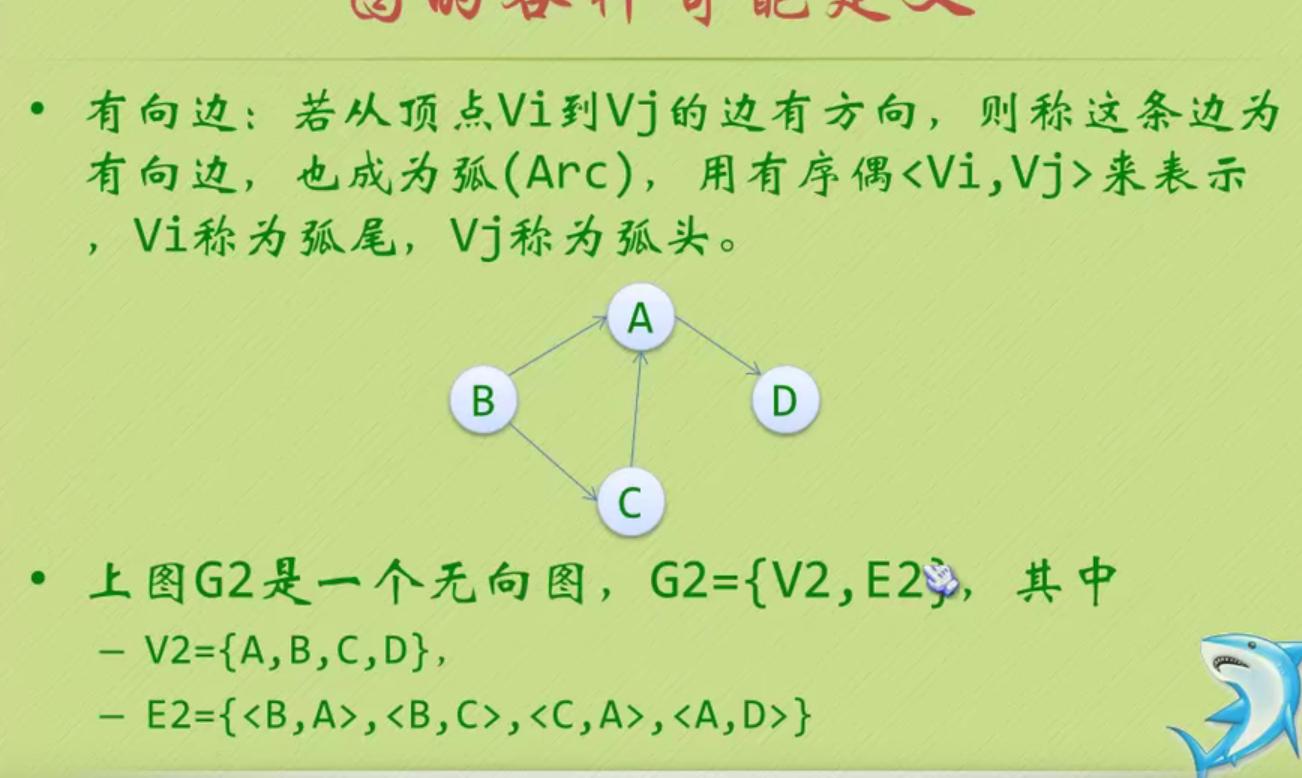
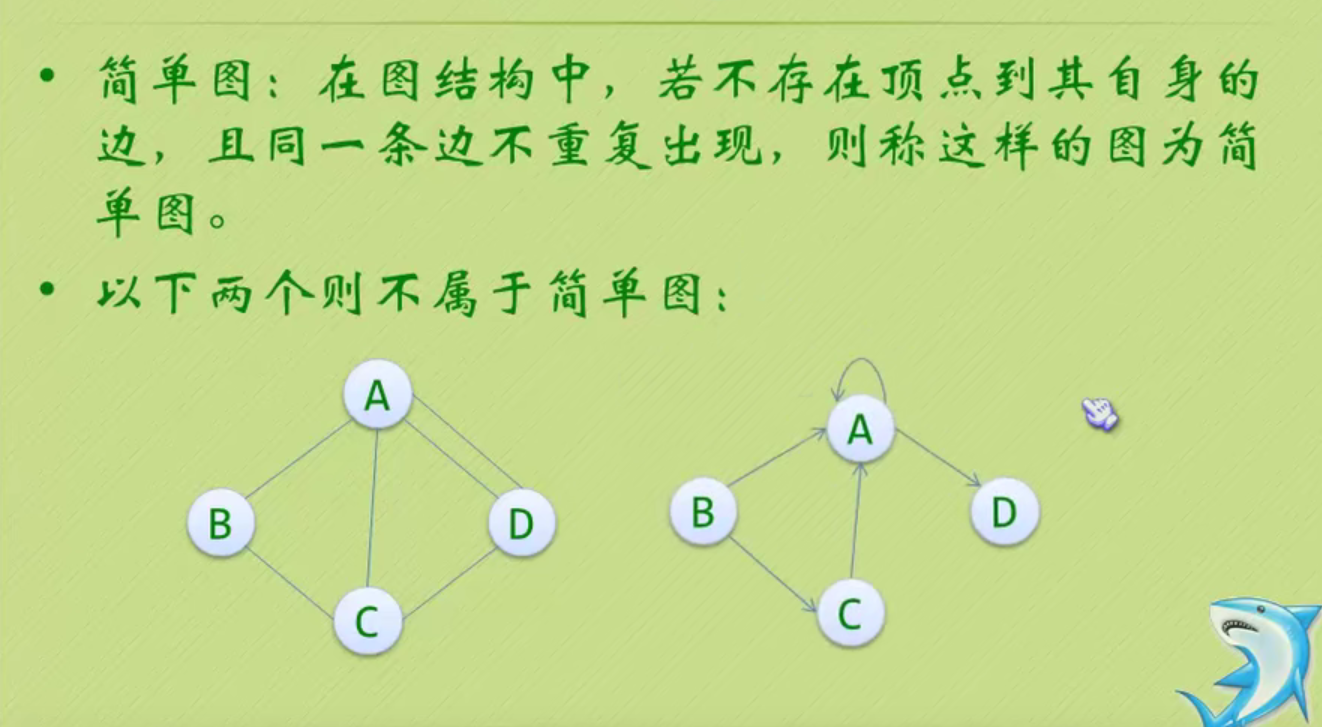
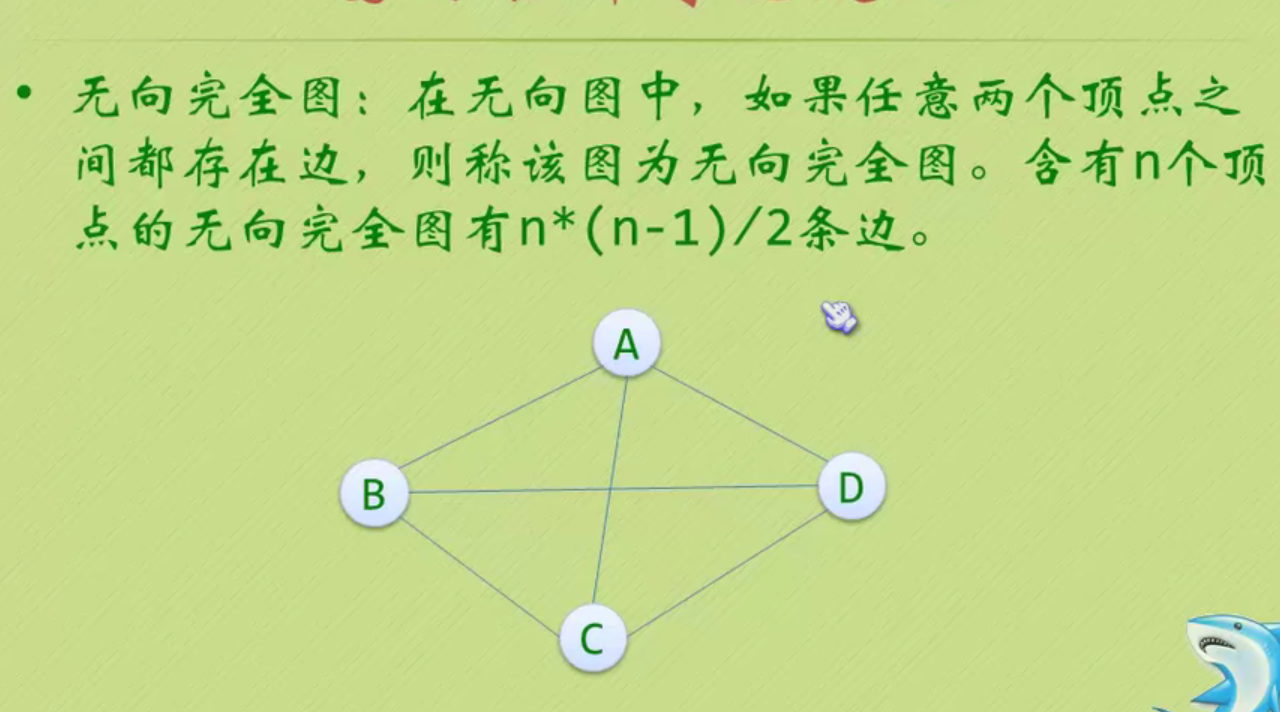
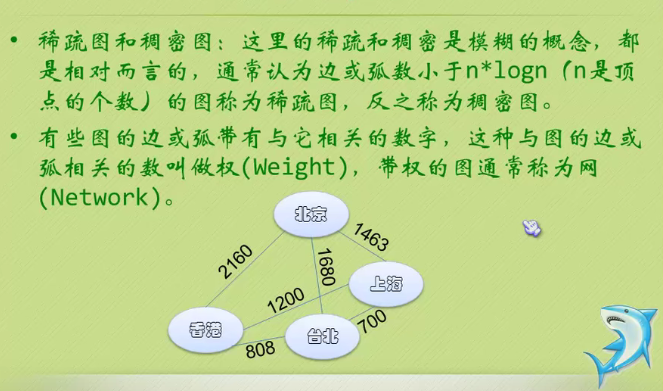
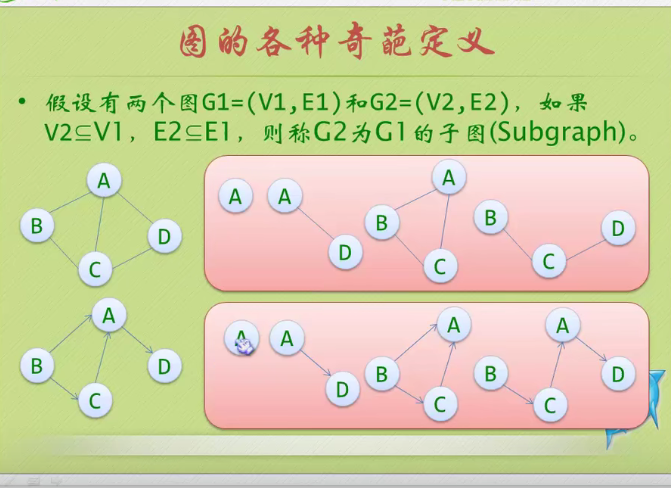
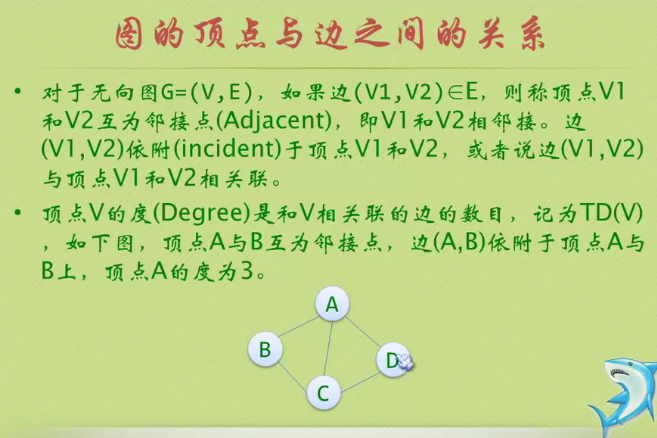
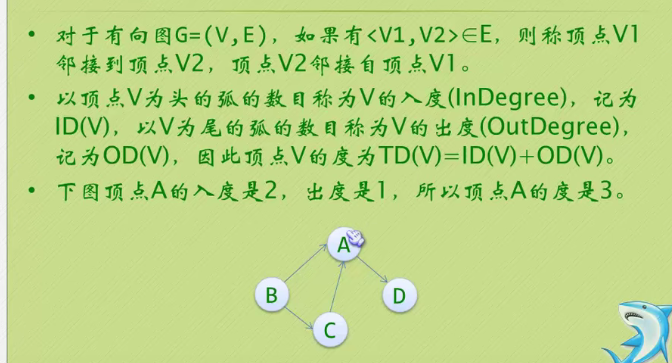
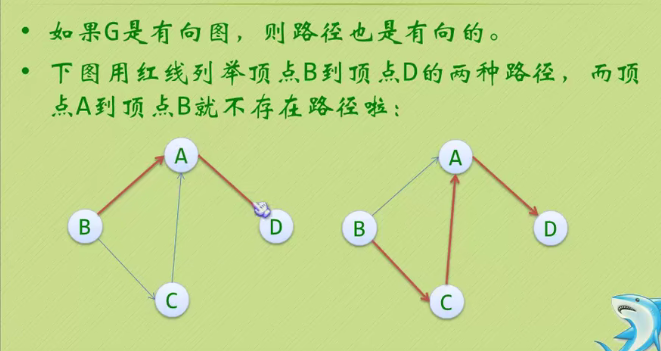
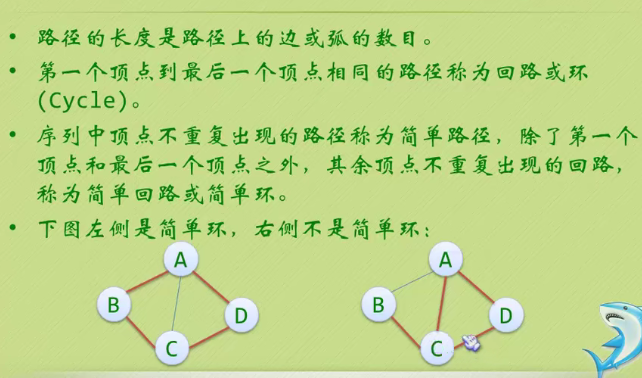
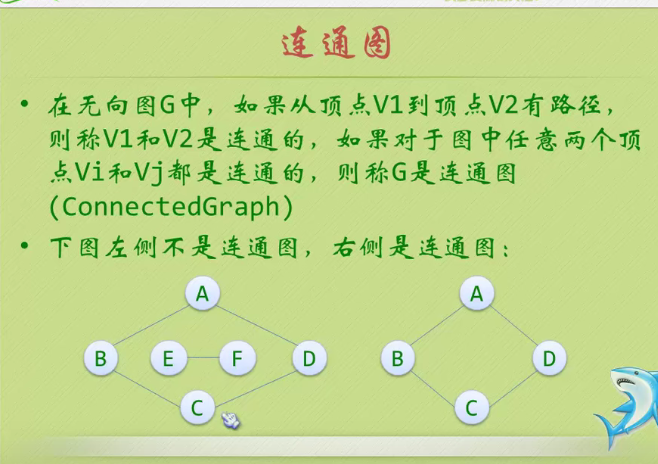
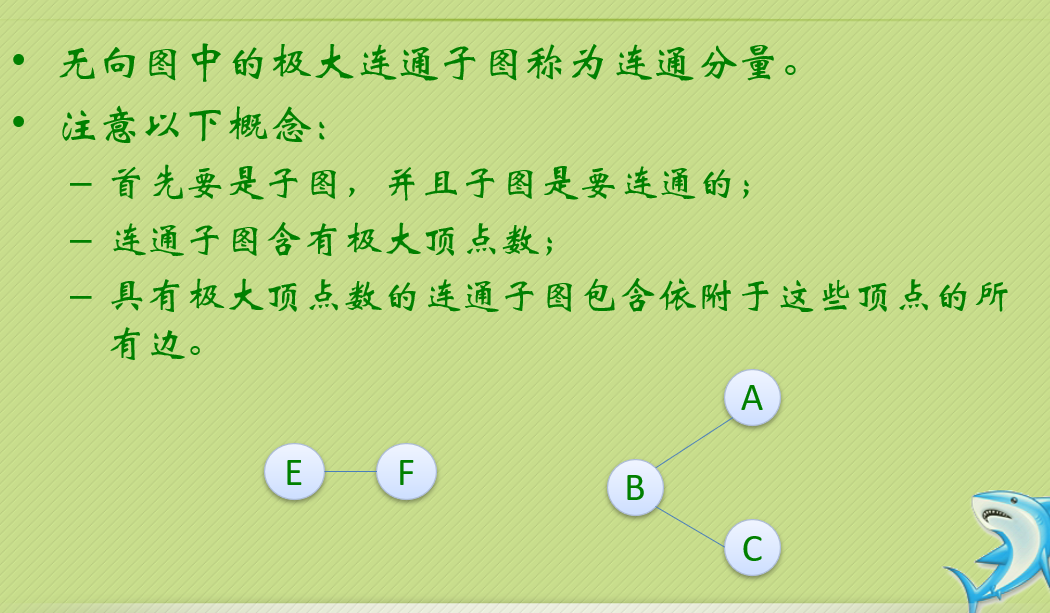
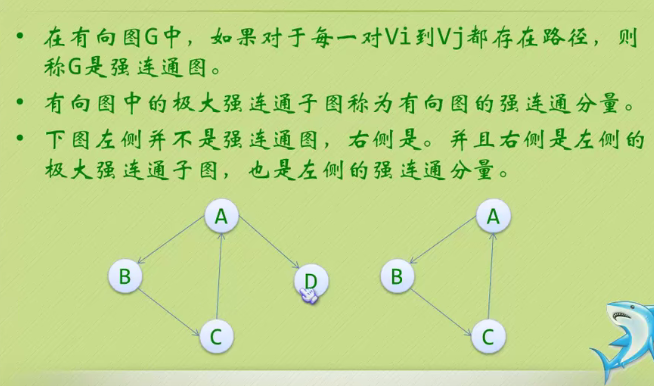
A digraph adds the word "strong"
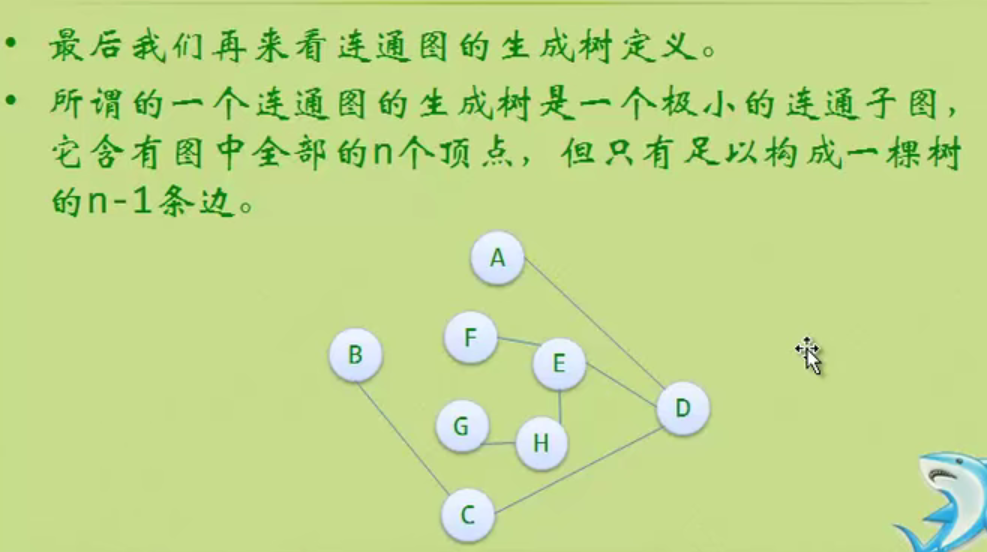
Adding two edges is not a spanning tree
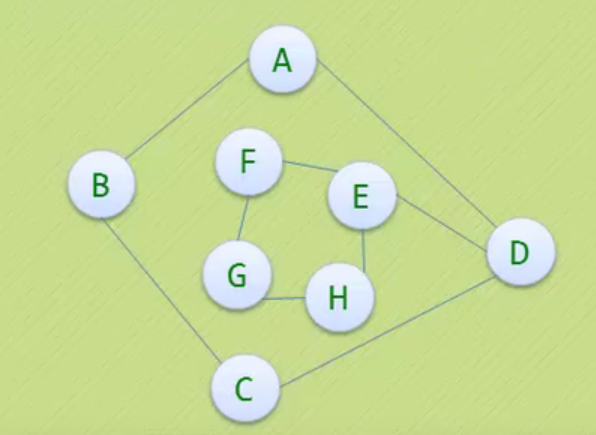
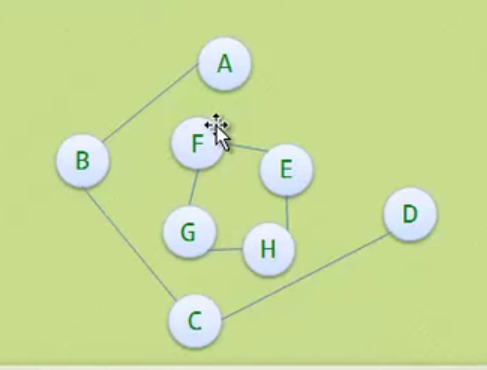
This is not a spanning tree either, because it is two subgraphs
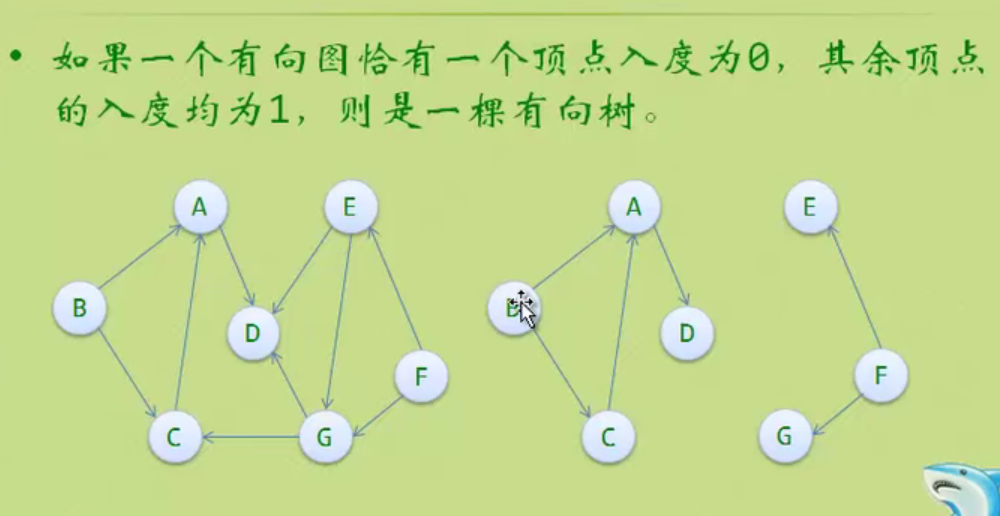
The directed graph on the left becomes the forest on the right. The forest on the right is composed of two directed trees.
Storage structure of graph

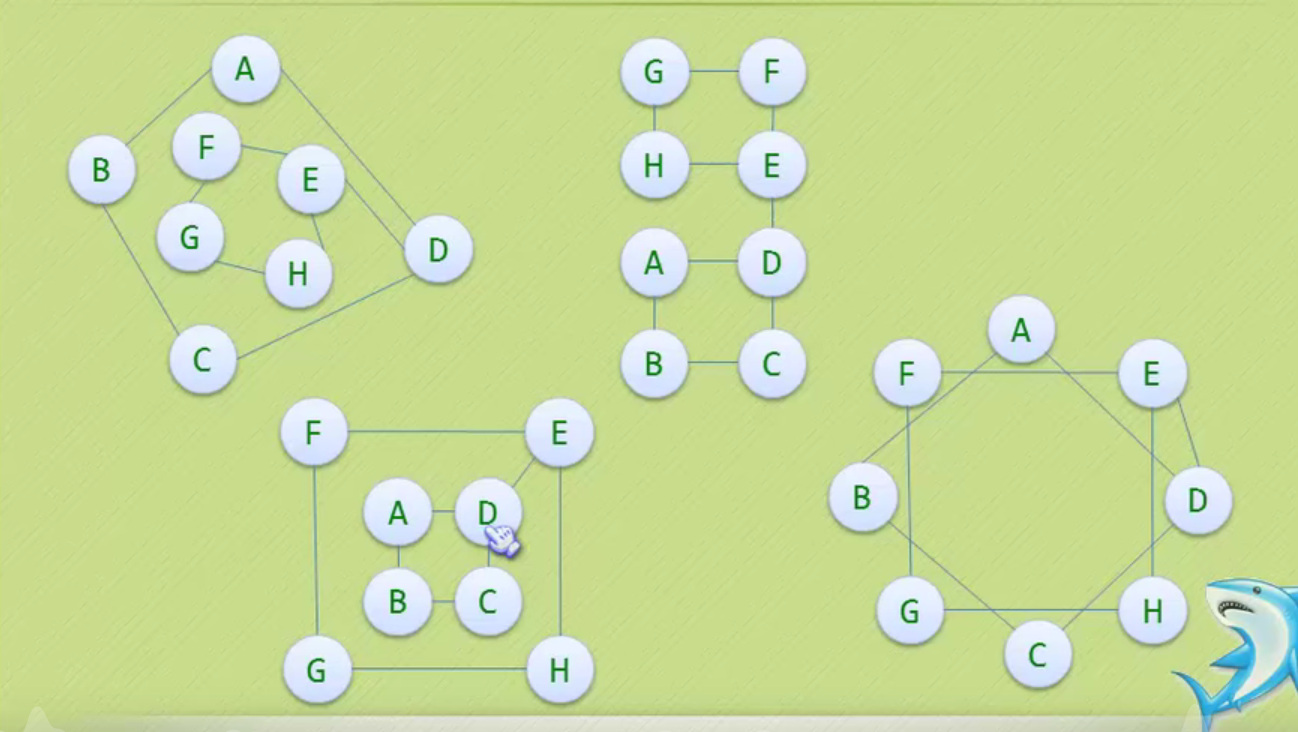
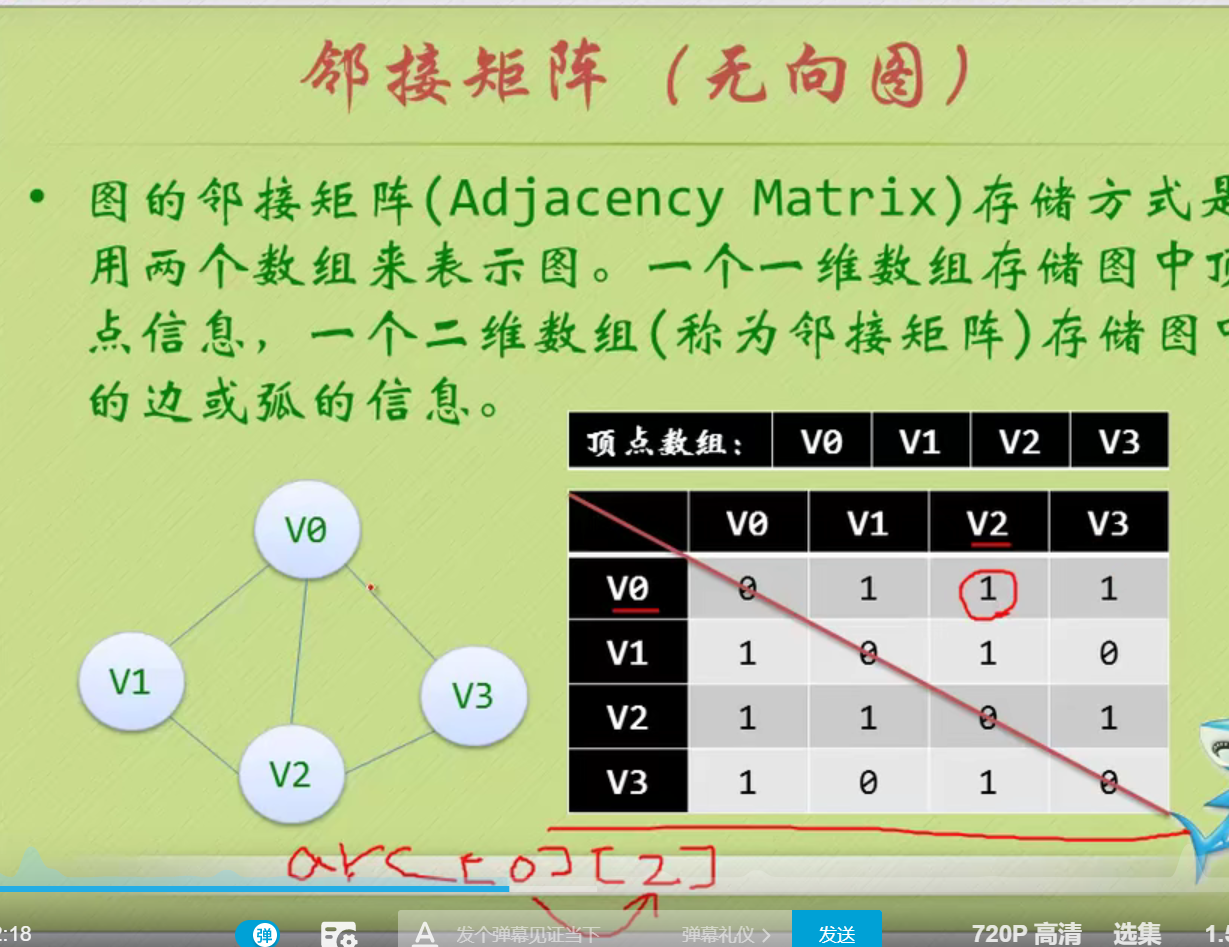
Because it is an undirected graph, the two-dimensional array is symmetrical.
adjacency matrix


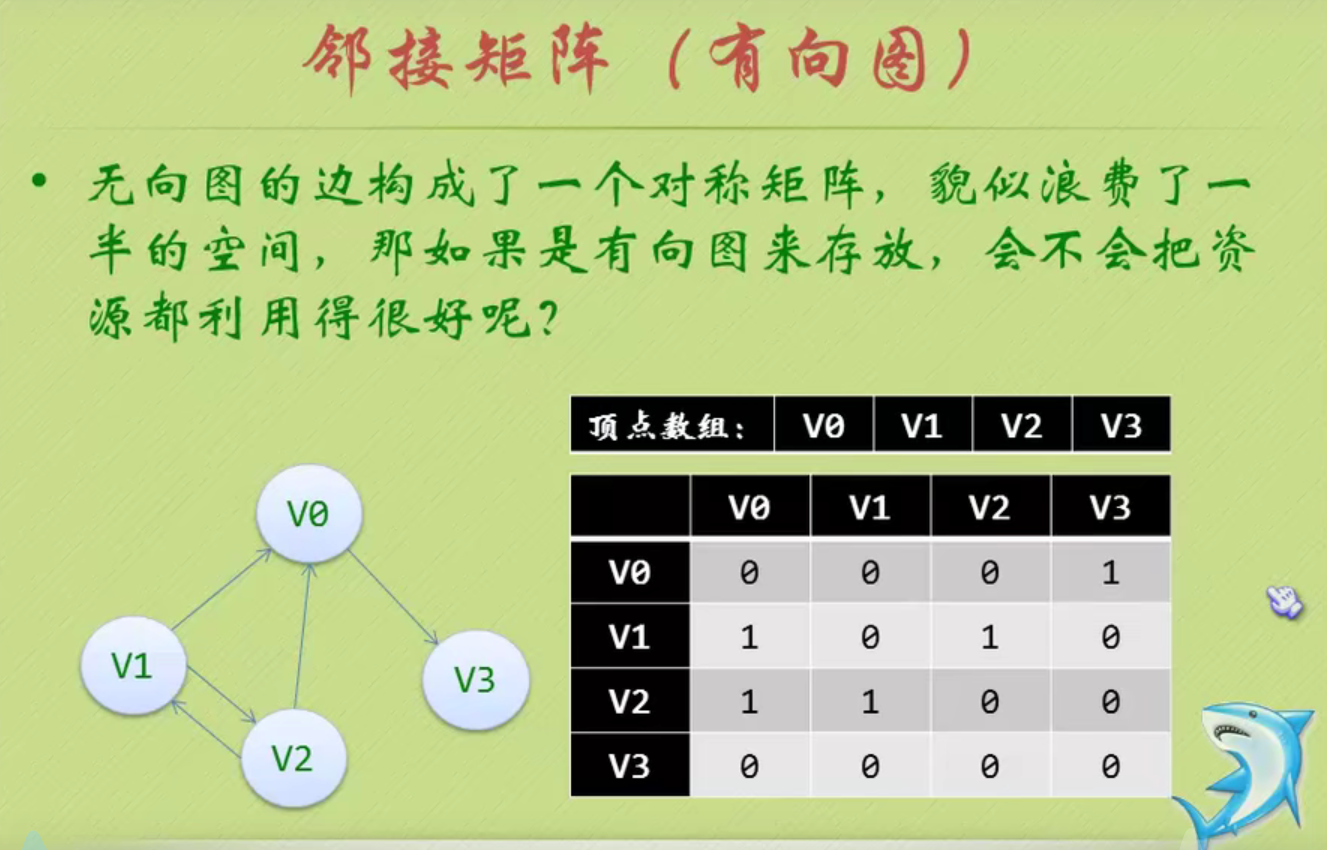

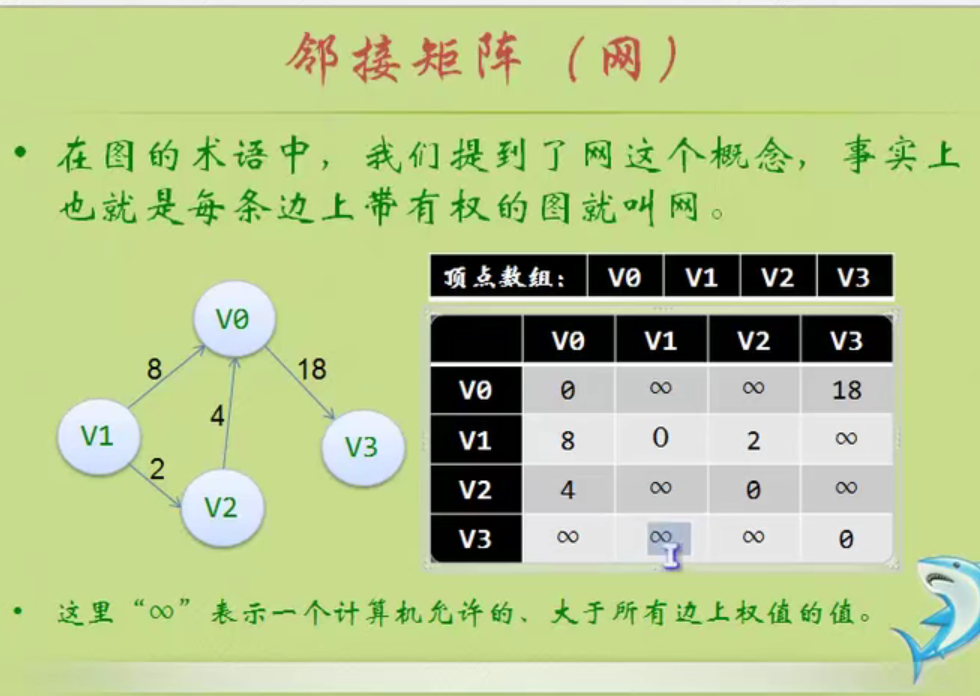

Adjacency matrix code definition of undirected graph and directed graph
// The time complexity is O(n+n^2+e)
#define MAXVEX 100 // max vertex
#define INFINITY 65535 // 65535 is used to represent infinity
typedef struct
{
char vexs[MAXVEX]; // Vertex table
int arc[MAXVEX][MAXVEX]; // adjacency matrix
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} MGraph;
char flag;
// The adjacency matrix of undirected network graph is established
void CreateMGraph(MGraph *G)
{
int i, j, k, w;
int flag;
printf("Please enter whether to generate undirected or directed, undirected input 0, directed input 1:\n");
cin>>flag;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
for( i=0; i < G->numVertexes; i++ )
{
scanf("%c", &G->vexs[i]);
}
for( i=0; i < G->numVertexes; i++ )
{
for( j=0; j < G->numVertexes; j++ )
{
G->arc[i][j] = INFINITY; // Adjacency matrix initialization
}
}
if(flag==0)
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j]; // Is an undirected net graph, symmetric matrix
}
}
else
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
}
}
}
Adjacency table
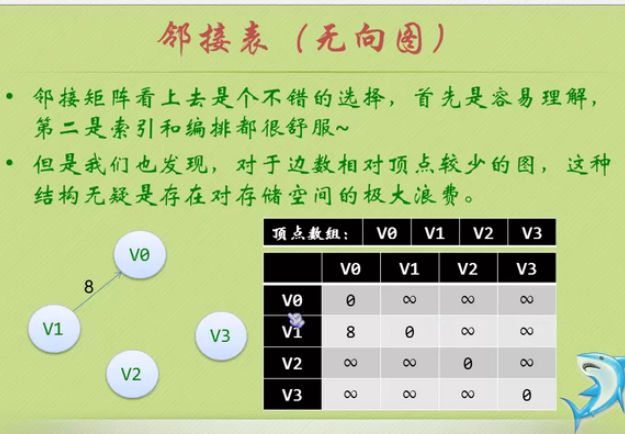

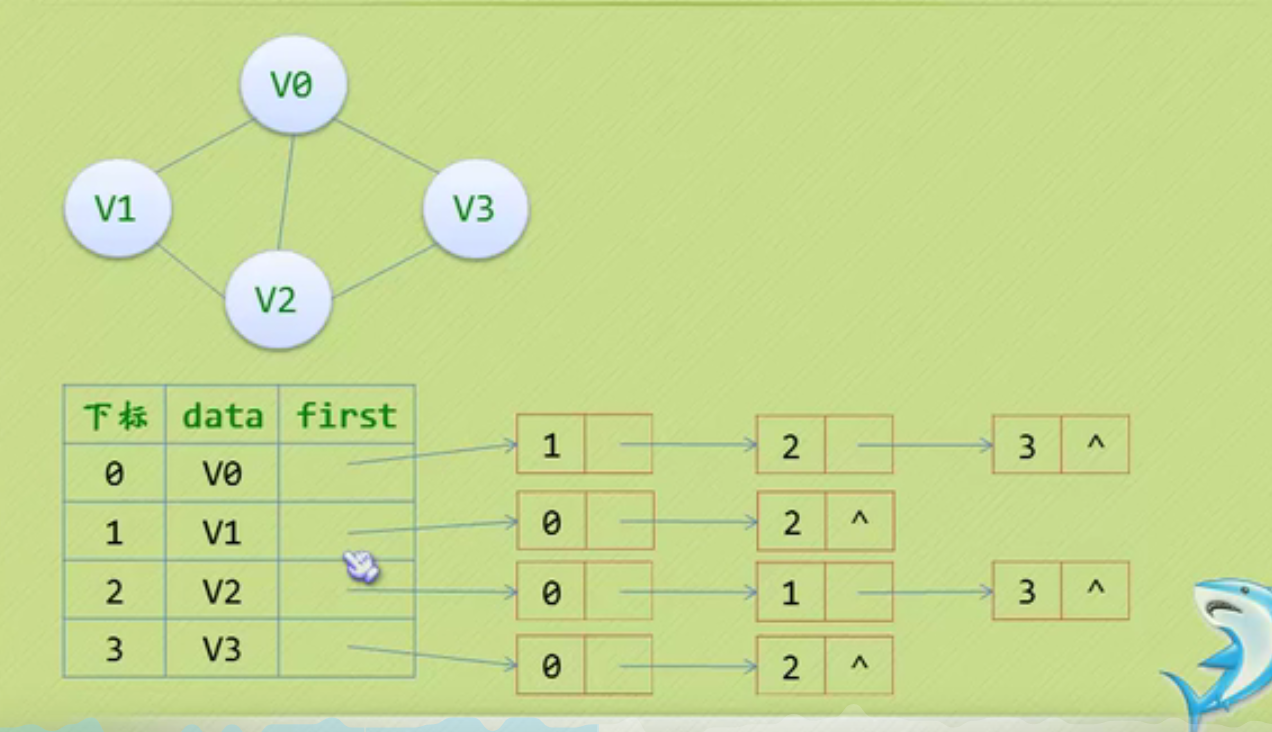
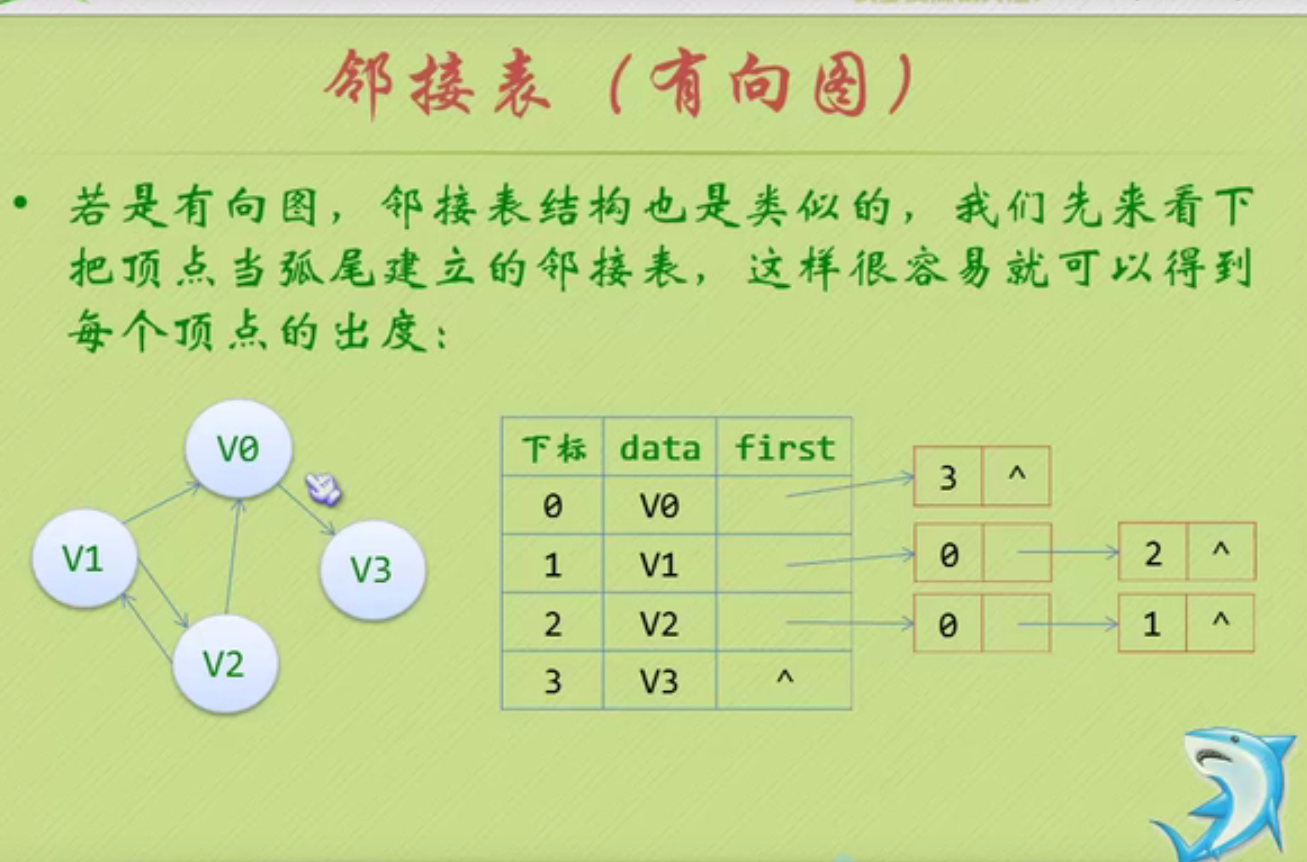
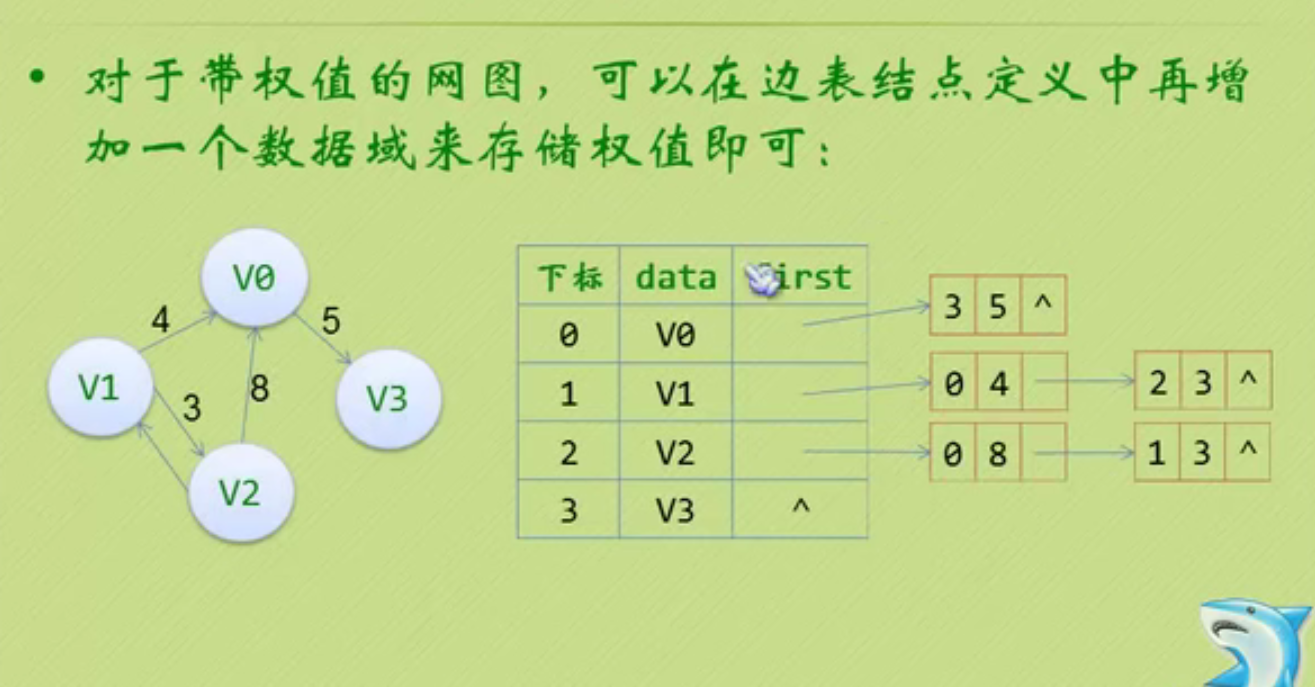
#define MAXVEX 100
//Edge table node
typedef struct EdgeTNode
{
int vertx;//adjacent vertex
int weight;//weight
EdgeTNode *next;//
}EdgeTNode;
//Vertex table node
typedef struct VertxTNode
{
char data; //Vertex domain vertex information
EdgeTNode *firstedge; // Point to the first adjacent node
}VertxTNode ,Vertx[MAXVEX];
//Overall diagram
typedef struct
{
Vertx vertx_;
int numVertexes, numEdges; // The current number of vertices and edges in the graph
}Graph_LinJieT;
//establish
void CreatLinJie(Graph_LinJieT *G)
{
int i,j ,k;
EdgeTNode *e;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
for( i=0;i<G->numVertexes;i++)
{
G->vertx_[i].firstedge=NULL;//initialization
}
for(k=0;k<G->numEdges;k++)
{
//The header insertion used here is the opposite of the adjacency table in the figure, but it also achieves the goal in the end
printf("Please enter an edge(Vi,Vj)Vertex sequence number on:\n");
scanf("%d %d", &i, &j);
//i is adjacent to j on the left
e = (EdgeTNode *)malloc(sizeof(EdgeTNode));
e->vertx=j;
e->next=G->vertx_[i].firstedge;//For example, input (0, 1) 1 will point to NULL
G->vertx_[i].firstedge=e;
//If it is an undirected graph, you have to execute the following statement
//j is adjacent on the left, and the serial number is i
e = (EdgeTNode *)malloc(sizeof(EdgeTNode));
e->vertx=i;
e->next=G->vertx_[j].firstedge;//For example, input (0, 1) 1 will point to NULL
G->vertx_[j].firstedge=e;
}
}
//Textbook answer:
#define MAXVEX 100
typedef struct EdgeNode // Edge table node
{
int adjvex; // The adjacent point field stores the subscript corresponding to the vertex
int weight; // It is used to store weights. It is not required for non network graphs
struct EdgeNode *next; // Chain domain, pointing to the next adjacent node
} EdgeNode;
typedef struct VertexNode // Vertex table node
{
char data; // Vertex domain, storing vertex information
EdgeNode *firstEdge; // Edge header pointer
} VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} GraphAdjList;
// Establish the adjacency table structure of graph
void CreateALGraph(GraphAdjList *G)
{
int i, j, k;
EdgeNode *e;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
// Read vertex information and establish vertex table
for( i=0; i < G->numVertexes; i++ )
{
scanf("%c", &G->adjList[i].data);
G->adjList[i].firstEdge = NULL; // Initialization set to empty table
}
//This is an undirected graph
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Vertex sequence number on:\n");
scanf("%d %d", &i, &j);
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = j; // Adjacency serial number is j
e->next = G->adjList[i].firstEdge;
G->adjList[i].firstEdge = e;
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = i; // Adjacency serial number is i
e->next = G->adjList[j].firstEdge;
G->adjList[j].firstEdge = e;
}
}
Orthogonal list
First, the adjacency table has out degree and the inverse adjacency table has in degree. The two add up to a cross linked list

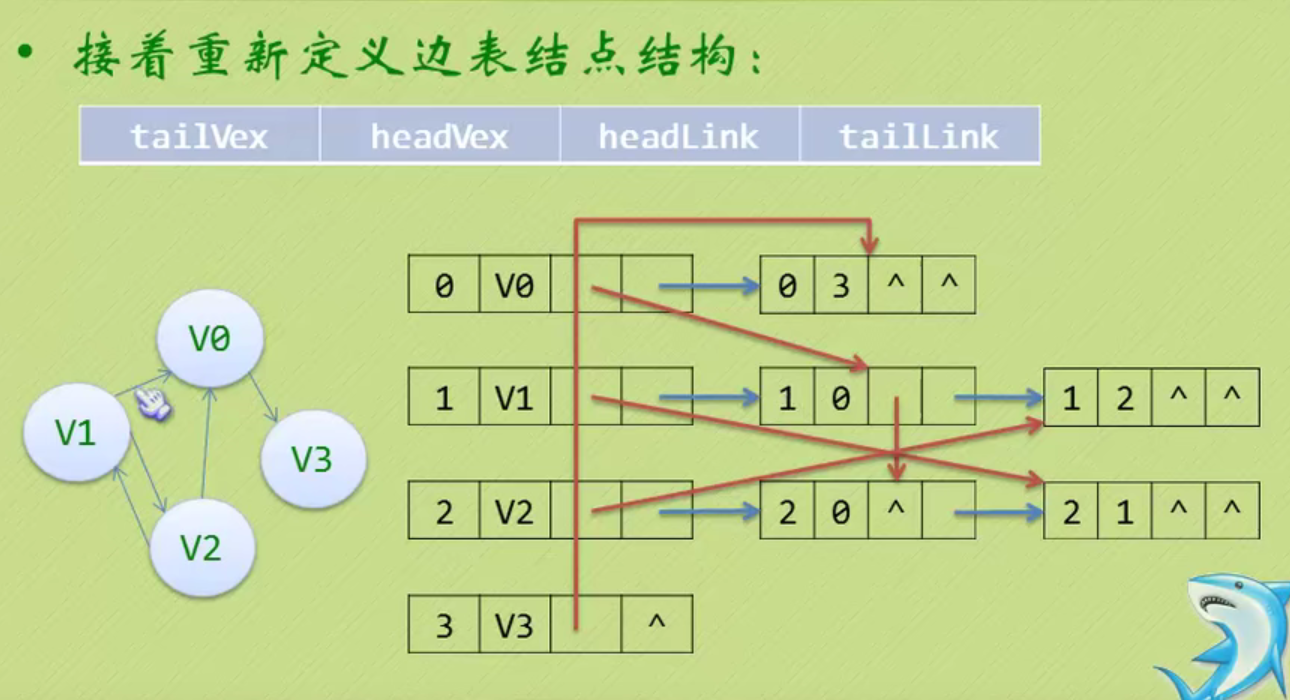
Blue stands for out adjacency table
Red stands for read in - inverse adjacency table


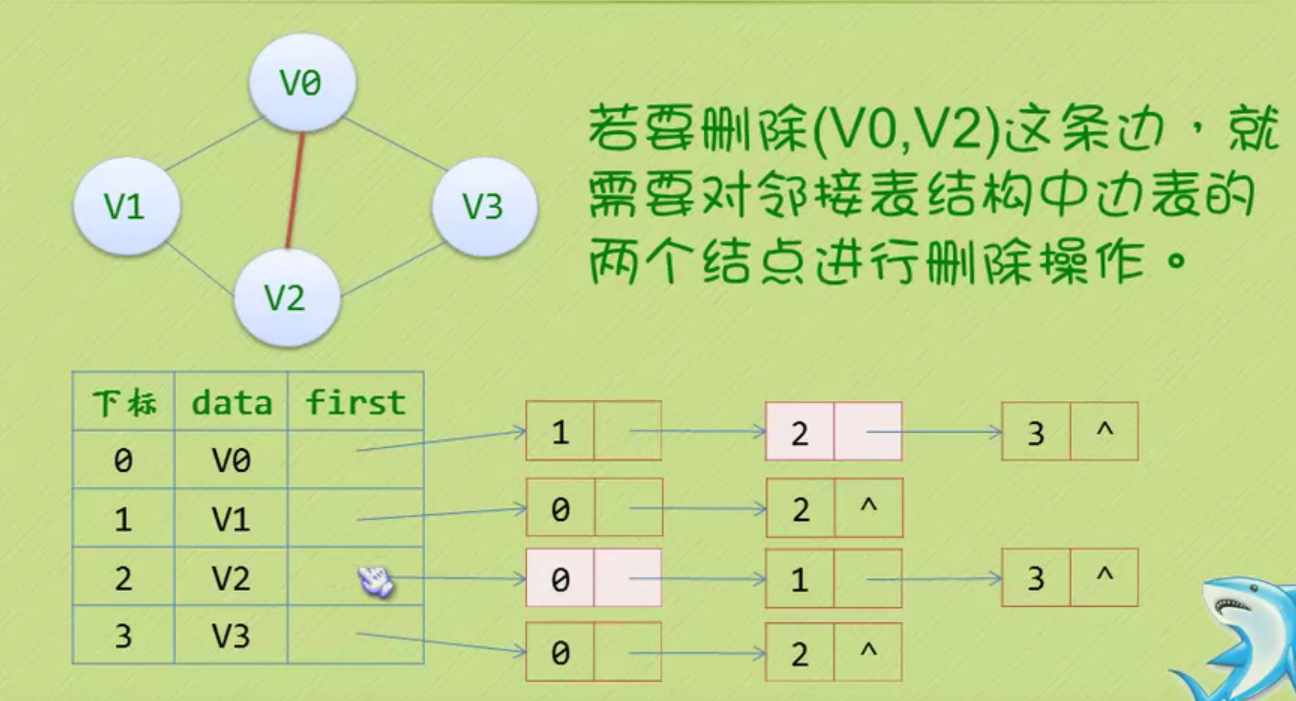
Adjacency multiple table

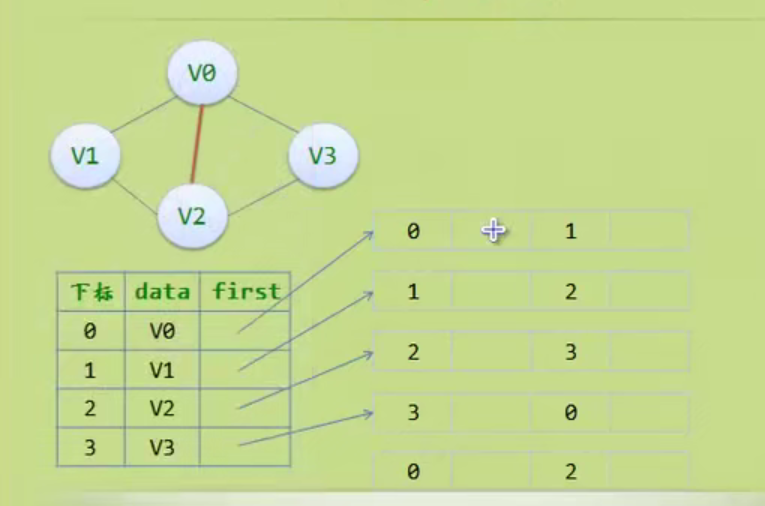
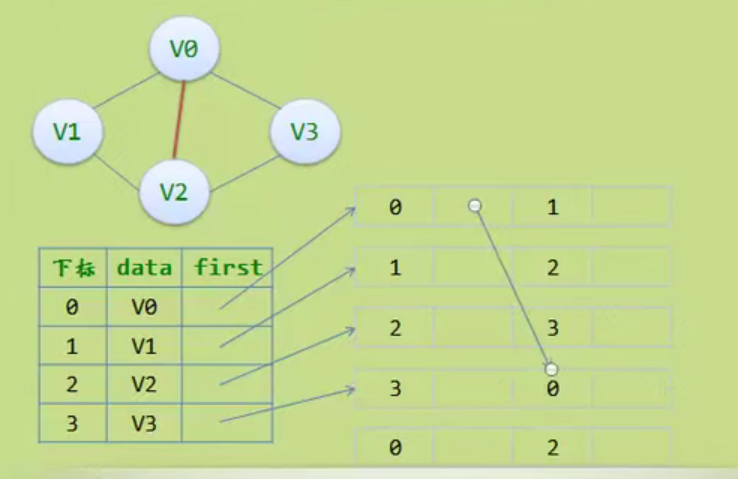
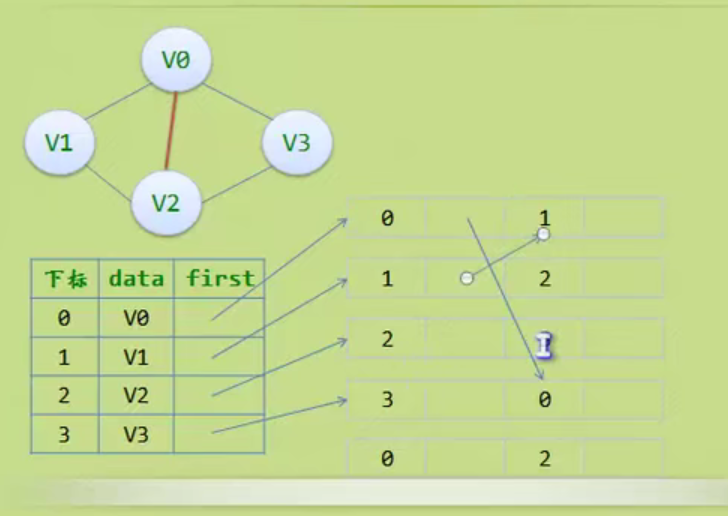
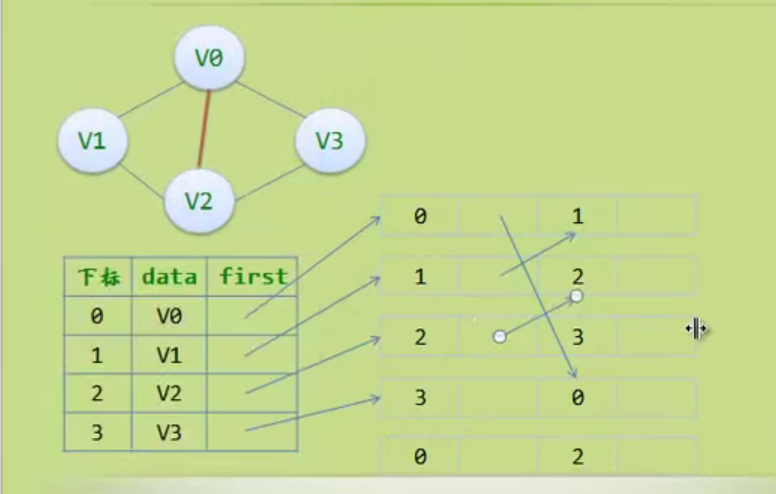
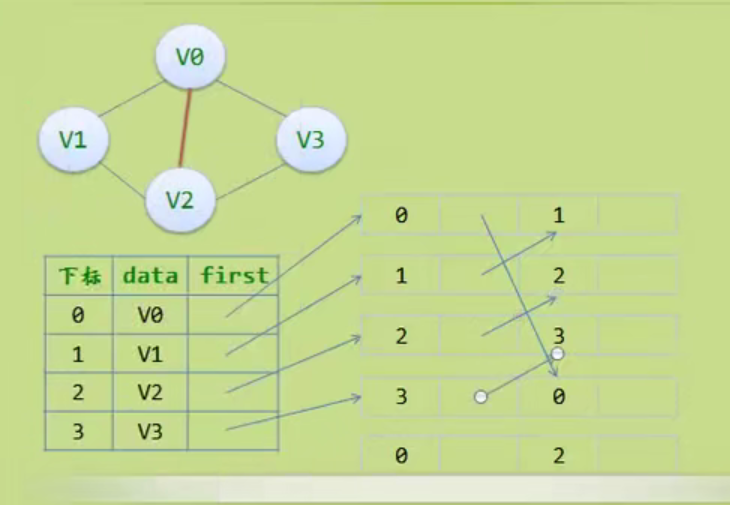
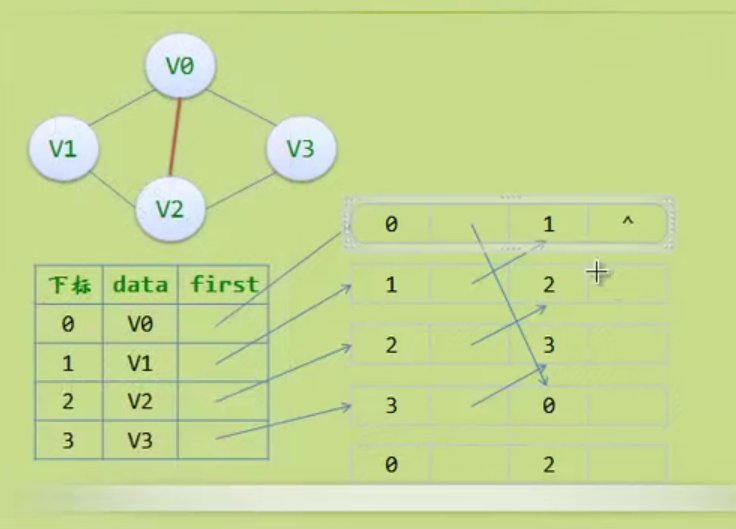
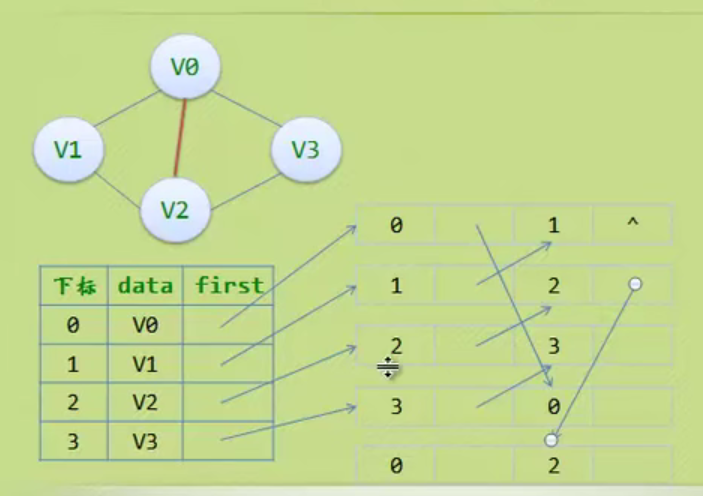
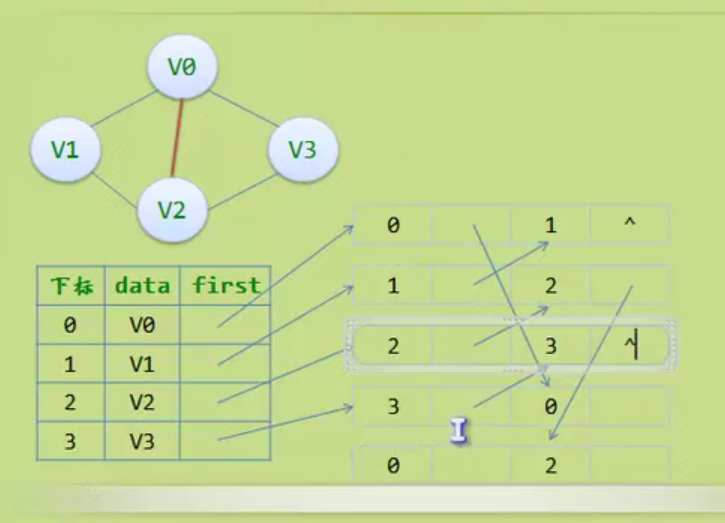
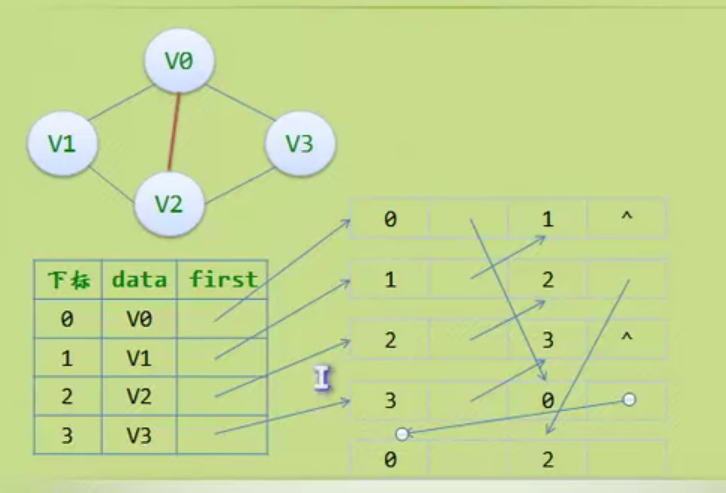
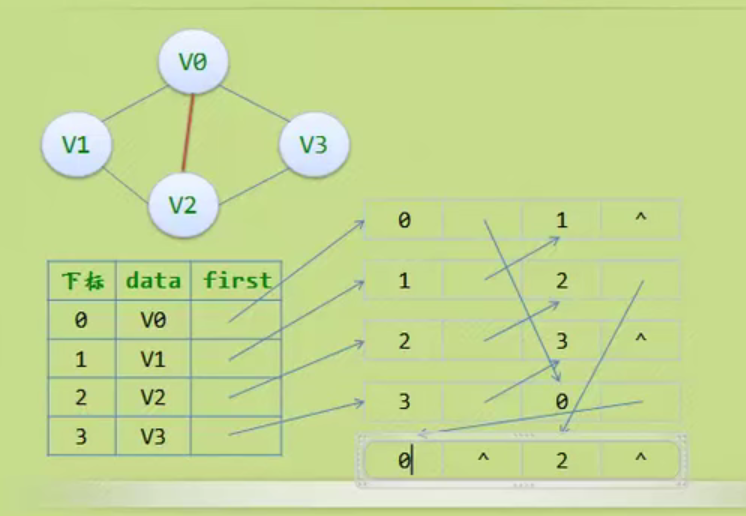
Edge set array
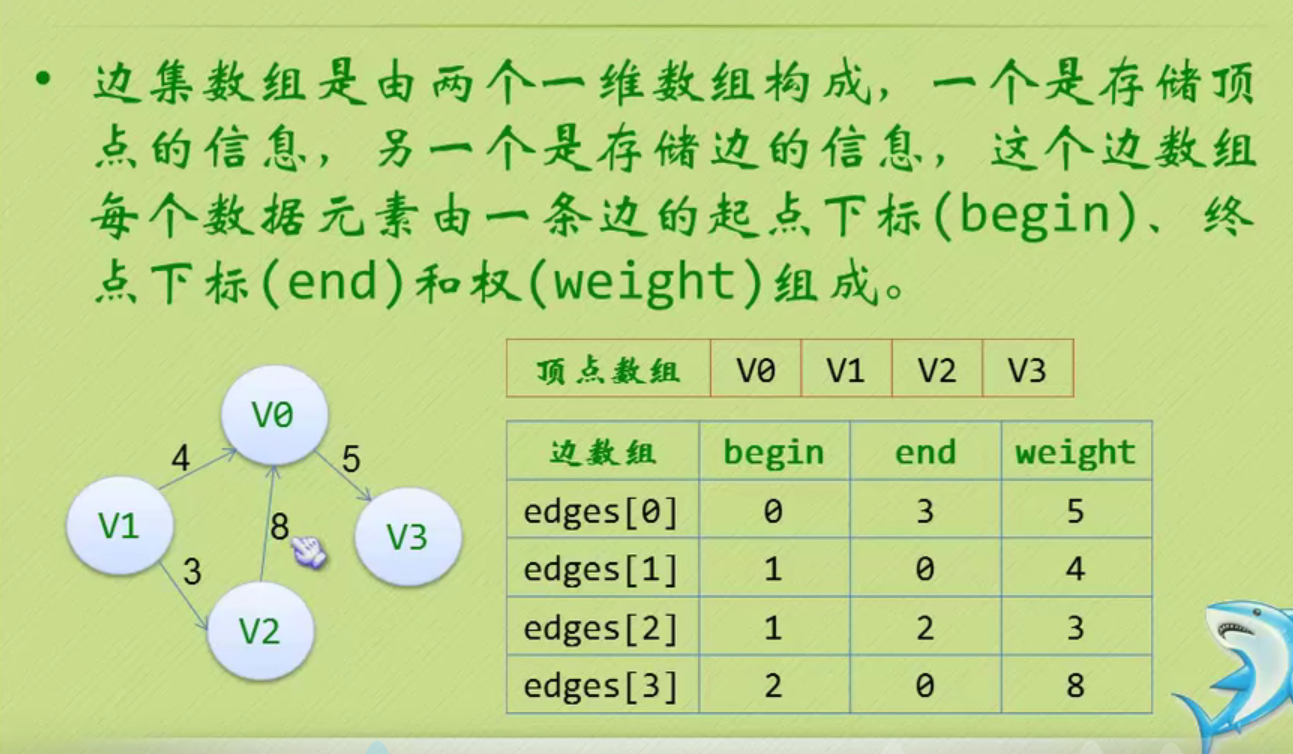
Freud's Iceberg Theory
Graph traversal - depth first traversal DFS


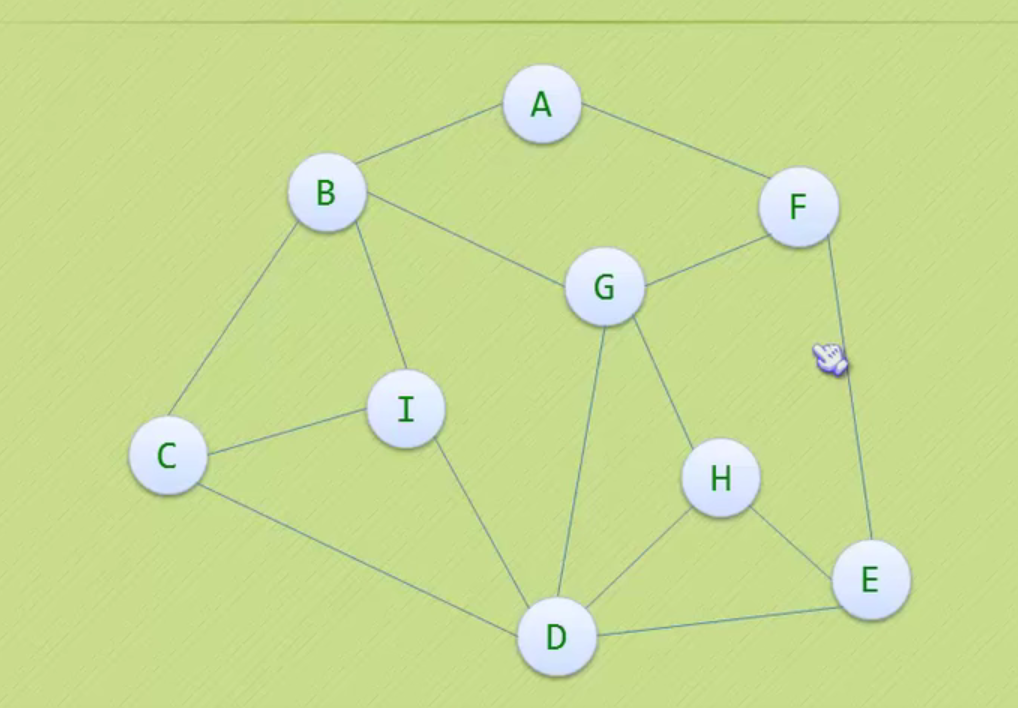

If the point to the right of a point has passed, retreat to the previous point

The walking route is shown in the following figure:
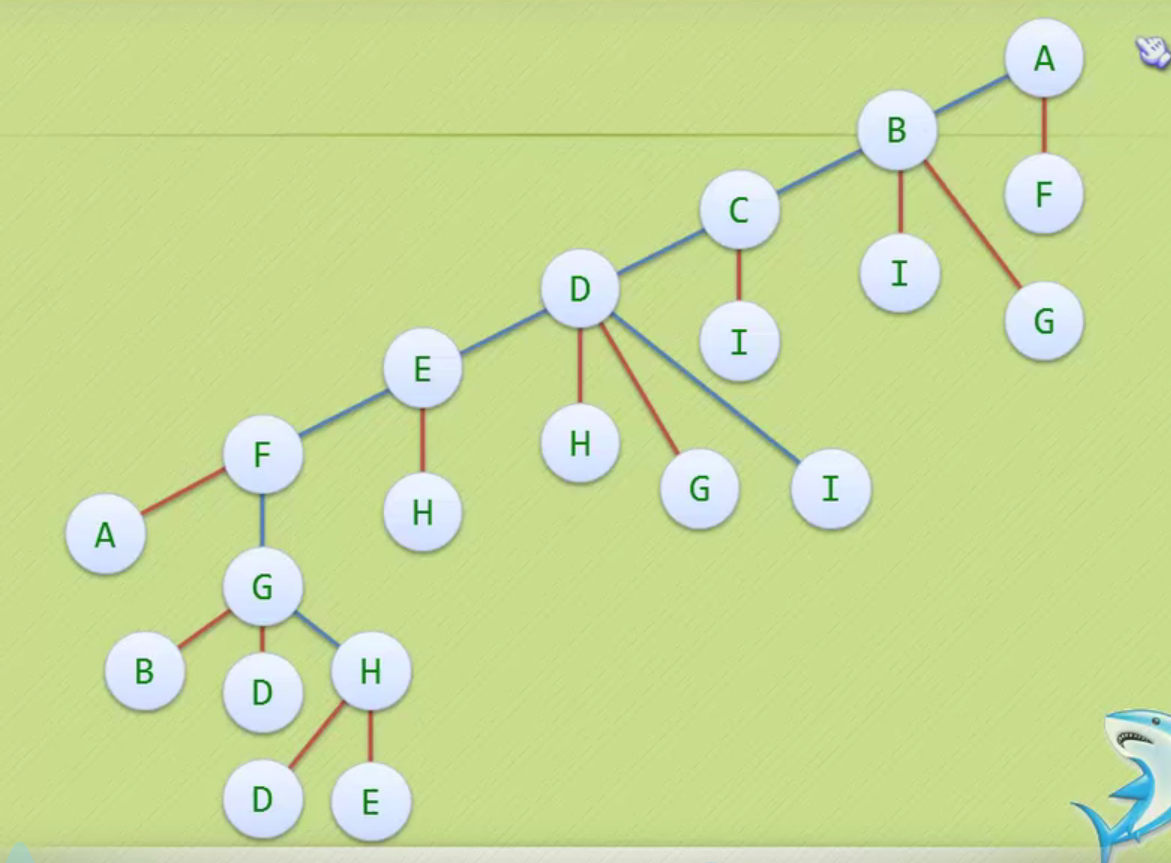
The blue one is accessible, the red one is visited, and can't go.
Depth traversal of adjacency matrix
The following code is based on the structure of adjacency matrix for depth traversal
#include <iostream>
using namespace std;
#define MAXVEX 100 // max vertex
#define INFINITY 65535 // 65535 is used to represent infinity
typedef struct
{
char vexs[MAXVEX]; // Vertex table
int arc[MAXVEX][MAXVEX]; // adjacency matrix
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} MGraph;
// The adjacency matrix of undirected network graph is established
void CreateMGraph(MGraph *G)
{
int i, j, k, w;
int flag;
printf("Please enter whether to generate undirected or directed, undirected input 0, directed input 1:\n");
cin>>flag;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
for( i=0; i < G->numVertexes; i++ )
{
scanf("%c", &G->vexs[i]);
}
for( i=0; i < G->numVertexes; i++ )
{
for( j=0; j < G->numVertexes; j++ )
{
G->arc[i][j] = INFINITY; // Adjacency matrix initialization
}
}
if(flag==0)//Undirected
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j]; // Is an undirected net graph, symmetric matrix
}
}
else//Directed
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
}
}
}
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // Here, we define Boolean as boolean type, and its value is TRUE or FALSE
Boolean visited[MAX]; // Array of access flags
void DFS(MGraph G,int i)
{
visited[i]=true;//Vertex i has been accessed
cout<<G.vexs[i]<<endl;//Output visited vertices
for(int j=0;j<G.numVertexes;j++)
{
if(G.arc[i][j]==1 && !visited[j])//Vertex i forms an edge with vertex j, and vertex j has not been accessed
{
DFS(G,j);//recursion
}
}
}
Adjacency table depth traversal
The following code performs depth traversal in the structure of adjacency table
#include <iostream>
using namespace std;
#define MAXVEX 100
typedef struct EdgeNode // Edge table node
{
int adjvex; // The adjacent point field stores the subscript corresponding to the vertex
int weight; // It is used to store weights. It is not required for non network graphs
struct EdgeNode *next; // Chain domain, pointing to the next adjacent node
} EdgeNode;
typedef struct VertexNode // Vertex table node
{
char data; // Vertex domain, storing vertex information
EdgeNode *firstEdge; // Edge header pointer
} VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} GraphAdjList;
// Establish the adjacency table structure of graph
void CreateALGraph(GraphAdjList *G)
{
int i, j, k;
EdgeNode *e;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
// Read vertex information and establish vertex table
for( i=0; i < G->numVertexes; i++ )
{
scanf("%c", &G->adjList[i].data);
G->adjList[i].firstEdge = NULL; // Initialization set to empty table
}
//This is an undirected graph
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Vertex sequence number on:\n");
scanf("%d %d", &i, &j);
//Head insertion
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = j; // Adjacency serial number is j
e->next = G->adjList[i].firstEdge;
G->adjList[i].firstEdge = e;
e = (EdgeNode *)malloc(sizeof(EdgeNode));
e->adjvex = i; // Adjacency serial number is i
e->next = G->adjList[j].firstEdge;
G->adjList[j].firstEdge = e;
}
}
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // Here, we define Boolean as boolean type, and its value is TRUE or FALSE
Boolean visited[MAX]; // Array of access flags
//Depth traversal we traverse with the rules of adjacency table
void DFS(GraphAdjList GL,int i)
{
EdgeNode *e;
visited[i]= true;//Indicates that you have visited
cout<<GL.adjList[i].data<<endl;//Output visited vertices
//This loop traverses the edges adjacent to vertex i
while(e)
{
if(!visited[e->adjvex]);
{
DFS(GL,e->adjvex);
}
e=e->next;//e points to the next vertex adjacent to i
}
}
void DFSTraverse(GraphAdjList GL)
{
for(int i=0;i<GL.numVertexes;i++)
{
visited[i]=FALSE;//All default to 0
}
//Traverse all vertices
for(int i=0;i<GL.numVertexes;i++)
{
if(!visited[i])// Initializing all vertex States is an unreachable state. You can proceed only if you have not accessed them
{
DFS(GL,i); If it is a connected graph, it will be executed only once, and this point has not been accessed
}
}
}
knight's tour


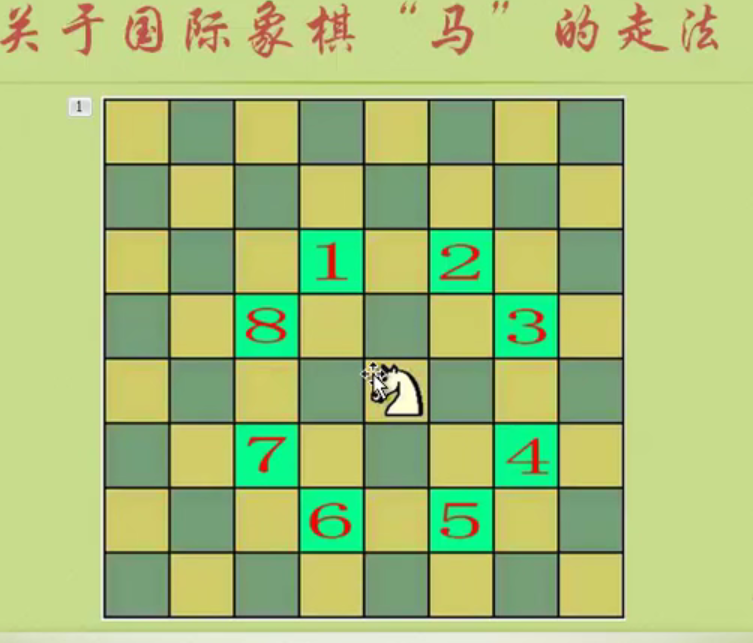
#include <iostream>
#include <ctime>
#include "stdio.h"
using namespace std;
//Chessboard 8 x 8
#define X 8
#define Y 8
//checkerboard
int chess[X][Y];
/**
* The next walkable case based on finding the (x,y) position
* @param x
* @param y
* @param count
* @return
*/
int nextxy(int *x,int *y,int count)
{
//Eight walking methods
switch (count)
{
case 0:
if(*x+2<=X-1 && *y-1>=0 &&chess[*x+2][*y-1]==0)//Jump to the right. You should judge the position of 3 within the chessboard range, and this position has not been traversed
{
*x = *x + 2;
*y = *y - 1;
return 1;
}
break;
case 1:
if(*x+2<=X-1 && *y+1<=Y-1 &&chess[*x+2][*y+1]==0) //The judgment is 4 this position
{
*x = *x + 2;
*y = *y + 1;
return 1;
}
break;
case 2:
if(*x+1<=X-1 && *y-2>=0 &&chess[*x+1][*y-2]==0) //The judgment is 2 this position
{
*x = *x + 1;
*y = *y - 2;
return 1;
}
break;
case 3:
if(*x+1<=X-1 && *y+2<=Y-1 &&chess[*x+1][*y+2]==0) //The judgment is 5 this position
{
*x = *x + 1;
*y = *y + 2;
return 1;
}
break;
case 4:
if(*x-2>=0 && *y-1>=0 &&chess[*x-2][*y-1]==0) //The judgment is 8 this position
{
*x = *x - 2;
*y = *y - 1;
return 1;
}
break;
case 5:
if(*x-2>=0 && *y+1<=Y-1 && chess[*x-2][*y+1]==0) //The judgment is 7 this position
{
*x = *x - 2;
*y = *y + 1;
return 1;
}
break;
case 6:
if(*x-1>=0 && *y-2>=0 && chess[*x-1][*y-2]==0) //The position of 1 is judged
{
*x = *x - 1;
*y = *y - 2;
return 1;
}
break;
case 7:
if(*x-1>=0 && *y+2<=Y-1 &&chess[*x-1][*y+2]==0) //The judgment is 6 this position
{
*x = *x - 1;
*y = *y + 2;
return 1;
}
break;
default:
break;
}
return 0;
}
/**
* Print chessboard
*/
void print()
{
int i,j;
for(i=0;i<X;i++)
{
for(j=0;j<Y;j++)
{
printf("%2d\t", chess[i][j]);
}
cout<<endl;
}
cout<< endl;
}
/**
* Depth first traversal chessboard
* (x,y)Is the starting position
* @param x
* @param y
* @param tag Tag variable tag+1 every step
* @return
*/
int TravelChessBoard(int x,int y,int tag)
{
int x1=x,y1=y,flag=0,count=0;
chess[x][y]=tag;
if(tag == X*Y)
{
//Print chessboard
print();
return 1;
}
//Find the next walking coordinate (x1,y1) of the horse. If flag=1 is found, otherwise it is 0
flag= nextxy(&x1,&y1,count);//Find the next feasible location
//The while here is to ensure that you can go to the next position for the first time
while(flag==0 && count<7)//In the nextxy() function, when some positions have passed, it will return 0. At this time, let count + + try another available next position
{
count++;
flag= nextxy(&x1,&y1,count);
}
while(flag)//Indicates that the next walkable position of the current position has been found
{
if(TravelChessBoard(x1,y1,tag+1))
{
return 1;
}
//If you follow the first x1 y1 step until there is repetition, then go back to the beginning and find the next step of the horse again
//Find the next walking coordinate (x1,y1) of the horse. If flag=1 is found, otherwise it is 0
x1=x;
y1=y;
count++;
//This is the next step up and down
flag= nextxy(&x1,&y1,count);
while(flag==0 && count<7)
{
count++;
flag= nextxy(&x1,&y1,count);
}
}
if(0==flag)
{
chess[x][y]=0;//Look again
}
return 0;
}
void test_KinghtTraverse()
{
int i,j;
clock_t start, finish;
start =clock();
for(i=0;i<X;i++)
{
for(j=0;j<Y;j++)
{
chess[i][j]=0;
}
}
if(!TravelChessBoard(2,0,1))//Starting position: second row, column 0
{
cout<<"Sorry, the horse failed to step on the chessboard!!!"<<endl;
}
finish=clock();
cout<<"Total time for this calculation:"<<(double )(finish-start)/CLOCKS_PER_SEC<<"s"<<endl;//The number of CPU ticks divided by the number of CPU ticks per minute is seconds
}
int main() {
test_KinghtTraverse();
return 0;
}
The starting position of the horse is the second row and column 0
Operation results:
Breadth first traversal BFS

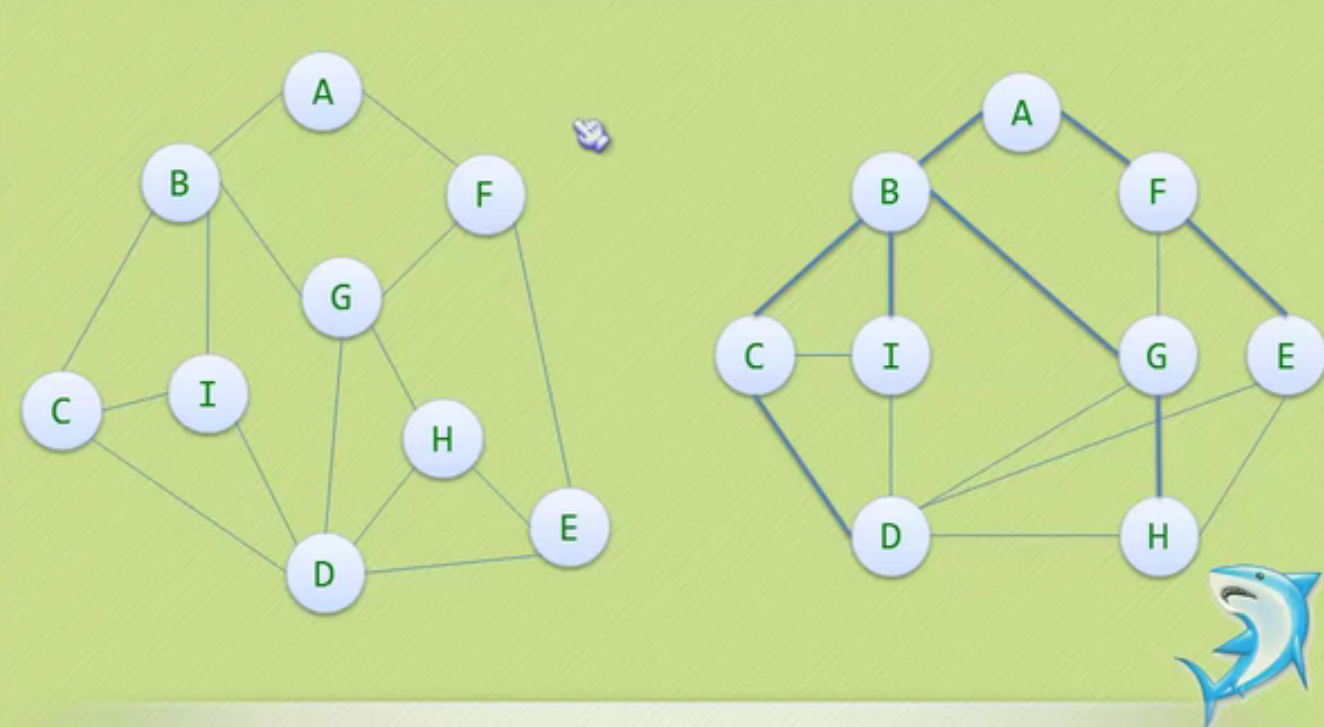
Explain from the figure on the right,
Let's start with A, take the right first principle, go to B first, and then f, because for A, B and F are the closest.
Therefore, the traversal order is ABF CIGE DH
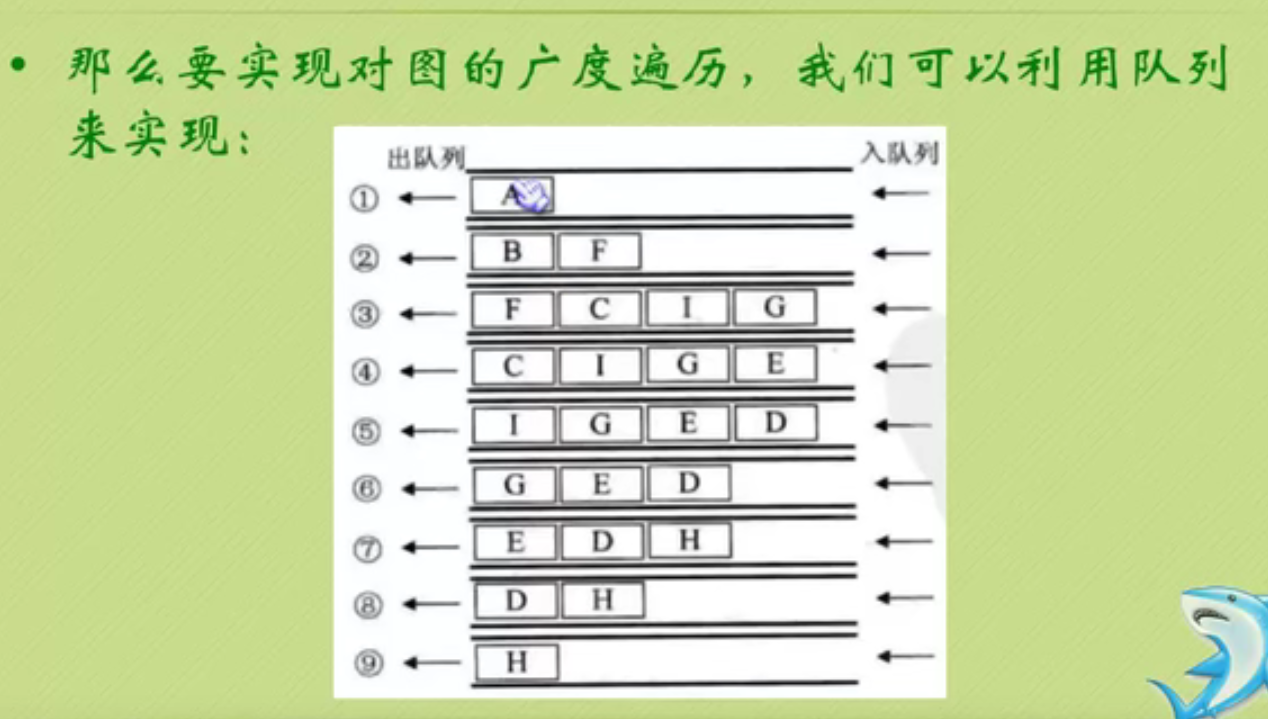
fifo
Adjacency matrix breadth ergodic
//Breadth traversal of adjacency matrix
namespace LinJieMatrix
{
#include <iostream>
using namespace std;
#define MAXVEX 100 // max vertex
#define INFINITY 65535 // 65535 is used to represent infinity
typedef struct
{
char vexs[MAXVEX]; // Vertex table
int arc[MAXVEX][MAXVEX]; // adjacency matrix
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} MGraph;
// The adjacency matrix of undirected network graph is established
void CreateMGraph(MGraph *G)
{
int i, j, k, w;
int flag;
printf("Please enter whether to generate undirected or directed, undirected input 0, directed input 1:\n");
cin>>flag;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
for( i=0; i < G->numVertexes; i++ )
{
scanf("%c", &G->vexs[i]);
}
for( i=0; i < G->numVertexes; i++ )
{
for( j=0; j < G->numVertexes; j++ )
{
G->arc[i][j] = INFINITY; // Adjacency matrix initialization
}
}
if(flag==0)//Undirected
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j]; // Is an undirected net graph, symmetric matrix
}
}
else//Directed
{
for( k=0; k < G->numEdges; k++ )
{
printf("Please enter an edge(Vi,Vj)Subscript on i,subscript j And corresponding rights w:\n"); // This is just an example. Improving the user experience needs to be improved
scanf("%d %d %d", &i, &j, &w);
G->arc[i][j] = w;
}
}
}
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // Here, we define Boolean as boolean type, and its value is TRUE or FALSE
Boolean visited[MAX]; // Array of access flags
// Breadth traversal algorithm of adjacency matrix
void BFSTraverse(MGraph G)
{
int i, j;
Queue Q;
for( i=0; i < G.numVertexes; i++ )
{
visited[i] = FALSE;
}
initQueue( &Q );//Initialize queue
for( i=0; i < G.numVertexes; i++ )
{
if( !visited[i] )
{
printf("%c ", G.vexs[i]);
visited[i] = TRUE;
EnQueue(&Q, i);//Enter queue
while( !QueueEmpty(Q) )
{
DeQueue(&Q, &i);//Out of queue
//Traverse the vertices adjacent to vertex i
for( j=0; j < G.numVertexes; j++ )
{
if( G.arc[i][j]==1 && !visited[j] )//j is the adjacent vertex of i
{
printf("%c ", G.vexs[j]);
visited[j] = TRUE;
EnQueue(&Q, j);//Queue
}
}
}
}
}
}
}
Adjacency table - breadth traversal
//Adjacency table traversal
namespace LinJieTable_BFS {
#include <iostream>
using namespace std;
#define MAXVEX 100
typedef struct EdgeNode // Edge table node
{
int adjvex; // The adjacent point field stores the subscript corresponding to the vertex
int weight; // It is used to store weights. It is not required for non network graphs
struct EdgeNode *next; // Chain domain, pointing to the next adjacent node
} EdgeNode;
typedef struct VertexNode // Vertex table node
{
char data; // Vertex domain, storing vertex information
EdgeNode *firstEdge; // Edge header pointer
} VertexNode, AdjList[MAXVEX];
typedef struct {
AdjList adjList;
int numVertexes, numEdges; // The current number of vertices and edges in the graph
} GraphAdjList;
// Establish the adjacency table structure of graph
void CreateALGraph(GraphAdjList *G) {
int i, j, k;
EdgeNode *e;
printf("Please enter the number of vertices and edges:\n");
scanf("%d %d", &G->numVertexes, &G->numEdges);
// Read vertex information and establish vertex table
for (i = 0; i < G->numVertexes; i++) {
scanf("%c", &G->adjList[i].data);
G->adjList[i].firstEdge = NULL; // Initialization set to empty table
}
//This is an undirected graph
for (k = 0; k < G->numEdges; k++) {
printf("Please enter an edge(Vi,Vj)Vertex sequence number on:\n");
scanf("%d %d", &i, &j);
//Head insertion
e = (EdgeNode *) malloc(sizeof(EdgeNode));
e->adjvex = j; // Adjacency serial number is j
e->next = G->adjList[i].firstEdge;
G->adjList[i].firstEdge = e;
e = (EdgeNode *) malloc(sizeof(EdgeNode));
e->adjvex = i; // Adjacency serial number is i
e->next = G->adjList[j].firstEdge;
G->adjList[j].firstEdge = e;
}
}
#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean; // Here, we define Boolean as boolean type, and its value is TRUE or FALSE
Boolean visited[MAX]; // Array of access flags
//Breadth traversal we traverse by the rules of adjacency table
void BFS(GraphAdjList G) {
int i, j;
Queue Q;//queue
for (i = 0; i < G.numVertexes; i++) {
visited[i] = FALSE;
}
initQueue(&Q);//Initialize queue
for (i = 0; i < G.numVertexes; i++) {
if (!visited[i]) {
printf("%c ", G.adjList[i].data);
visited[i] = TRUE;
EnQueue(&Q, i);//Enter queue
while (!QueueEmpty(Q)) {
DeQueue(&Q, &i);//Out of queue
//Traverse the vertices adjacent to vertex i
for (j = 0; j < G.numVertexes; j++) {
EdgeNode *e;//Adjacent edge node
e = G.adjList[i].firstEdge;//e points to the adjacent edge node of i
if (e && !visited[e->adjvex])//E - > adjvex is the vertex j
{
printf("%c ", e->adjvex);
visited[e->adjvex] = TRUE;
EnQueue(&Q, e->adjvex);//Queue
}
e = e->next;//Point to the next edge node adjacent to i
}
}
}
}
}
}
Weighted minimum spanning tree
Prim algorithm
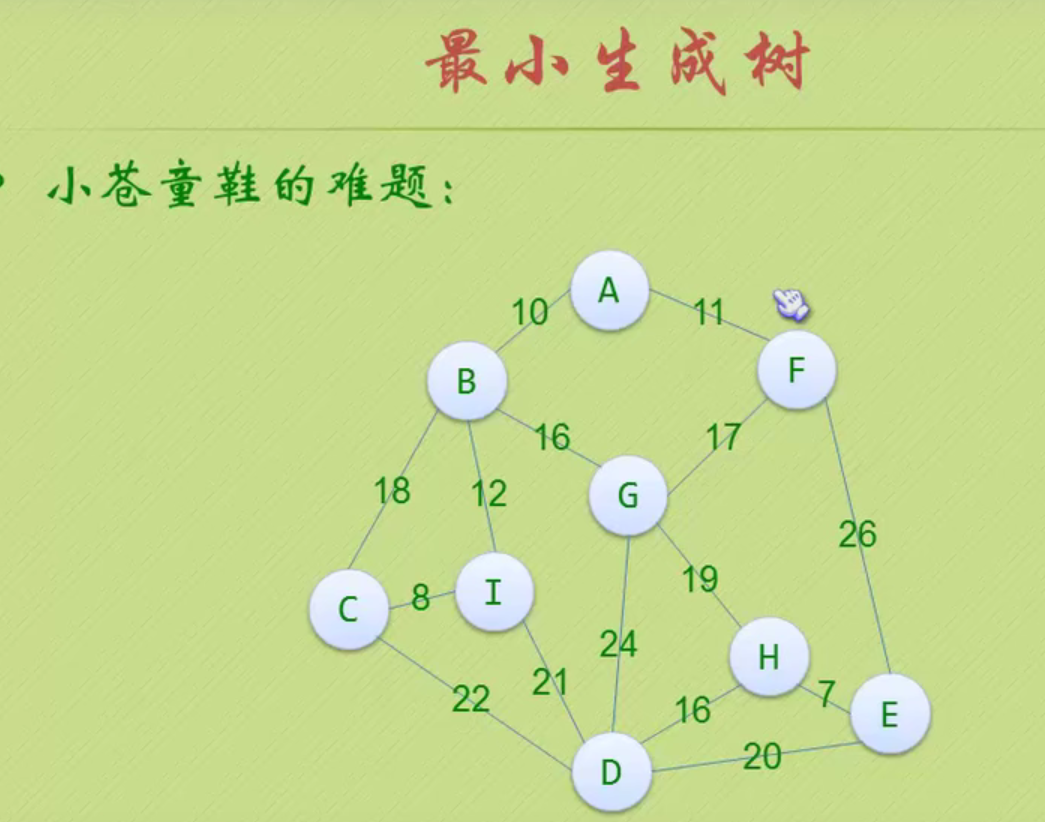
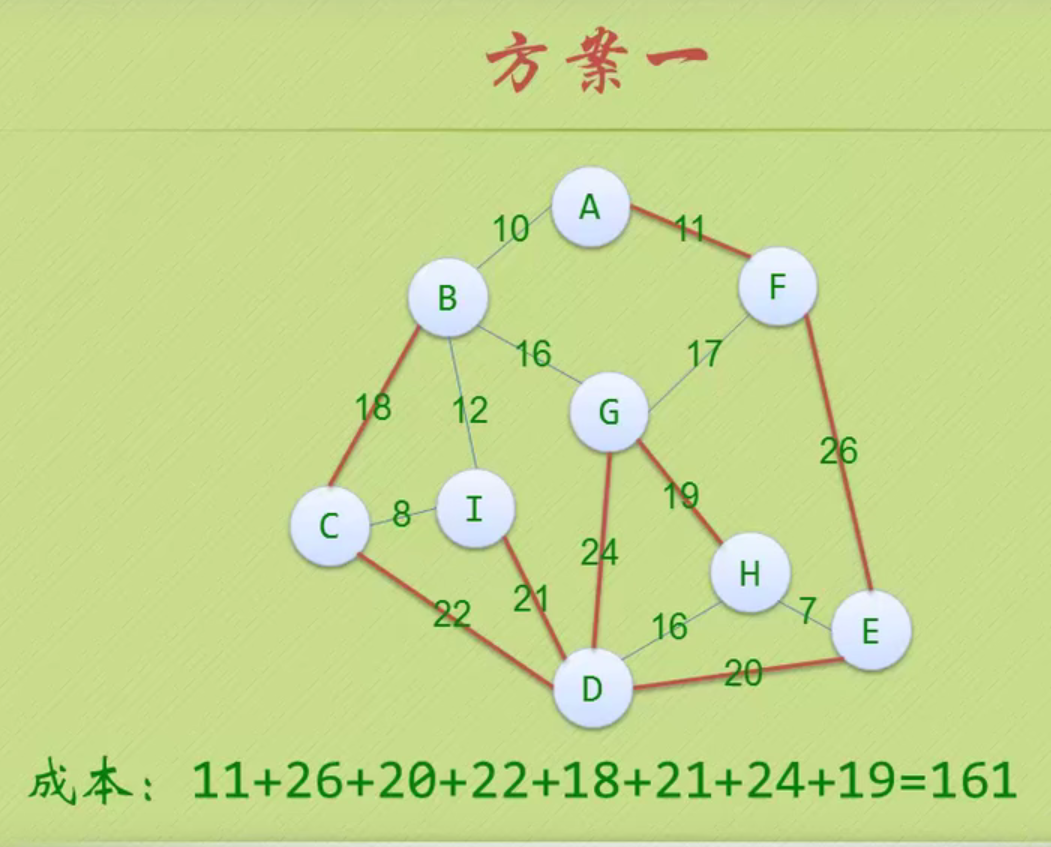
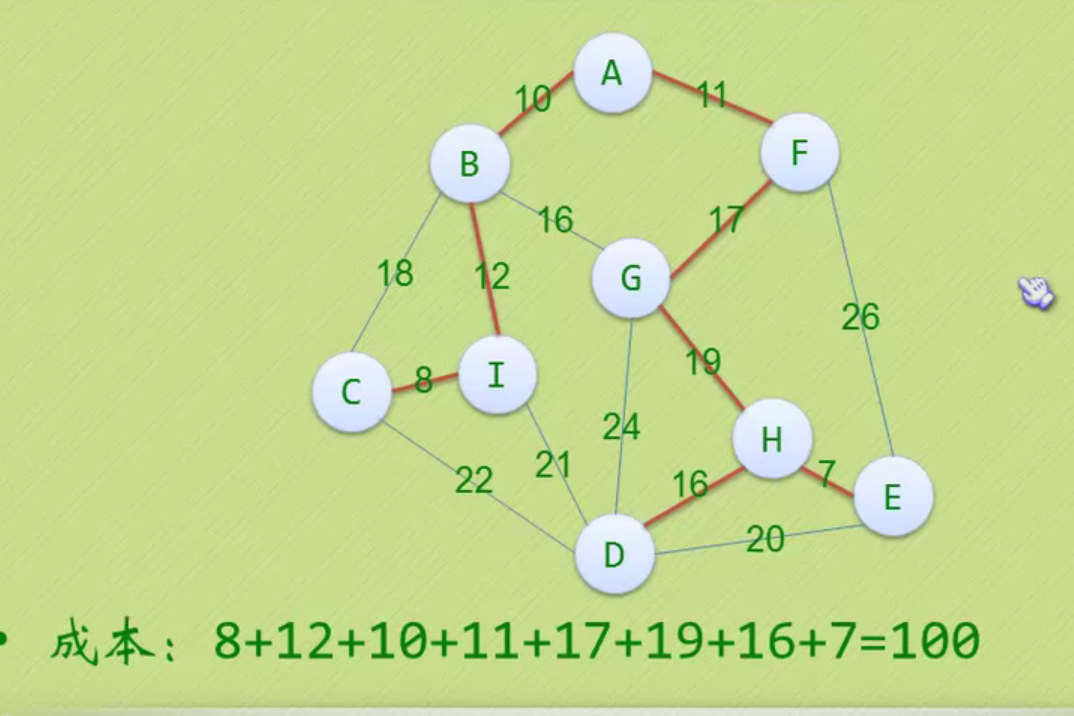
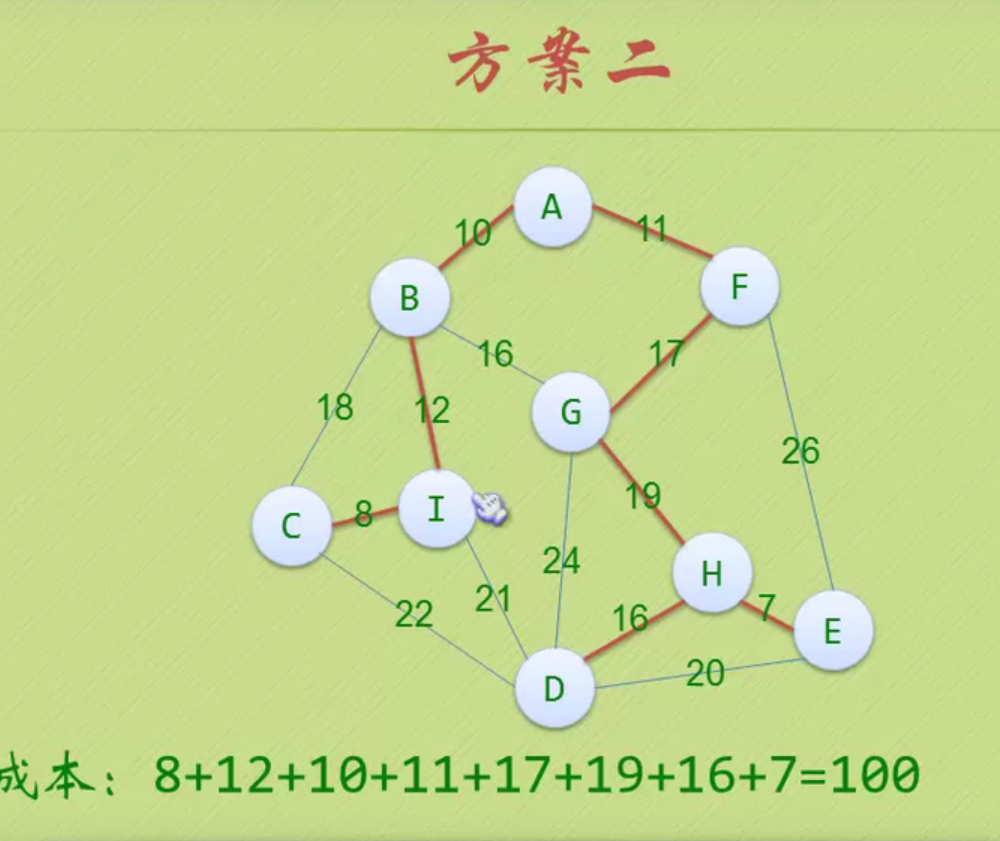
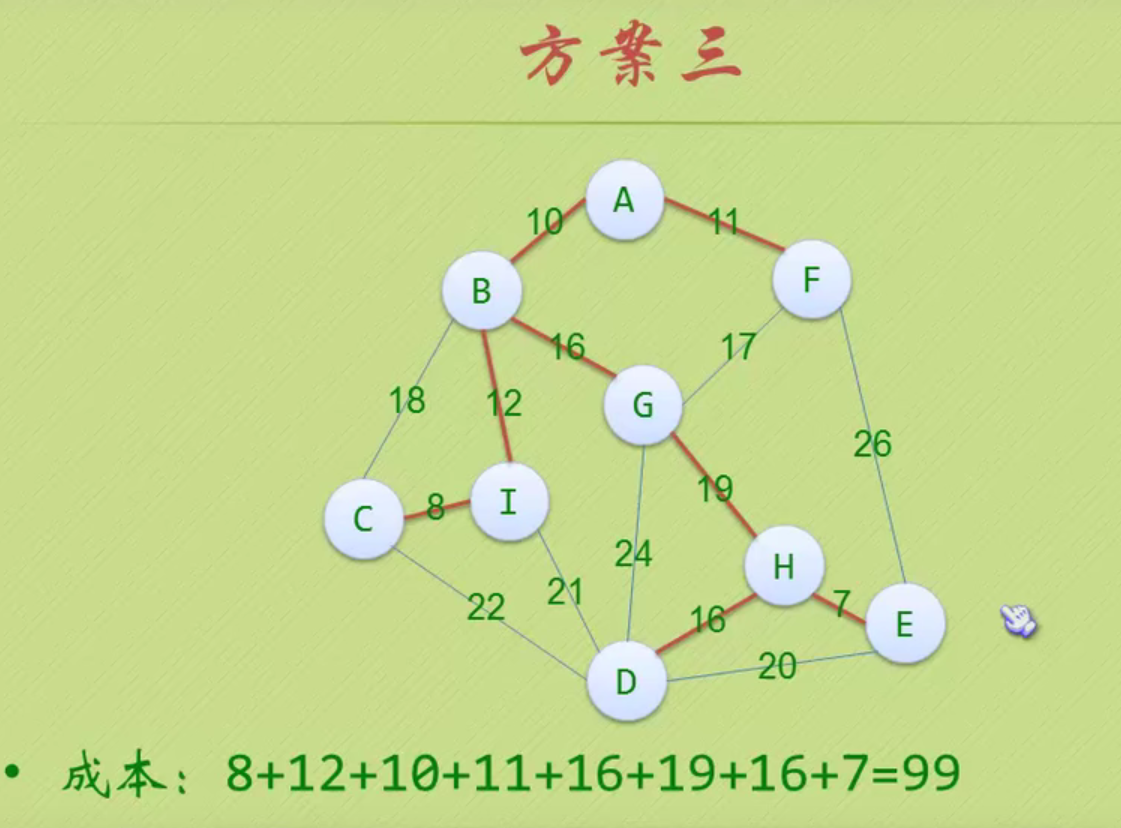
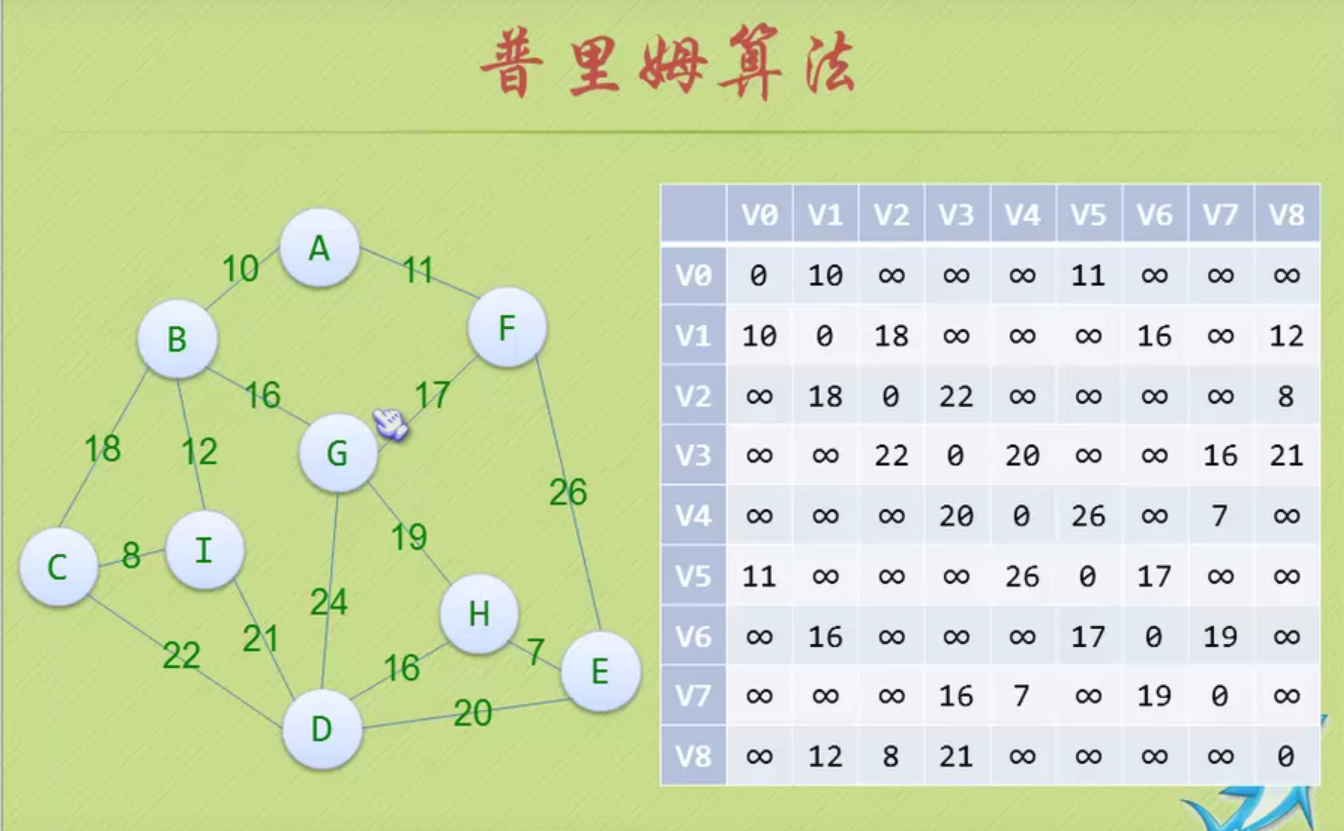
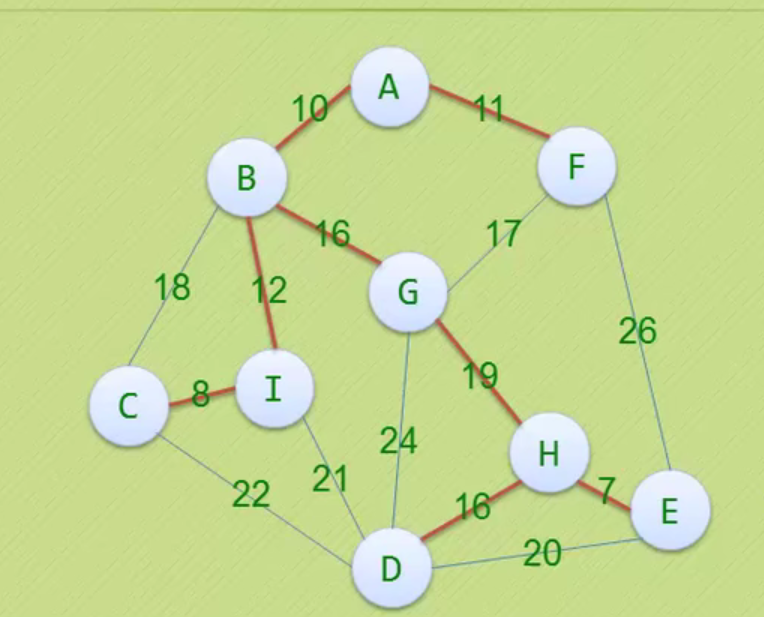
with PPT take as an example
subscript: 0 1 2 3 4 5 6 7 8
initialization: lowcost[]: 0 10 ∞ ∞ ∞ 11 ∞ ∞ ∞ -----weight
adjvex[]: 0 0 0 0 0 0 0 0 0 ------The relationship between vertices, such as: [0 0 0 1 0 0 0 1 2]Indicates that the third vertex, the seventh vertex is associated with the first vertex, and the eighth vertex is associated with the second vertex
Each cycle starts with subscript 1
--------------
First cycle:
min=10
k=1
Output:(0,1) That is( A,B)
lowcost[1]=0 express B This point has been visited.
subscript: 0 1 2 3 4 5 6 7 8
lowcost[]: 0 0 ∞ ∞ ∞ 11 ∞ ∞ ∞ -----weight
adjvex[]: 0 0 0 0 0 0 0 0 0 ------The relationship between vertices, such as: [0 0 0 1 0 0 0 1 2]Indicates that the third vertex, the seventh vertex is associated with the first vertex, and the eighth vertex is associated with the second vertex
adjacency matrix k Traverse all vertices one by one
lowcost[]: 0 0 ∞ ∞ ∞ 11 ∞ ∞ ∞ -----weight
10 0 18 ∞ ∞ ∞ 16 ∞ 12
The two compare starting with subscript 1 and assign a small value to lowcost[],meanwhile adjvex[j] = k j Representative column represents row
adjvex[]: 0 0 0 0 0 0 0 0 0 ------The relationship between vertices, such as: [0 0 0 1 0 0 0 1 2]Indicates that the third vertex, the seventh vertex is associated with the first vertex, and the eighth vertex is associated with the second vertex
to update lowcost[] adjvex[]
lowcost[]: 0 0 18 ∞ ∞ 11 16 ∞ 12 -----weight
adjvex[]: 0 0 1 0 0 0 1 0 1
--------------
--------------
Second cycle
min=11
k=5
Output: (0, 5) that is( A,F)
lowcost[5]=0 express F This point has been visited.
lowcost[]: 0 0 18 ∞ ∞ 0 16 ∞ 12 -----weight
adjvex[]: 0 0 1 0 0 0 1 0 1
adjacency matrix k Traverse all vertices one by one
lowcost[]: 0 0 18 ∞ ∞ 0 16 ∞ 12 -----weight
11 ∞ ∞ ∞ 26 0 17 ∞ ∞
The two compare starting with subscript 1 and assign a small value to lowcost[],meanwhile adjvex[j] = k j Representative column represents row
adjvex[]: 0 0 1 0 0 0 1 0 1
to update lowcost[] adjvex[]
lowcost[]: 0 0 18 ∞ 26 0 16 ∞ 12 -----weight
adjvex[]: 0 0 1 0 5 0 1 0 1
--------------
--------------
Third cycle
min=12
k=8
Output: (1, 8) that is( B,I)
lowcost[8]=0 express I This point has been visited.
lowcost[]: 0 0 18 ∞ 26 0 16 ∞ 12 -----weight
adjvex[]: 0 0 1 0 5 0 1 0 1
adjacency matrix k Traverse all vertices one by one
lowcost[]: 0 0 18 ∞ 26 0 16 ∞ 12 -----weight
∞ 12 8 21 ∞ ∞ ∞ ∞ 0
The two compare starting with subscript 1 and assign a small value to lowcost[],meanwhile adjvex[j] = k j Representative column represents row
adjvex[]: 0 0 1 0 5 0 1 0 1
to update lowcost[] adjvex[]
lowcost[]: 0 0 8 21 26 0 16 ∞ 0 -----weight
adjvex[]: 0 0 8 8 5 0 1 0 8
--------------
--------------
Fourth cycle
min=8
k=2
Output: (8, 2) that is( I,C)
lowcost[2]=0 express C This point has been visited.
lowcost[]: 0 0 8 21 26 0 16 ∞ 0 -----weight
adjvex[]: 0 0 8 8 5 0 1 0 8
adjacency matrix k Traverse all vertices one by one
lowcost[]: 0 0 8 21 26 0 16 ∞ 0 -----weight
∞ 18 0 22 ∞ ∞ ∞ ∞ 8
The two compare starting with subscript 1 and assign a small value to lowcost[],meanwhile adjvex[j] = k j Representative column represents row
adjvex[]: 0 0 8 8 5 0 1 0 8
to update lowcost[] adjvex[]
lowcost[]: 0 0 0 21 26 0 16 ∞ 0 -----weight
adjvex[]: 0 0 2 8 5 0 1 0 8
--------------
--------------
Fifth cycle
min=16
k=6
Output: (1, 6) that is( B,G)
and so on
The source code is as follows:
// Prim algorithm generates minimum spanning tree based on adjacency matrix
void MiniSpanTree_Prim(MGraph G)
{
int min, i, j, k;
int adjvex[MAXVEX]; // Save the relevant vertex subscripts. For example, [0 0 1 0 0 1 2] indicates that the third vertex, the seventh vertex is associated with the first vertex, and the eighth vertex is associated with the second vertex
int lowcost[MAXVEX]; // Save the weights of edges between related vertices
lowcost[0] = 0; // V0 starts to traverse as the root of the minimum spanning tree, and the weight is 0
adjvex[0] = 0; // V0 is the first to join
// Initialization operation
for( i=1; i < G.numVertexes; i++ )
{
lowcost[i] = G.arc[0][i]; // Add the ownership value of row 0 of adjacency matrix to the array first
adjvex[i] = 0; // Initialize all subscripts to V0 first
}
//Take PPT as an example
//So far, the value in lowcast [] is 0 10 INFINITY INFINITY INFINITY 11 INFINITY INFINITY INFINITY infinity
// The process of constructing the minimum spanning tree
for( i=1; i < G.numVertexes; i++ )
{
min = INFINITY; // The initialization minimum weight is 65535 and other impossible values
j = 1;
k = 0;
// Traverse all vertices
while( j < G.numVertexes )
{
// Find the minimum weight stored in the lowcast array
if( lowcost[j]!=0 && lowcost[j] < min )// Lowcast [J]! = 0 means you don't point to yourself
{
min = lowcost[j];//Find the smallest weight
k = j; // Store the subscript of the found minimum weight in k for use. k = 1 and k = 5
}
j++;
}
// Prints the edge with the lowest weight among the current vertex edges
printf("(%d,%d)", adjvex[k], k);//
lowcost[k] = 0; // Setting the weight of the current vertex to 0 indicates that this vertex has completed the task and traverses the next vertex
//For vertex A, the edge with the smallest weight is vertex B, so k=1
// k rows of adjacency matrix traverse all vertices one by one
//For the edges between vertices that have passed, set it to 0 to update the relationship between vertices
for( j=1; j < G.numVertexes; j++ )
{
//Compare the weight of the vertex connected with k with the weight of the vertex associated with the previous vertex
if( lowcost[j]!=0 && G.arc[k][j] < lowcost[j] )
{
lowcost[j] = G.arc[k][j];//Update the weight. Select the smallest weight. The subscript of the weight represents the label of the vertex
// This step is the most critical. Here is the principle of updating the weight. We take out the weight of the k-th vertex and other vertex edges, compare it with the original weight array, and select the smaller one to update the weight array. In order to reach the j-th vertex, it is the smallest weight
adjvex[j] = k; //Updates the connection between vertices
//Then, the updated weight array will be used in the next big cycle, and the smallest vertex will be selected. At this time, adjvex is also updated, so the k-th vertex to adjvex[k] th vertex is the minimum weight
}
}
}
}
Kruskal algorithm
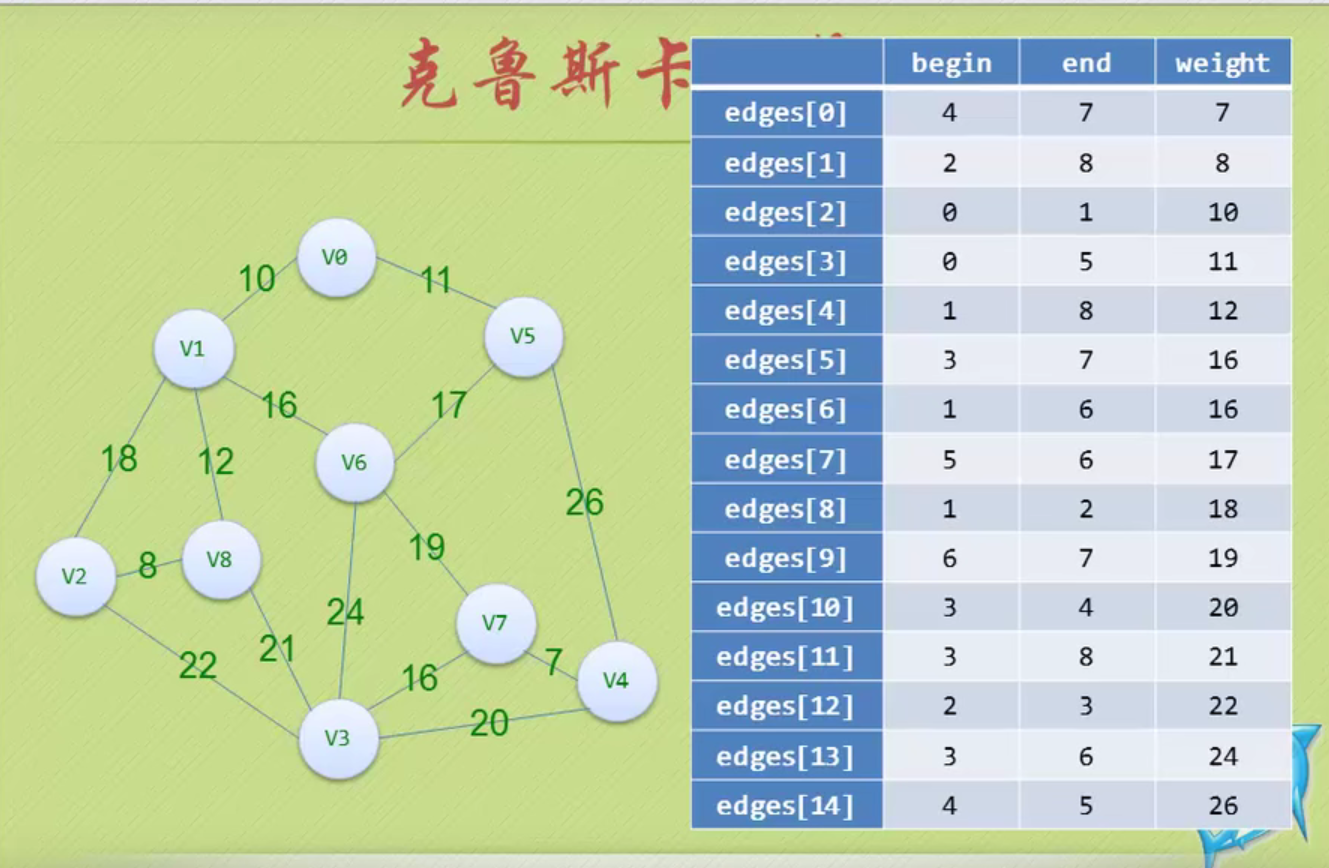
Graph structure based on edge set array
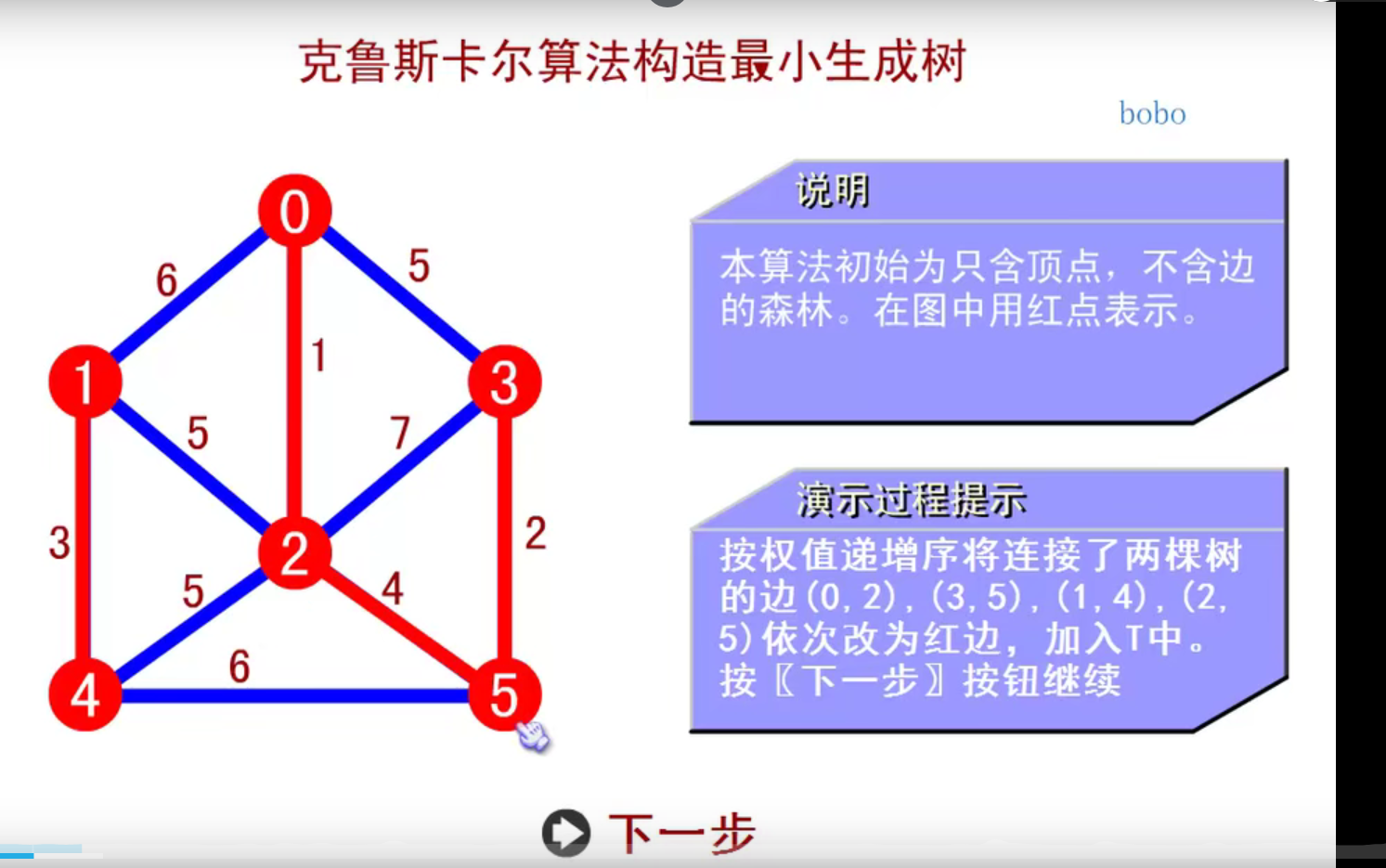
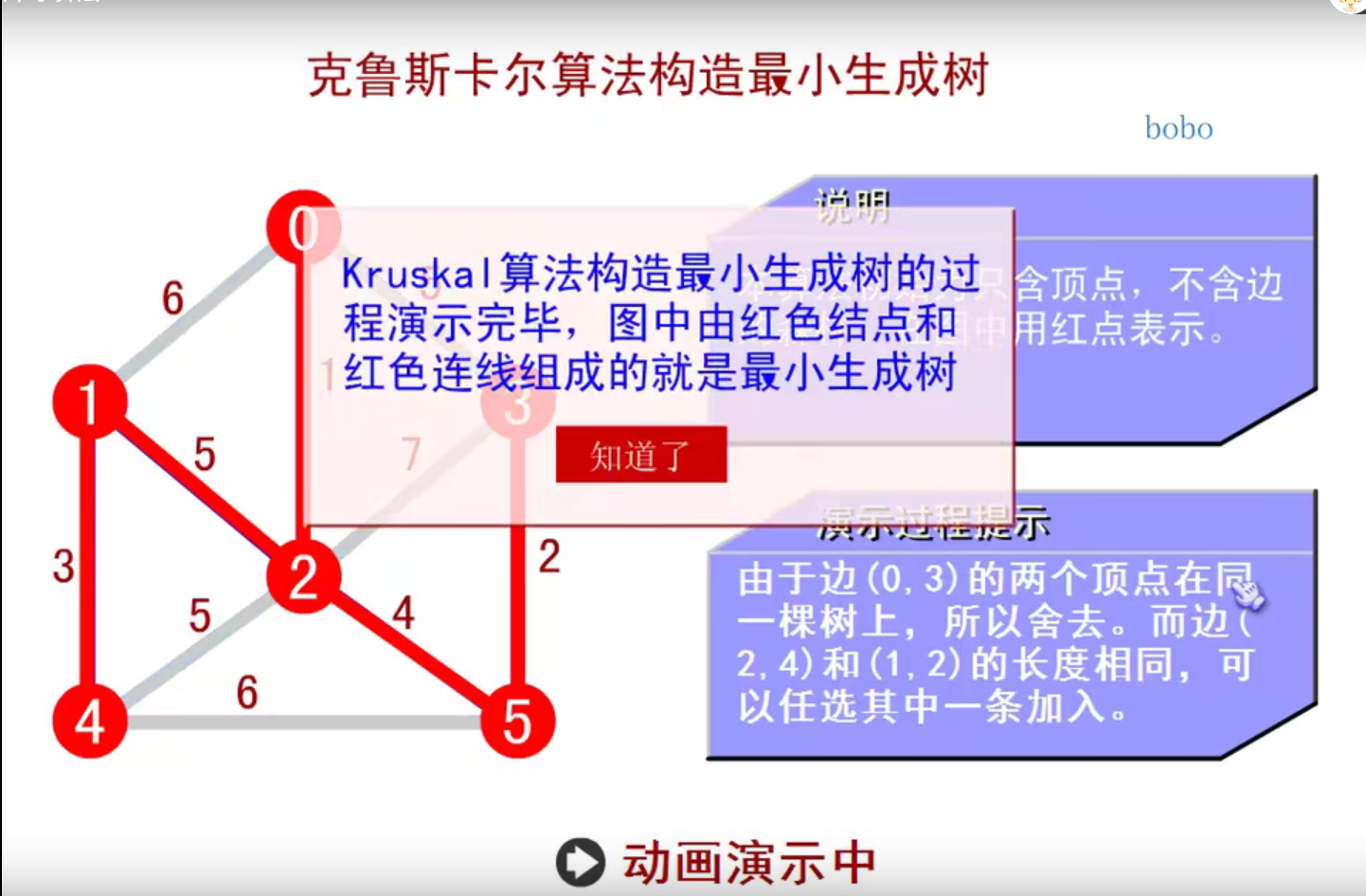
If the edge (0,3) is added, then 0,2,3,5 will form a loop, not a tree.
Similarly, just choose one of (1, 2) and (4, 2)
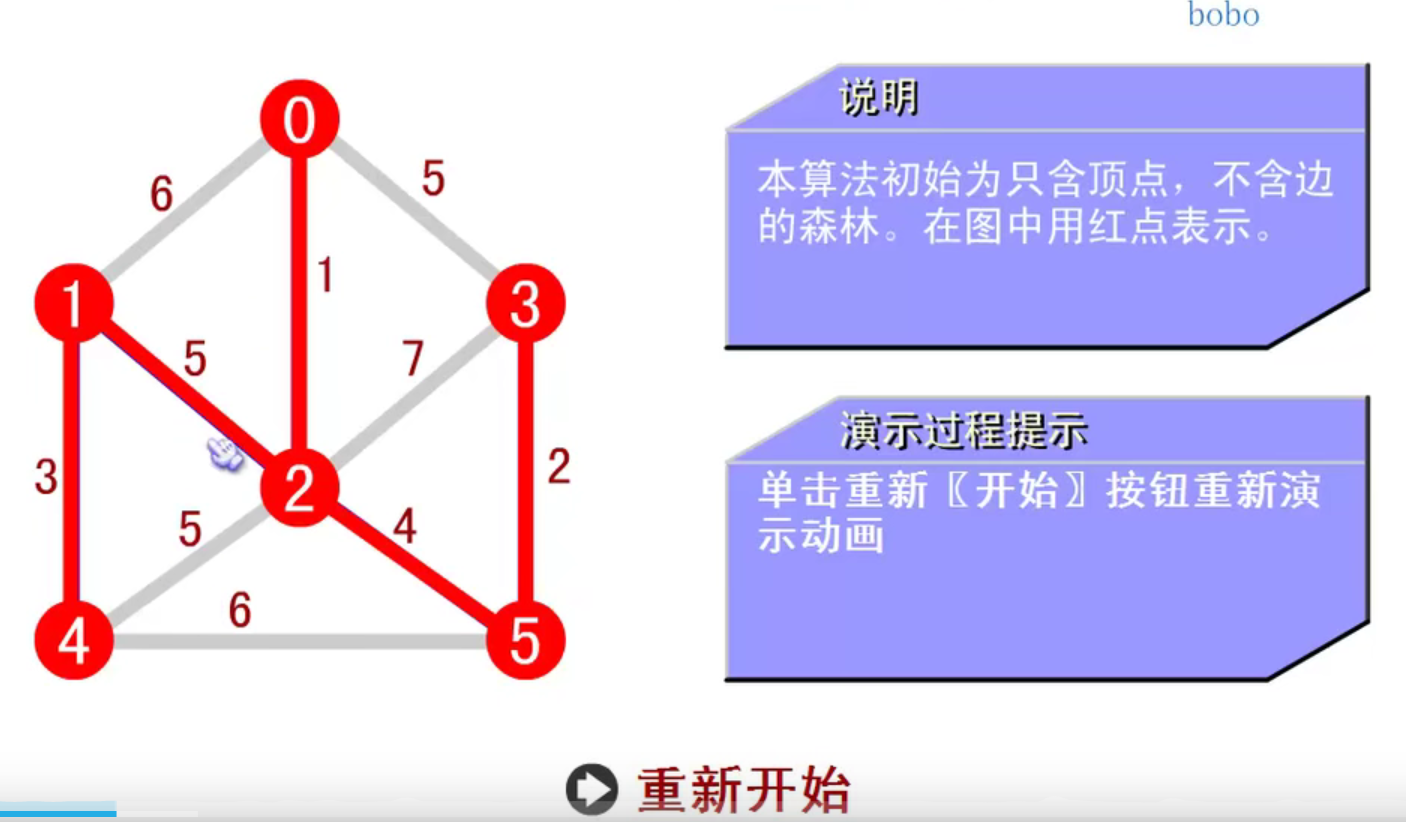
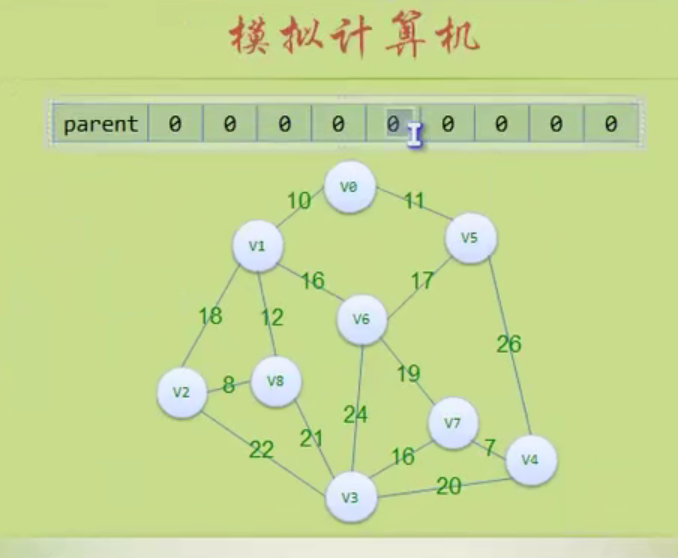
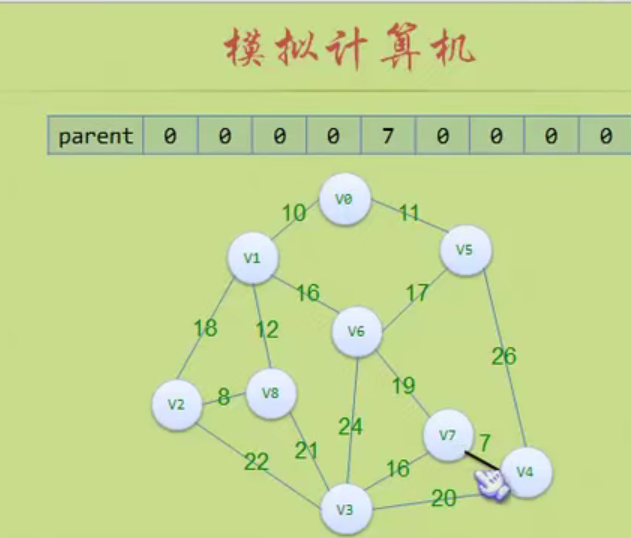
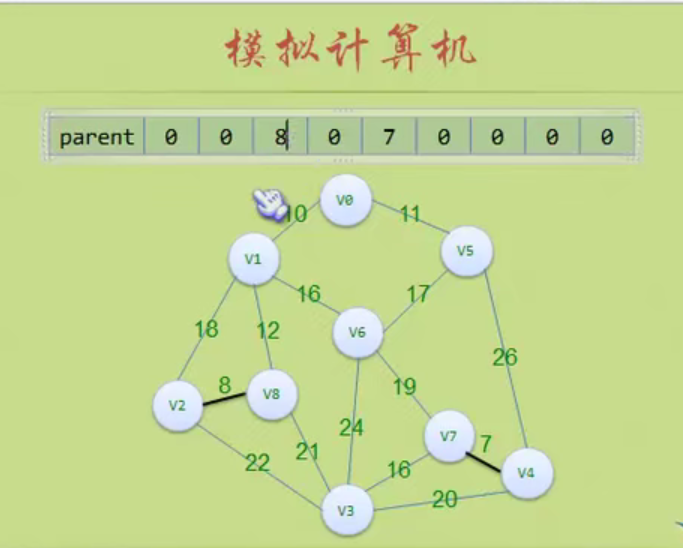
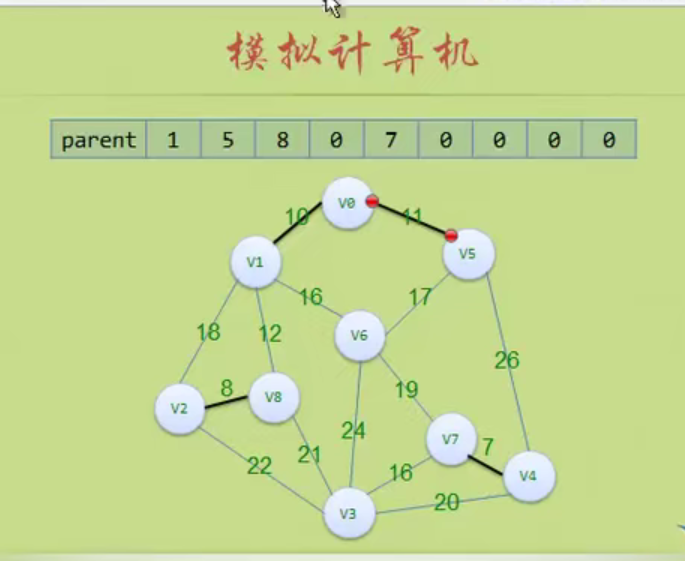
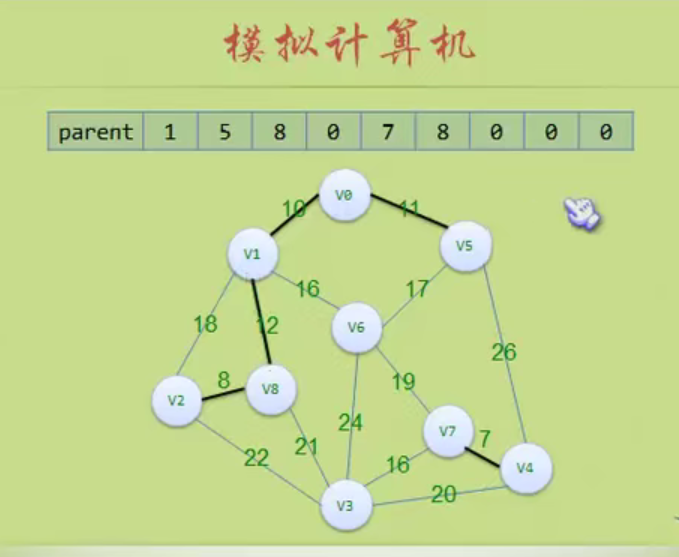
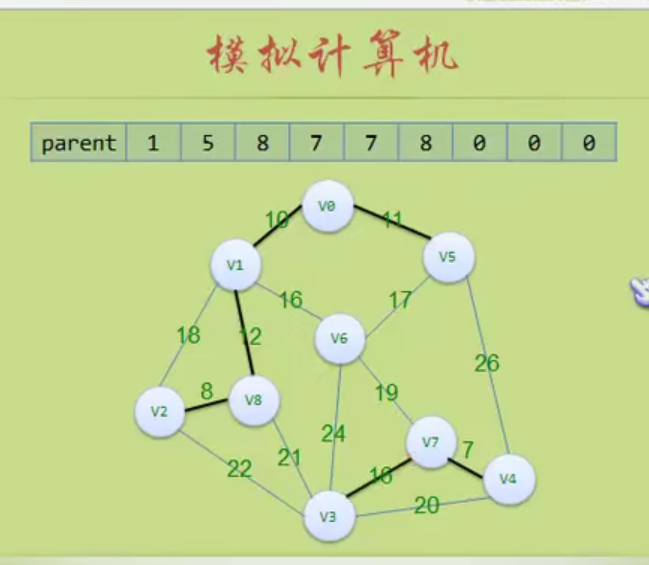
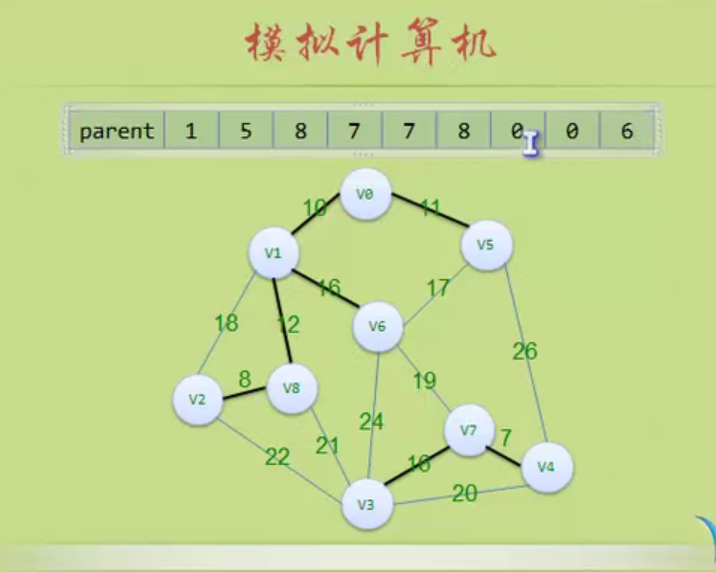
At this point, it is determined that the loop (5, 6) cannot be added
And the next (1, 2) is also determined to form a loop and cannot be added
Here we can see the function of the parent array, which actually associates the vertices of the tree.
For example (5, 6):
For 5, parent [5] = 8, parent [8] = 6, parent [6] = 0 returns 6
For 6, parent[6]=0, return 6, n==m, then form a loop, not a tree, and do not join this edge
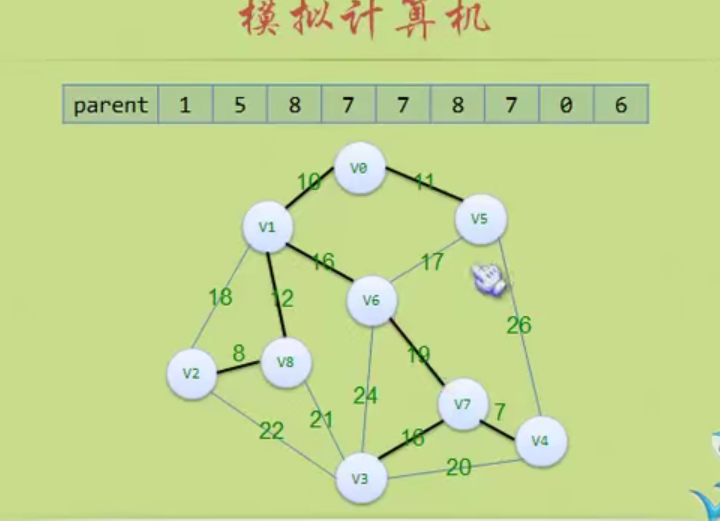
The back (3, 4) also forms a loop and does not join this side
Then the back will form a loop!
This algorithm is better understood!!! Because the edge set structure used is better understood.
For sparse graphs (that is, there are not so many edges), krukars algorithm has advantages.
For dense graphs (with fewer vertices and more edges), PRIM algorithm has advantages.
The code is as follows:
int Find(int *parent, int f)
{
while( parent[f] > 0 )
{
f = parent[f];
}
return f;
}
// Generating minimum spanning tree by Kruskal algorithm
void MiniSpanTree_Kruskal(MGraph G)
{
int i, n, m;
Edge edges[MAGEDGE]; // Define edge set array
int parent[MAXVEX]; definition parent Array is used to determine whether edges form a loop with each other
for( i=0; i < G.numVertexes; i++ )//Initialize parent
{
parent[i] = 0;
}
for( i=0; i < G.numEdges; i++ )
{
n = Find(parent, edges[i].begin); // 4 2 0 1 5 3 8 6 6 6 7
m = Find(parent, edges[i].end); // 7 8 1 5 8 7 6 6 6 7 7
if( n != m ) // If n==m, a loop is formed, which is not satisfied!
{
parent[n] = m; // Put the end vertex of this edge into the parent array with subscript as the starting point, indicating that this vertex is already in the spanning tree collection
printf("(%d, %d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
Shortest path

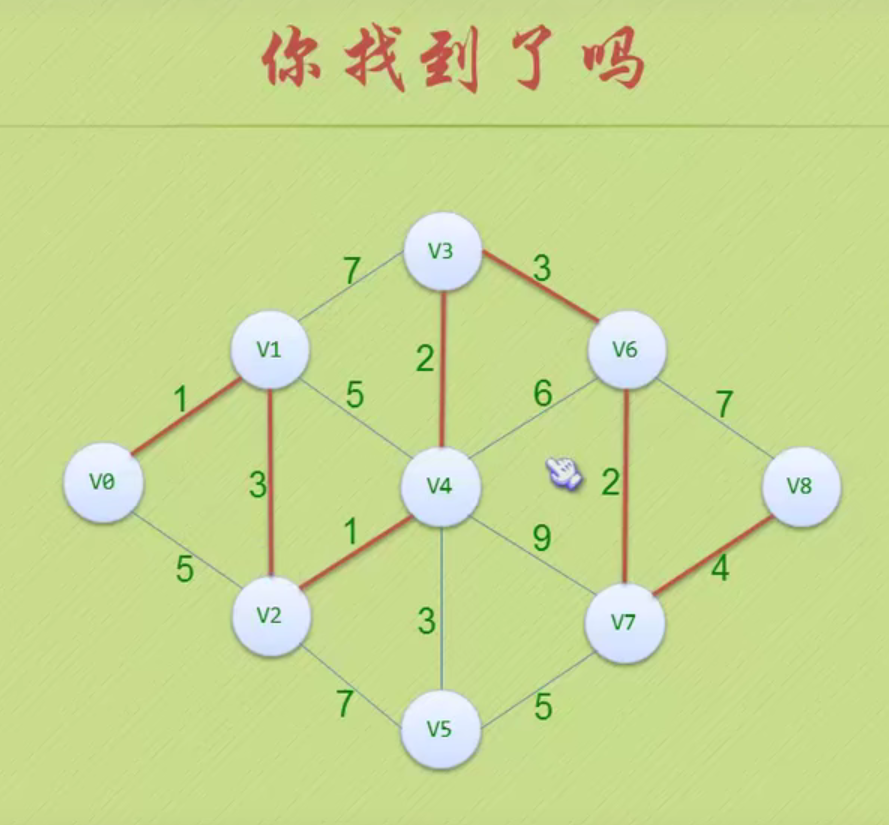
Dijestra

final[MAXVEX]; // final[w] = 1 indicates that the shortest path from vertex V0 to Vw has been obtained (*D)[w] = min + G.arc[k][w]; // Modify the current path length to store the weight and of the shortest path to each point (*p)[w] = k; // Store the precursor vertex. For example, p[2]=1 means that the precursor vertex of 2 is 1, that is, the array used to store the shortest path subscript from vertex 1 to vertex 2
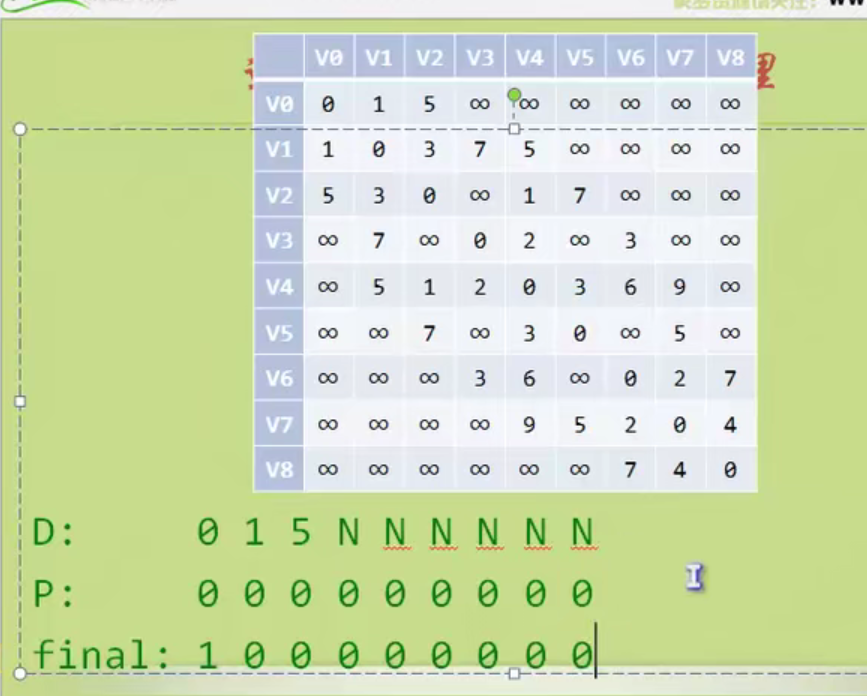


#define MAXVEX 9
#define INFINITY 65535
typedef int Patharc[MAXVEX]; // An array used to store the shortest path subscripts
typedef int ShortPathTable[MAXVEX]; // Used to store the weight sum of the shortest path to each point
void ShortestPath_Dijkstar(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
int v, w, k, min;
int final[MAXVEX]; // final[w] = 1 indicates that the shortest path from vertex V0 to Vw has been obtained
// Initialization data
for( v=0; v < G.numVertexes; v++ )
{
final[v] = 0; // All vertices initialized to the shortest path not found
(*D)[V] = G.arc[V0][v]; // Add weight to the vertex connected with V0 point
(*P)[V] = 0; // Initialize path array P to 0
}
(*D)[V0] = 0; // The path from v0 to V0 is 0
final[V0] = 1; // No path is required from V0 to V0
// Start the main loop and find the shortest path from V0 to a V vertex each time
for( v=1; v < G.numVertexes; v++ )
{
min = INFINITY;
for( w=0; w < G.numVertexes; w++ )
{
if( !final[w] && (*D)[w]<min )
{
k = w;
min = (*D)[w];
}
}
final[k] = 1; // Set the nearest vertex currently found to 1
// Correct the current shortest path and distance
for( w=0; w < G.numVextexes; w++ )
{
// If the path through v vertex is shorter than the current path, update!
if( !final[w] && (min+G.arc[k][w] < (*D)[w]) )//It's very important here. For example, when 0 goes to 1, it takes min + g.arc [k] [w] < (* d) [w]) to choose whether to go from 1 to 2 or from 0 to 2
{
(*D)[w] = min + G.arc[k][w]; // Modify the current path length
(*p)[w] = k; // Store precursor vertex
}
}
}
}
Final result
final[MAXVEX]; // final[w] = 1 indicates that the shortest path from vertex V0 to Vw has been obtained (*D)[w] = min + G.arc[k][w]; // Modify the current path length to store the weight and of the shortest path to each point (*p)[w] = k; // Store the precursor vertex. For example, p[2]=1 means that the precursor vertex of 2 is 1, that is, the array used to store the shortest path subscript from vertex 1 to vertex 2 N Represents infinity, which is 65535 in the code initialization: final: 1 0 0 0 0 0 0 0 0 D: 0 1 5 N N N N N N P: 0 0 0 0 0 0 0 0 0 from v=1 start v Represents vertex 1 **********First main cycle k=1; min=1; to update final express V0 reach Vk Shortest path found final: 1 1 0 0 0 0 0 0 0 to update D ,P D: 0 1 4 N N N N N N P: 0 0 1 0 0 0 0 0 0 **********First main cycle **********Second main cycle final: 1 1 0 0 0 0 0 0 0 D: 0 1 4 N N N N N N P: 0 0 1 0 0 0 0 0 0 k=2; min=4; to update final express V0 reach Vk Shortest path found final: 1 1 1 0 0 0 0 0 0 to update D ,P D: 0 1 4 N 5 N N N N P: 0 0 1 0 2 0 0 0 0 **********Second main cycle **********Third main cycle final: 1 1 1 0 0 0 0 0 0 D: 0 1 4 N 5 N N N N P: 0 0 1 0 2 0 0 0 0 k=4; min=5; to update final express V0 reach Vk Shortest path found final: 1 1 1 0 1 0 0 0 0 to update D ,P D: 0 1 4 7 5 N N N N P: 0 0 1 4 2 0 0 0 0 **********Third main cycle **********Fourth main cycle final: 1 1 1 0 1 0 0 0 0 D: 0 1 4 7 5 N N N N P: 0 0 1 4 2 0 0 0 0 k=3; min=7; to update final express V0 reach Vk Shortest path found final: 1 1 1 1 1 0 0 0 0 to update D ,P D: 0 1 4 7 5 N 10 N N P: 0 0 1 4 2 0 3 0 0 **********Fourth main cycle **********Fifth main cycle final: 1 1 1 1 1 0 0 0 0 D: 0 1 4 7 5 N 10 N N P: 0 0 1 4 2 0 3 0 0 k=6; min=10 to update final express V0 reach Vk Shortest path found final: 1 1 1 1 1 0 1 0 0 to update D ,P D: 0 1 4 7 5 N 10 12 N P: 0 0 1 4 2 0 3 6 0 **********Fifth main cycle **********Sixth main cycle final: 1 1 1 1 1 0 1 0 0 D: 0 1 4 7 5 N 10 12 N P: 0 0 1 4 2 0 3 6 0 k=7; min=12; to update final express V0 reach Vk Shortest path found final: 1 1 1 1 1 0 1 1 0 to update D ,P D: 0 1 4 7 5 N 10 12 16 P: 0 0 1 4 2 0 3 6 7 **********Sixth main cycle **********Seventh main cycle final: 1 1 1 1 1 0 1 1 0 D: 0 1 4 7 5 N 10 12 16 P: 0 0 1 4 2 0 3 6 7 k=8; min=14; to update final express V0 reach Vk Shortest path found final: 1 1 1 1 1 0 1 1 1 to update D ,P D: 0 1 4 7 5 N 10 12 16 P: 0 0 1 4 2 0 3 6 7 **********Seventh main cycle **********Eighth main cycle final: 1 1 1 1 1 0 1 1 1 D: 0 1 4 7 5 N 10 12 16 P: 0 0 1 4 2 0 3 6 7 **********Eighth main cycle End cycle final: 1 1 1 1 1 0 1 1 1 D: 0 1 4 7 5 N 10 12 16 P: 0 0 1 4 2 0 3 6 7 The route is 0->1->2->4->3->6->7->8
Freud

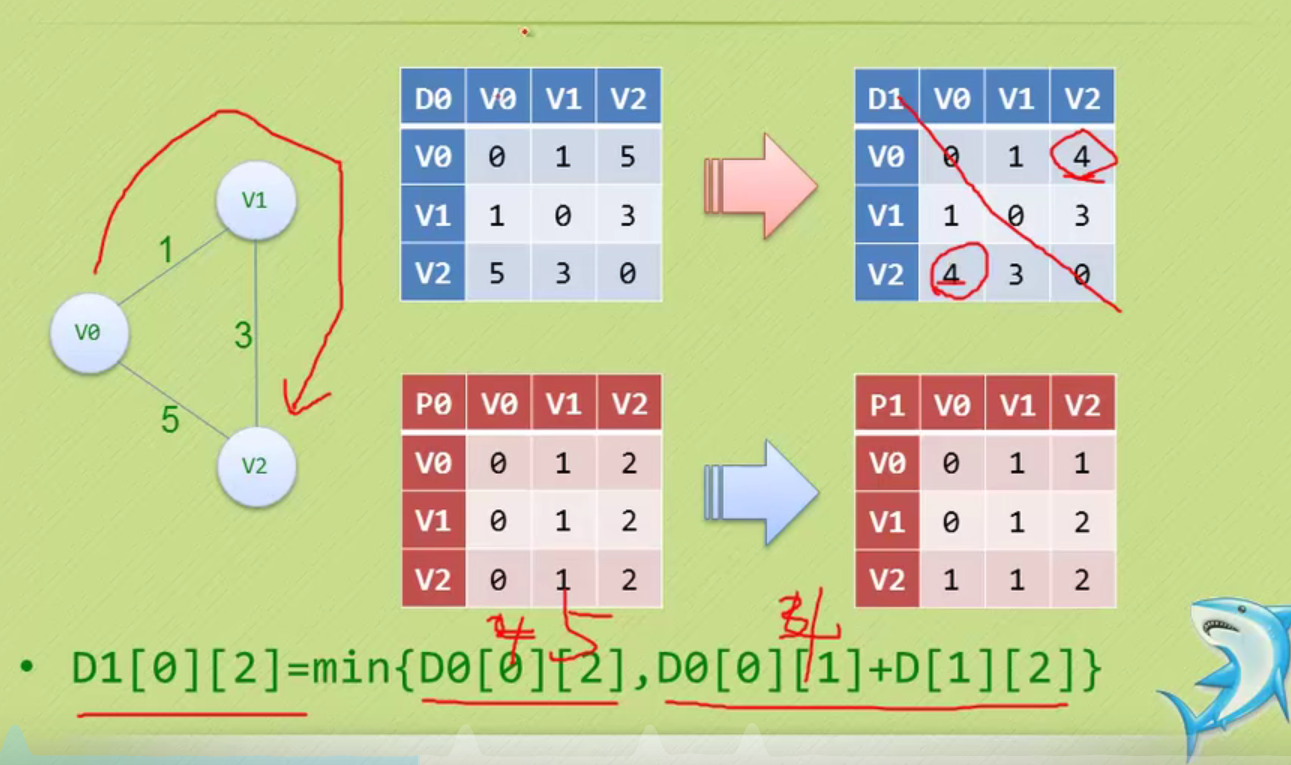
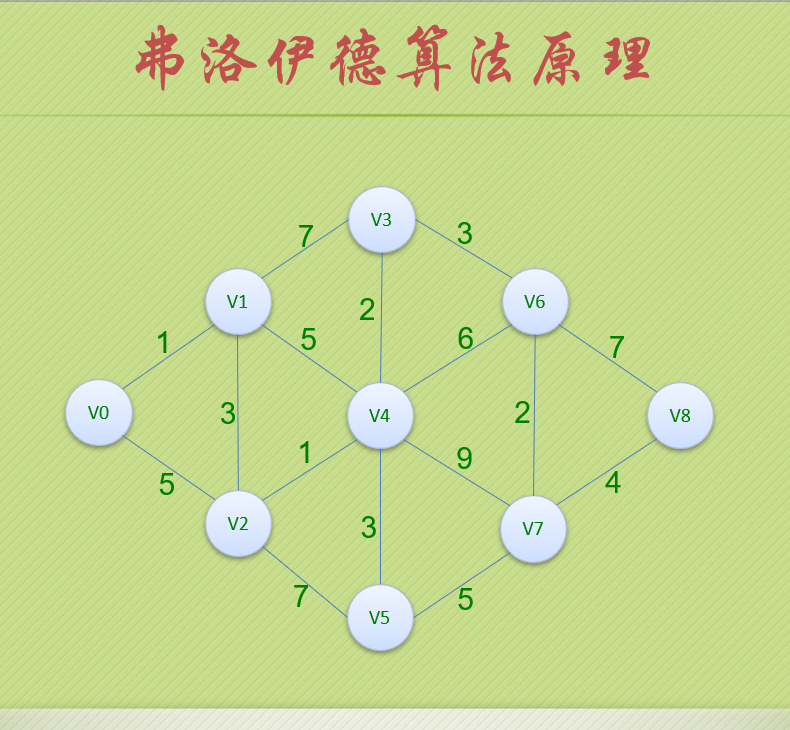
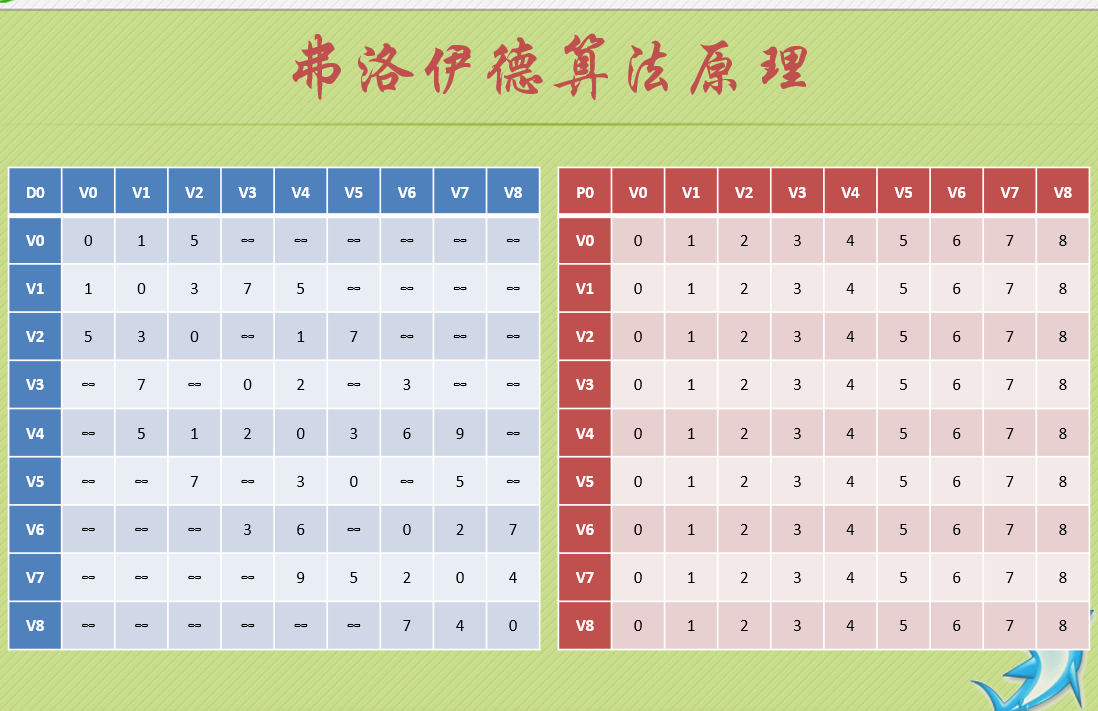
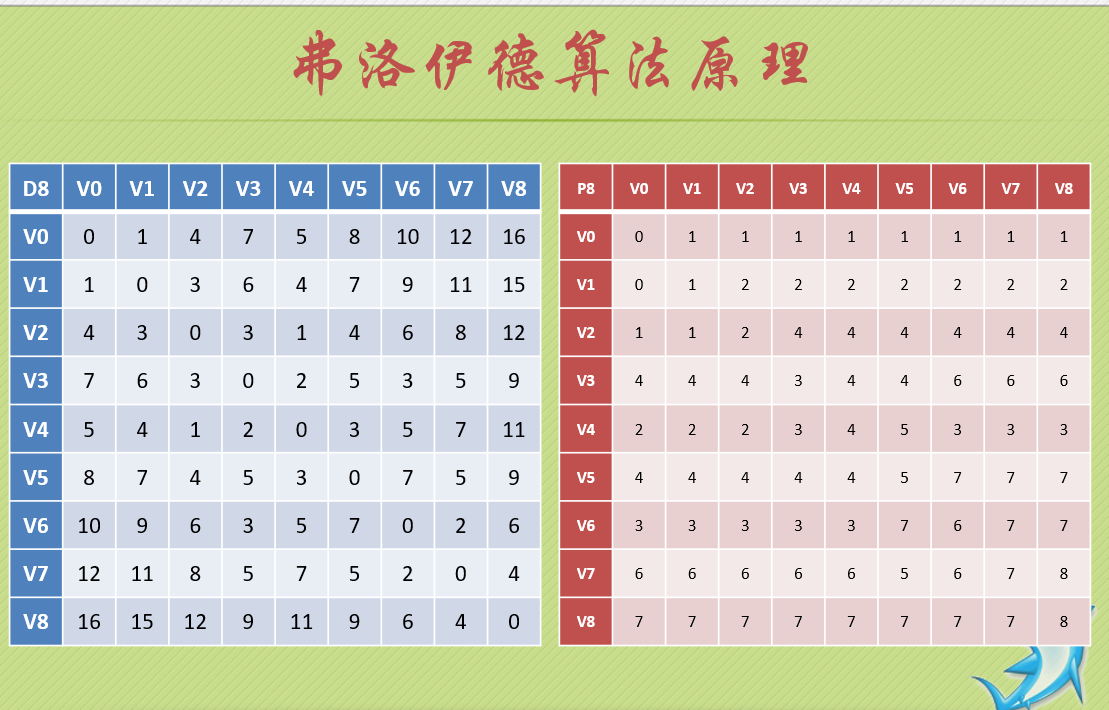
#define MAXVEX 9
#define INFINITY 65535
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
void ShortestPath_Floyd(MGraph G, Pathmatirx *P, ShortPathTable *D)
{
int v, w, k;
// Initialize D and P
for( v=0; v < G.numVertexes; v++ )
{
for( w=0; w < G.numVertexes; w++ )
{
(*D)[v][w] = G.matirx[v][w]; //Get adjacency matrix
(*P)[v][w] = w;//Initializes the precursor node between the edges
}
}
// Beautiful Freudian algorithm
//This three-layer loop takes into account all the edges and between the two
//For D arrays
//The element of D to be changed is internally controlled by two variables v,w, that is, the edge (v,w)
//For example, (0,2), that is, the route 0 - > 2, will correspond to the following situations (0,2) > (0,0) + (0,2) (0,2) > (0,1) + (1,2)
// That is, from 0 to 2, we can go like this: from 0 to 1, and then from 1 to 2
// (V, w) > (V, K) + (k, w), K plays the role of changing the route, while V, W is the vertex responsible for both ends of the edge
//For P array (* P)[v][w] = (*P)[v][k]; In other words, for the (v,w) direction, the route of (v,k) - > (k, w) can be used, so for the (v,w) W, its precursor node is k!!!
//After a three-tier cycle, all situations can be taken into account
//For example, there are several ways for 0 - > 3, 0 - > 1 + 1 - > 3
// 0->2 + 2->3 =0->1 + 1->2 + 2->4 + 4->3
// The above two cases will be taken into account, so Freud's algorithm is very simple, but the event complexity is high O (n^3)
for( k=0; k < G.numVertexes; k++ )
{
for( v=0; v < G.numVertexes; v++ )
{
for( w=0; w < G.numVertexes; w++ )
{
if( (*D)[v][w] > (*D)[v][k] + (*D)[k][w] )//Here v stands for column k
{
(*D)[v][w] = (*D)[v][k] + (*D)[k][w];
(*P)[v][w] = (*P)[v][k]; // Please think: can I change it here to (* P)[k][w]? Why?
}
}
}
}
}
Topological sorting



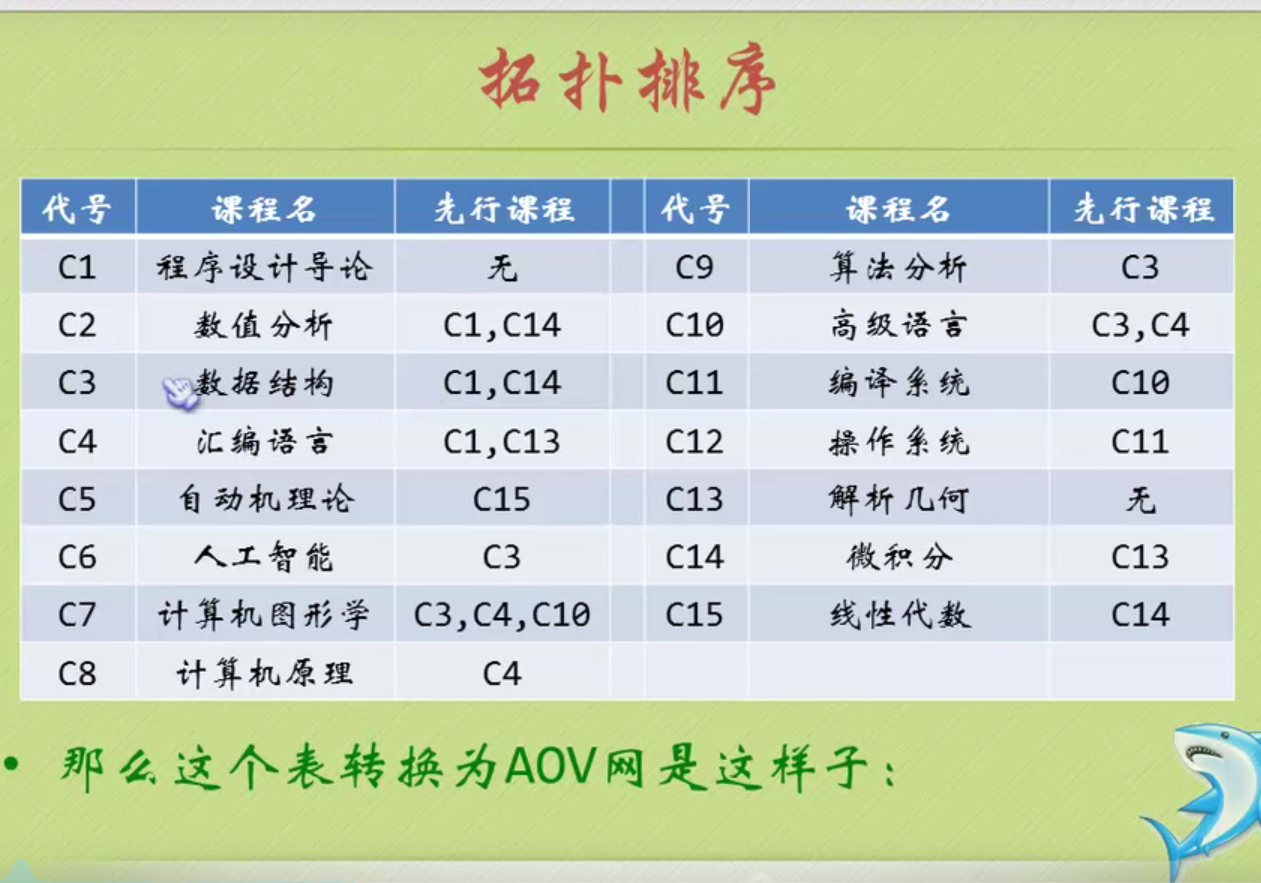
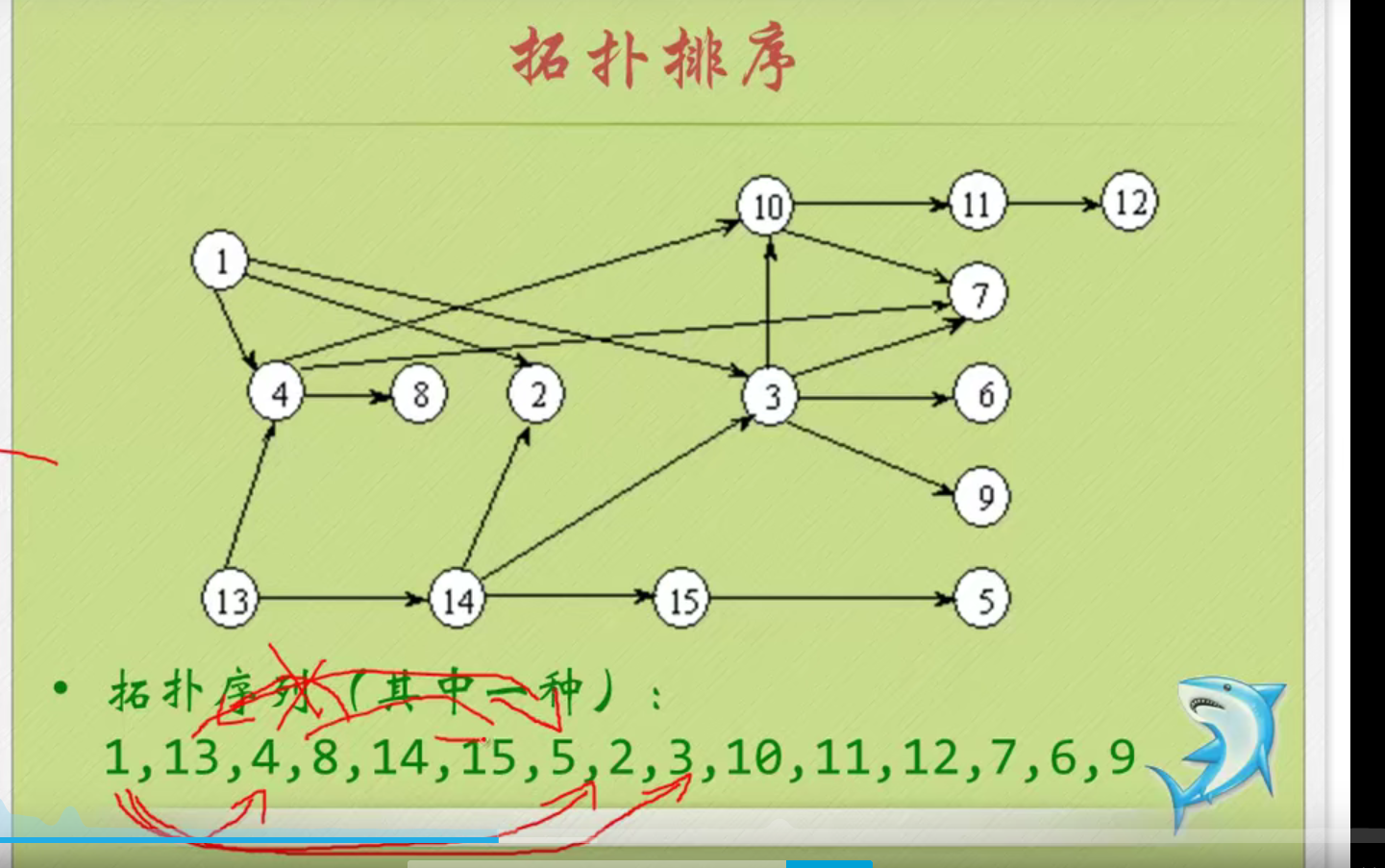
The topology must point from the front to the back

Use adjacency table
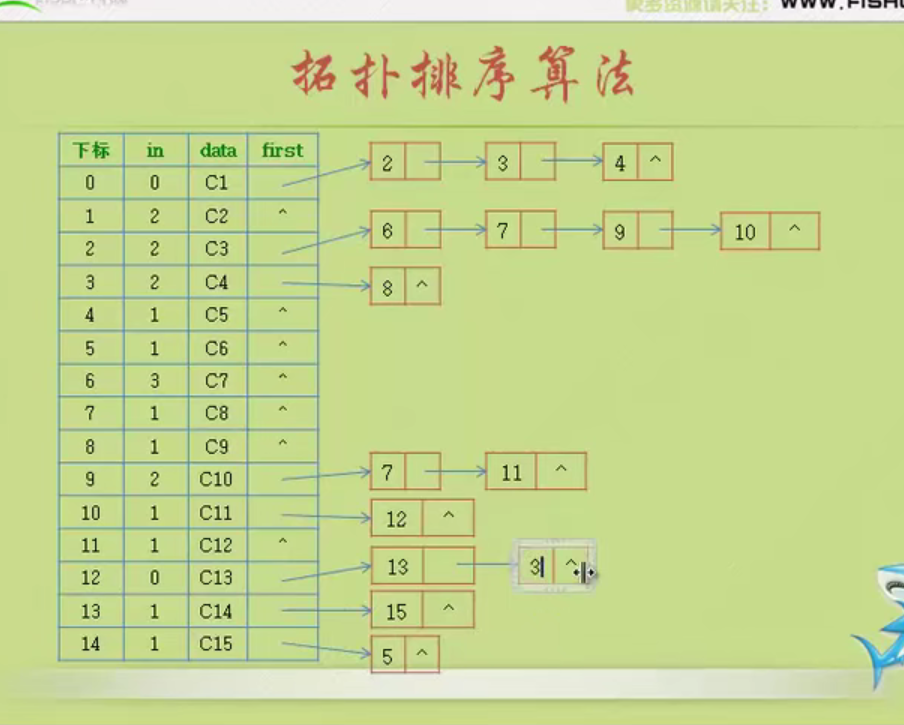

// Edge table node declaration
typedef struct EdgeNode
{
int adjvex;
struct EdgeNode *next;
}EdgeNode;
// Vertex table node declaration
//Adjacency table
typedef struct VertexNode
{
int in; // Vertex penetration
int data;
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
//Directed graph structure
typedef struct
{
AdjList adjList;
int numVertexes, numEdges;
}graphAdjList, *GraphAdjList;
// Topological sorting algorithm
// If GL has no loop, output the topology sorting sequence and return OK, otherwise return ERROR
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i, k, gettop;
int top = 0; // Index used for stack pointer subscript
int count = 0; // Used to count the number of output vertices
int *stack; // Used to store vertices with a penetration of 0
stack = (int *)malloc(GL->numVertexes * sizeof(int));
//Stack subscripts of vertices read as 0
for( i=0; i < GL->numVertexes; i++ )
{
if( 0 == GL->adjList[i].in )
{
stack[++top] = i; // Subscript vertices with a degree of 0 onto the stack
}
}
//Here top is 12
while( 0 != top )
{
gettop = stack[top--]; // Out of stack
printf("%d -> ", GL->adjList[gettop].data);
count++;
//Here is the vertex adjacent to the vertex in the traversal stack
for( e=GL->adjList[gettop].firstedge; e; e=e->next )
{
k = e->adjvex;
// Note: the following if condition is the key point of analyzing the whole program!
// Set the penetration of the adjacent contact of vertex k to - 1, because its precursor has been eliminated
// Then, judge whether the input degree after - 1 is 0. If it is 0, it will also be put on the stack
if( !(--GL->adjList[k].in) ) //Because according to the principle of the algorithm, every vertex read as zero is taken out. After it is used up, it is deleted from the graph. Therefore, its adjacent vertex penetration will be - 1 accordingly
//If the degree of GL - > adjlist [k] is 0, it will also be stacked
{
stack[++top] = k;
}
}
}
if( count < GL->numVertexes ) // If count is less than the number of vertices, there is a ring
{
return ERROR;
}
else
{
return OK;
}
}
critical path


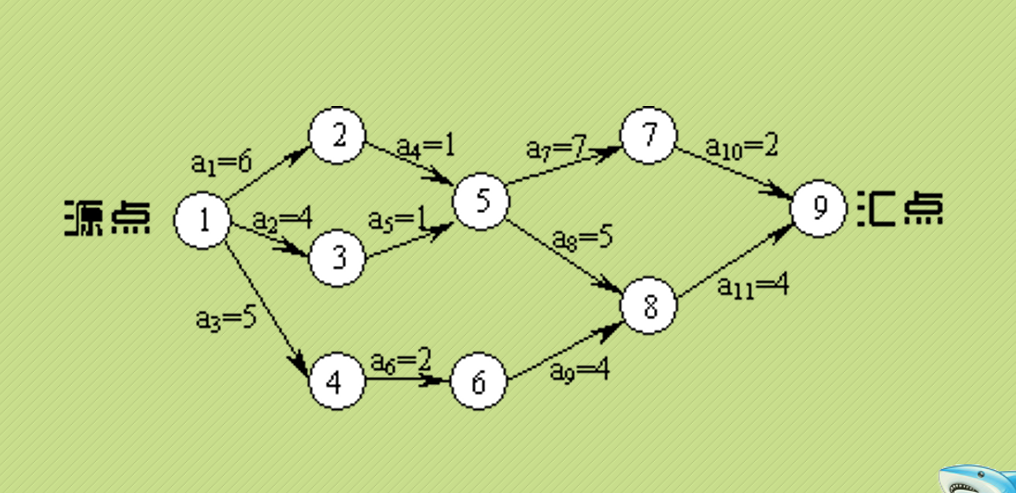
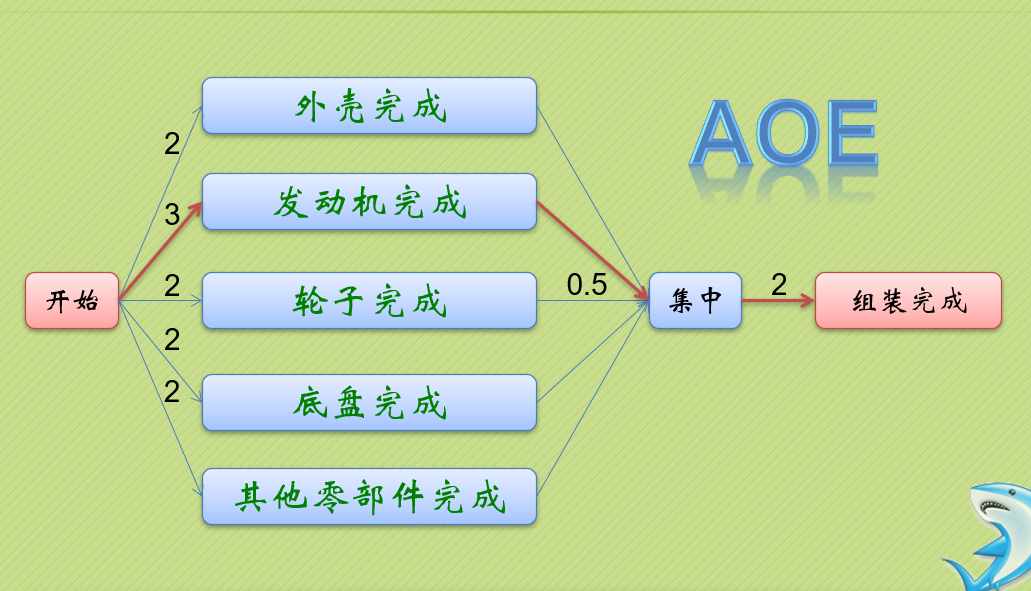


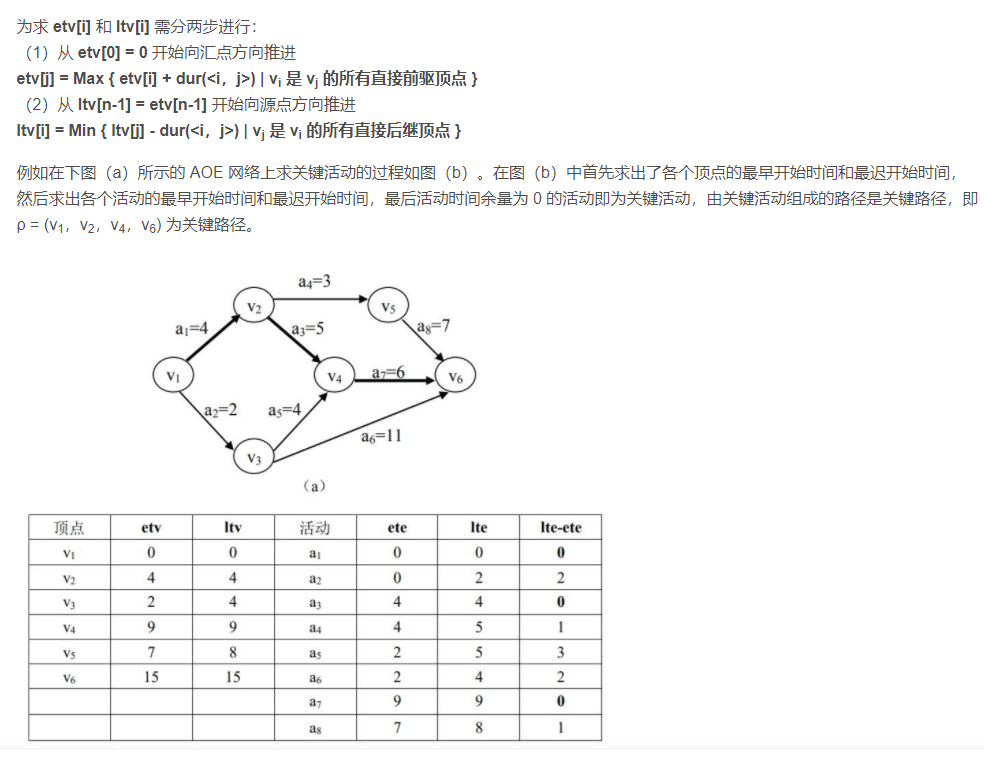

etv is pushed from left to right
ltv is pushed from right to left
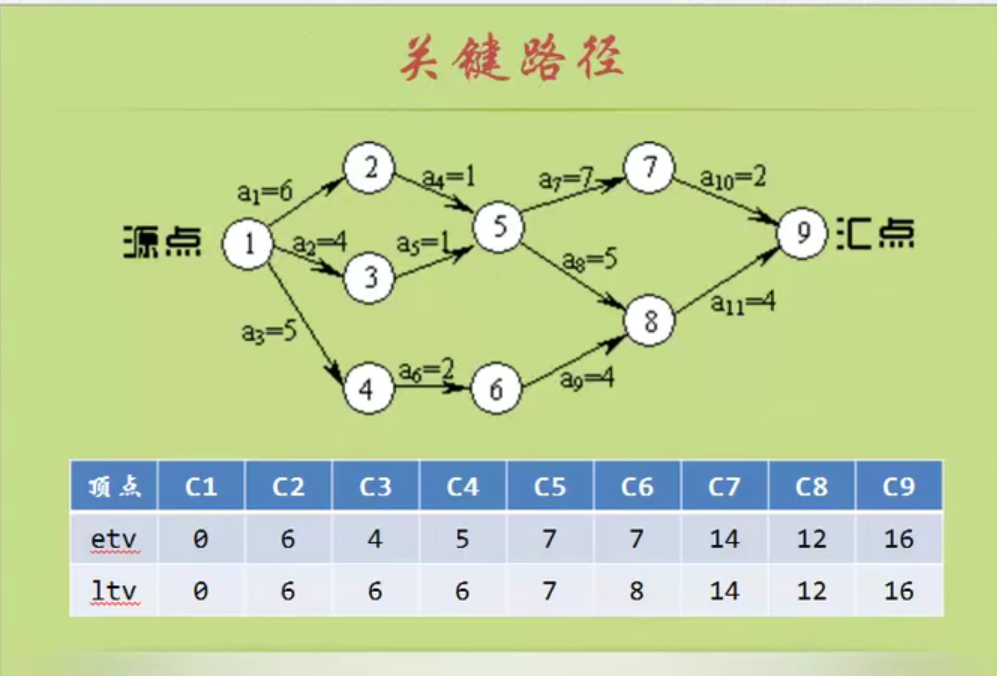
For vertices
Vertex j follows vertex i and is adjacent
Earliest occurrence time of vertex Vi + (vi,vj) weight = earliest occurrence time of vertex j
Latest occurrence time of vertex Vj - (vi,vj) weight = latest occurrence time of vertex i
For example:
For the ltv of C8, this can be understood
The latest occurrence time of C8 is 8 and the earliest occurrence time is 7, indicating that C8 can be lazy for an hour. Why? Because it takes 5 hours from vertex 5 to vertex 8, and only 4 hours from vertex 6 to vertex 8
If vertex 8 wants to start working, it must take both routes. If 5 - > 8 takes a long time, then 6 - > 8 can certainly be lazy
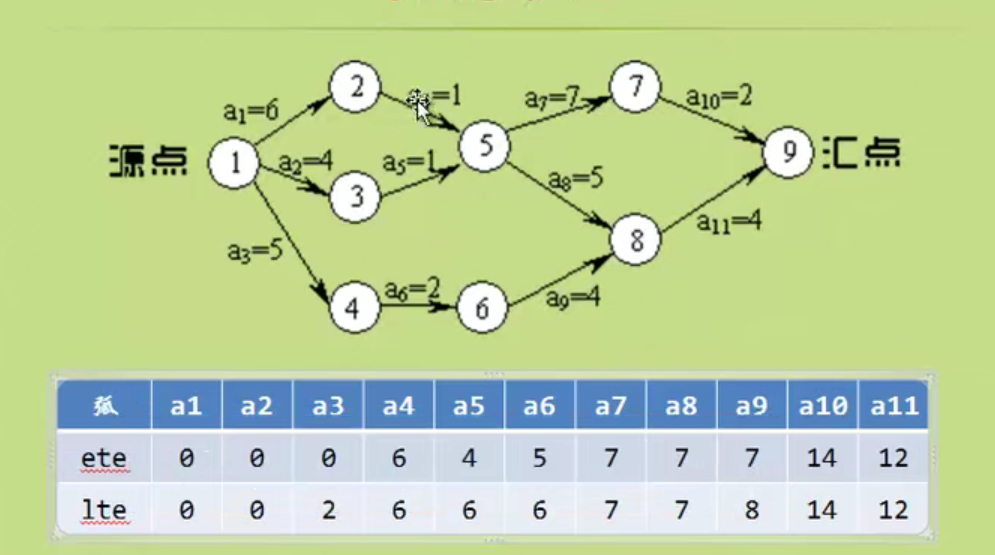
For arcs. They are the duration of time
Vertex k follows vertex j and is adjacent
Earliest occurrence time of arc between vertex k and vertex j = earliest occurrence time of vertex j
The latest occurrence time of the arc between vertex k and vertex j = the latest occurrence time of vertex k - the weight between vertex k and vertex j
For example:
For arc a4, the earliest occurrence time of ete is the earliest occurrence time etv of vertex C2.
lte is also pushed from right to left. For example, the latest occurrence time of a11 and a11 lte = the latest occurrence time of vertex C9 – 4 = 16-4 = 12, and so on.
Summary:
For vertices:
vertex j At vertex i Behind and adjacent
vertex Vi Earliest occurrence time of +(vi,vj)Right of = vertex j Earliest occurrence time of
vertex Vj Latest occurrence time of -(vi,vj)Right of = vertex i Latest occurrence time of
For arcs. They are the duration of time:
vertex k At vertex j Behind and adjacent
vertex k And vertex j Earliest occurrence time of arc between=vertex j Earliest occurrence time of
vertex k And vertex j Latest occurrence time of arc between= vertex k Latest occurrence time of- vertex k And vertex j Right between
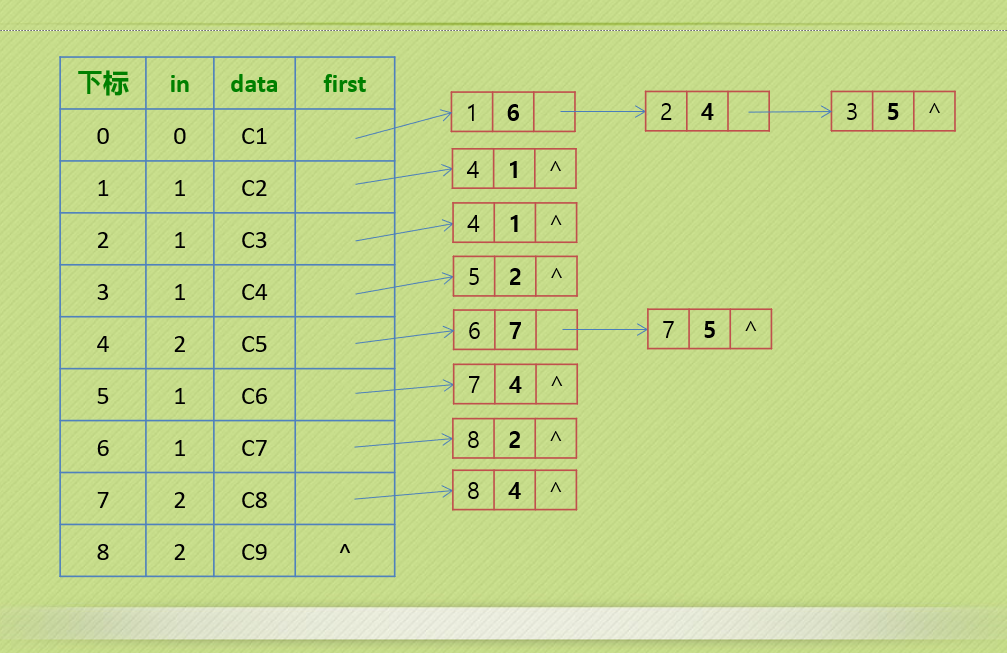
// Edge table node declaration
typedef struct EdgeNode
{
int adjvex;
struct EdgeNode *next;
}EdgeNode;
// Vertex table node declaration
typedef struct VertexNode
{
int in; // Vertex penetration
int data;
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes, numEdges;
}graphAdjList, *GraphAdjList;
int *etv, *ltv;
int *stack2; // Stack for storing topological sequences
int top2; // Stack top pointer for stack2
// Topological sorting algorithm
// If GL has no loop, output the topology sorting sequence and return OK, otherwise return ERROR
/**
* The topological order is obtained, and the etv is obtained
* @param GL
* @return
*/
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i, k, gettop;
int top = 0; // Index used for stack pointer subscript
int count = 0; // Used to count the number of output vertices
int *stack; // Used to store vertices with a penetration of 0
stack = (int *)malloc(GL->numVertexes * sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
if( 0 == GL->adjList[i].in )
{
stack[++top] = i; // Subscript vertices with a degree of 0 onto the stack
}
}
// Initialization etv is 0
top2 = 0;
etv = (int *)malloc(GL->numVertexes*sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
etv[i] = 0;
}
stack2 = (int *)malloc(GL->numVertexes*sizeof(int));
while( 0 != top )
{
gettop = stack[top--]; // Out of stack
// printf("%d -> ", GL->adjList[gettop].data);
stack2[++top2] = gettop; // Save topology sequence order C1 C2 C3 C4.... C9
count++;
for( e=GL->adjList[gettop].firstedge; e; e=e->next )
{
k = e->adjvex;//k is the adjacent vertex
// Note: the following if condition is the key point of analyzing the whole program!
// Set the penetration of the adjacent contact of vertex k to - 1, because its precursor has been eliminated
// Then, judge whether the input degree after - 1 is 0. If it is 0, it will also be put on the stack
//Here is topological sorting
if( !(--GL->adjList[k].in) )
{
stack[++top] = k;
}
//
if( (etv[gettop]+e->weight) > etv[k] )//This step is very important. It is used to calculate the earliest occurrence time of vertices. It is better to understand it according to the picture of PPT
//A large value is the earliest occurrence time of vertex k, which is equivalent to the earliest occurrence time of vertex Vi + (vi,vj) weight = the earliest occurrence time of vertex j
{
etv[k] = etv[gettop] + e->weight;
}
}
}
if( count < GL->numVertexes ) // If count is less than the number of vertices, there is a ring
{
return ERROR;
}
else
{
return OK;
}
}
// Find the critical path, GL is a directed graph, and output the key activities of GL
void CriticalPath(GraphAdjList GL)
{
EdgeNode *e;
int i, gettop, k, j;
int ete, lte;
// Call the improved topology sorting to find the values of etv and stack2
TopologicalSort(GL);
// Time to initialize ltv to sink
ltv = (int *)malloc(GL->numVertexes*sizeof(int));
for( i=0; i < GL->numVertexes; i++ )
{
ltv[i] = etv[GL->numVertexes-1];
}
// Calculate ltv one by one from the sink
while( 0 != top2 )
{
gettop = stack2[top2--]; // Note that the first out of the stack is the sink. The first out of the stack sink is actually useless because its first edge points to null
//When it comes to C8, the real calculation begins
for( e=GL->adjList[gettop].firstedge; e; e=e->next )
{
k = e->adjvex;
if( (ltv[k] - e->weight) < ltv[gettop] )//Here you need to fill in a small one. In order not to delay the construction period, you can understand the code from the ltv of the source point
{
ltv[gettop] = ltv[k] - e->weight;//The latest occurrence time of vertex gettop = the latest occurrence time of vertex k - the weight between vertex gettop and vertex k
}
}
}
// Find ete and lte through etv and ltv
for( j=0; j < GL->numVertexes; j++ )
{
//Traverse the left and right adjacent vertices of vertices
for( e=GL->adjList[j].firstedge; e; e=e->next )
{
k = e->adjvex;//Get adjacent vertices
ete = etv[j];//The earliest occurrence time of the arc between ete vertex k and vertex j = the earliest occurrence time of vertex j
lte = ltv[k] - e->weight;//The latest occurrence time of the arc between lte vertex k and vertex j = the latest occurrence time of vertex k - the weight between vertex k and vertex j
if( ete == lte )//Print if ete equals lte
{
printf("<v%d,v%d> length: %d , ", GL->adjList[j].data, GL->adjList[k].data, e->weight );
}
}
}
}
Final result
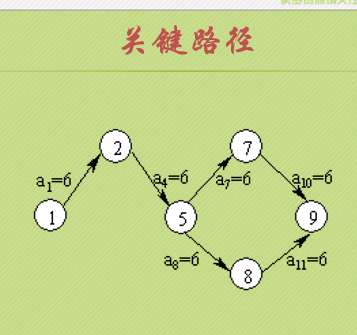
Search algorithm
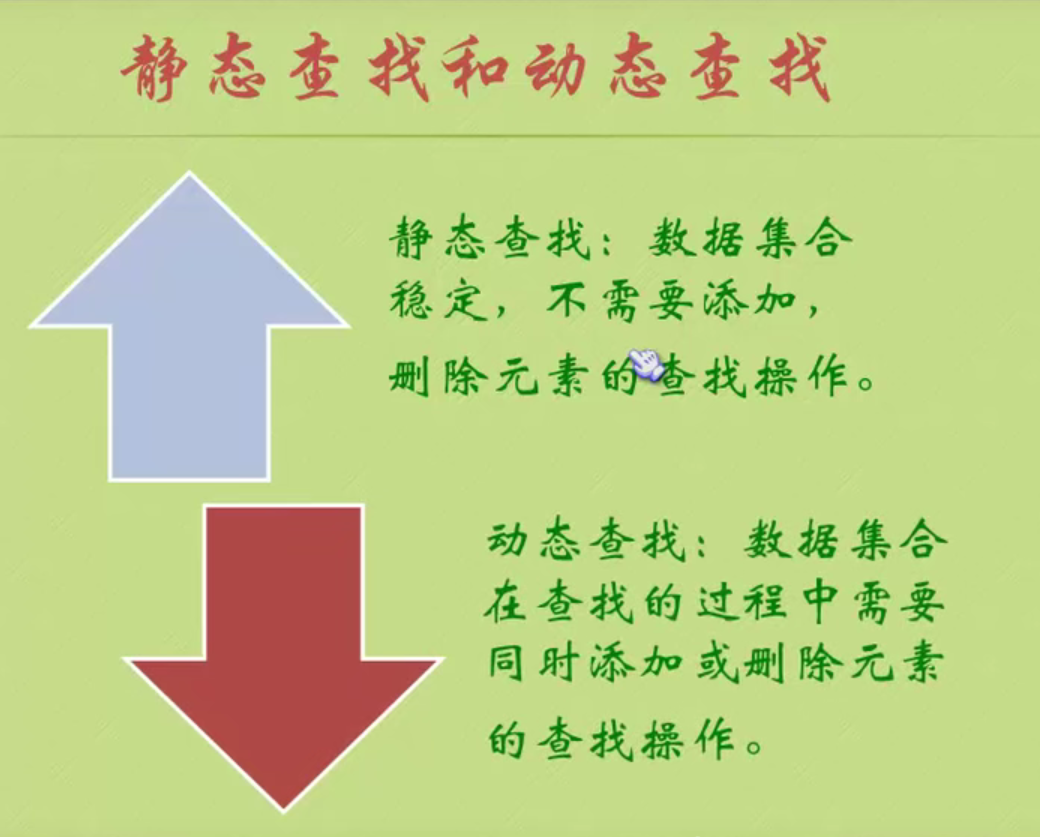

Sequential search

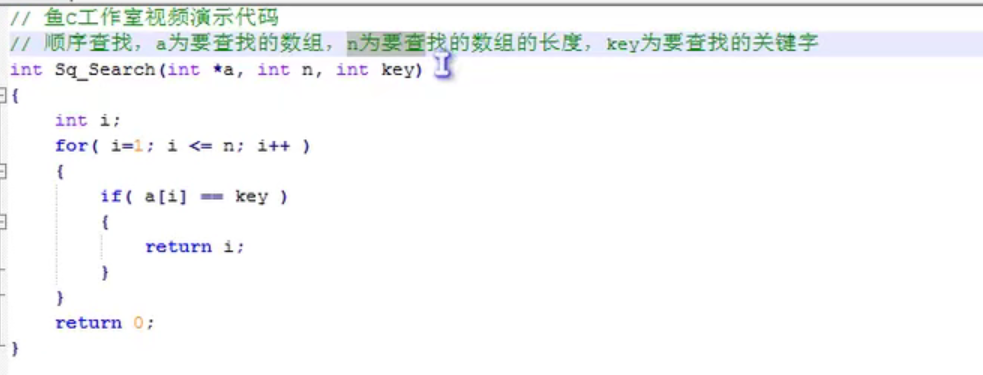
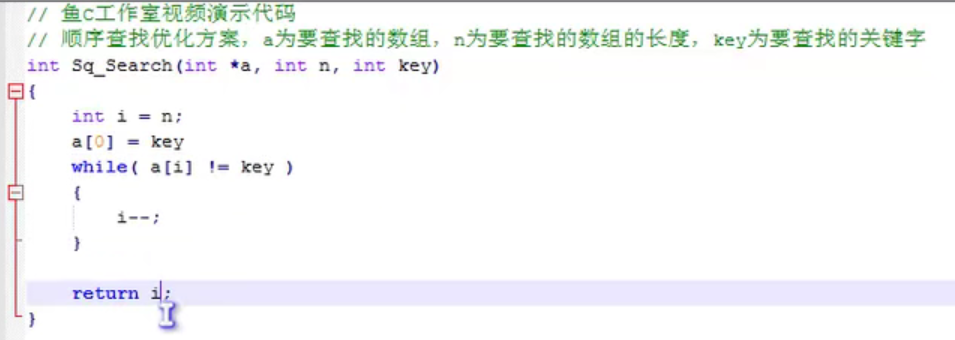
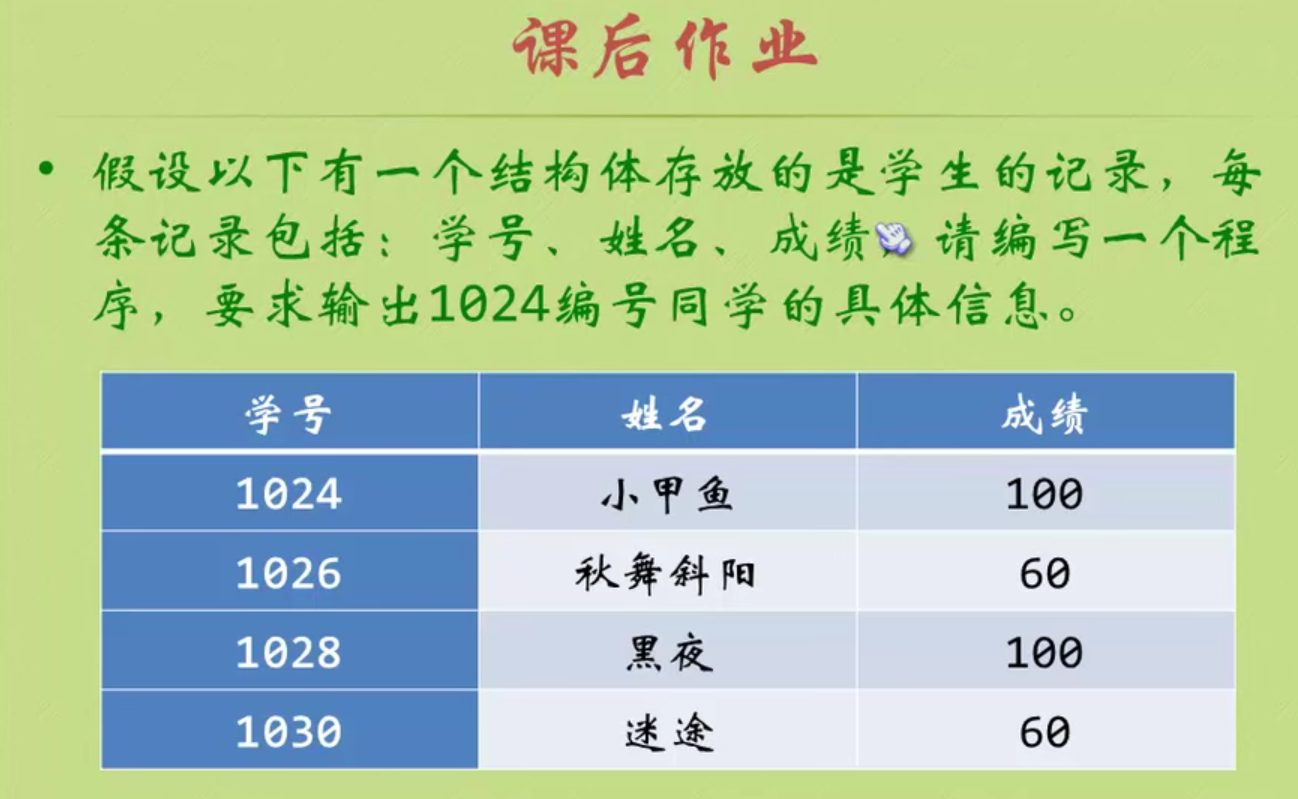
Half search


Interpolation lookup (find by scale)
Interpolation is to use the scale to get the closest position.
The time complexity of interpolation method and half method is O(log2n).
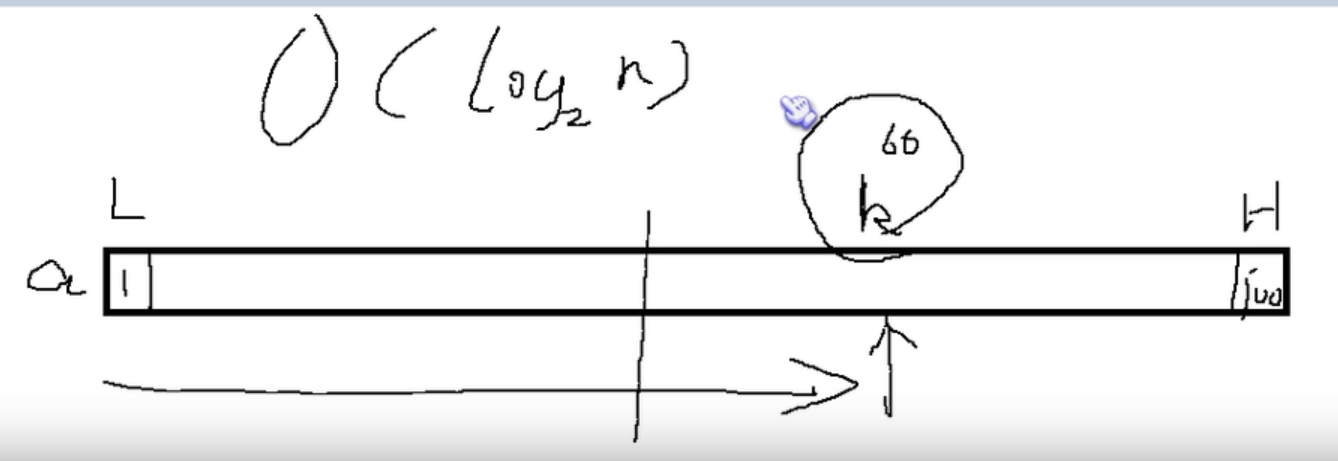
On average, the performance of interpolation method is higher than that of half method
However, if the data growth is extremely uneven, such as from 1 to 1000 to 10000 to 100000000, the efficiency of the interpolation method will not work at this time, because its proportion is meaningless
Fibonacci search (golden ratio search)



//We can see from the code
//In fact, it uses the golden ratio to locate mid
//Conditions: (1) data must adopt sequential storage structure; (2) The data must be in order.
//Principle: (1) the Fibonacci value closest to the search length is used to determine the split point; (2) Golden section.
int Fibonacci_Search(int *a,int n,int key)
{
int low,high,mid,i,k;
low=1;
high=n;//Maximum subscript of a array
k=0;
while(n>F[k]-1)//Calculate the weizhi of n in Fibonacci sequence
{
k++;
}
for(i=n;i<F[k]-1;i++)//Complete the dissatisfied value
{
a[i]=a[n];
}
while(low<=high)
{
mid=low+F[k-1]-1;//Calculates the subscript of the current separator
if(key<a[mid])//
{
high=mid-1;//Adjust highest subscript
k=k-1;//Fibonacci sequence subscript-1
}
else if(key>a[mid])
{
low=mid+1;//Adjust lowest subscript
k=k-2;//Fibonacci sequence subscript-2
}
else//equal
{
if(mid<=n)
return mid;
else//If mid > n indicates an incomplete value, n is returned
return n;
}
}
return 0;
}




Linear index lookup
Dense index
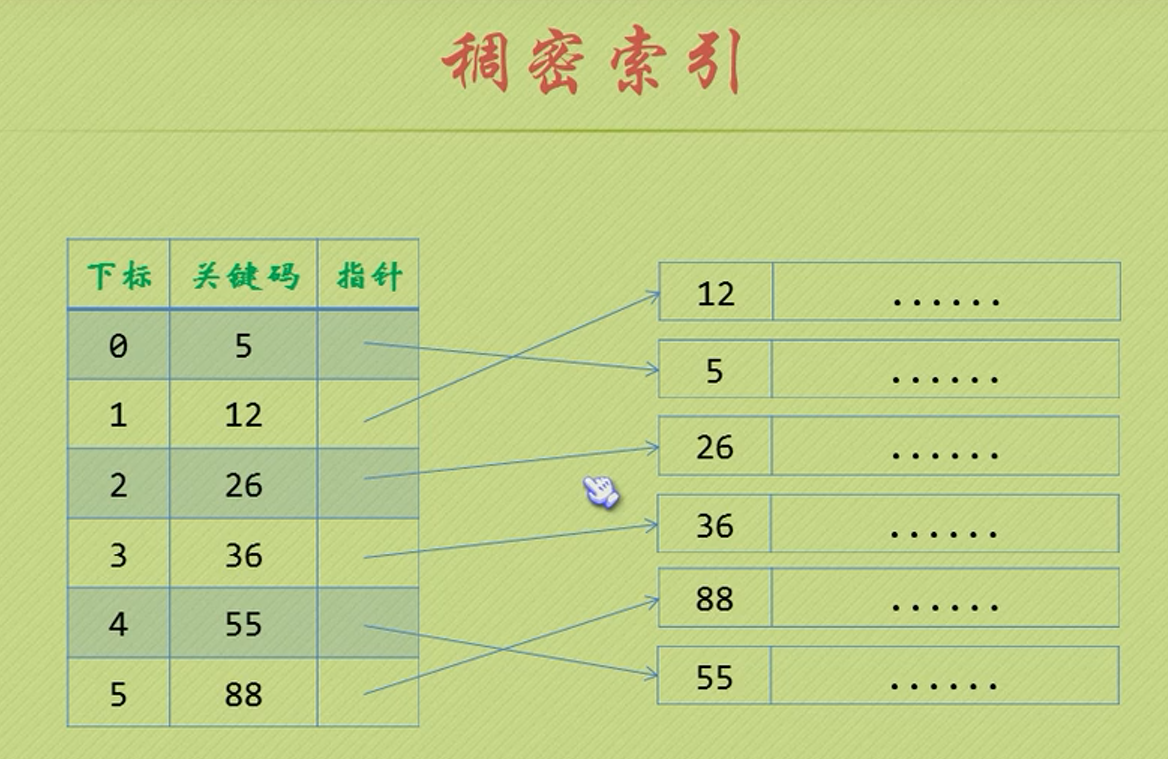
Dense index is used when the amount of data is not particularly large.

Block index
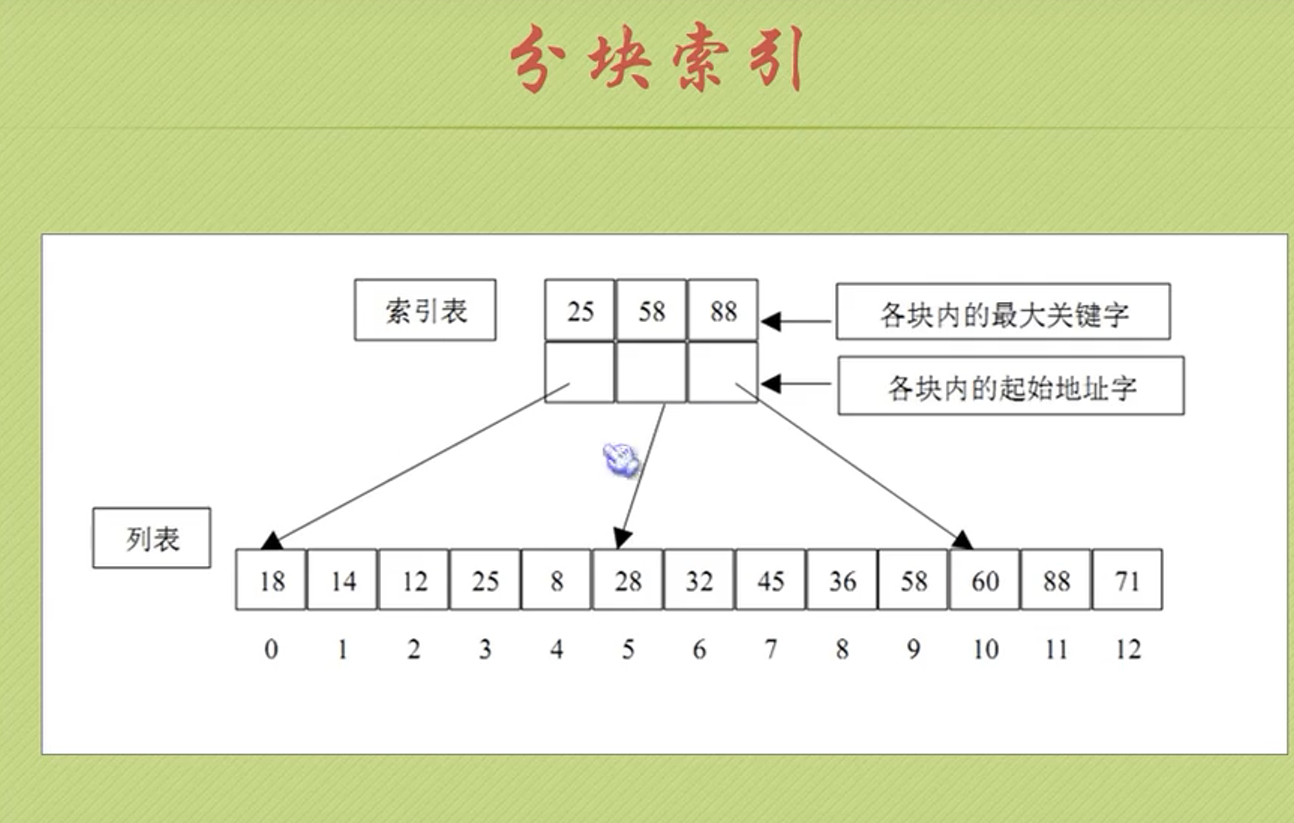


Inverted index



Binary sort tree

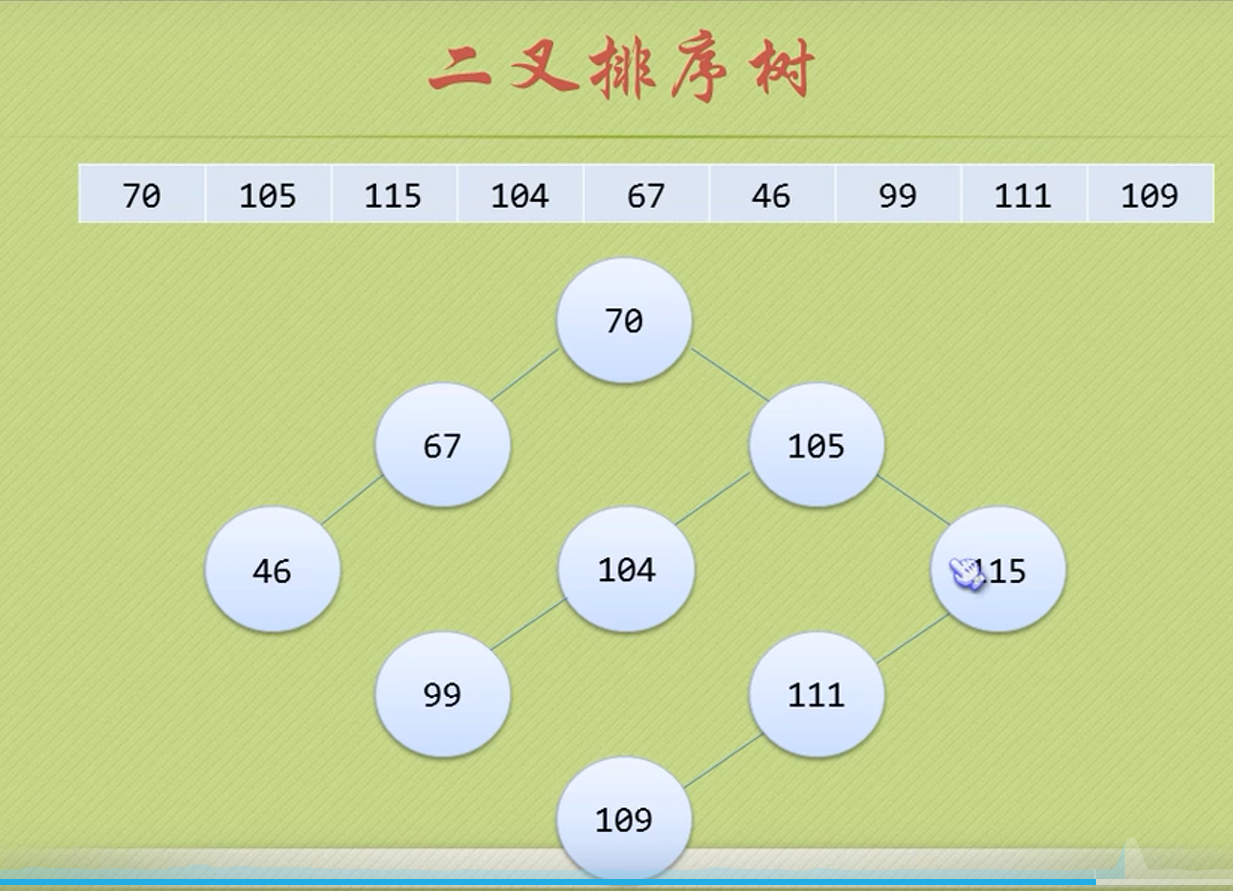
Binary sort tree is generated according to size
The general principle is that the big one is on the right and the small one is on the left

Binary sort tree lookup
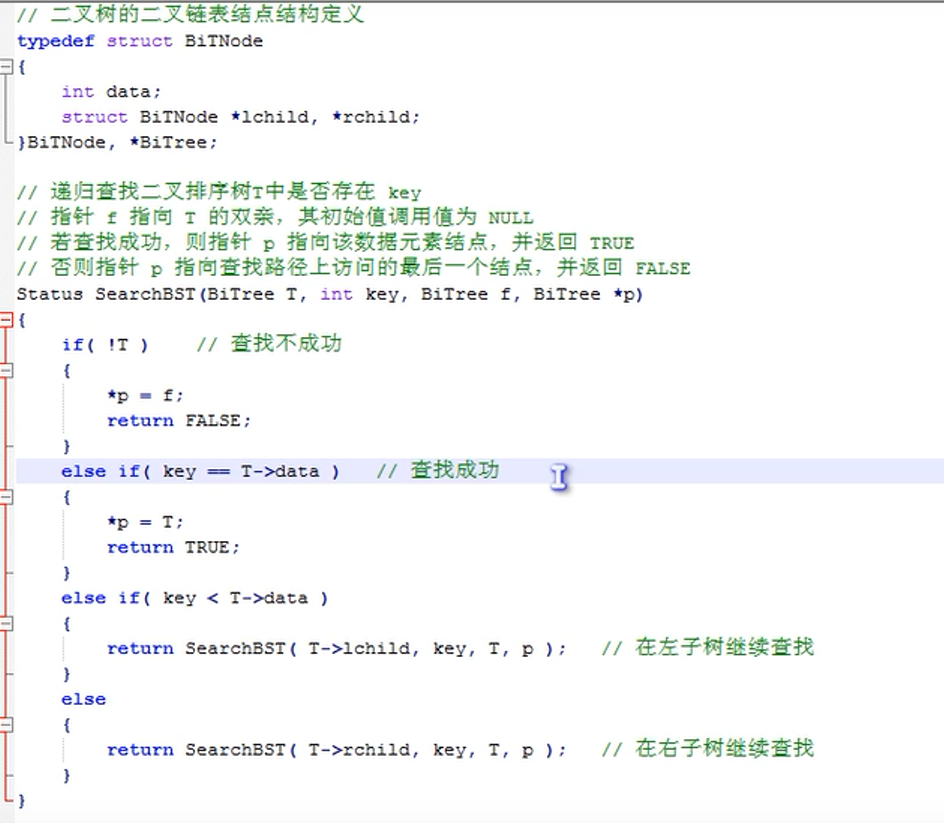
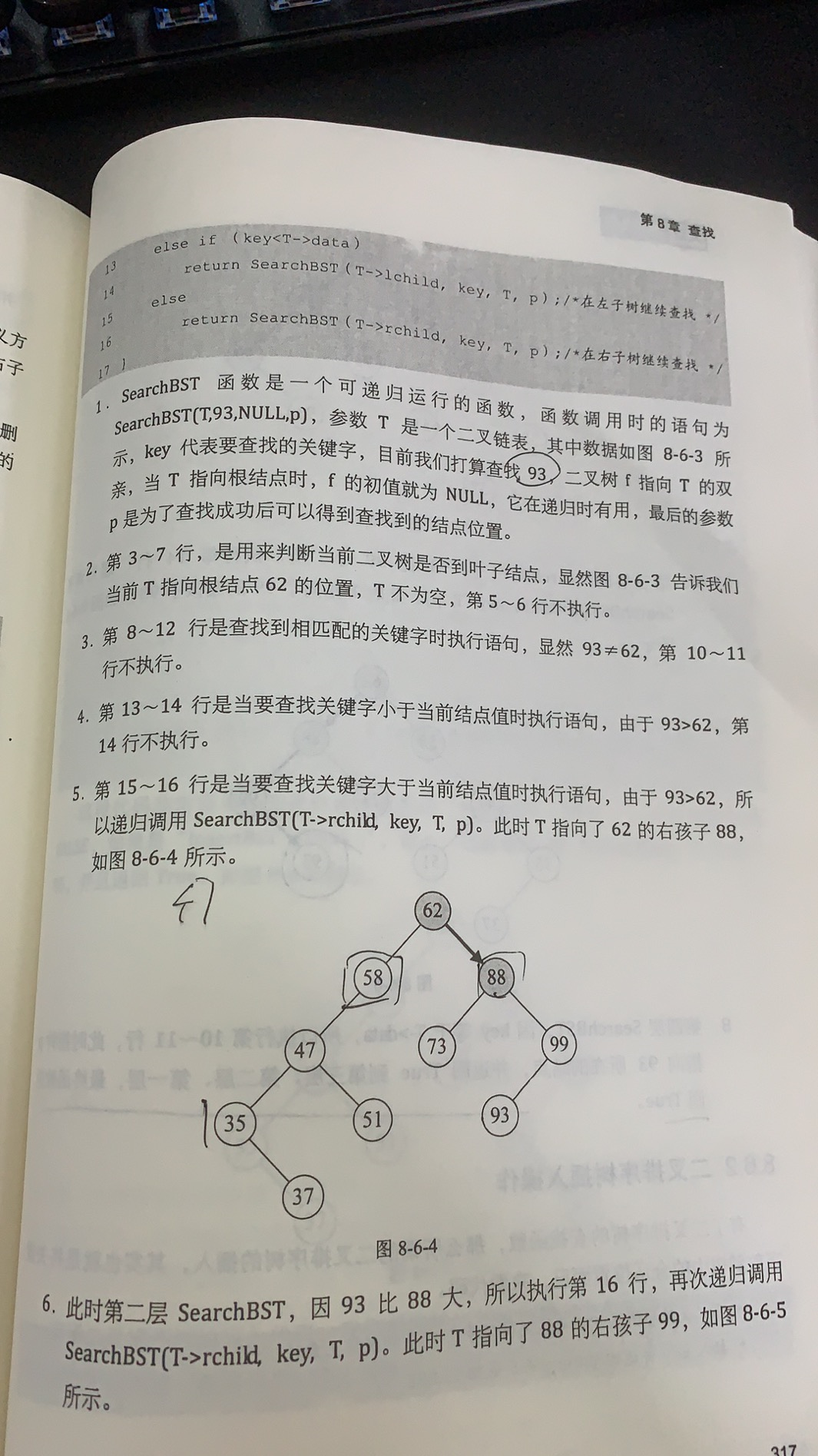
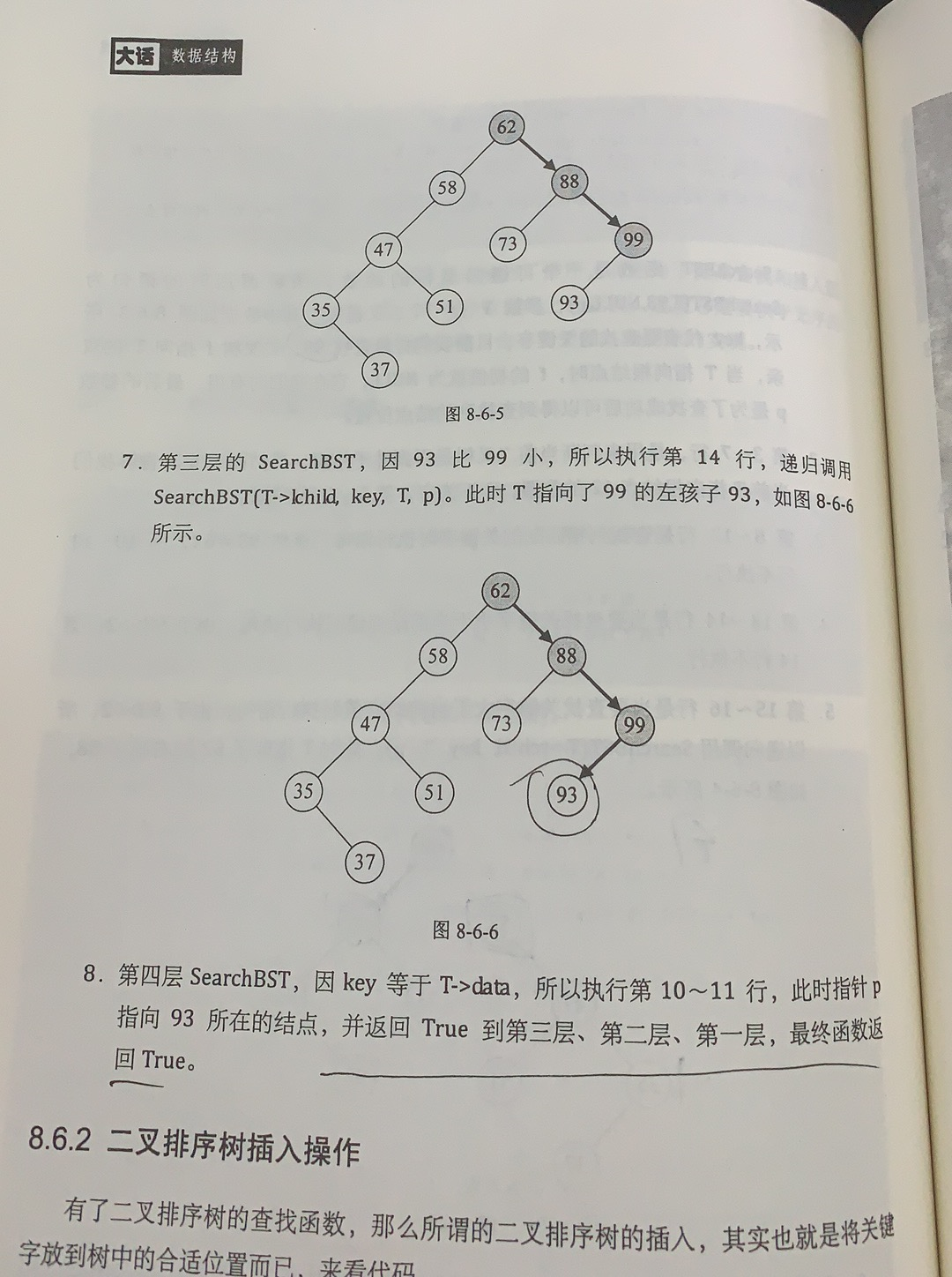
Binary sort tree insert

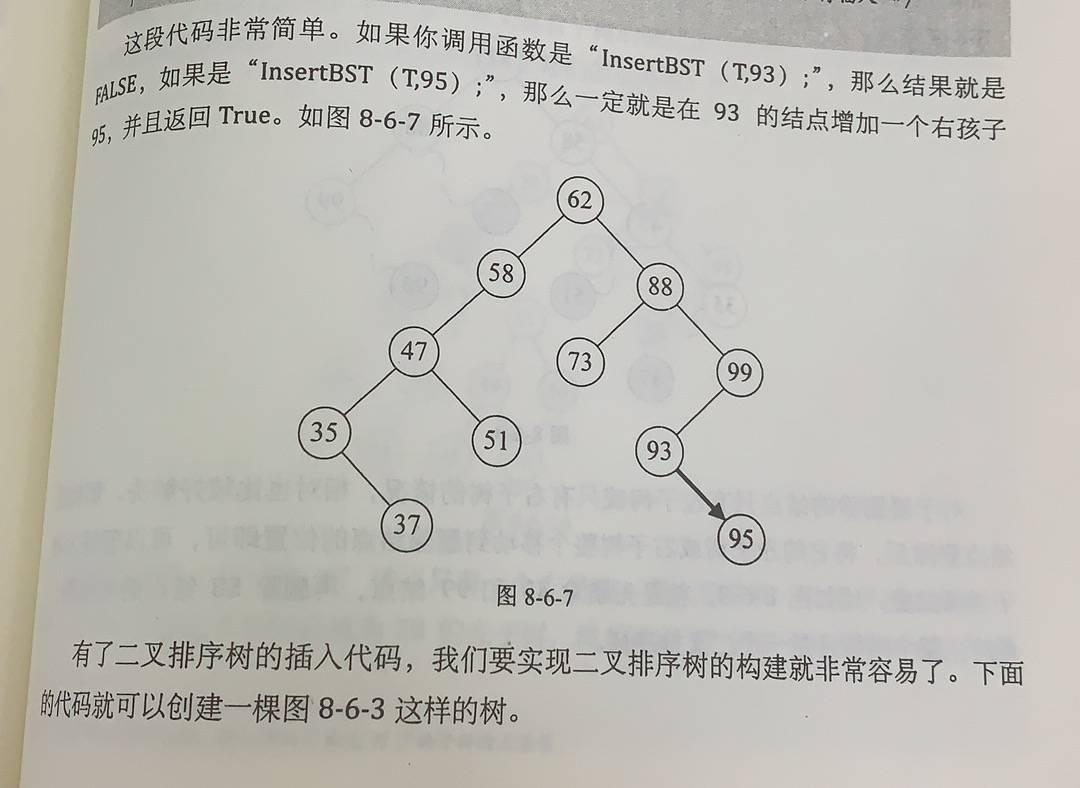

Binary sort tree delete
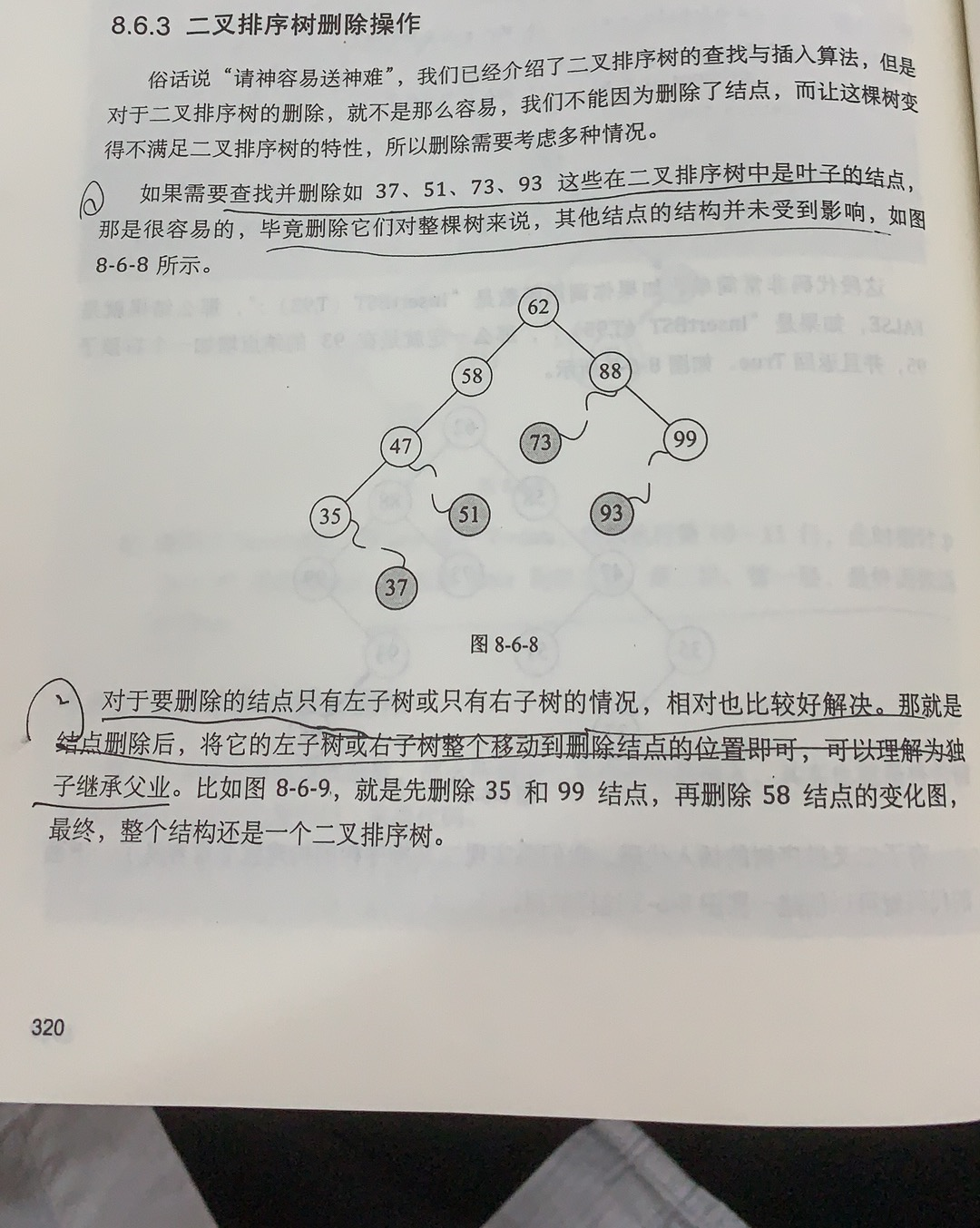
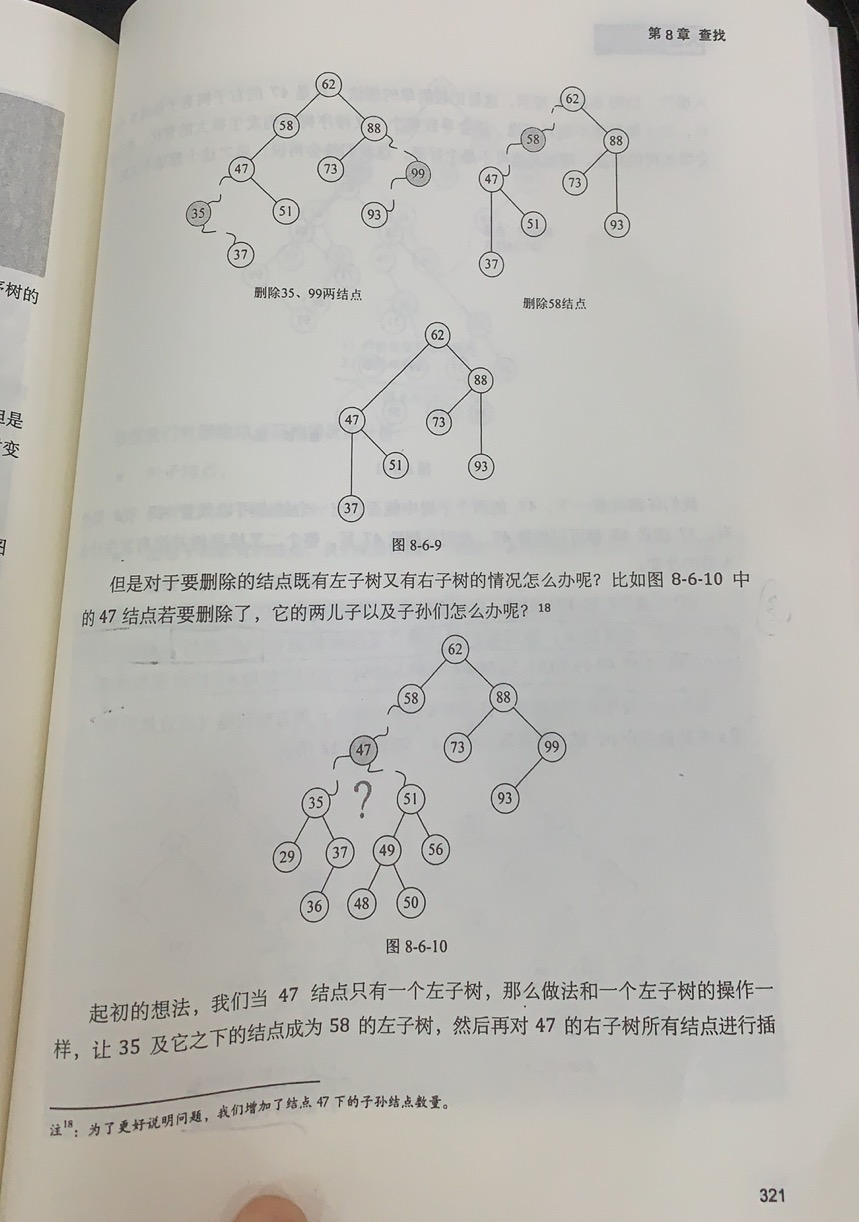
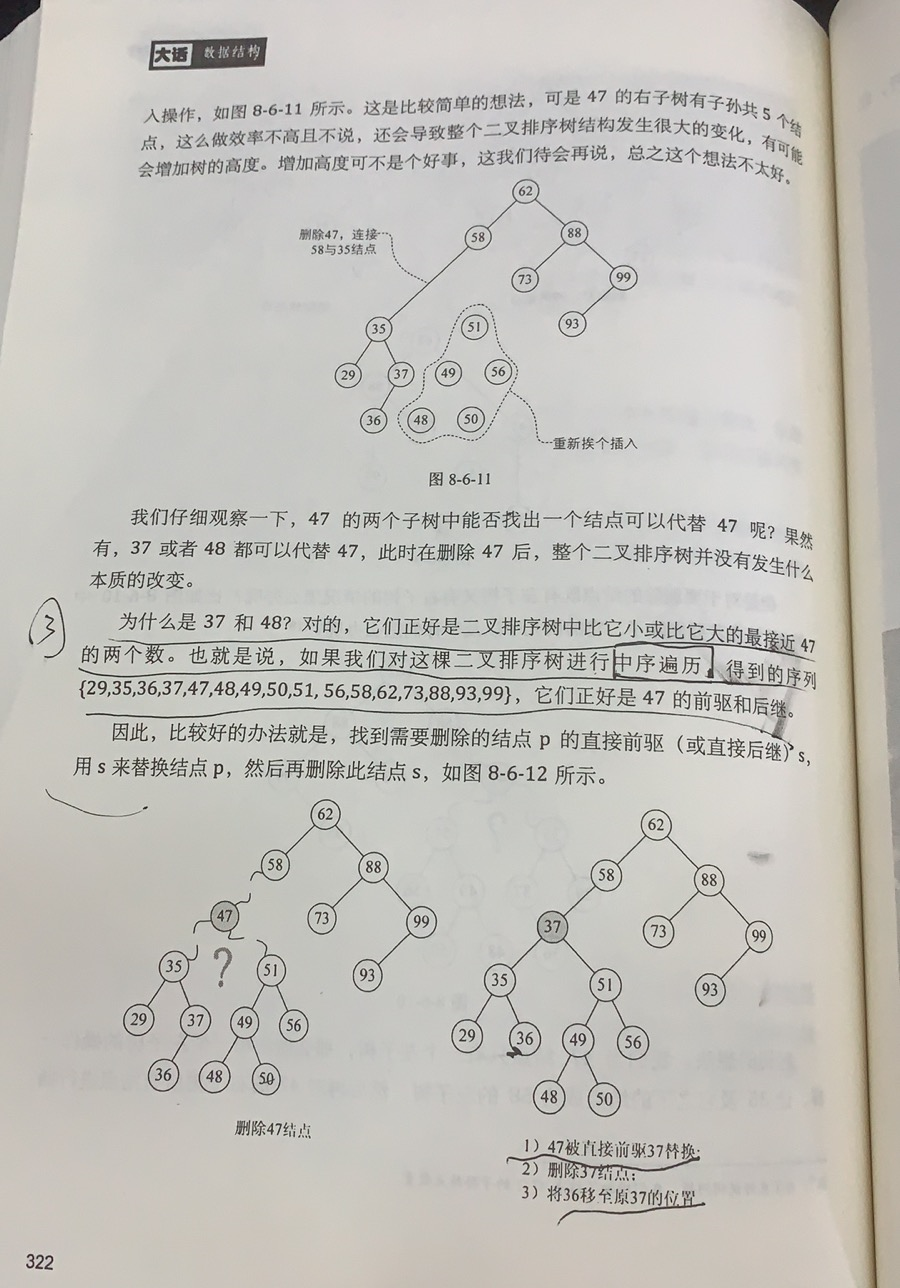
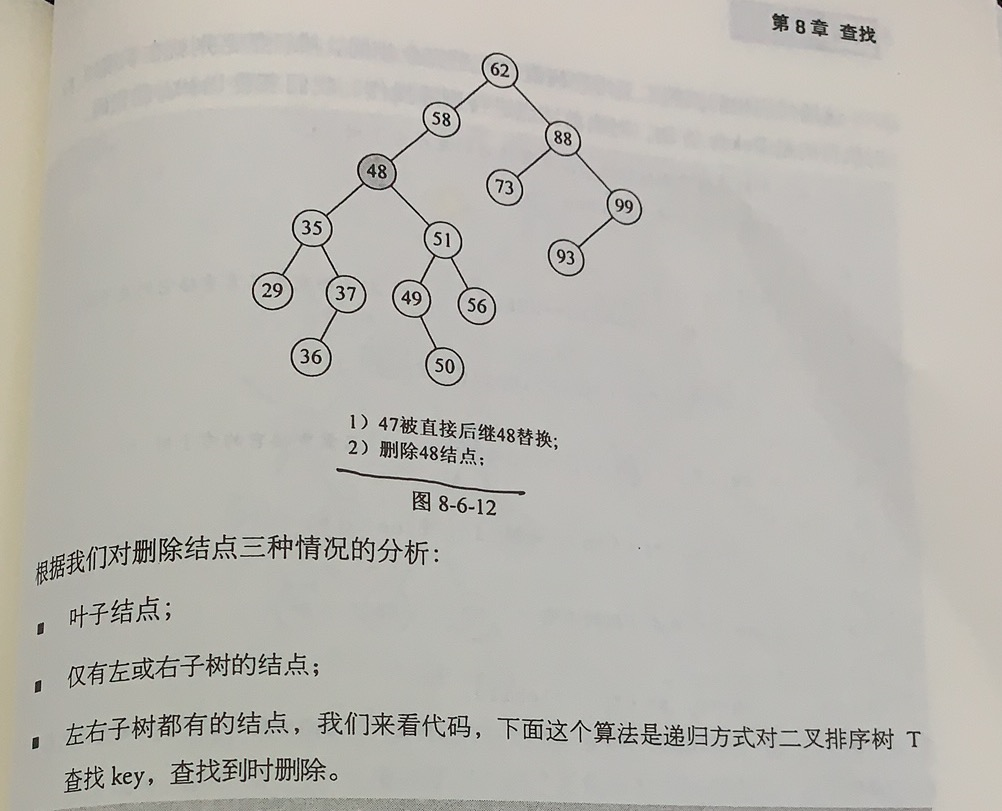
#include <iostream>
typedef struct BiTNode
{
int data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
typedef int Status;
#define TRUE 1
#define FALSE 0
//Binary tree sort lookup
Status SearchBST()
{
}
/**
* Specific deletion operation
* @param p
* @return
*/
Status Delete(BiTree *p)
{
BiTree q, s;
if((*p)->rchild==NULL)//The right subtree is empty
{
q=*p;
*p=(*p)->lchild;//Pick up the left sub tree
free(q);
}
else if((*p)->lchild==NULL)//Left subtree is empty
{
q=*p;
*p=(*p)->rchild;//Connect the right subtree
free(q);
}
//If the left and right subtrees are empty, just use the method that the top right subtree is empty
else//The left and right subtrees are not empty
{
//Replace with direct precursor
//How to find a direct precursor? Let s point directly to the left subtree of * p
//Then find the right subtree at the bottom of s, which is the precursor node
q=*p;
s=(*p)->lchild;
while(s->rchild)
{
q=s;
s=s->rchild;
}
(*p)->data=s->data;
if(q!=*p)//q here should be the precursor node of s
{
q->rchild=s->lchild;//Right subtree of reconnected q
}
else//That is, the left subtree of * p has no right subtree
{
q->lchild=s->lchild;//Reconnect the left subtree of Q, where q is actually (* p)
}
free(s);
}
return TRUE;
}
/**
* Binary tree sort delete operation
* @param T
* @param key
* @return
*/
Status DeleteBST(BiTree *T,int key)
{
if(!*T)
{
return FALSE;
}
else
{
if(key==(*T)->data)//Find the node to delete
{
return Delete(T);
}
else if(key<(*T)->data)//If the target value is less than the value of the current node, it is called recursively into the left subtree of the current node
{
return DeleteBST(&(*T)->lchild,key);
}
else //If the target value is greater than the value of the current node, it will be called recursively to enter the right subtree of the current node
{
return DeleteBST(&(*T)->rchild,key);
}
}
}
balanced binary tree


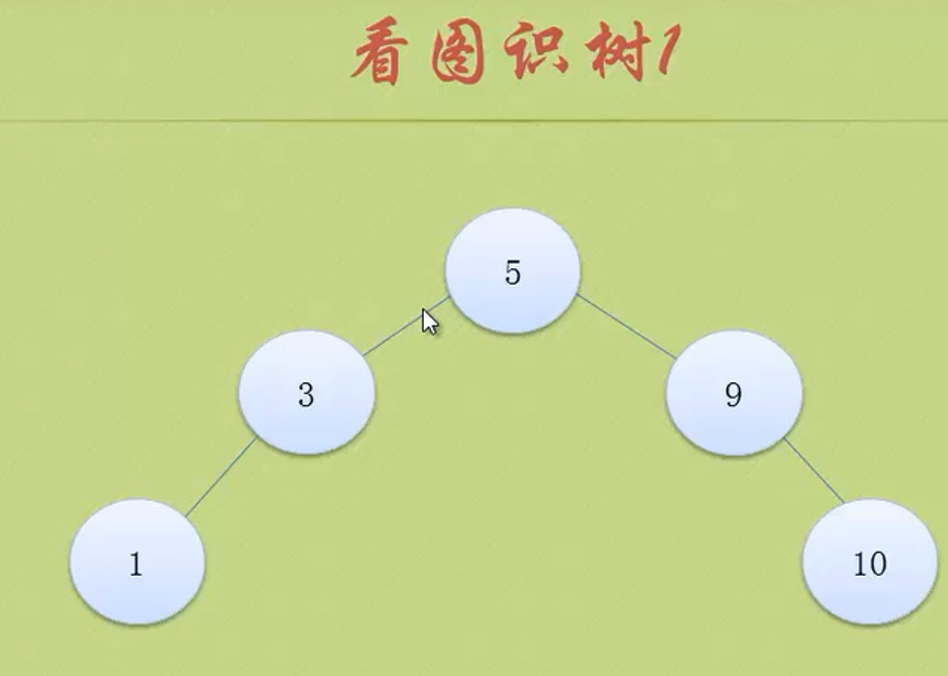
The figure above is a balanced binary sort tree
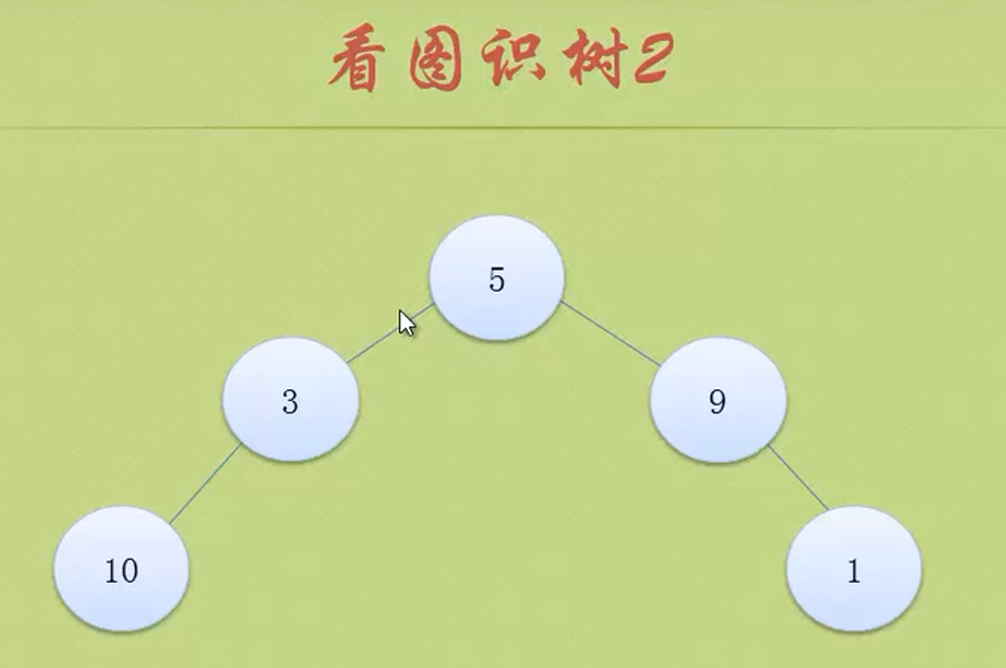
The above figure is not a balanced binary sort tree. It is not even a binary sort tree
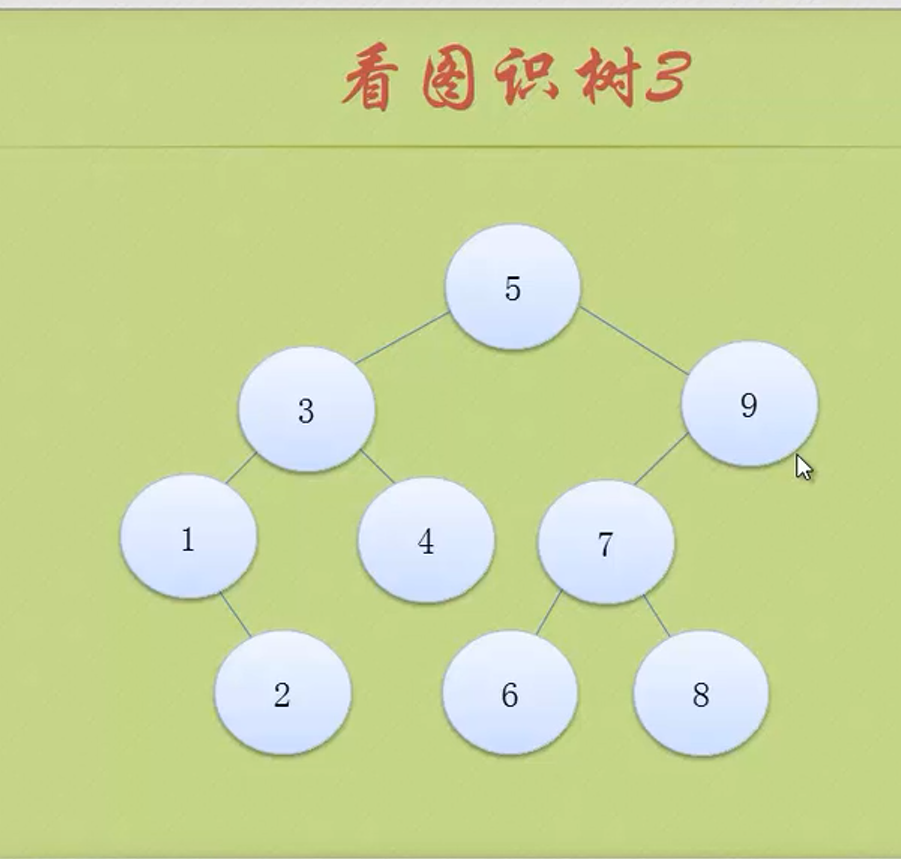
The above figure is not a balanced binary sort tree either, because for 9 node, the left subtree depth is 2, the right subtree depth is 0, and 2-0 = 2 does not meet the condition of balanced binary tree
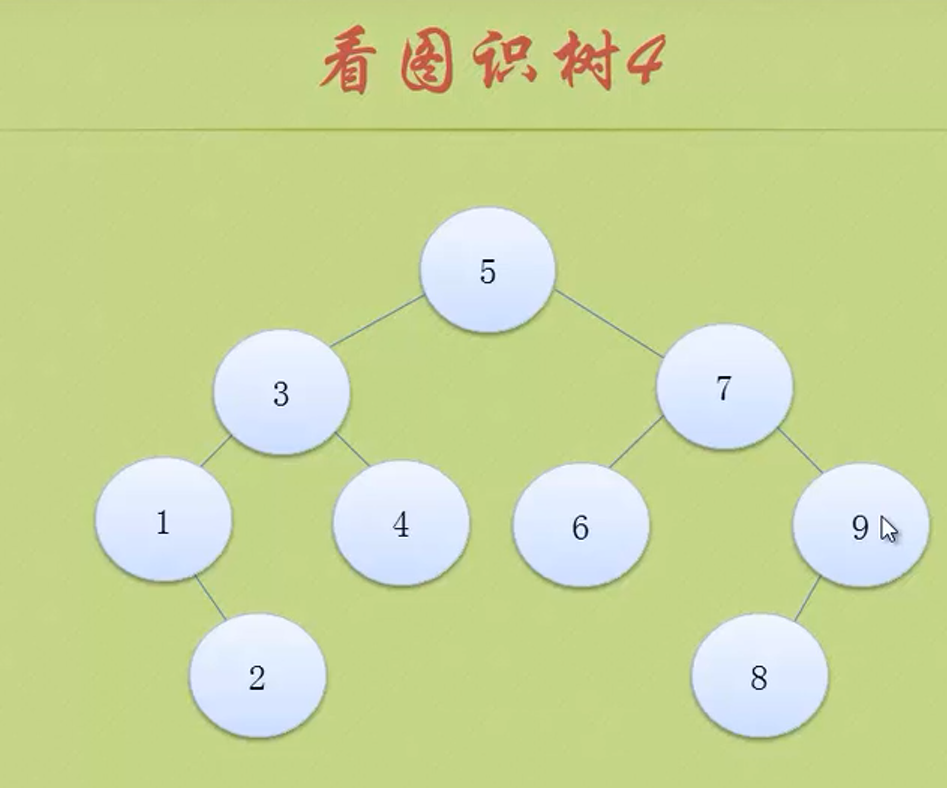
The above figure is a balanced binary sort tree
How to convert Figure 3 into the balanced binary sort tree in Figure 4.
Whenever this node is inserted, check whether this node will cause imbalance, that is, whether the balance factor is greater than 1.
For example, when node 6 is inserted, the balance factor of node 9 is > 1.
9, 7 and 6 constitute the smallest tree.
Let's ignore 8 this node first
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-lxgduas7-1632886438959) (C: \ users \ Dell \ appdata \ roaming \ typora \ user images \ image-20210923150821420. PNG)]
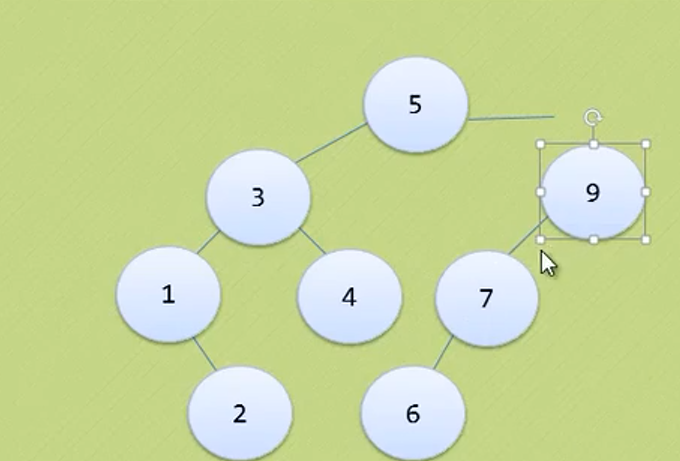
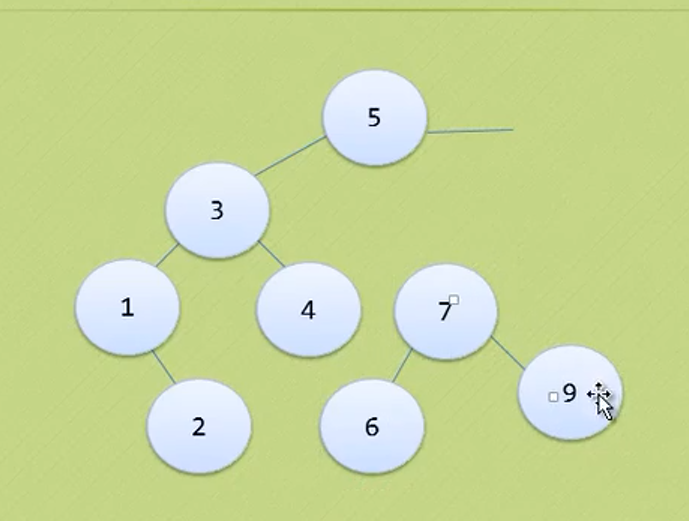
principle
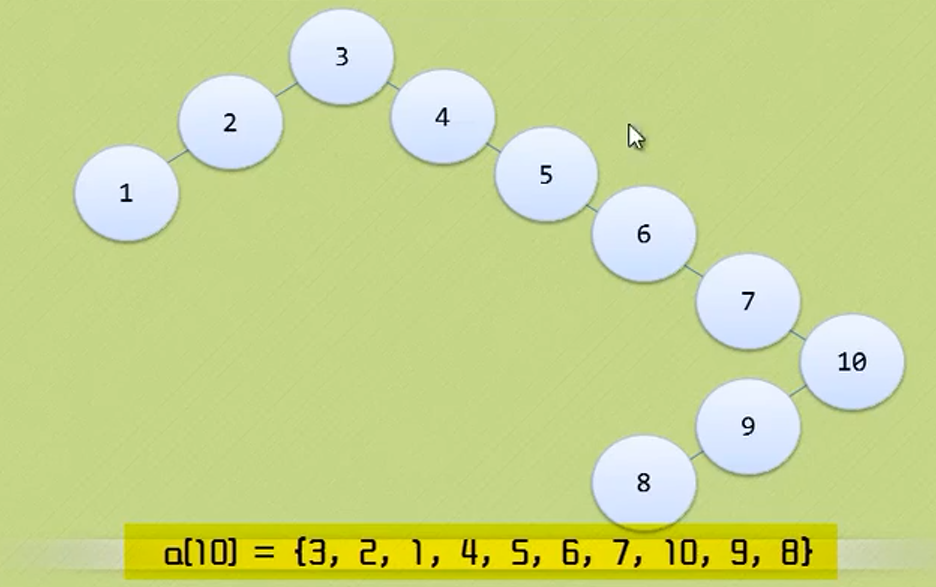
The figure above is an ordinary binary sort tree
How to turn the ordinary binary sort tree in the figure above into a balanced binary sort tree? Let's do it step by step!!!
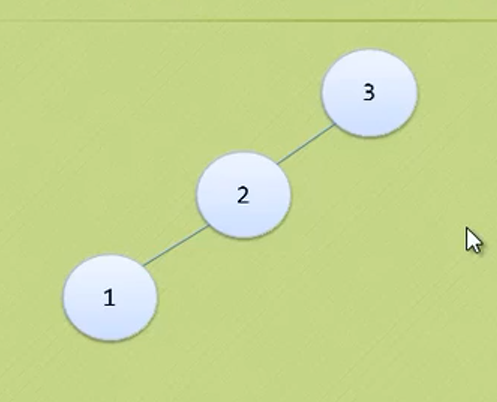
BF > 1 right rotation
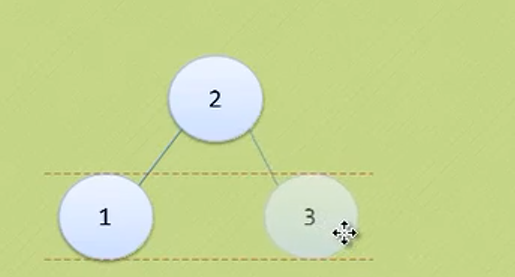
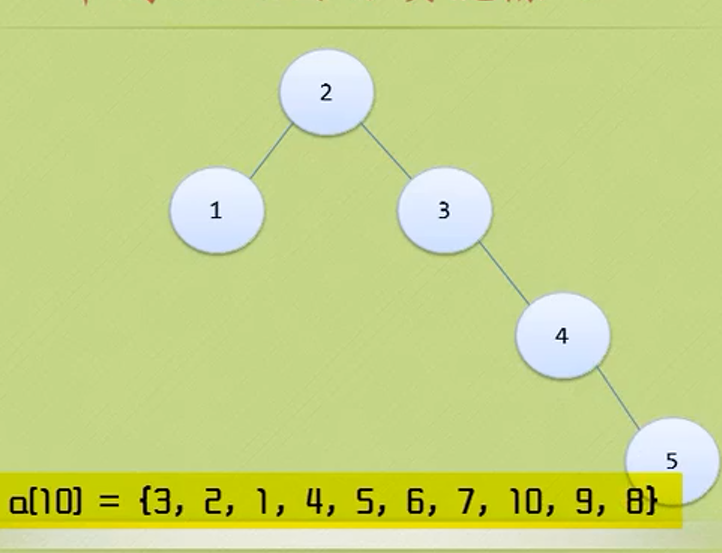
BF < - 1 left rotation
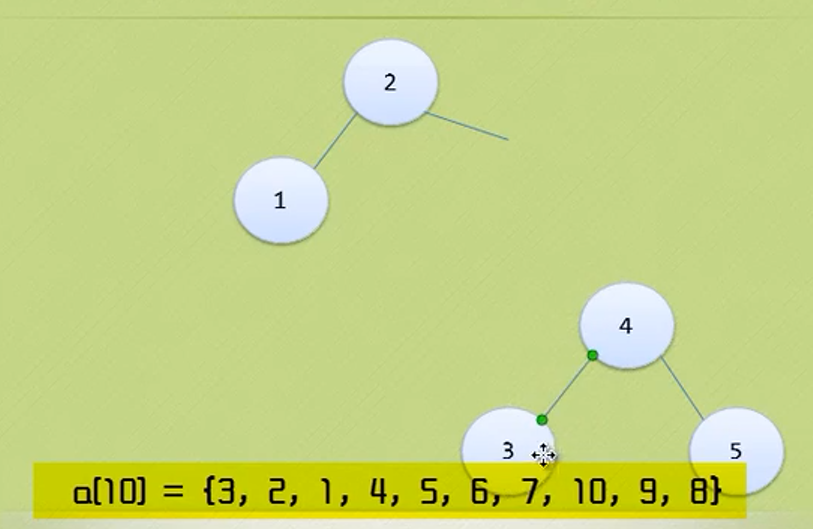
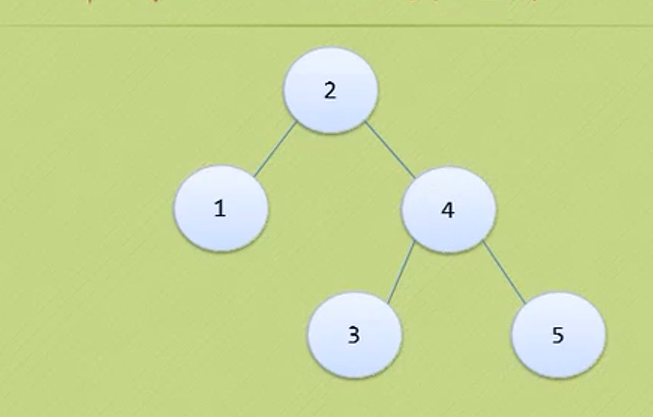
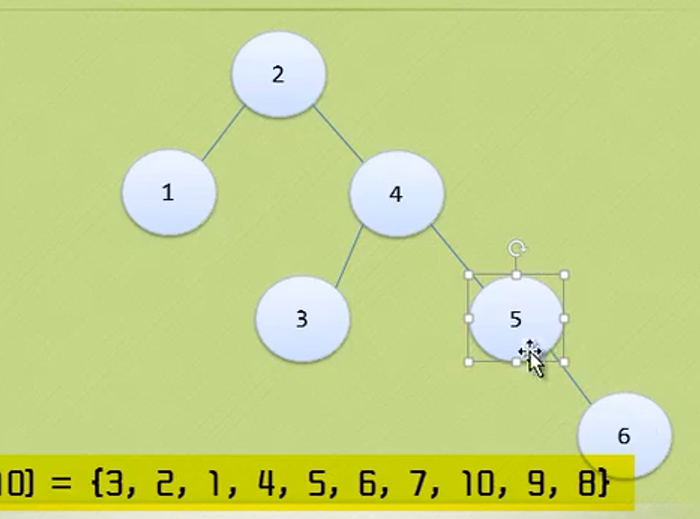
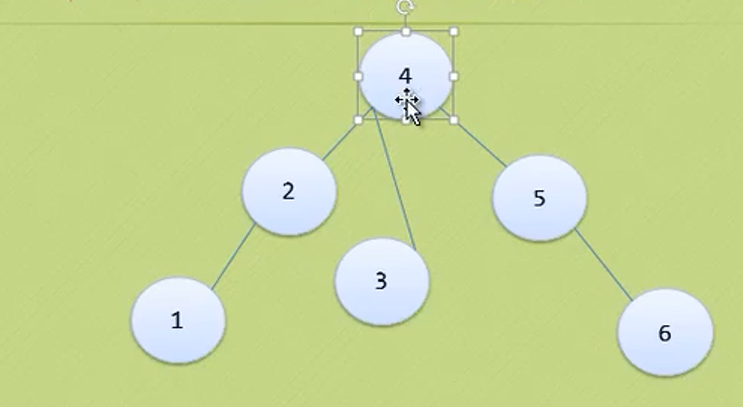
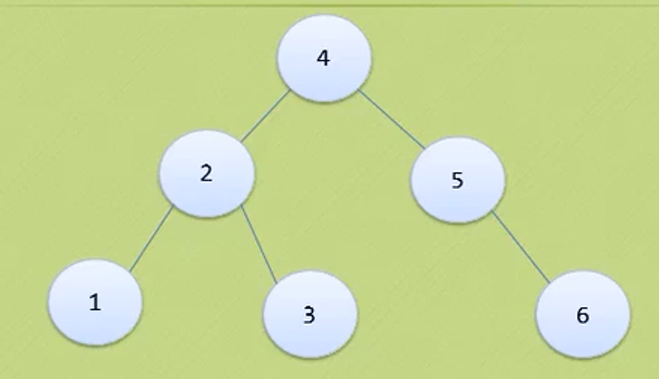
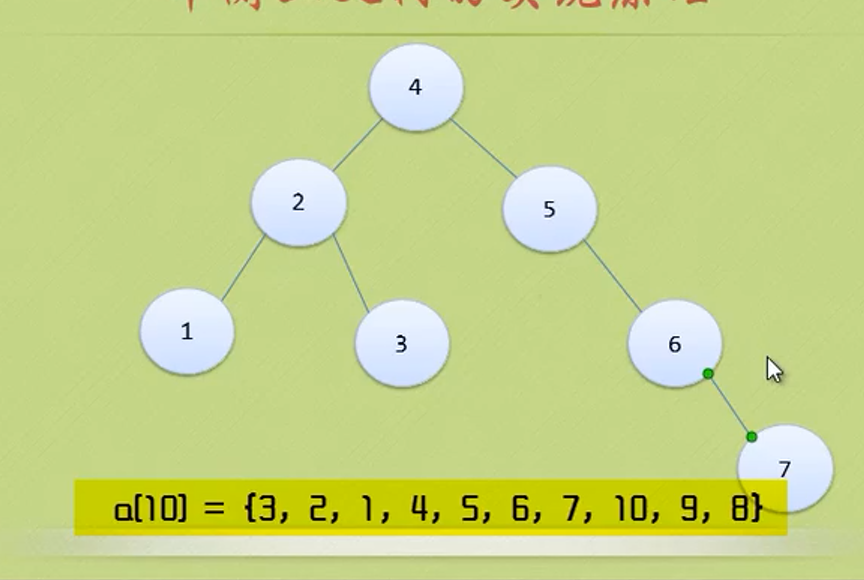
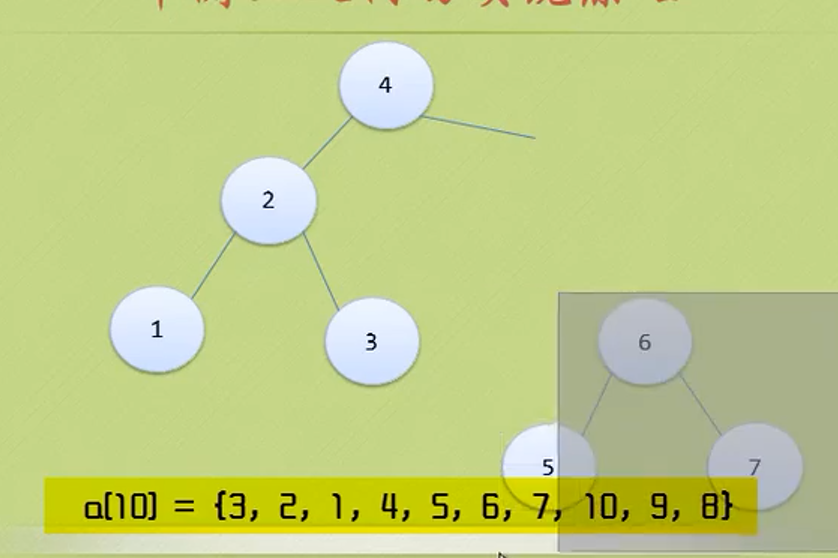
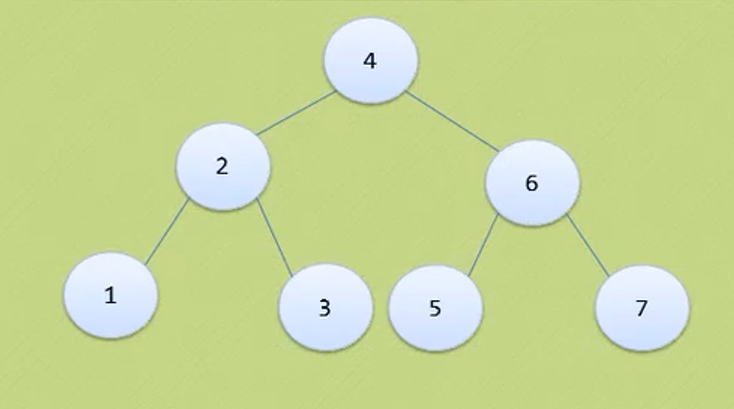
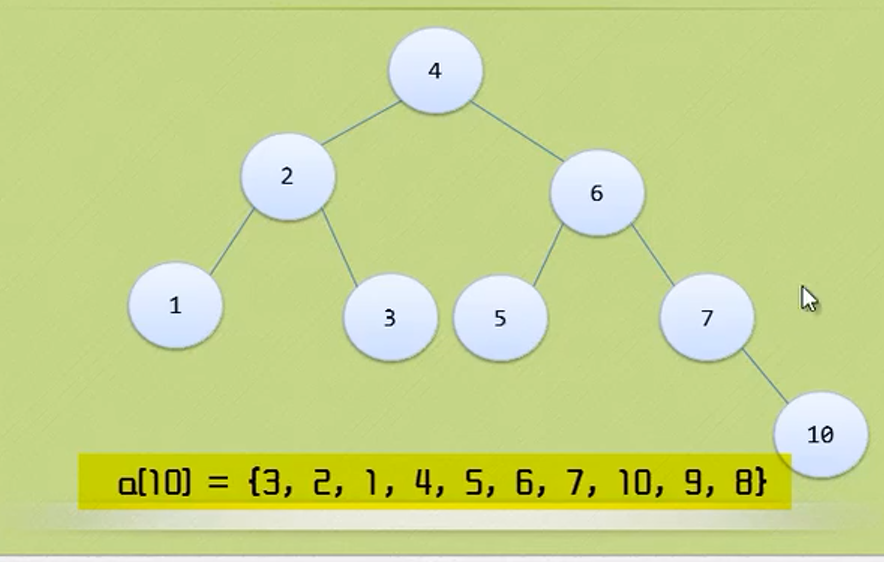
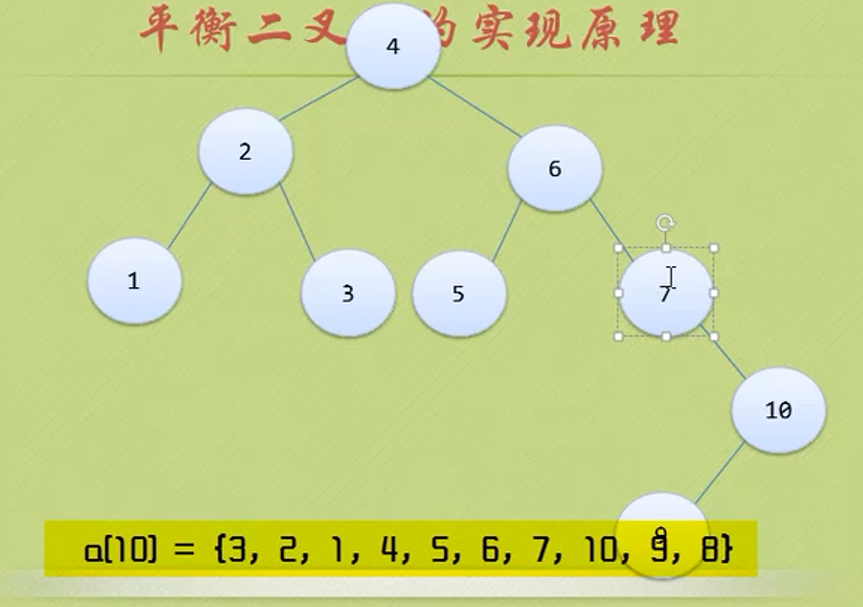
When node 9 comes in, it leads to node 4 BF=-2, node 6 BF=-2, node 7 BF=-2 and node 10 BF=1. It is strange that only the BF of node 10 is positive
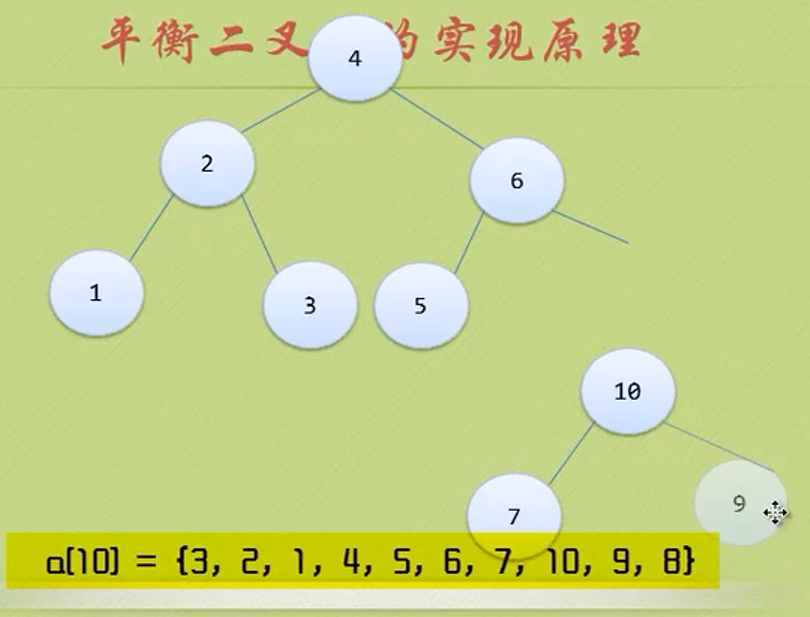
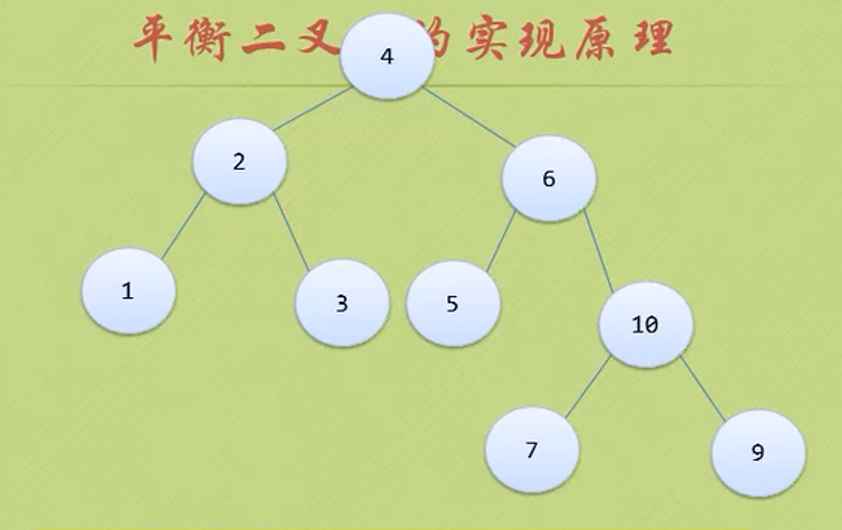
This is obviously not in line with the rules of binary tree sorting.
So we should deal with 9 and 10 first

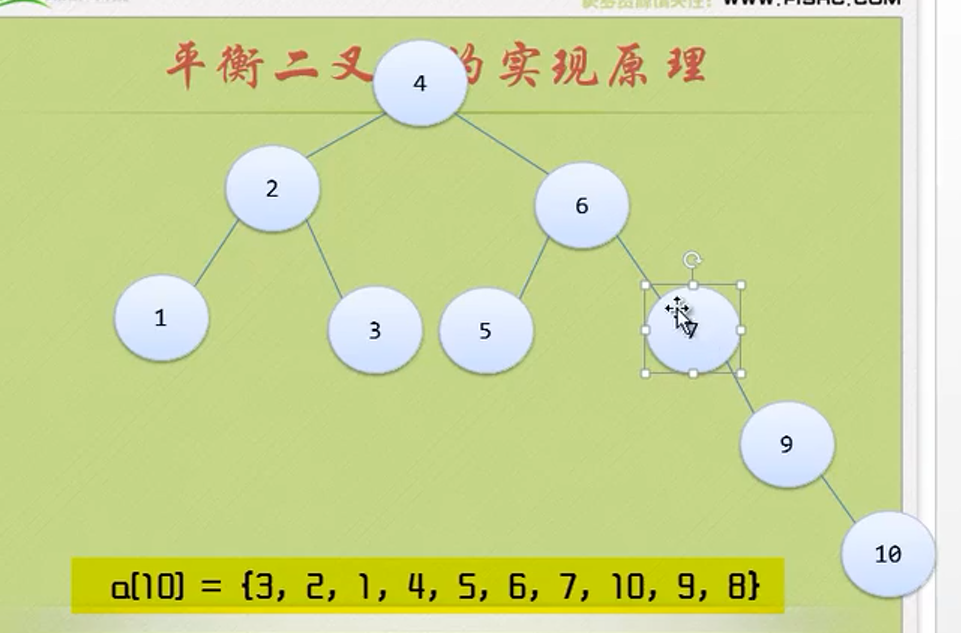
Let the BF of nodes 4, 6, 7, 9 and 10 be negative
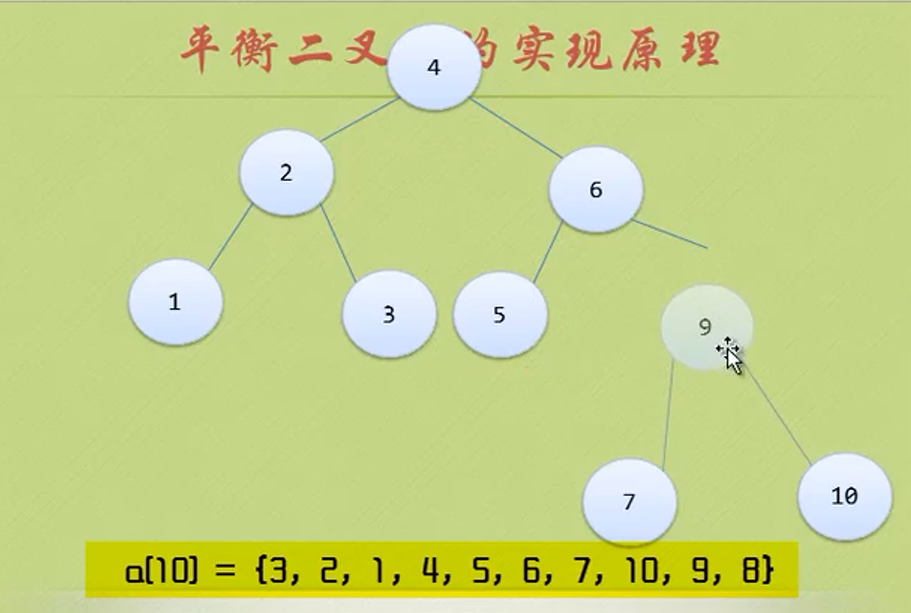
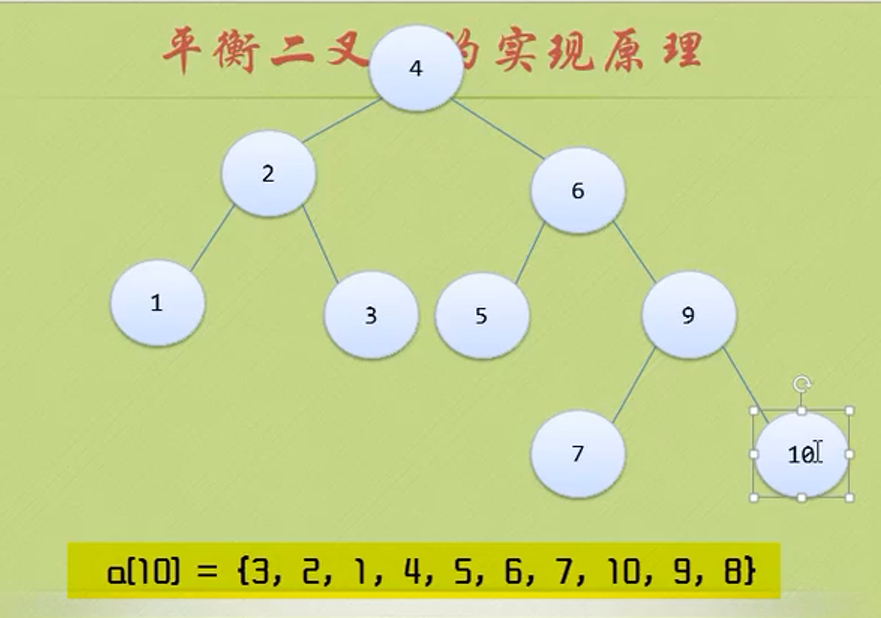
Join node 8
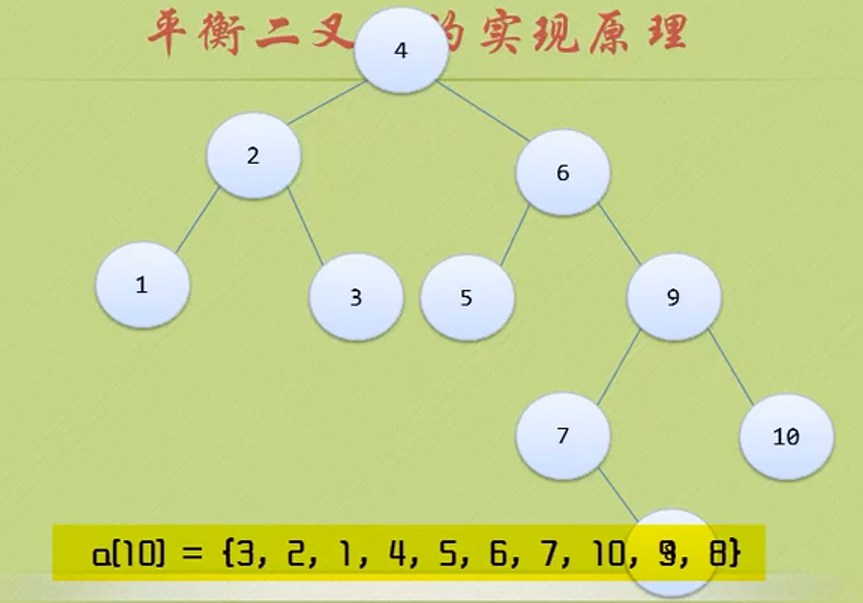
The BF of node 4 and node 6 is - 2, and the BF of node 9 is 1, which is a positive number
So we should first deal with node 7 8 9 10 so that the BF of node 7 9 10 is also negative
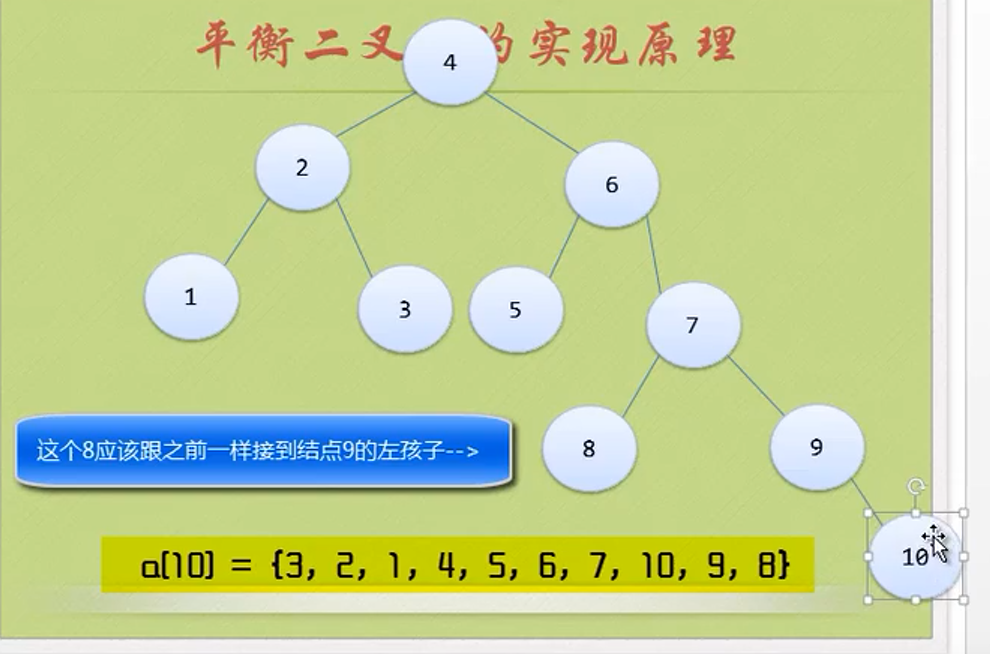
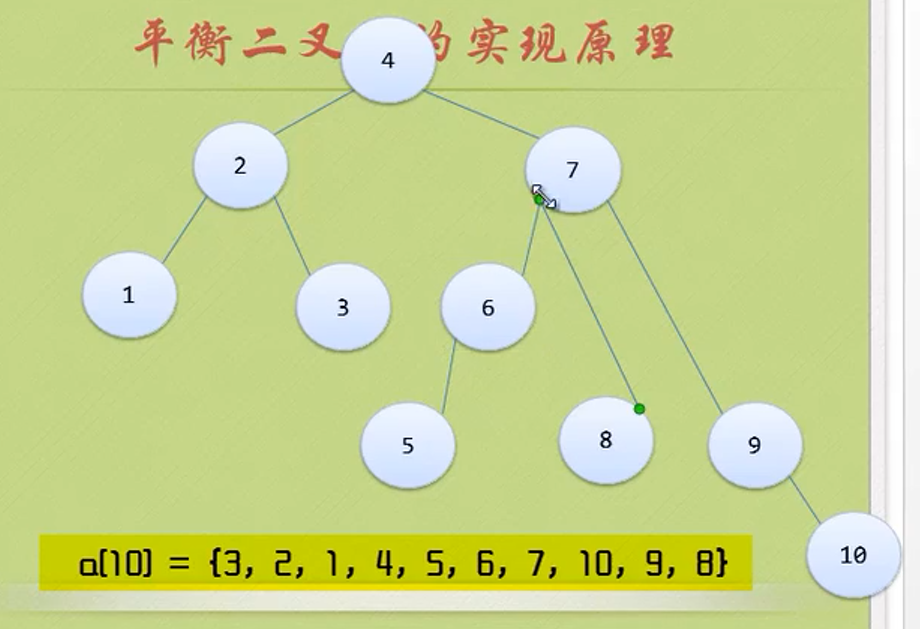
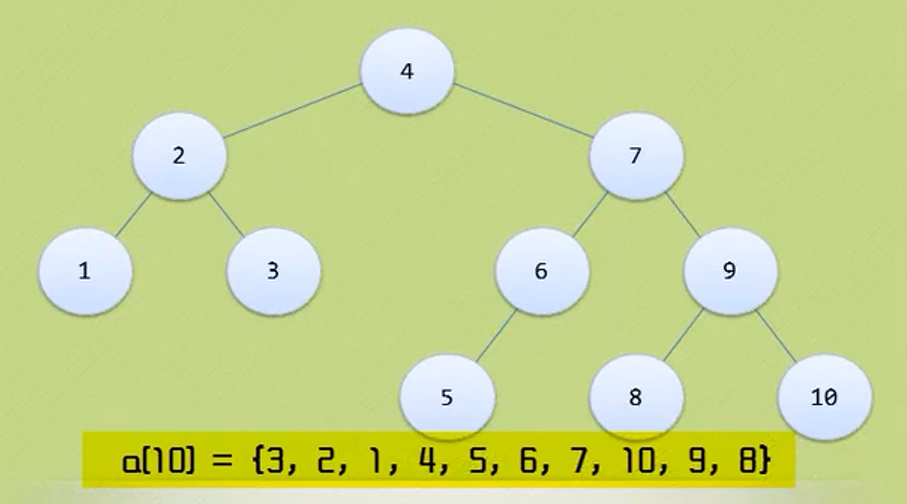
realization
#include <iostream>
typedef struct BiTNode
{
int data;
int bf;//Equilibrium factor
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
typedef int Status;
#define TRUE 1
#define FALSE 0
#define LH 1 / / the left subtree is too high
#define EH 0 / / left and right subtrees are equal in height
#define RH -1 / / the right subtree is too high
/**
* Right rotation
* @param p
*/
void R_Rotate(BiTree *p)
{
BiTree L;
L=(*p)->lchild;
(*p)->lchild=L->rchild;
L->rchild=(*p);
*p=L;//Point to the new root node
}
/**
* Left rotation
* @param p
*/
void L_Rotate(BiTree *p)
{
BiTree R;
R=(*p)->rchild;
(*p)->rchild=R->lchild;
R->lchild=(*p);
*p=R;//Point to the new root node
}
/**
* Left balance
* @param T
*/
void LeftBalance(BiTree *T)
{
BiTree L,Lr;
L=(*T)->lchild;
switch (L->bf)//T's left child's bf
{
case LH://This indicates that L is the same sign as BF of the root node, and the root node can be rotated right, and the balance is restored after rotation, so the value of BF should also be modified
(*T)->bf=L->bf=EH;
R_Rotate(T);
break;
case RH://This indicates that L is opposite to the BF symbol of the root node. Rotate L left and then rotate the root node right
Lr=L->rchild;
//It's the switch below. I can't figure it out!!!!
switch (Lr->bf)
{
case LH://
(*T)->bf=RH;
L->bf=EH;
break;
case EH://
(*T)->bf=L->bf=EH;
break;
case RH://
(*T)->bf=EH;
L->bf=LH;
break;
}
Lr->bf=EH;
L_Rotate(&(*T)->lchild);//Make symbols the same
R_Rotate(T);
break;
}
}
/**
* Right balance
* @param T
*/
void RightBalance(BiTree *T)
{
BiTree R,Rl;
R=(*T)->rchild;
switch (R->bf)//T's left child's bf
{
case RH://This indicates that R is the same sign as BF of the root node, and the root node can be rotated to the left, and the balance is restored after rotation, so the value of BF should also be modified
(*T)->bf=R->bf=EH;
L_Rotate(T);
break;
case LH://This indicates that R is opposite to the BF symbol of the root node. Rotate r right and then rotate the root node left
Rl=R->lchild;
//It's the switch below. I can't figure it out!!!!
switch (Rl->bf)
{
case RH://You can also draw a picture and assume
(*T)->bf=LH;
R->bf=EH;
break;
case EH://
(*T)->bf=R->bf=EH;
break;
case LH:// Here you can draw your own picture and suppose
(*T)->bf=EH;
R->bf=RH;
break;
}
Rl->bf=EH;
R_Rotate(&(*T)->rchild);//Make symbols the same
L_Rotate(T);
break;
}
}
/**
*
* @param T
* @param e Inserted data
* @param taller If the tree grows tall, it will be unbalanced
* @return
*/
int InsertAVL(BiTree *T,int e,int *taller)
{
if(!*T)
{
*T=(BiTree)malloc(sizeof(BiTNode));
(*T)->data=e;
(*T)->lchild=(*T)->rchild=NULL;
(*T)->bf=EH;
*taller=TRUE;
}
//Detect each node in real time
else
{
if(e==(*T)->data)//There is already a value to insert
{
*taller=FALSE;
}
if(e<(*T)->data)//Go left and insert left subtree
{
if(!InsertAVL(&(*T)->lchild,e,taller))//recursion
{
return FALSE;//If you find the same, return FALSE
}
if(*taller)//We'll test it when we grow tall
{
switch ((*T)->bf)
{
case LH://The left subtree is higher than the right subtree, so we have to deal with it
LeftBalance(T);//handle
*taller=FALSE;
break;
case EH://It was originally a balance between the left and right subtrees. Now we need to add a left subtree, so the left subtree is higher than the right subtree
(*T)->bf=LH;
*taller=TRUE;
break;
case RH://Originally, the right subtree is higher than the left subtree, and then add a left subtree to balance it
(*T)->bf=EH;
*taller=FALSE;
break;
}
}
}
else//Go right and insert right subtree
{
if(!InsertAVL(&(*T)->rchild,e,taller))//recursion
{
return FALSE;//If you find the same, return FALSE
}
if(*taller)//We'll test it when we grow tall
{
switch ((*T)->bf)
{
case LH://Originally, the left subtree is higher than the right subtree, and then add a right subtree to balance it
(*T)->bf=EH;
*taller=FALSE;
break;
case EH://It was originally a balance between the left and right subtrees. Now we need to add a right subtree, so the right subtree is higher than the left subtree
(*T)->bf=RH;
*taller=TRUE;
break;
case RH://Originally, the right subtree is higher than the left subtree, and then a right subtree is added, which needs to deal with balance
RightBalance(T);//handle
*taller=FALSE;
break;
}
}
}
}
return TRUE;
}
int main() {
int i;
int a[10]={3,2,1,4,5,6,7,10,9,8};
BiTree T=NULL;
Status taller;
for(i=0;i<10;i++)
{
InsertAVL(&T,a[i],&taller);
}
return 0;
}
summary
Several corresponding cases in the right balance function
/**
* Right balance
* @param T
*/
void RightBalance(BiTree *T)
{
BiTree R,Rl;
R=(*T)->rchild;
switch (R->bf)//T's left child's bf
{
case RH://This indicates that R is the same sign as BF of the root node, and the root node can be rotated to the left, and the balance is restored after rotation, so the value of BF should also be modified
(*T)->bf=R->bf=EH;
L_Rotate(T);
break;
case LH://This indicates that R is opposite to the BF symbol of the root node. Rotate r right and then rotate the root node left
Rl=R->lchild;
//It's the switch below. I can't figure it out!!!!
switch (Rl->bf)
{
case RH://
(*T)->bf=LH;
R->bf=EH;
break;
case EH://I can't find a specific example of this situation
(*T)->bf=R->bf=EH;
break;
case LH://I always feel that there is something wrong. Here I can draw my own picture. Suppose I think there is something wrong
(*T)->bf=EH;
R->bf=RH;
break;
}
Rl->bf=EH;
R_Rotate(&(*T)->rchild);//Make symbols the same
L_Rotate(T);
break;
}
}
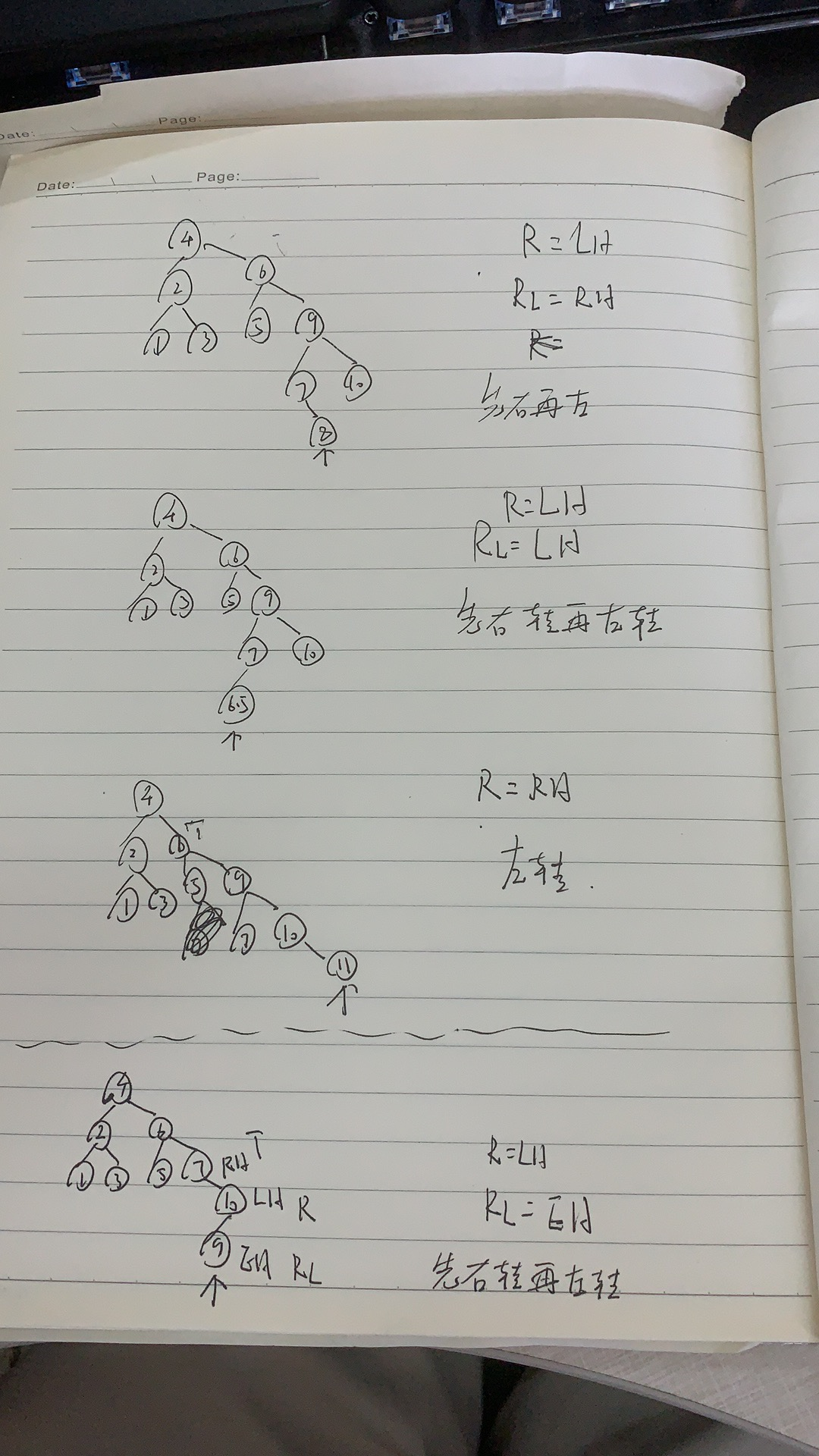
Several cases in left equilibrium function
/**
* Left balance
* @param T
*/
void LeftBalance(BiTree *T)
{
BiTree L,Lr;
L=(*T)->lchild;
switch (L->bf)//T's left child's bf
{
case LH://This indicates that L is the same sign as BF of the root node, and the root node can be rotated right, and the balance is restored after rotation, so the value of BF should also be modified
(*T)->bf=L->bf=EH;
R_Rotate(T);
break;
case RH://This indicates that L is opposite to the BF symbol of the root node. Rotate L left and then rotate the root node right
Lr=L->rchild;
//It's the switch below. I can't figure it out!!!!
switch (Lr->bf)
{
case LH://
(*T)->bf=RH;
L->bf=EH;
break;
case EH://
(*T)->bf=L->bf=EH;
break;
case RH://
(*T)->bf=EH;
L->bf=LH;
break;
}
Lr->bf=EH;
L_Rotate(&(*T)->lchild);//Make symbols the same
R_Rotate(T);
break;
}
}
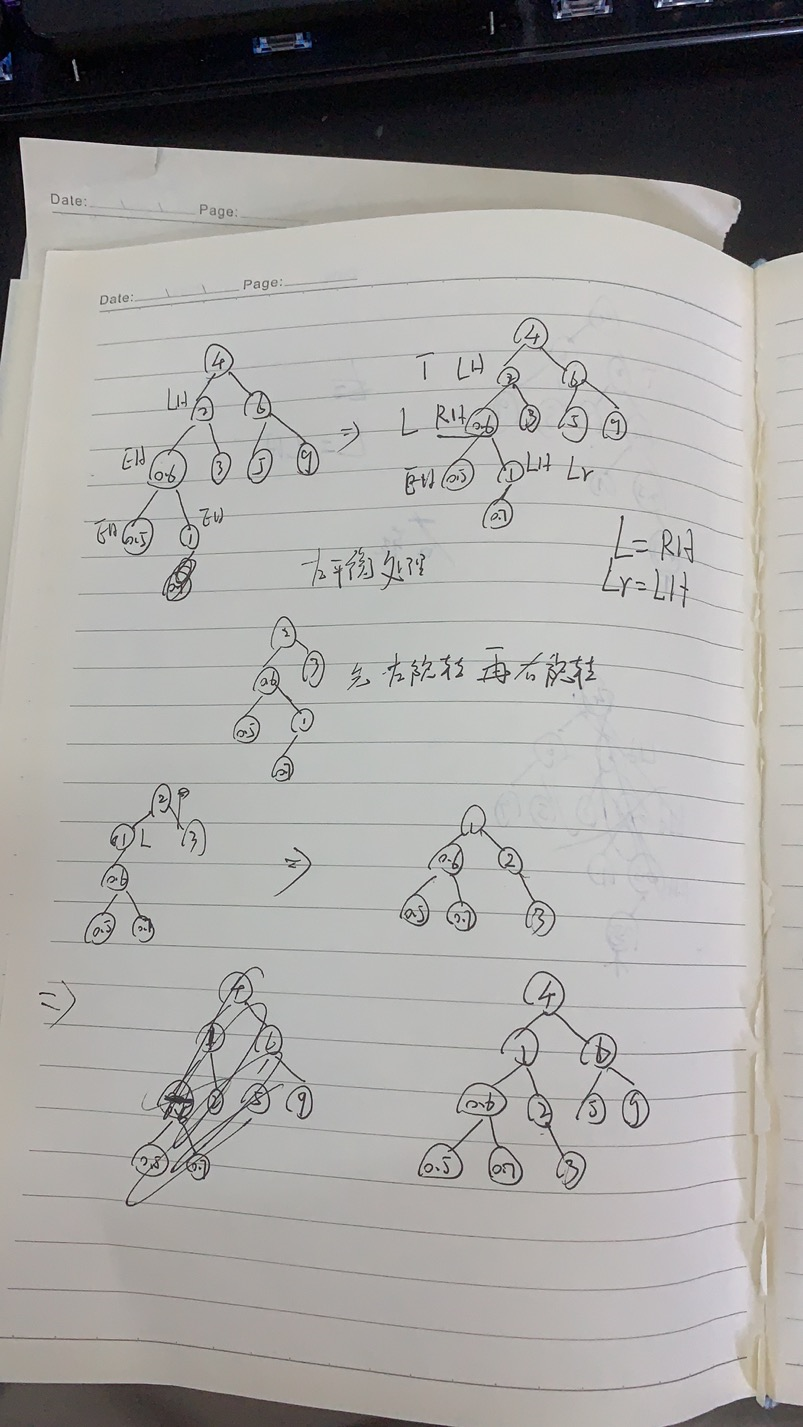
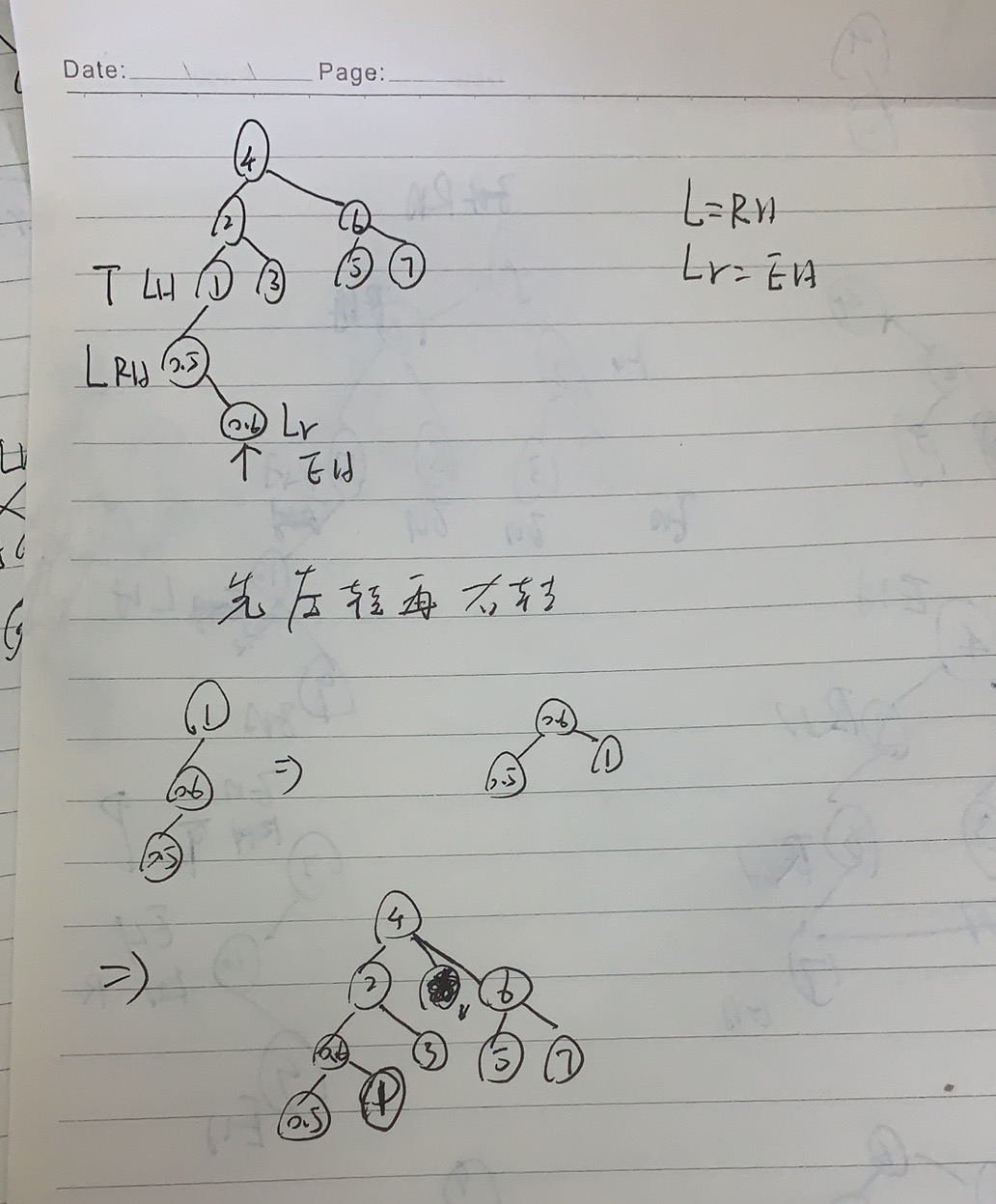
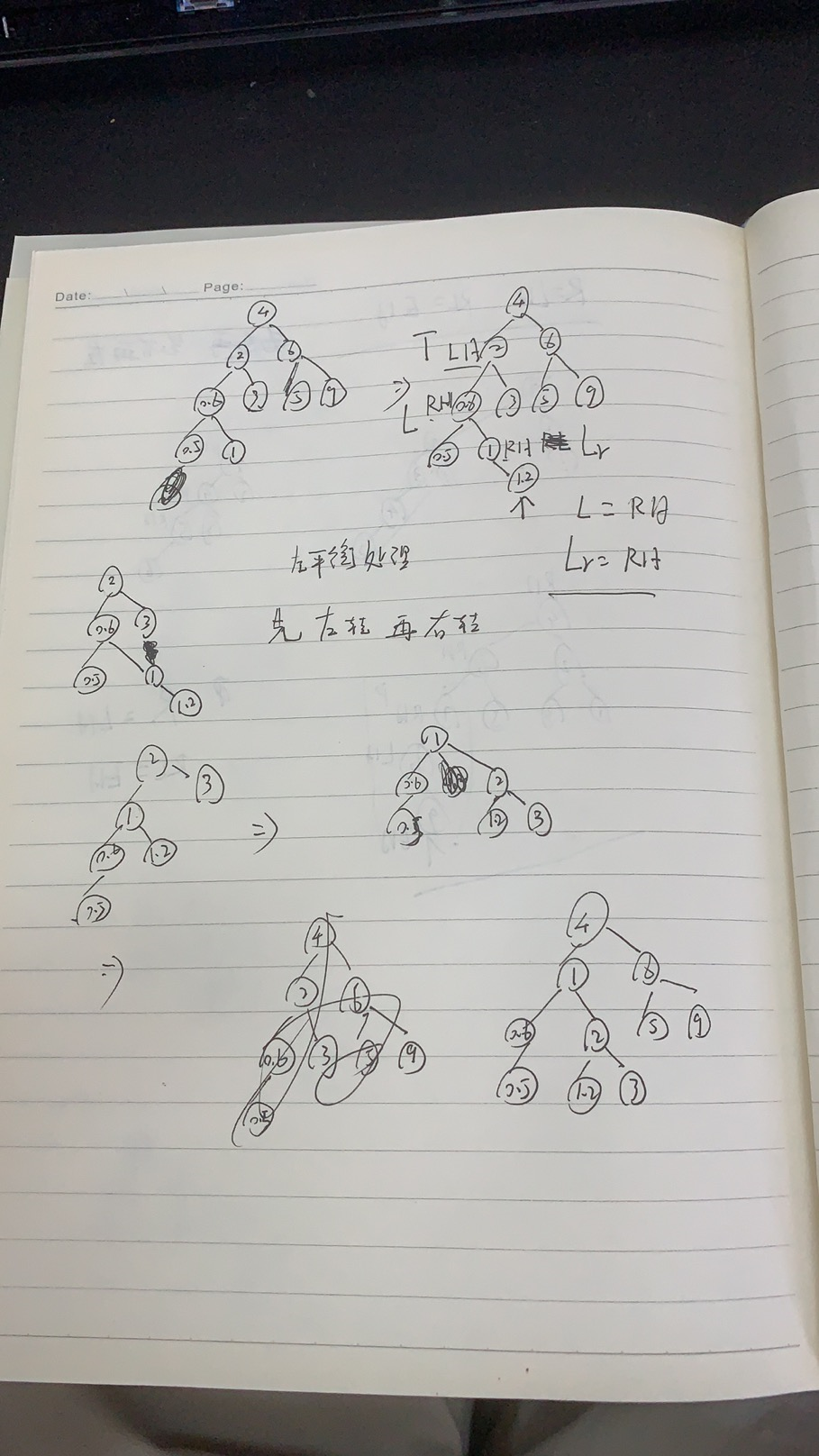
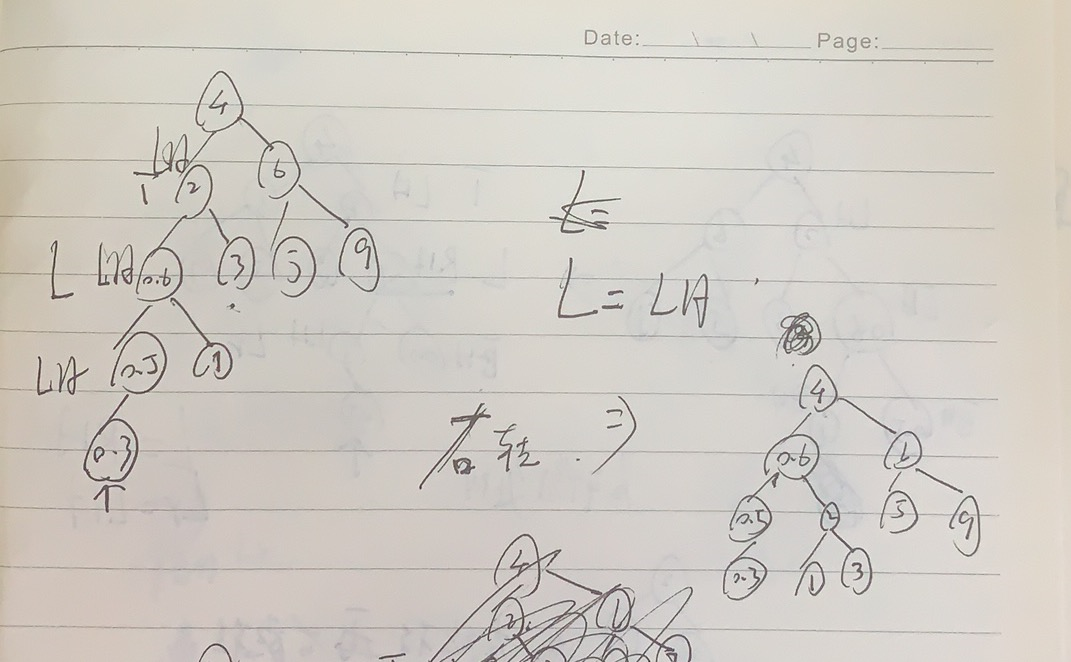
This section is quite brain burning. I finally understand!
m-way search trees

2-3 tree
2-3 trees either have two children. Or no children
2-3 tree with two nodes and three nodes
Insertion principle
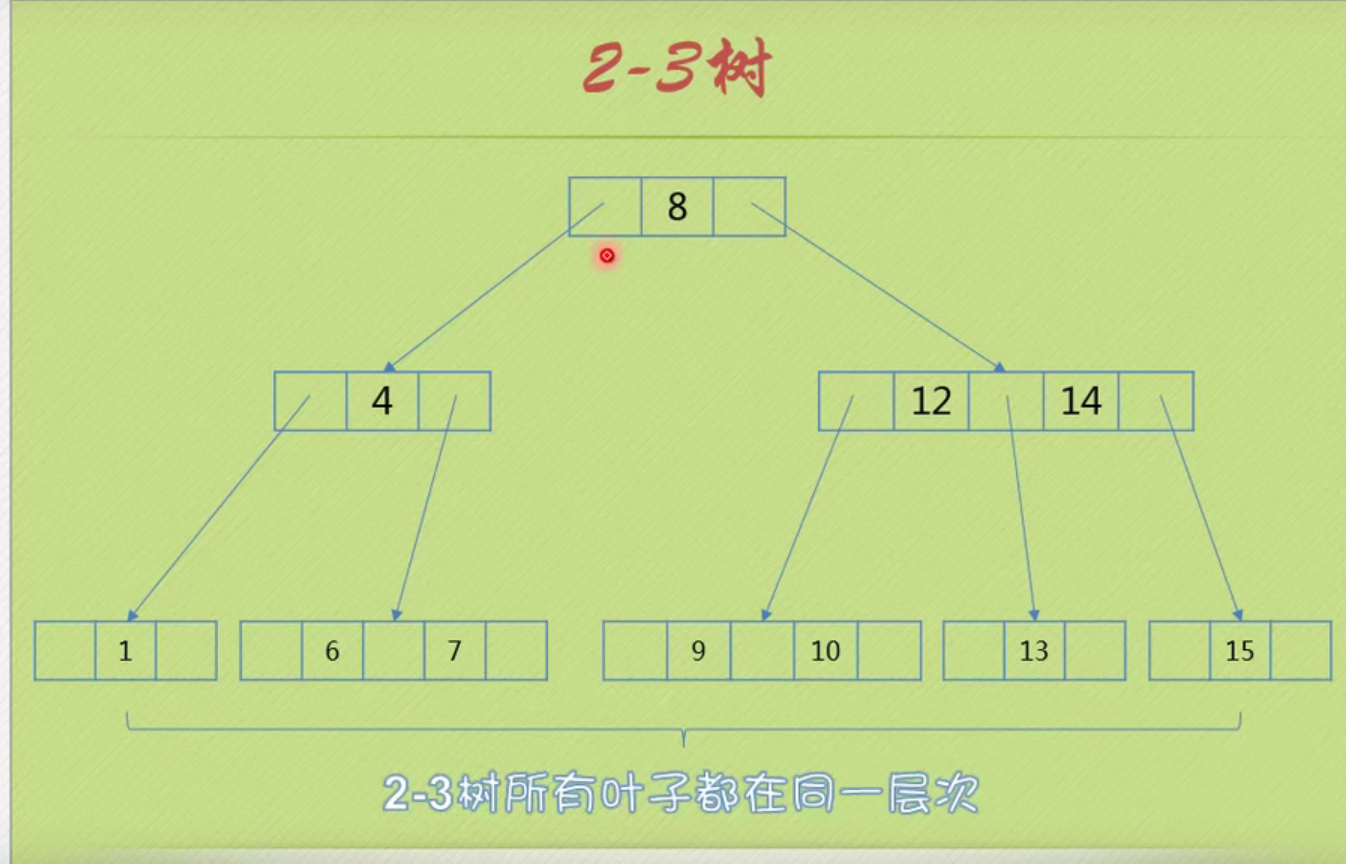
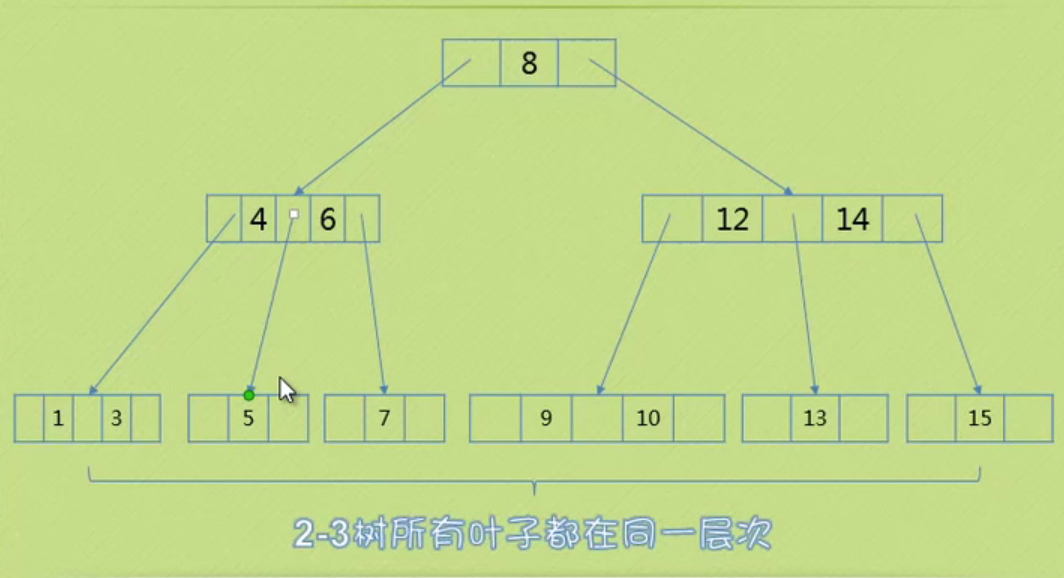
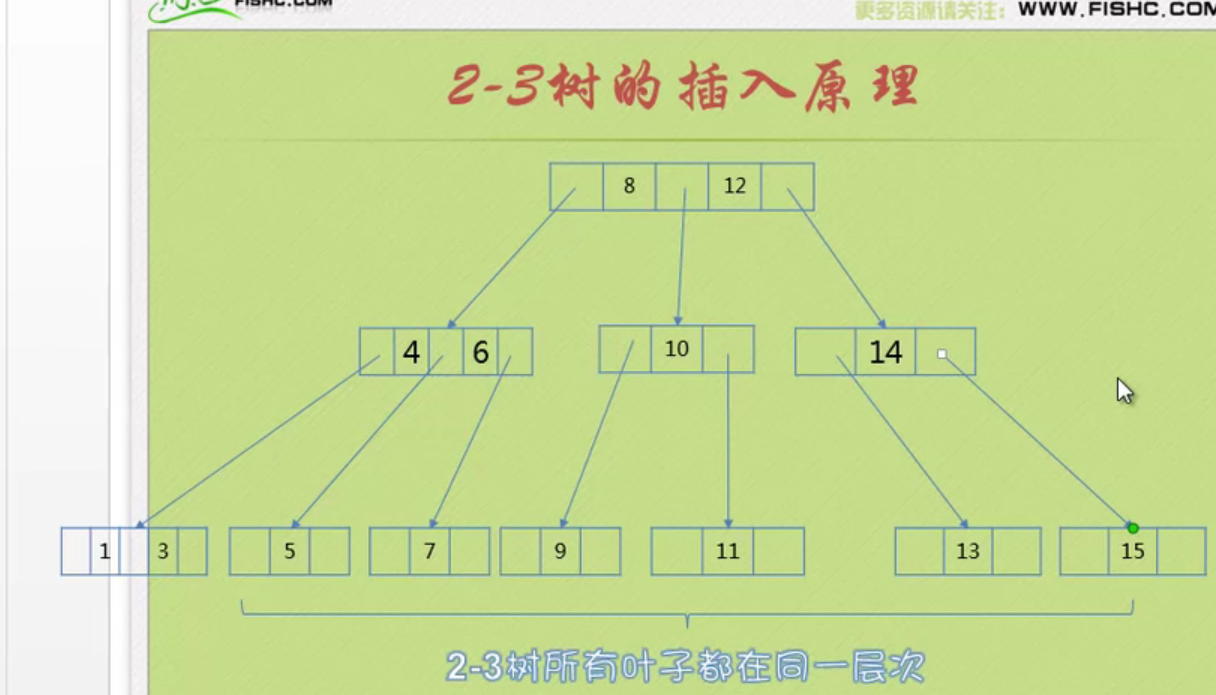
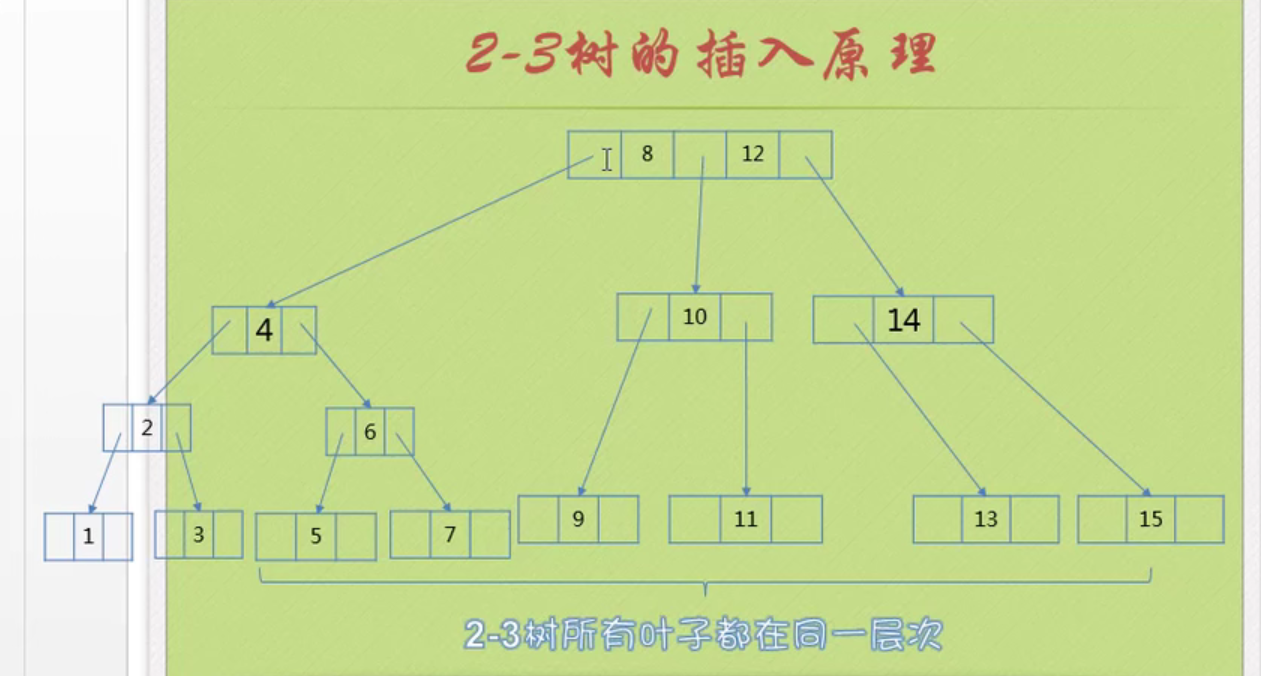
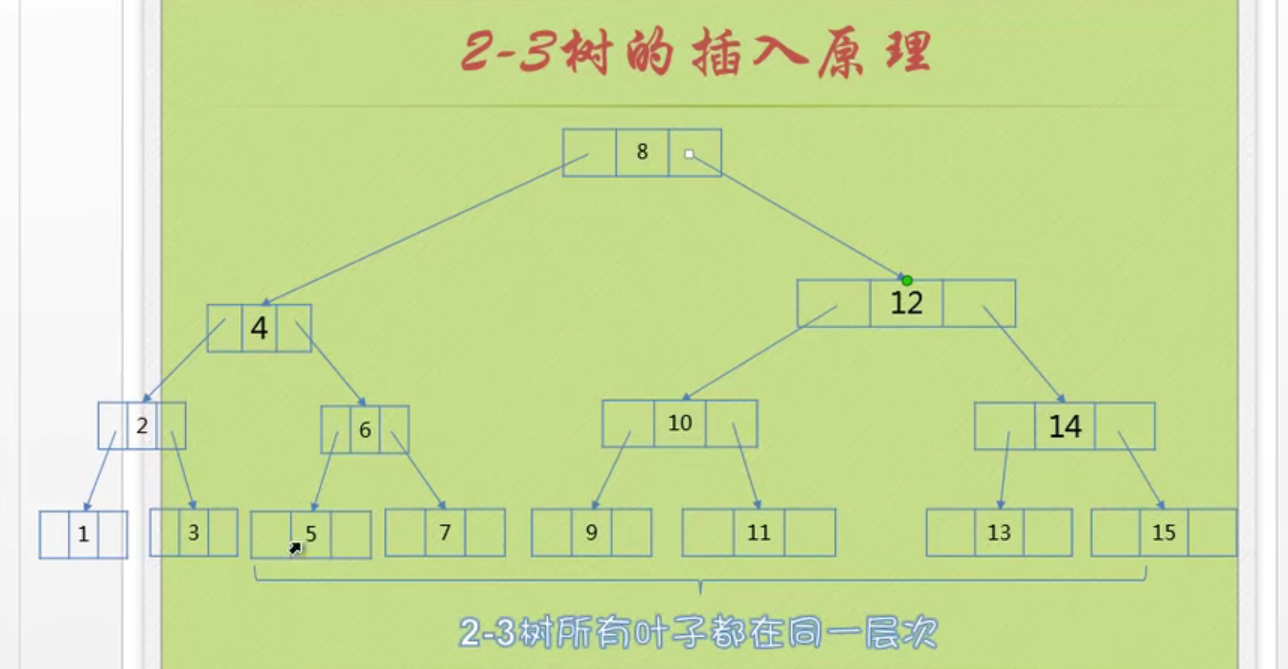
In the first case, if it is an empty tree, insert two nodes directly, that is, the root node
In the second case, it is inserted into a two node, and the two nodes become three nodes
The third situation is more complex:
When the inserted leaf is a three node, the leaf parent It is a two node, which inserts new data by expanding its parents When the inserted leaf is a three node, the leaf parent It's three nodes. Go find it parent of parent ,have a look parent of parent Is it a two node, can it be extended When the inserted leaf is a three node, the leaf parent It's three nodes. Go find it parent of parent ,Tracing back to the root node, if the root node is still three nodes, we need to increase the height of the tree,
Delete principle
Delete leaf node
1, If the leaf to be deleted is an element in three nodes, it is very simple to delete one of the three nodes and turn it into two nodes
For example, in the figure below, you have to delete 6
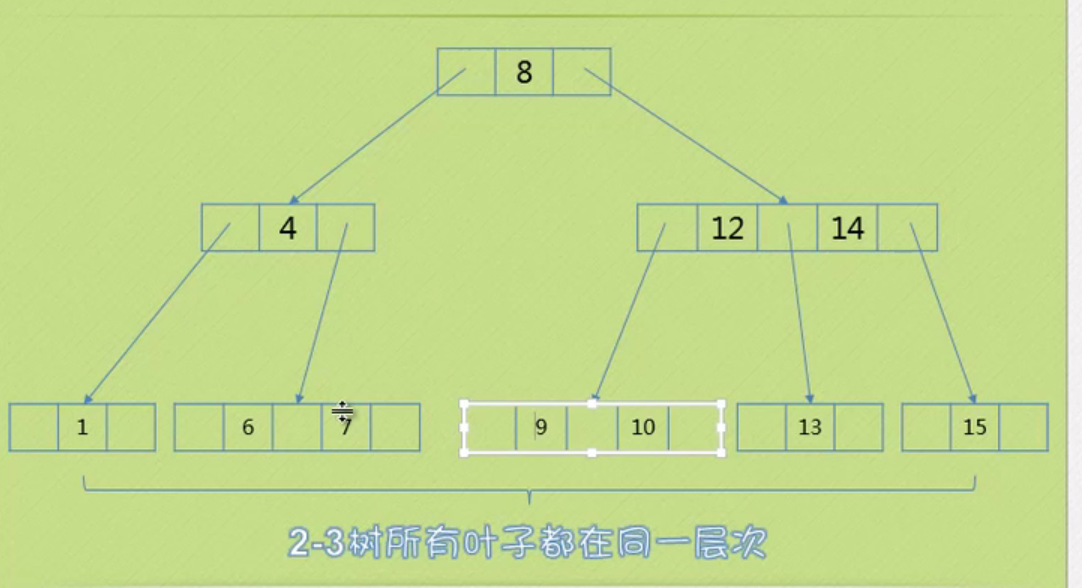
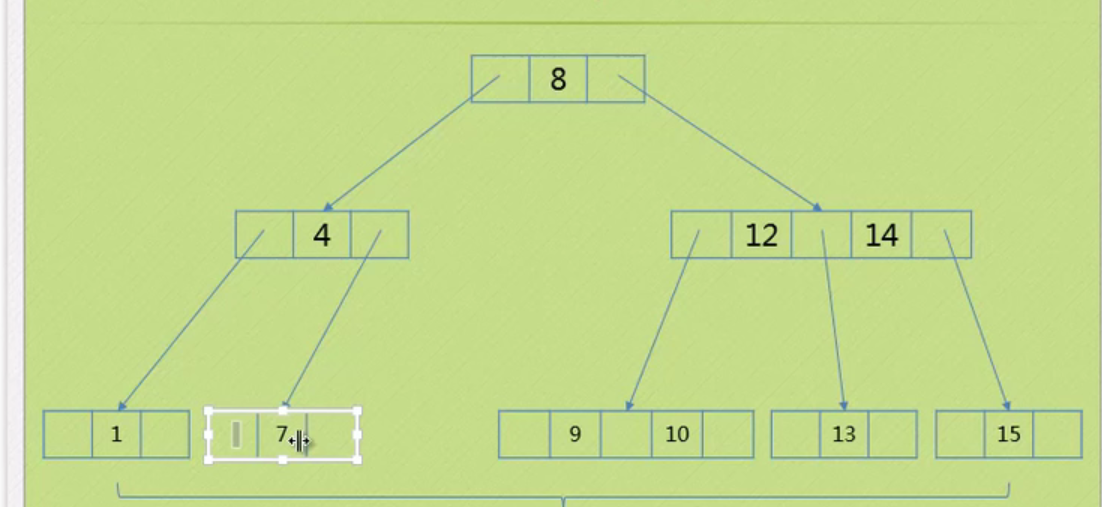
2, The deleted element is located on the second node
1. First case
The parent of this two node is also a two node, and the other child of this parent is a three node
As shown in the figure below, element 1
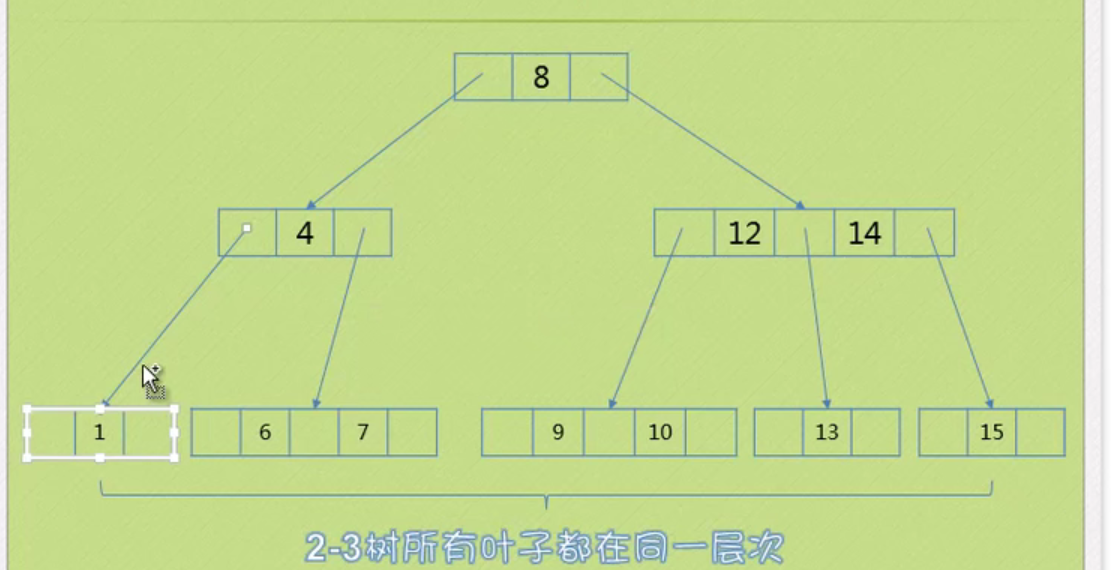
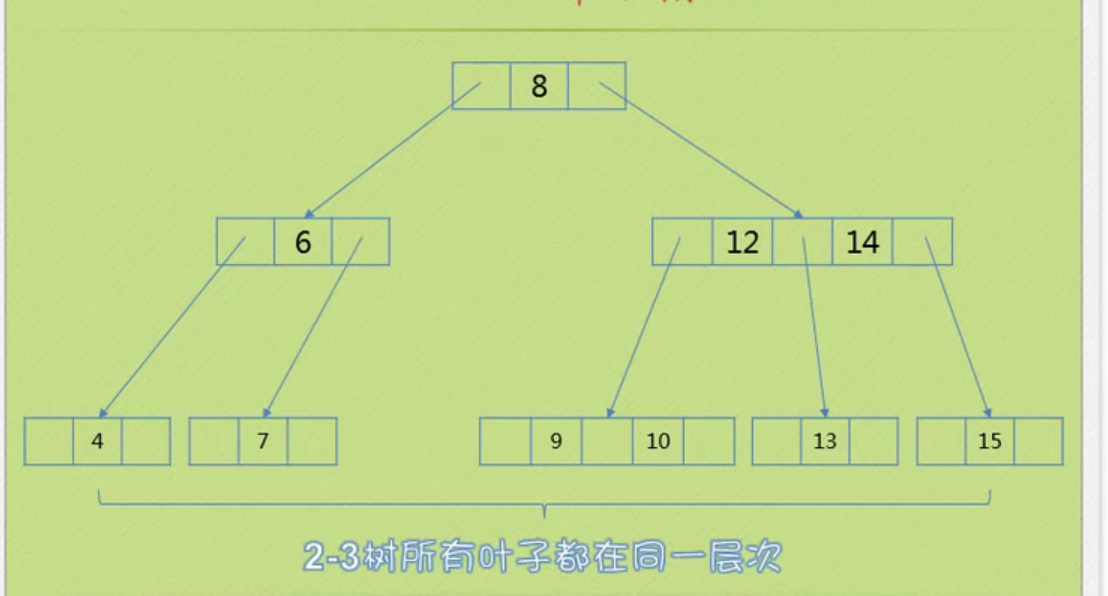
2. The second case
This two node parent is two node, and the other child of the two parents is also two node
See element 4 below
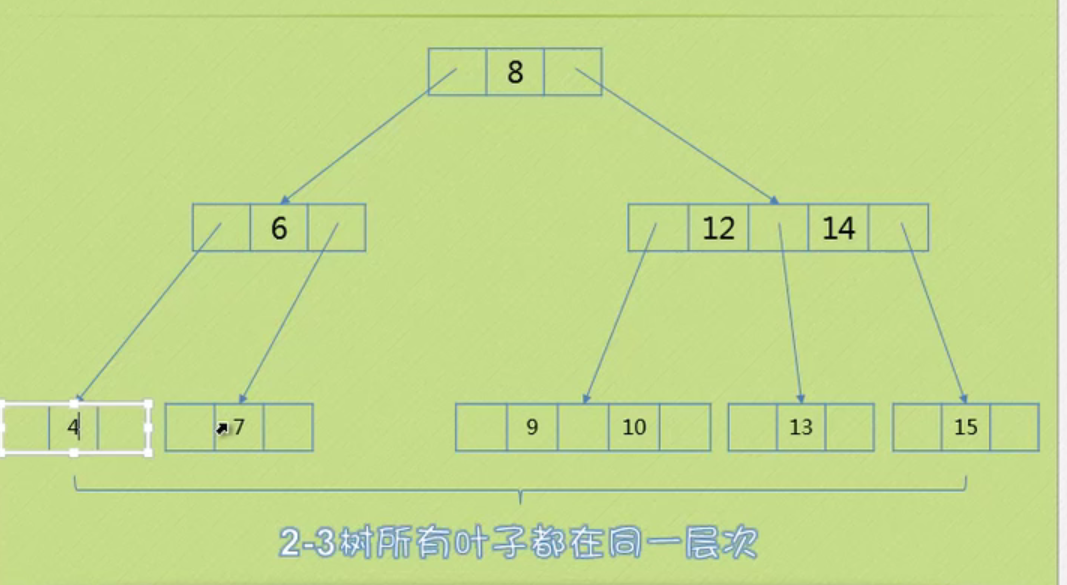
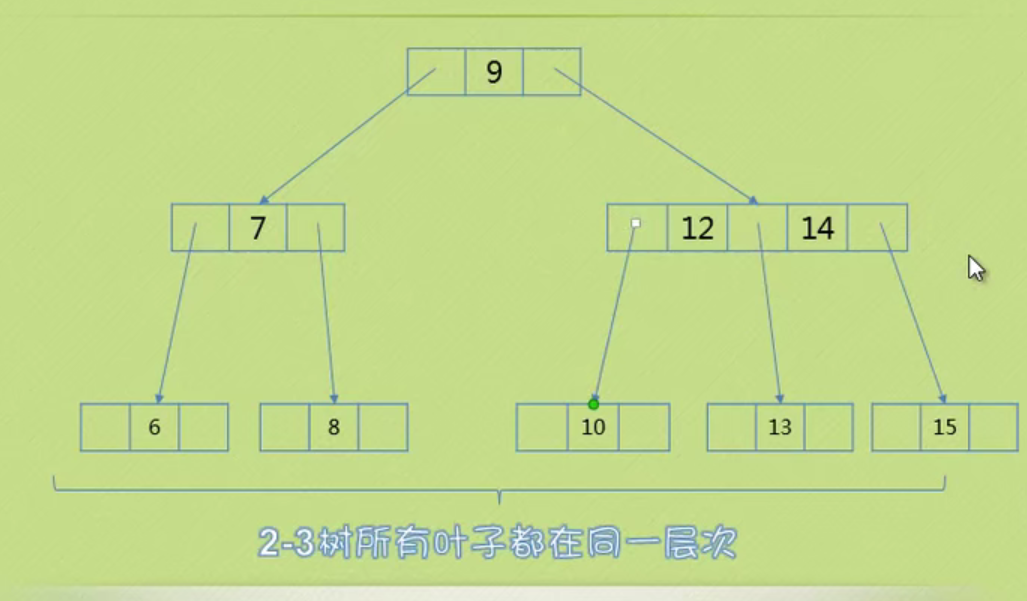
3. The third case
The parents of this two node are three nodes
See element 10 in the figure below
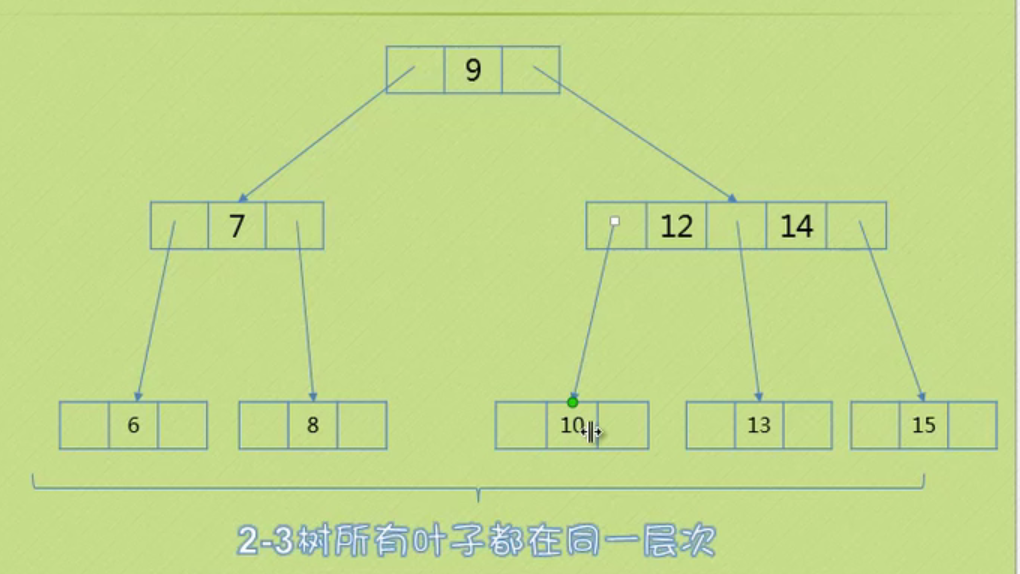
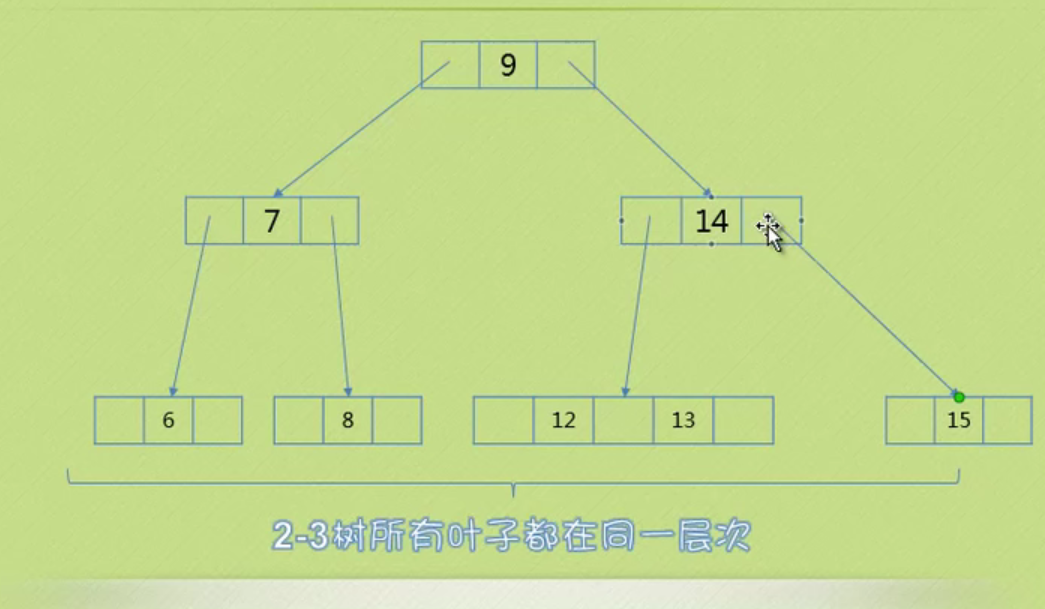
3, In the case of full binary tree, all nodes are binary nodes
See element 8 in the figure below
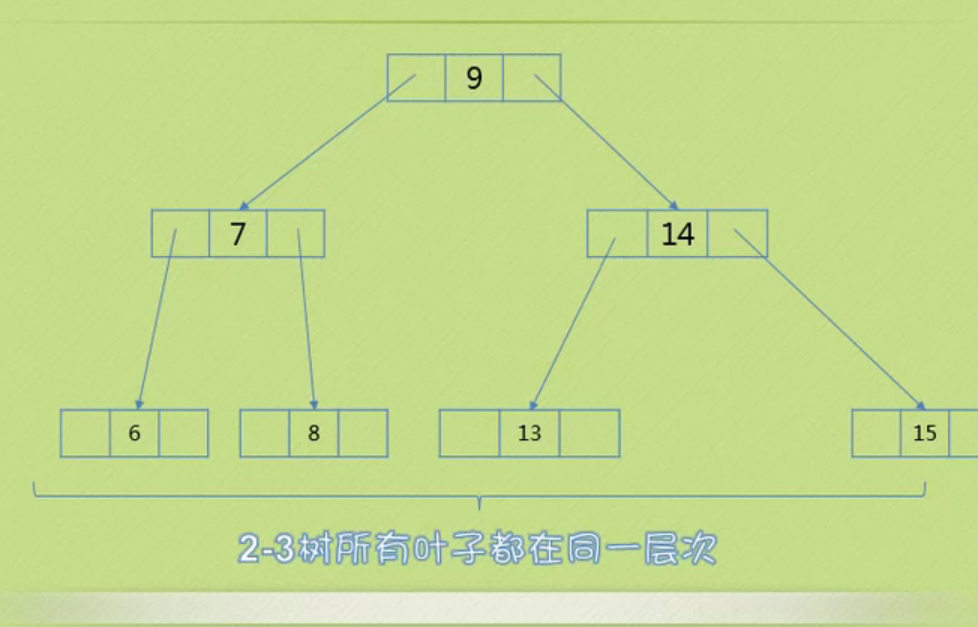
Reduce one layer to three nodes
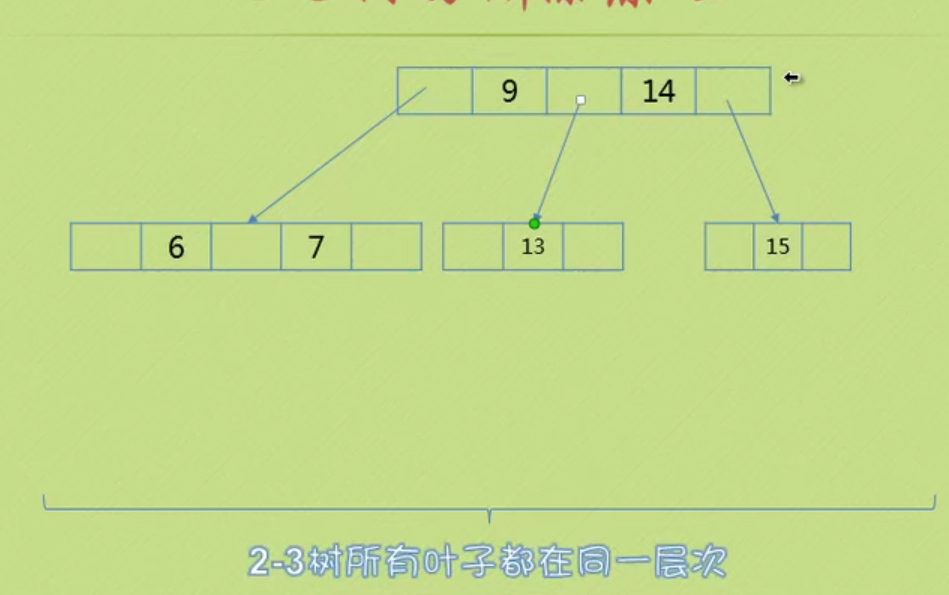
Delete non leaf nodes
1, The second node is deleted. Children have three nodes
See element 4 below
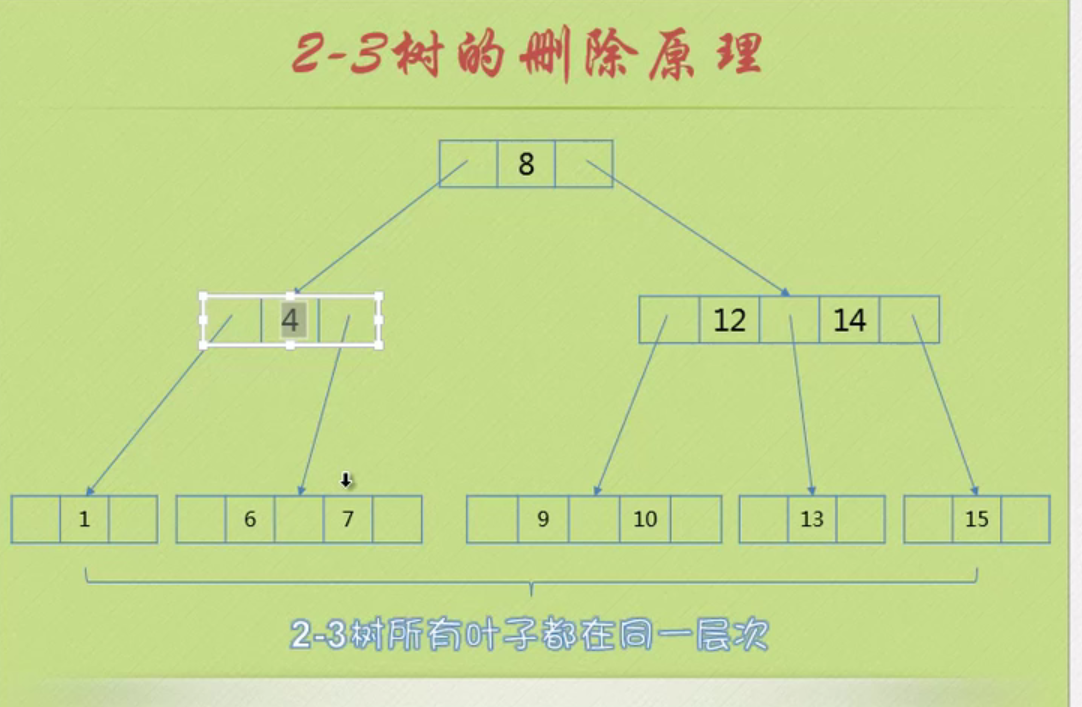
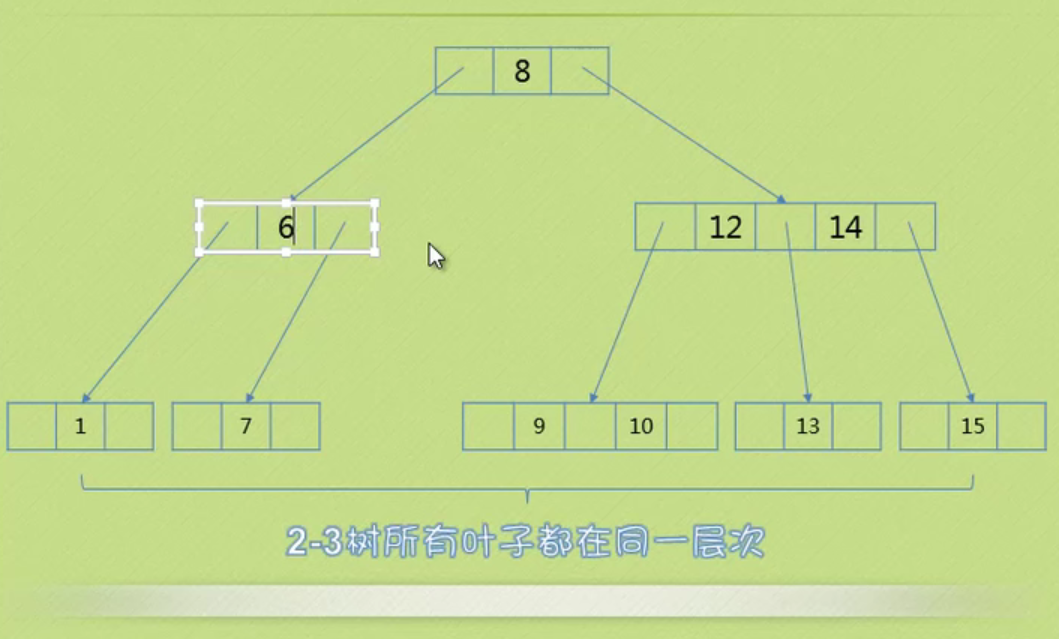
2, The deleted element has a three node child at three nodes
See element 12 in the figure below

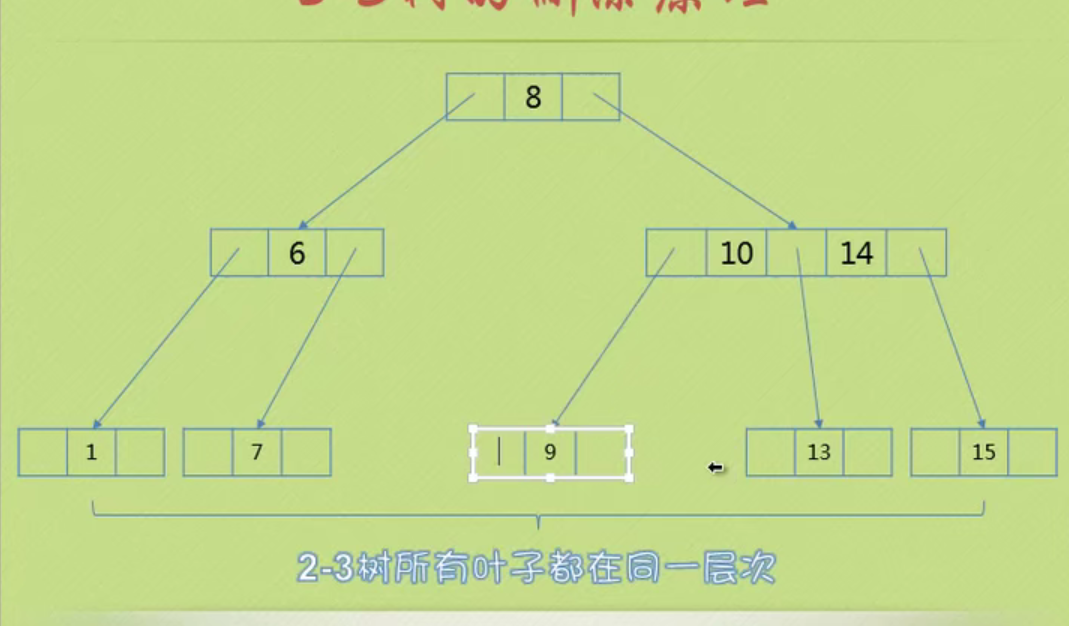
Generally speaking, these deletion principles are relatively simple, but there are many situations to consider
2-3-4 tree
Either two nodes, or three nodes, or four nodes
insert
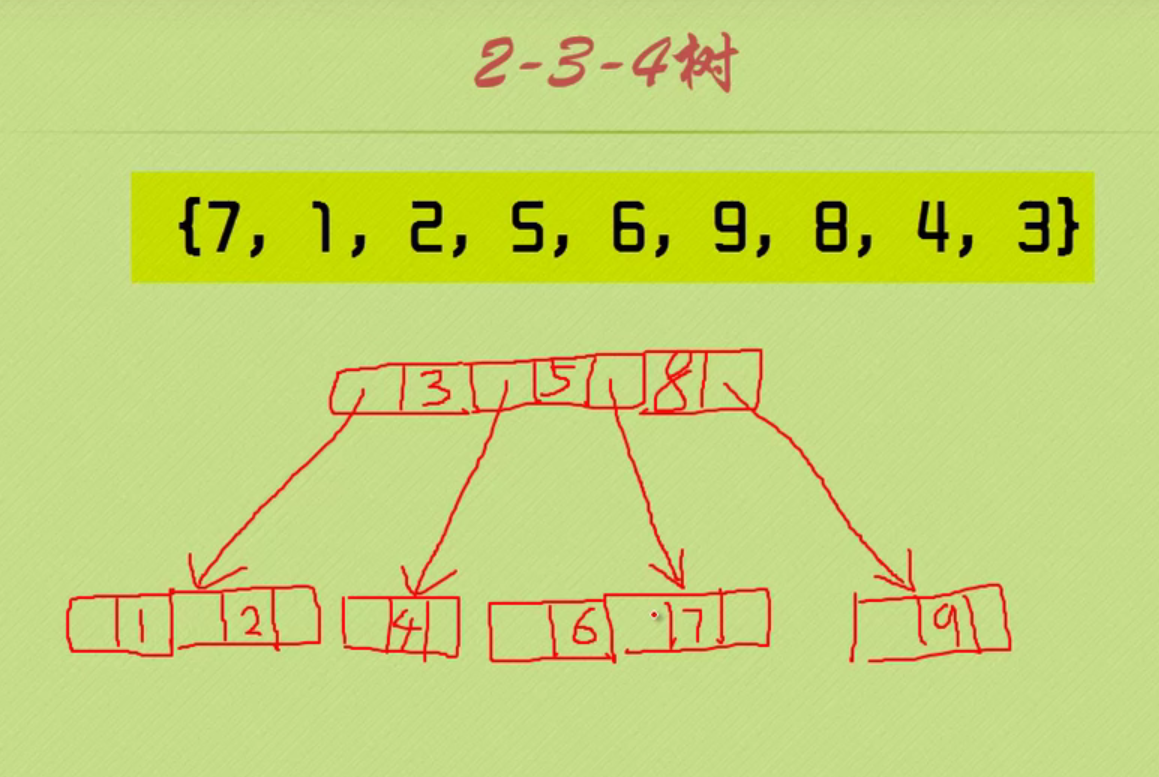
delete
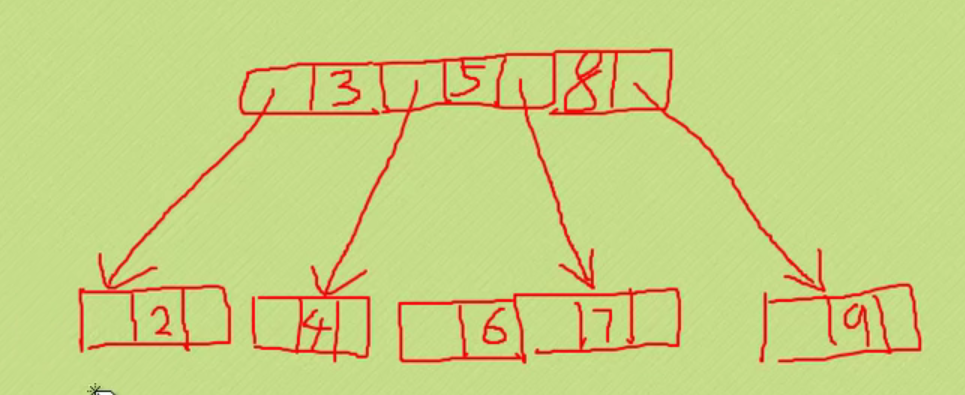
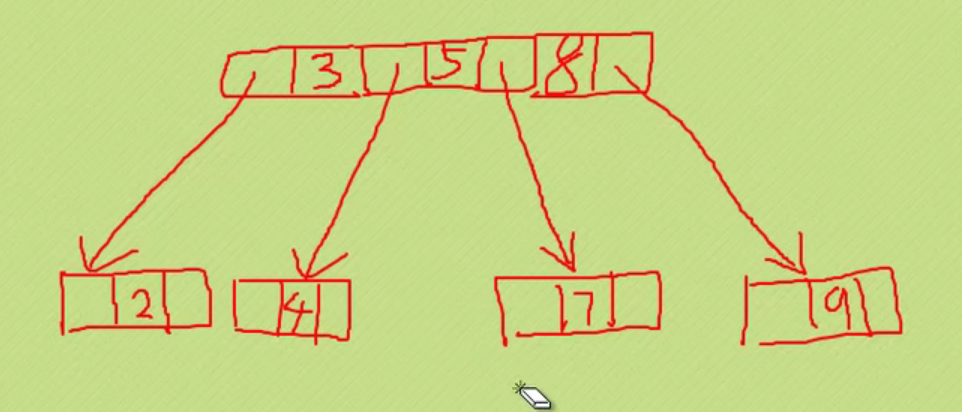
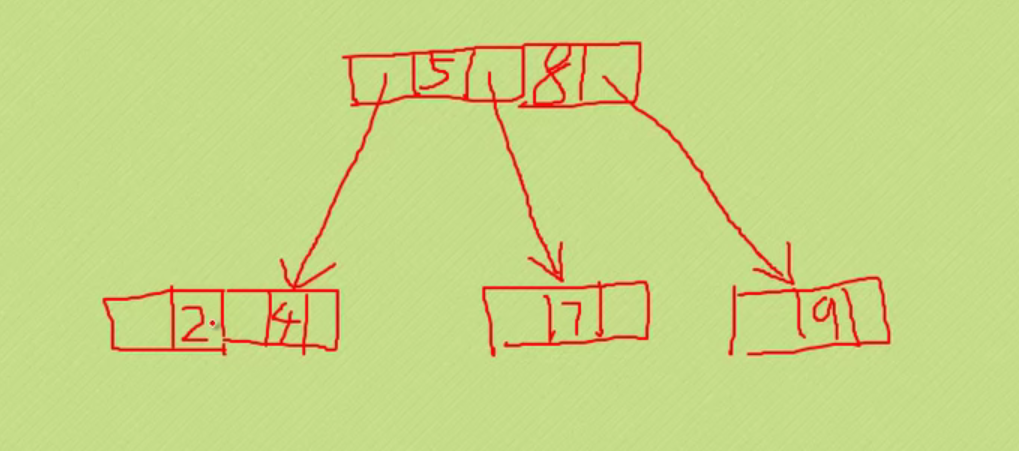
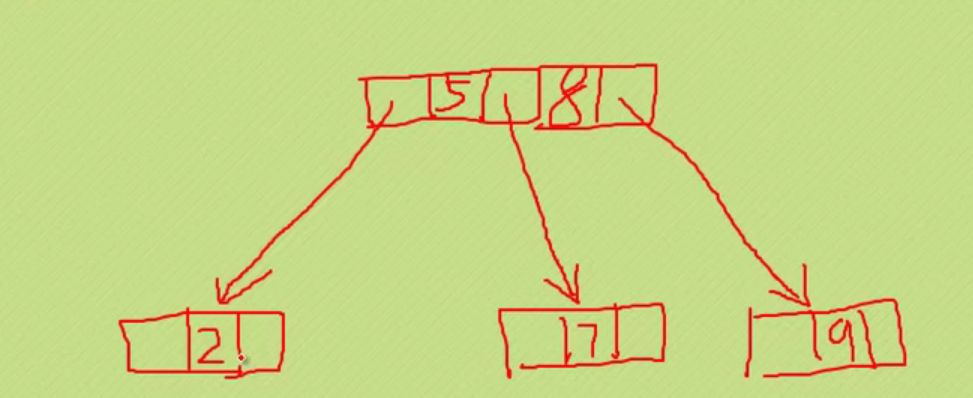
B tree

nature

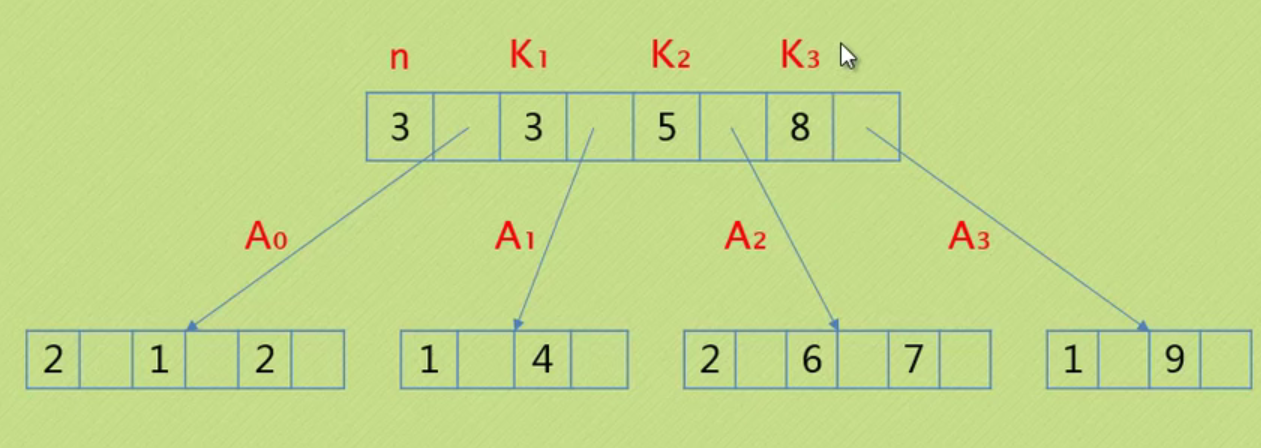
Hash table lookup



Construction method

Direct address method
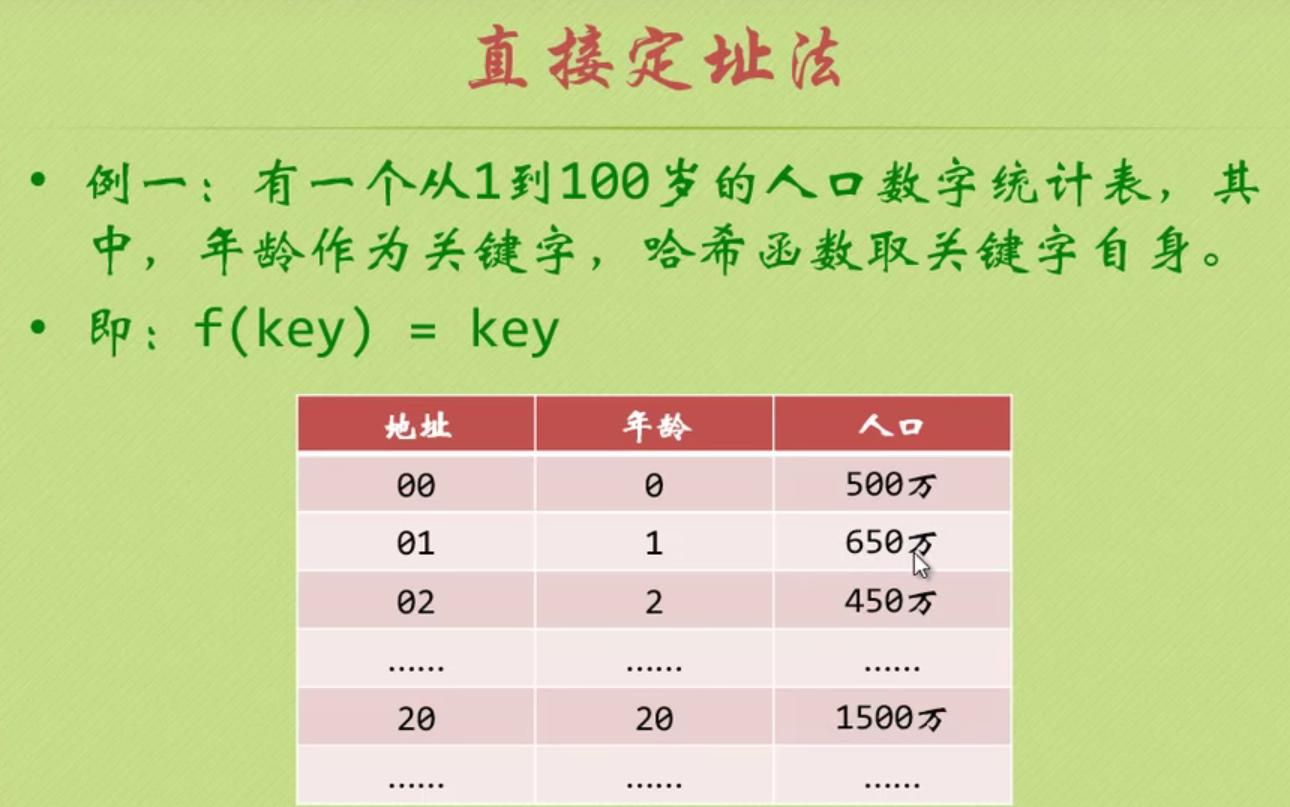
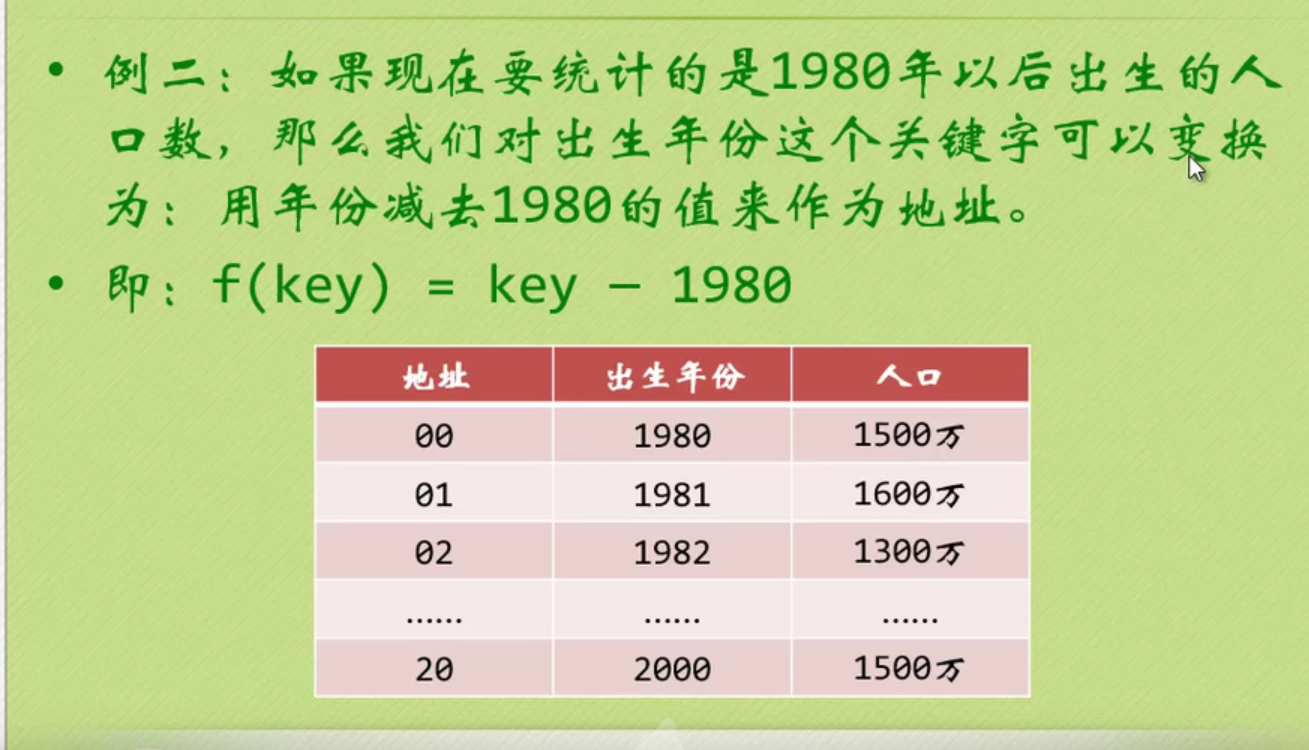

It is to use the key and then linearly calculate the key to obtain the address. It is the direct address method. It is not commonly used
Digital analysis
It is suitable for dealing with large numbers
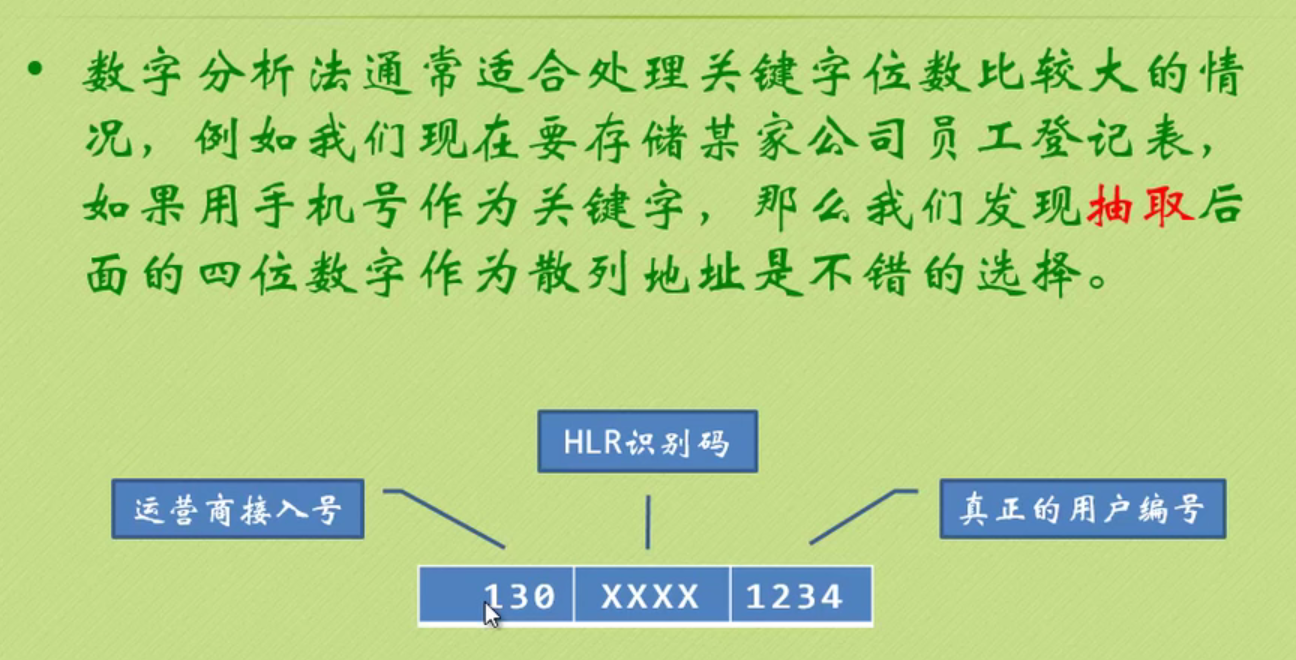
Square middle method
It is suitable for dealing with the situation that the distribution of keywords is unknown and the number of digits is not very large

Folding method
Do not know the distribution of keywords in advance, which is suitable for the situation with a large number of keywords

Residual tree method
Common methods


Random number method
It is suitable for different keyword lengths


Method for handling hash table conflict
Open address method



Re hash function method
Prepare more hash functions.

Chain address method
Using linked list
Mr. Hou Jie talked about the underlying implementation of STL and used it, like GUC4.9
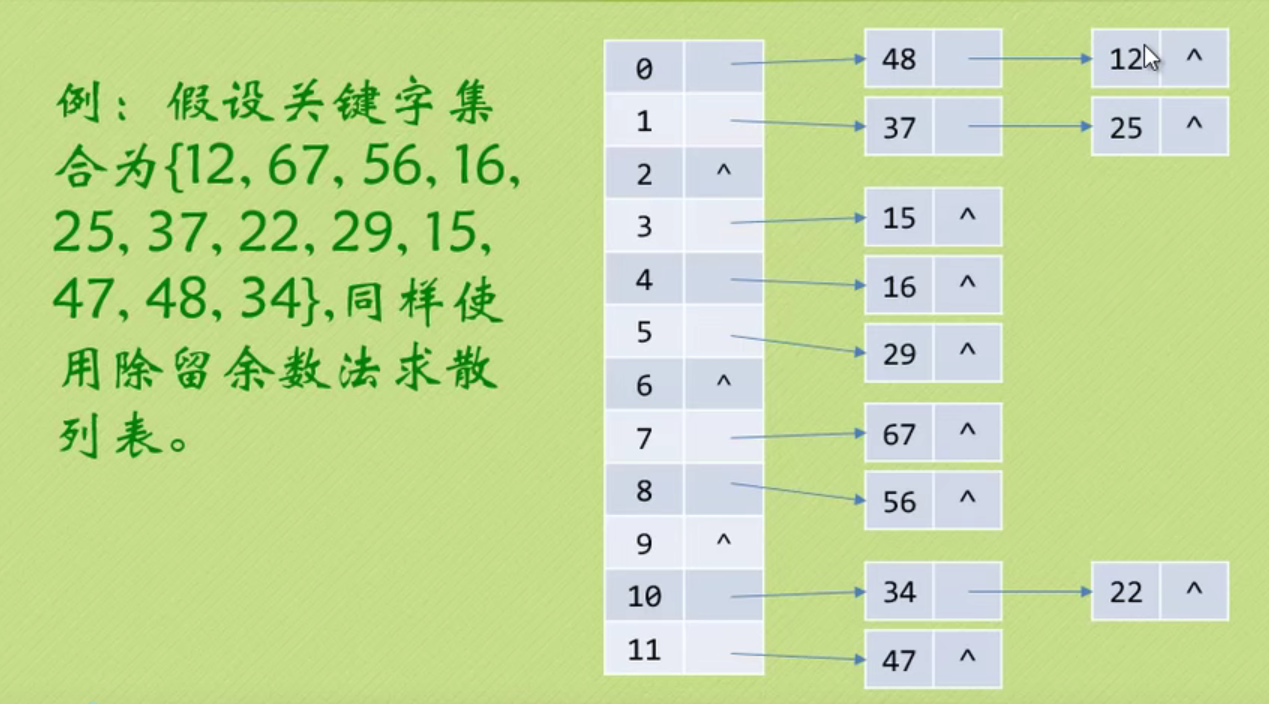
Public spillover area method
First check the basic table. If the basic table is not found, then find the overflow table
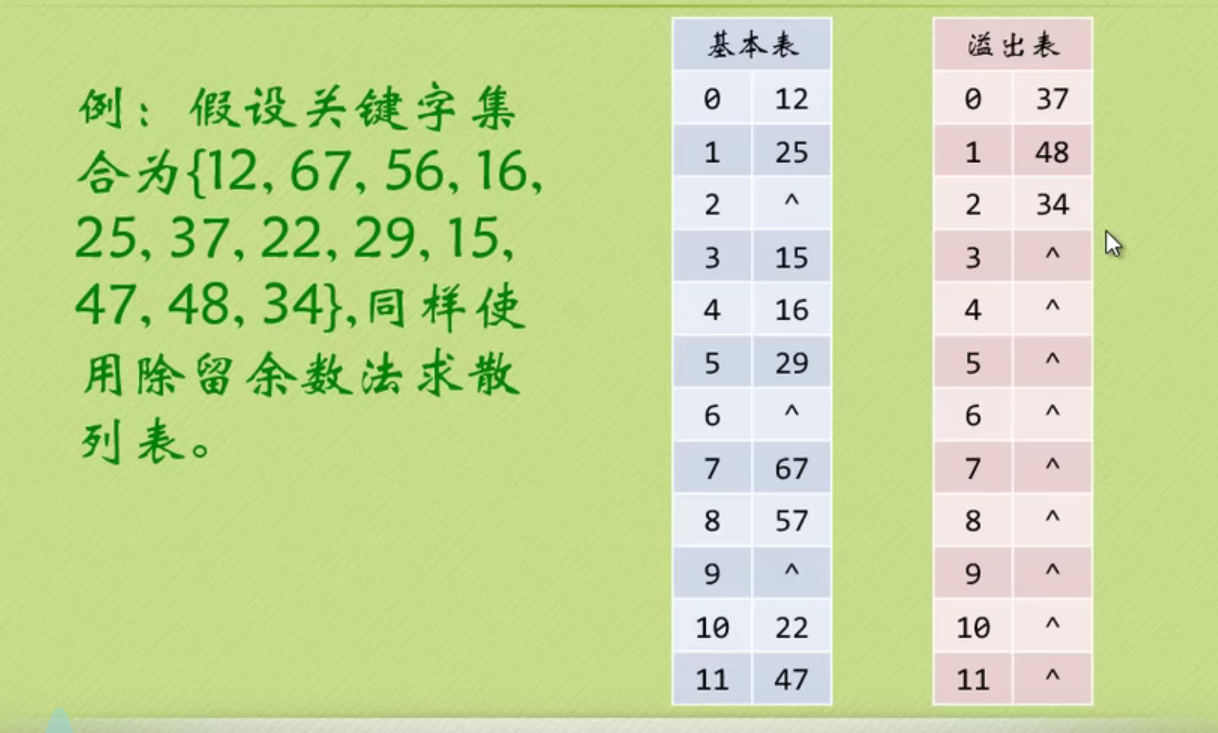
Hash table lookup code implementation
#include <iostream>
using namespace std;
#define HASHSIZE 12
#define NULLKEY -32768
typedef struct
{
int *elem;//Base address of data element, dynamically allocating array
int count;//Number of current data elements
}HashTable;
/**
* Hash table initialization
* @param H
* @return
*/
int InitHahTable(HashTable *H)
{
H->count=HASHSIZE;
H->elem=(int *) malloc(HASHSIZE*sizeof (int));
if(!H->elem)
{
return -1;
}
for(int i=0;i<HASHSIZE;i++)
{
H->elem[i]=NULLKEY;
}
return 0;
}
/**
* Division method
* @param key
* @return
*/
int Hash(int key)
{
return key% HASHSIZE;
}
/**
* Insert keyword into hash table
* @param H
* @param key
*/
void InsertHash(HashTable *H,int key)
{
int addr;
addr= Hash(key);
while(H->elem[addr]!=NULLKEY)//If it is not empty, a conflict occurs
{
//Open addressing
addr=(addr+1)%HASHSIZE;
}
H->elem[addr]=key;
}
/**
* Hash table lookup
* @param H
* @param key
* @param addr
* @return
*/
int SearchHash(HashTable H,int key,int *addr)
{
*addr= Hash(key);
while(H.elem[*addr]!=key)
{
*addr=(*addr+1)%HASHSIZE;
if(H.elem[*addr]==NULLKEY|| *addr == Hash(key))//Finding the last key or returning to the origin indicates that this key does not exist
{
return -1;
}
}
return 0;
}
/**
* Test hash table lookup
*/
void test_HashTable()
{
HashTable H;
InitHahTable(&H);
int c;
int inputKey;
cout<<"Enter inserted key: (12 individual)"<<endl;
for(int i=0;i<HASHSIZE;i++)
{
cin>>inputKey;
InsertHash(&H,inputKey);
}
cout<<"Please enter the number you want to find:('#'end search) "< < endl;
cin>>c;
while(c!=-32768)
{
int key=c;
cout<<key<<": ";
int add;
if(SearchHash(H,key,&add))
{
cout<<"No such number!"<<endl;
}
else
{
cout<<"Search succeeded!"<<endl;
cout<<"Address:"<<add<<endl;
}
cout<<"Please enter the number you want to find:('#'end search) "< < endl;
cin>>c;
}
}
int main() {
test_HashTable();
return 0;
}
Operation results:
Enter inserted key: (12 individual)
1
2
3
4
5
6
7
8
9
10
11
16
Please enter the number you want to find:('#'end search'
16
16: Search succeeded!
Address: 0
Please enter the number you want to find:('#'end search'
4
4: Search succeeded!
Address: 4
Please enter the number you want to find:('#'end search'
12
12: No such number!
Please enter the number you want to find:('#'end search'
Sorting algorithm


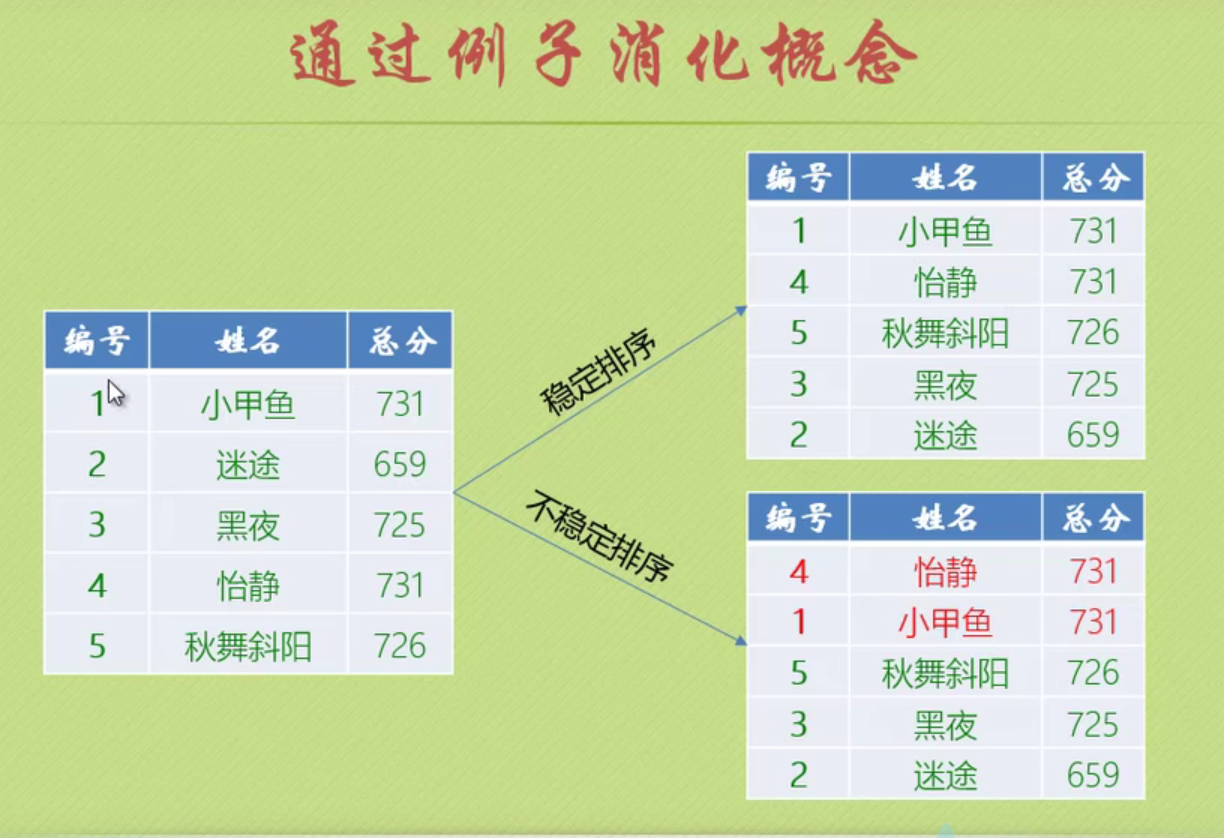
Bubble sorting

#include <iostream>
using namespace std;
/**
* In fact, this is not an authentic bubble sort. The real bubble sort should be two adjacent comparisons
* This sort is not an adjacent comparison
* @param k
* @param n
*/
void BubbleSort(int k[],int n)
{
int i,j,temp,count1=0,count2=0;
for(i=0;i<n-1;i++)
{
for(j=i+1;j<n;j++)
{
count1++;
if(k[i]>k[j])
{
count2++;
temp=k[j];
k[j]=k[i];
k[i]=temp;
}
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
/**
* Authentic bubble sorting
*/
void TrueBubbleSort(int k[],int n)
{
int i,j,temp,count1=0,count2=0;
for(i=0;i<n-1;i++)
{
for(j=n-1;j>i;j--)
{
count1++;
if(k[j-1]>k[j])
{
count2++;
temp=k[j-1];
k[j-1]=k[j];
k[j]=temp;
}
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
/**
* Authentic bubble sorting plus a little optimization plus a fall
*/
void TrueBubbleSortImproved(int k[],int n)
{
int i,j,temp,count1=0,count2=0,flag=1;
for(i=0;i<n-1 && flag;i++)
{
for(j=n-1;j>i;j--)
{
count1++;
flag=0;
if(k[j-1]>k[j])
{
count2++;
temp=k[j-1];
k[j-1]=k[j];
k[j]=temp;
flag=1;
}
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
int main() {
int i,a[10]={1,0,2,3,4,5,6,7,8,9};
//BubbleSort(a,10);
//TrueBubbleSort(a,10);
TrueBubbleSortImproved(a,10);//
for(int i=0;i<10;i++)
{
cout<<a[i];
}
cout<<endl;
return 0;
}
Operation results
Bubble sorting************************** How many comparisons were made in total: 45 How many moves were made in total: 1 0123456789 Bubble sorting************************** Authentic bubble sorting plus flag optimization************************** How many comparisons were made in total: 17 How many moves were made in total: 1 0123456789 Authentic bubble sorting plus flag optimization**************************
Select sort

#include <iostream>
using namespace std;
/**
* Select sort
* @param a
* @param n
*/
void ChooseSort(int a[],int n)
{
int min,temp,count1=0,count2=0;
for(int i=0;i<n-1;i++)
{
min=i;
for(int j=i+1;j<n;j++)
{
count1++;
if(a[j]<a[min])
{
min=j;
}
}
if(min!=i)
{
count2++;
temp=a[min];
a[min]=a[i];
a[i]=temp;
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
void testChoose()
{
cout<<"Select sort**************************"<<endl;
int a[10]={5,2,6,0,3,9,1,7,4,8};
ChooseSort(a,10);
for(int i=0;i<10;i++)
{
cout<<a[i];
}
cout<<endl;
cout<<"Select sort**************************"<<endl;
}
/**
* Authentic bubble sorting plus a little optimization plus a fall
*/
void TrueBubbleSortImproved(int k[],int n)
{
int i,j,temp,count1=0,count2=0,flag=1;
for(i=0;i<n-1 && flag;i++)
{
for(j=n-1;j>i;j--)
{
count1++;
flag=0;
if(k[j-1]>k[j])
{
count2++;
temp=k[j-1];
k[j-1]=k[j];
k[j]=temp;
flag=1;
}
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
void testBubble()
{
cout<<"Authentic bubble sorting plus flag optimization**************************"<<endl;
int a[10]={5,2,6,0,3,9,1,7,4,8};
//BubbleSort(a,10);
//TrueBubbleSort(a,10);
TrueBubbleSortImproved(a,10);
for(int i=0;i<10;i++)
{
cout<<a[i];
}
cout<<endl;
cout<<"Authentic bubble sorting plus flag optimization**************************"<<endl;
}
int main() {
testChoose();
testBubble();
return 0;
}
Operation results
Select sort************************** How many comparisons were made in total: 45 How many moves were made in total: 7 0123456789 Select sort************************** Authentic bubble sorting plus flag optimization************************** How many comparisons were made in total: 39 How many moves were made in total: 17 0123456789 Authentic bubble sorting plus flag optimization**************************
Direct insert sort

#include <iostream>
using namespace std;
void InsertSort(int a[],int n)
{
int i,j,temp,count1=0,count2=0;
for(i=1;i<n;i++)
{
count1++;
if(a[i]<a[i-1])
{
temp=a[i];//Set up sentry
for(j=i-1;a[j]>temp&& j>=0;j--)
{
count2++;
a[j+1]=a[j];
}
a[j+1]=temp;
}
}
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
void testInsert()
{
cout<<"Direct insert sort**************************"<<endl;
int a[10]={5,2,6,0,3,9,1,7,4,8};
InsertSort(a,10);
for(int i=0;i<10;i++)
{
cout<<a[i];
}
cout<<endl;
cout<<"Direct selection sort**************************"<<endl;
}
int main() {
testInsert();
return 0;
}
Operation results
Direct insert sort************************** How many comparisons were made in total: 9 How many moves were made in total: 17 0123456789 Direct selection sort**************************
Shell Sort

Before that, the time complexity was O(n2)
The time complexity of hill sorting is:

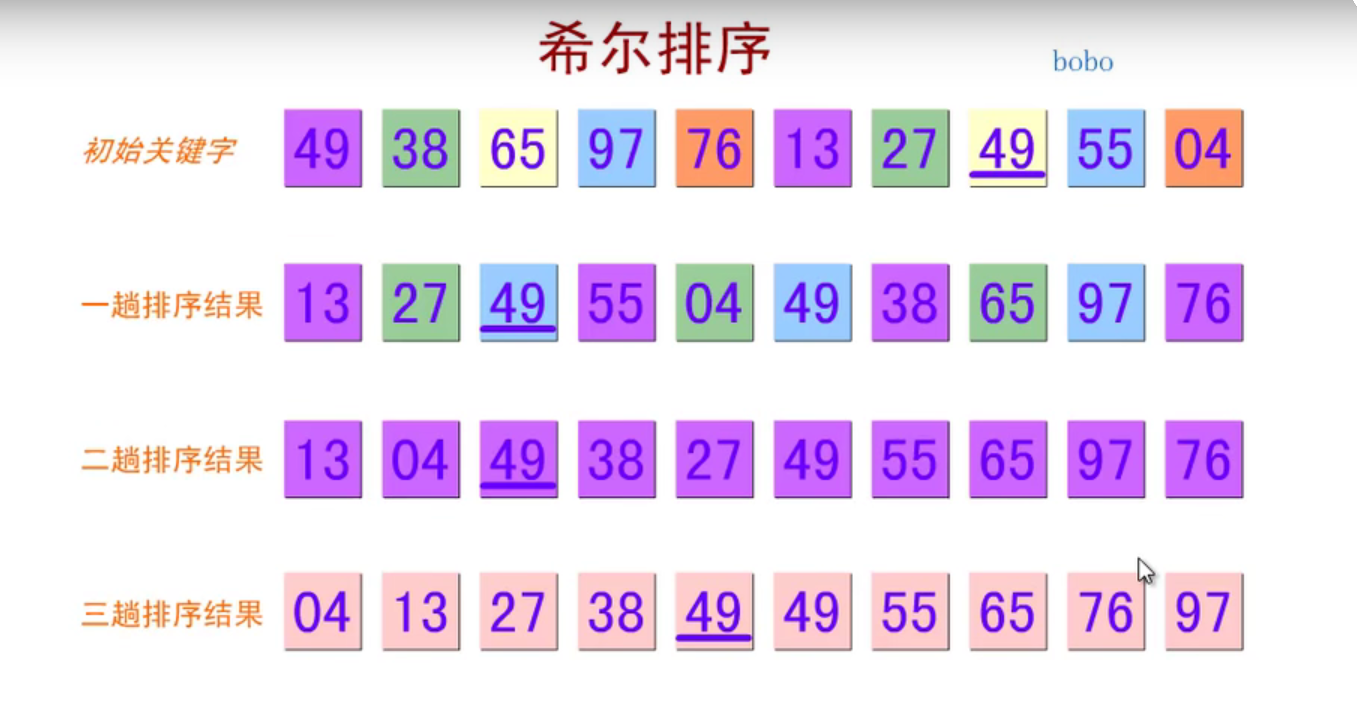
The interval between two comparisons is different
#include <iostream>
using namespace std;
void ShellSort(int a[],int n)
{
//{5,2,6,0,3,9,1,7,4,8}
int i,j,temp,count1=0,count2=0;
int gap=n;
do
{
gap=gap/3 ;
for(i=gap;i<n;i++)
{
count1++;
if(a[i]<a[i-gap])
{
temp=a[i];//Set up sentry
for(j=i-gap;a[j]>temp&& j>=0;j-=gap)
{
count2++;
a[j+gap]=a[j];
}
a[j+gap]=temp;
}
}
}while(gap>1);
cout<<"How many comparisons were made in total: "<<count1<<"How many moves were made in total: "<<count2<<endl;
}
void testShell()
{
cout<<"Shell Sort **************************"<<endl;
int a[10]={5,2,6,0,3,9,1,7,4,8};
ShellSort(a,10);
for(int i=0;i<10;i++)
{
cout<<a[i];
}
cout<<endl;
cout<<"Shell Sort **************************"<<endl;
}
int main() {
testShell();
return 0;
}
Operation results
Shell Sort ************************** How many comparisons were made in total: 16 How many moves were made in total: 9 0123456789 Shell Sort **************************
Heap sort
principle
Improved selection sorting
A complete binary tree is one in which the last layer is satisfied from right to left and the leaves are not vacant
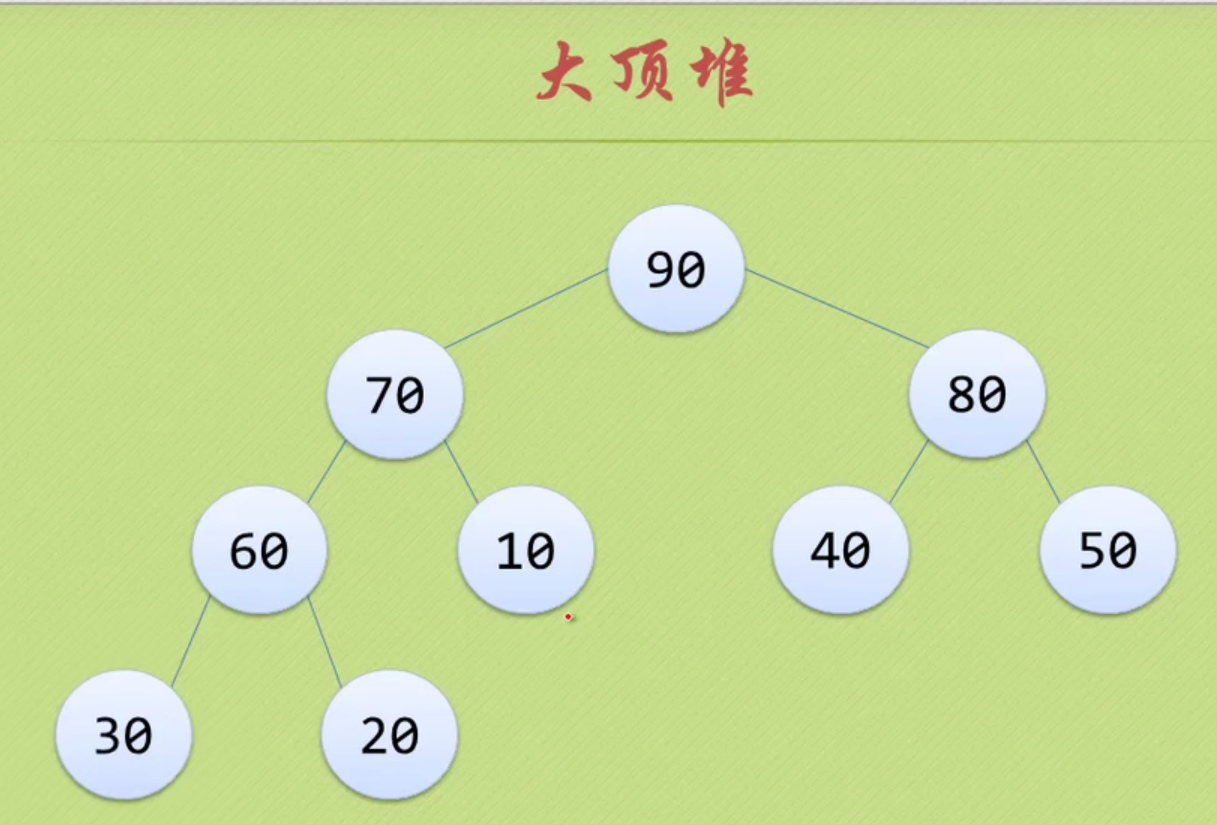
The above figure is a complete binary tree
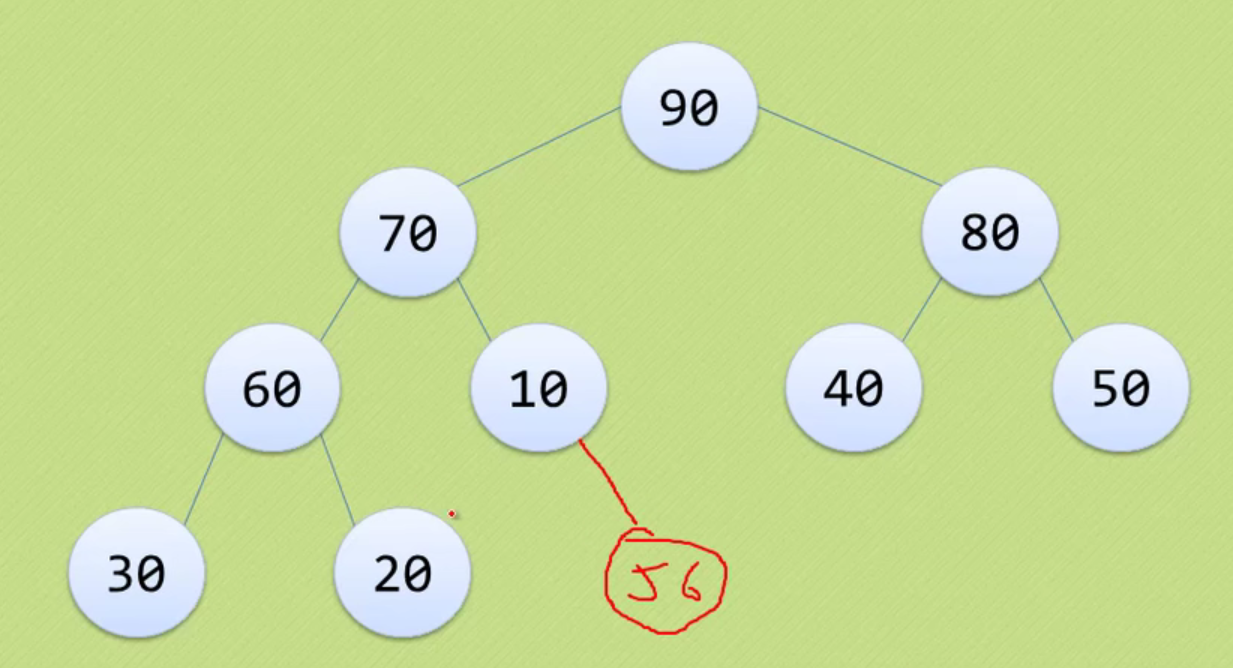
The figure above is not a complete binary tree
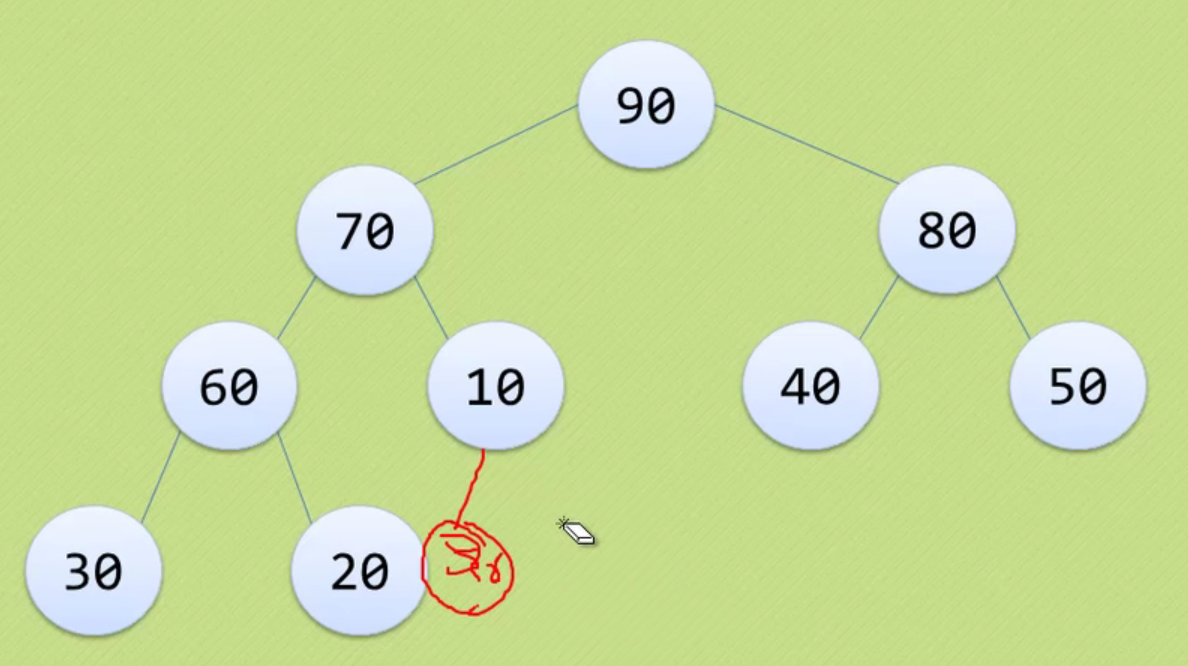
The above figure is a complete binary tree
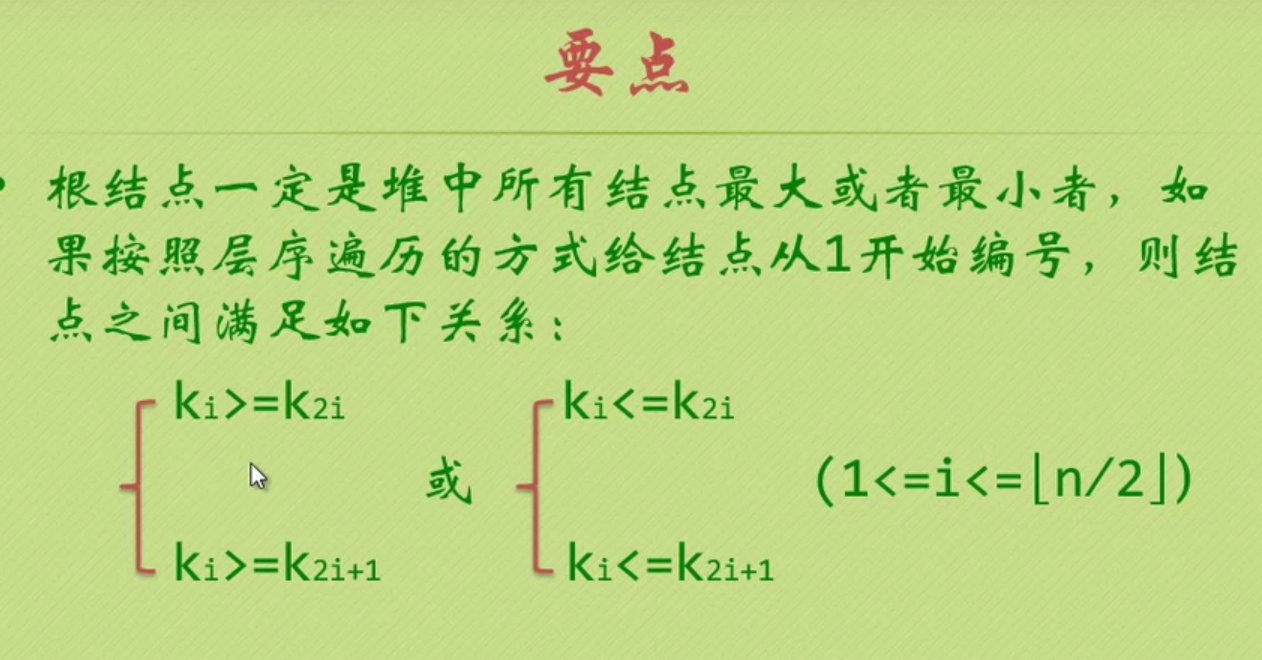
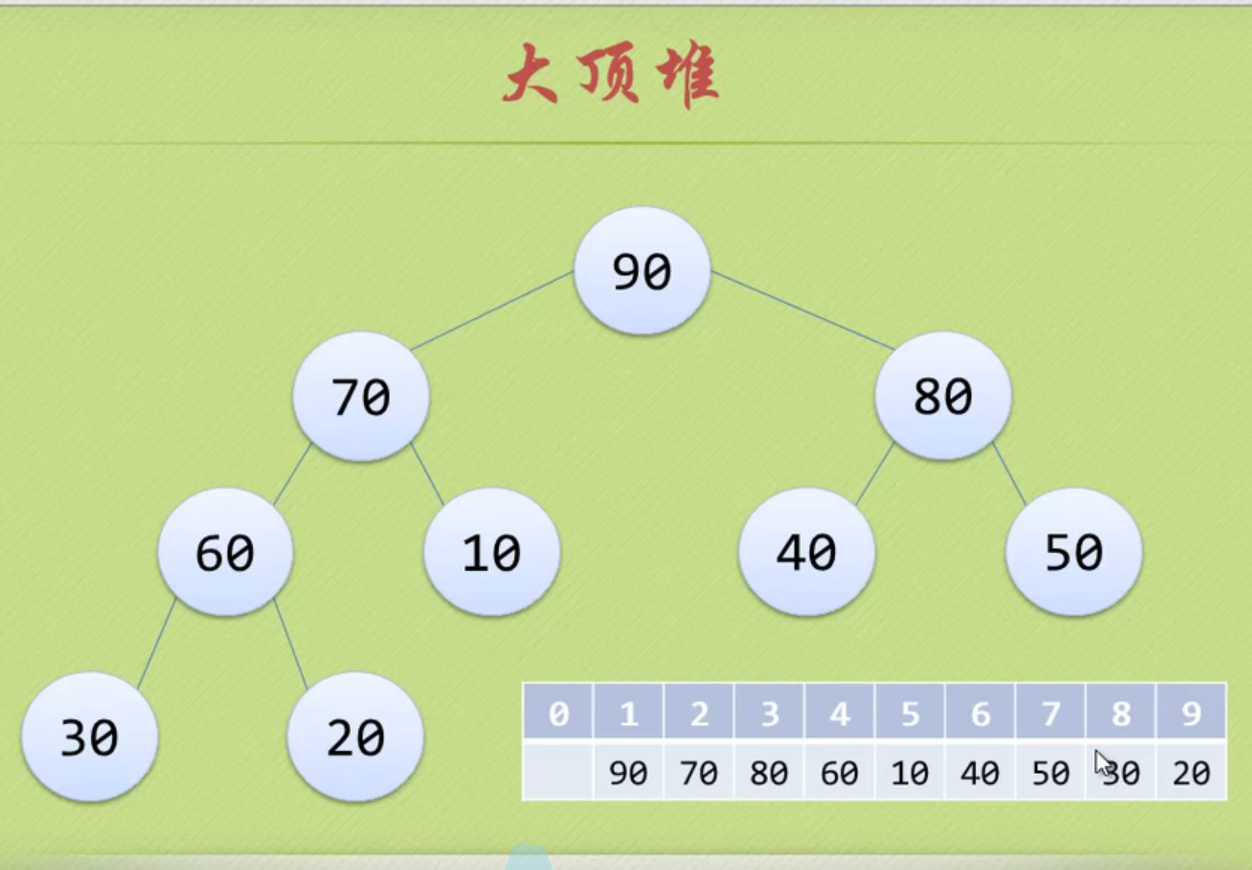
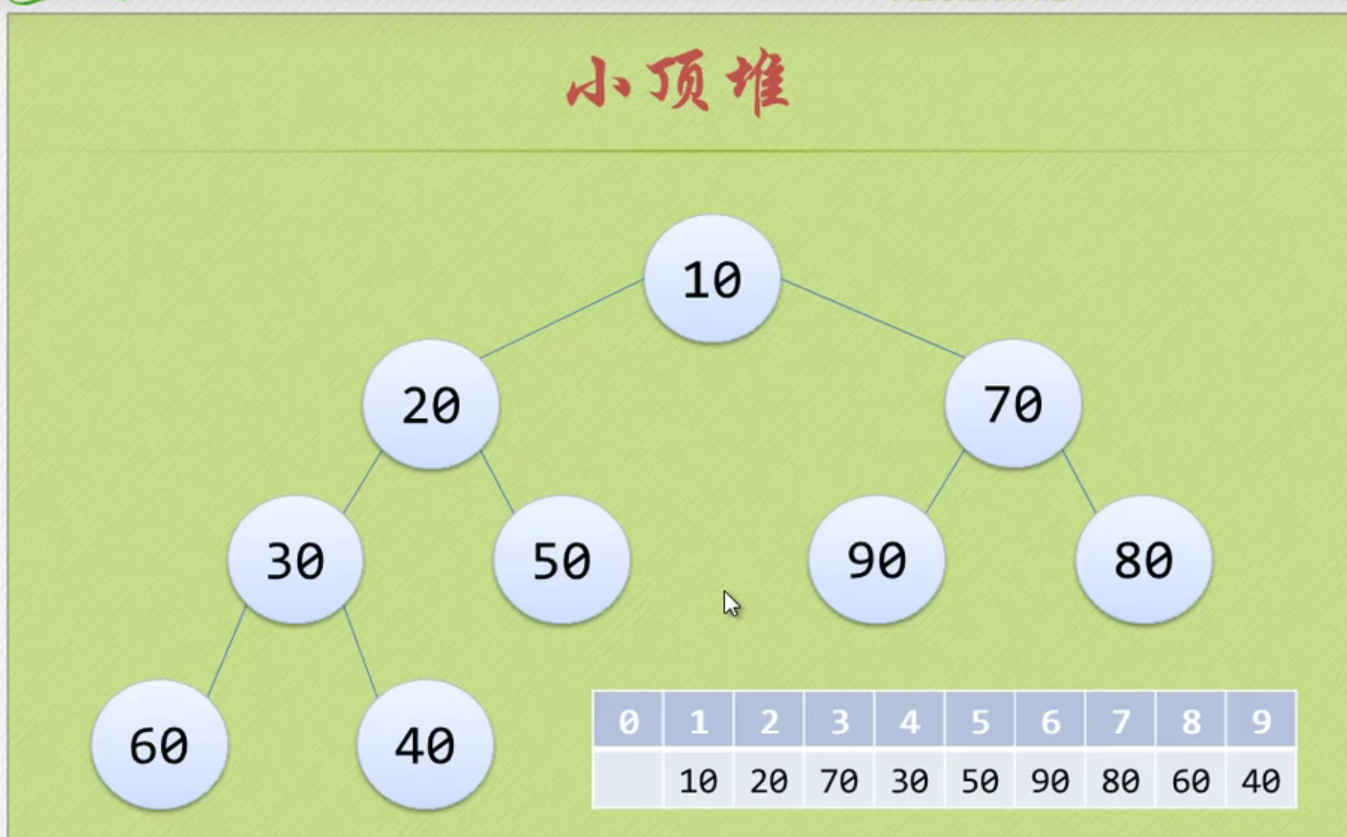
[external chain picture transferring... (i)