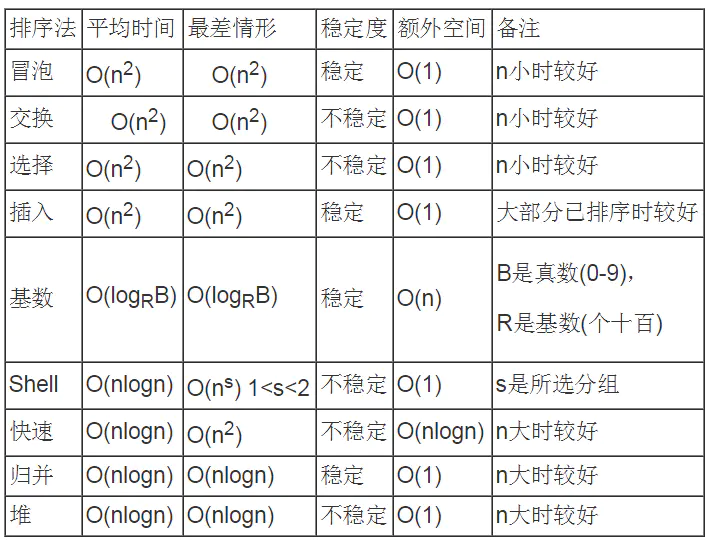
A summary table of all internal sorting algorithms
asadsa.png
Simple selection sorting
First find the smallest (large) element in the unsorted sequence, store it at the beginning of the sorted sequence, then continue to find the smallest (large) element from the remaining unsorted elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
Worst: O(n2)
Optimal: O(n2)
Average: O(n2)
public void selectSort(int[] a){
for(int i=0;i<a.length-1;i++){
int min=i;//Location of the smallest element
for(int j=i+1;j<a.length;j++){
if(a[j]<a[min]) min=j;
}
{int temp=a[min];a[min]=a[i];a[i]=temp;}//Exchange elements, put the smallest element in the head
}
}
Bubble sorting
The operation of bubble sorting algorithm is as follows:
- Compare adjacent elements. If the first is bigger than the second, exchange them.
- Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. When this is done, the last element will be the maximum number.
- Repeat the above steps for all elements except the last one.
- Continue to repeat the above steps every time for fewer and fewer elements, until no one pair of numbers needs to be compared.
Worst: O(n2)
Optimal: O(n)
Average: O(n2)
public static void bubbleSort(int[] a){
for(int i=0;i<a.length-1;i++){
for(int j=0;j<a.length-i-1;j++){
if(a[j]>a[j+1]) {int temp=a[j];a[j]=a[j+1];a[j+1]=temp;}//The exchange element position ensures that the large one is behind
}
}
}
Insert sort
Generally speaking, insertion sorting is implemented on array by in place. The specific algorithm is described as follows:
- Starting with the first element, the element can be considered sorted
- Take out the next element and scan from back to front in the sorted element sequence
- If the element (sorted) is larger than the new element, move it to the next location
- Repeat step 3 until you find a position where the sorted element is less than or equal to the new element
- After inserting a new element into the location
- Repeat steps 2-5
Worst: O(n2)
Optimal: O(n)
Average: O(n2)
Direct insert sort:
public static void insertSort(int[] a){
for(int i=1;i<a.length;i++){
for(int j=0;j<=i;j++){
if(a[j]>=a[i]){//Found the first element larger than yourself, inserted before the element
int temp=a[i];
for(int k=i-1;k>=j;k--) a[k+1]=a[k];//Move each element back one grid
a[j]=temp;
break;
}
}
}
}
Half insert sorting: it is to search for the first element larger than yourself and optimize it with half search:
public static void halfInsertSort(int[] a){
for(int i=1;i<a.length;i++){
int low=0;
int high=i;
while(low<=high){
int half=(low+high)/2;
if(a[half]<a[i]){//Insertion point in the high half
low=half+1;
}else{//Insertion point in lower half
high=half-1;
}
}
//The element pointed to by low or high is the first element larger than itself inserted before
int temp=a[i];
for(int k=i-1;k>=low;k--) a[k+1]=a[k];//Move each element back one grid
a[low]=temp;
}
}
Quick sort
Fast sorting uses the divide and conquer strategy to divide a list into two sub lists.
The steps are:
- To pick out an element from a sequence is called a pivot
- Reorder the sequence, place all elements smaller than the benchmark value in front of the benchmark, and place all elements larger than the benchmark value behind the benchmark (the same number can be on either side). At the end of the partition, the datum is in the middle of the sequence. This is called a partition operation.
- Recursively sorts the subsequences of the elements less than the reference value and the subsequences of the elements greater than the reference value.
Worst: O(n2)
Optimal: O(n log n)
Average: O(n log n)
//Here, left takes 0,right takes a.length-1
public static void quickSort(int[] a,int left,int right){
if(left<right){//Recursive exit condition
int i=left;//Left pointer
int j=right;//Right pointer
int x=a[left];//Select the first element as the ruler
while(i<j){
while(i<j && a[j]>=x) j--;//Find the first number less than x from right to left
if(i<j) a[i++]=a[j];
while(i<j && a[i]<x) i++;//Find the first number greater than or equal to x from left to right
if(i<j) a[j--]=a[i];
}
a[i]=x;//Insert ruler
quickSort(a,left,i-1);//Recursive left
quickSort(a, i+1, right);//Recursive right
}
}
At present, it's not good to select the first element as the scale. A safe way is to select with notes, but it's not good either. We usually use the median of three elements on the left, right and center as the scale to sort
public static void quickSortS(int[] a,int left,int right){
if(left<right){//Recursive exit condition
int i=left;//Left pointer
int j=right;//Right pointer
int center=(left+right)/2;
//Selecting scale by three number median Division
if((a[left]<=a[center]&&a[center]<=a[right])||(a[right]<=a[center]&&a[center]<=a[left])){
int tmp=a[left];
a[left]=a[center];
a[center]=tmp;//Remember to exchange
}else if((a[left]<=a[right]&&a[right]<=a[center])||(a[center]<=a[right]&&a[right]<=a[left])){
int tmp=a[left];
a[left]=a[right];
a[right]=tmp;
}
int x=a[left];//Ruler
while(i<j){
while(i<j && a[j]>=x) j--;//Find the first number less than x from right to left
if(i<j) a[i++]=a[j];
while(i<j && a[i]<x) i++;//Find the first number greater than or equal to x from left to right
if(i<j) a[j--]=a[i];
}
a[i]=x;//Insert ruler
quickSortS(a,left,i-1);//Recursive left
quickSortS(a, i+1, right);//Recursive right
}
}
Shell Sort
Hill sort, also known as descending incremental sort algorithm, is a more efficient version of insertion sort. Hill sort is an unstable sort algorithm.
Group according to the step size, and insert and sort each group
Worst: O (best n log2 n due to different steps)
Optimal: O(n)
Average: O (due to different steps)
public static void shellSort(int[] a){
int igap=a.length;//Initialization step, the first step is half of the array length
for(int gap=igap/2;gap>0;gap/=2){//step
for(int i=0;i<gap;i++){//Total step times insertion sorting
for(int j=i+gap;j<a.length;j+=gap){//Direct insertion sorting algorithm
for(int k=i;k<=j;k++){
if(a[k]>=a[j]){//Found the first element larger than yourself, inserted before the element
int temp=a[j];
for(int p=j-1;p>=k;p--) a[p+1]=a[p];//Move each element back one grid
a[k]=temp;
break;
}
}
}
}
}
}
Merge sort
The principle is as follows (assuming that the sequence has n elements in total):
- Merge two adjacent numbers to form floor(n/2) sequences. After sorting, each sequence contains two elements
- The above sequences are combined again to form floor(n/4) sequences, each of which contains four elements
- Repeat step 2 until all elements are sorted
Worst: O(n logn)
Optimal: O(n)
Average: O(n log n)
public static void mergeSort(int[] a,int first,int last){
if(first<last){
int[] temp=new int[a.length];
int middle=(first+last)/2;
mergeSort(a, first, middle);//Recursive left
mergeSort(a, middle+1, last);//Recursive right
//Merge two ordered sequences
int i=first;
int j=middle+1;
int k=0;
while(i<=middle&&j<=last){
if(a[i]<=a[j]){
temp[k++]=a[i++];
}else{
temp[k++]=a[j++];
}
}
while(i<=middle){
temp[k++]=a[i++];
}
while(j<=last){
temp[k++]=a[j++];
}
//Reassign the arranged temp to a
for(i=0;i<k;i++){
a[first+i]=temp[i];
}
}
}
Tree Selection Sort
Tree Selection Sort, also known as Tournament Sort, is a method of selecting and sorting according to the idea of tournament.
First, compare the keywords of n records in pairs, and then compare them between the smaller ones of [n/2] (round up). Repeat until the record with the smallest keyword is selected.
This process can be represented by a complete binary tree with n leaf nodes. Each non terminal node is the smaller value of left and right children, so that the root node is the minimum value of all leaf nodes. After outputting this value, change the minimum value of the leaf node to "maximum value", and then start from the leaf node, and compare it with its left and right brothers, Modify the value of each node in the path from the leaf node to the root node, then the value of the root node is the next smallest value. Similarly, all values can be discharged from the smallest to the largest
Although trees are usually implemented by arrays, the left child node of parent node I is in position (2i+1); the right child node of parent node I is in position (2i+2); the parent node of child node I is in position floor((i-1)/2)
Time complexity is O(n log n)
The disadvantage is that there is too much secondary storage space and redundant comparison with "maximum"
public static int[] TreeSelectSort(int[] data){
int dlong=data.length;
int tlong=2*dlong-1;
int low=0;
int[] tree=new int[tlong];
int[] ndata=new int[dlong];
for(int i=0;i<dlong;i++){
tree[tlong-i-1]=data[i];
}
for(int i=tlong-1;i>0;i-=2){
tree[(i-1)/2]=(tree[i]<tree[i-1]?tree[i]:tree[i-1]);
}
int minIndex;
while(low<dlong){
int min=tree[0];
ndata[low++]=min;
minIndex=tlong-1;
//Minimum found
while(tree[minIndex]!=min){
minIndex--;
}
tree[minIndex]=Integer.MAX_VALUE;
//Find its brother node
while(minIndex>0){//With parent node
if(minIndex%2==0){//Is the right node
tree[(minIndex-1)/2]=(tree[minIndex]<tree[minIndex-1]?tree[minIndex]:tree[minIndex-1]);
minIndex=(minIndex-1)/2;
}else{//Is the left node
tree[minIndex/2]=(tree[minIndex]<tree[minIndex+1]?tree[minIndex]:tree[minIndex+1]);
minIndex=minIndex/2;
}
}
}
return ndata;
}
Heap sort
Heap sorting is an optimization of tree selection and sorting, which is based on the data structure of "binary heap". Binary heap belongs to a complete binary tree. In addition, all the parent nodes should be larger or smaller than the left and right subtrees
If the parent node is larger than the left and right children, it is called the maximum binary heap, and if the parent node is smaller than the left and right children, it is called the minimum binary heap
Sorting based on the maximum binary heap is to construct a maximum heap first, then take out the root node, then build the remaining array elements into a maximum binary heap, and then take out the root node, so as to cycle until all elements are taken out
Like tree selection sorting, it is also implemented by array, refer to the previous section
At worst, the optimal and average time complexity are nlogn
public static void heapSort(int[] a){
//Build maximum heap
int size=a.length;
for(int i=(size-1-1)/2;i>=0;i--){
maxHeap(i,a,size);
}
for(int i=a.length-1;i>0;i--){
//The maximum value on the root node is continuously exchanged with the last one, and the last one is filtered out, pointing to the last pointer to move forward
int temp=a[i];
a[i]=a[0];
a[0]=temp;
size--;
//Ensure the maximum characteristics of the root node. All other nodes have been maintained
maxHeap(0, a,size);
}
}
//Keep maximum heap properties
private static void maxHeap(int i,int[] a,int size) {
int left=2*i+1;
int right=2*i+2;
int largest=i;
//Compare with left and right subtrees respectively, take the maximum value
if(left<=size-1&&a[left]>a[i]){
largest=left;
}
if(right<=size-1&&a[right]>a[largest]){
largest=right;
}
if(largest!=i){
//Swap root and maximum
int temp=a[i];
a[i]=a[largest];
a[largest]=temp;
//recursion
maxHeap(largest, a,size);
}
}
Bucket sort
The principle of bucket sort is very simple. It divides the array into a limited number of buckets.
Suppose there are N integers in array a to be sorted, and the range of data in array A is known [0, MAX]. During bucket sorting, create bucket array r with MAX capacity and initialize bucket array elements to 0; treat each cell in bucket array with MAX capacity as a "bucket".
In sorting, array A is traversed one by one, and the value of array A is used as the subscript of bucket array r. When the data in a is read, the value of the bucket is increased by 1. For example, if the array a[3]=5 is read, the value of r[5] will be + 1.
The time complexity of bucket sorting is O (n + k), and K is the range of value. In special cases, the lower bound of sorting is provided
public static void bucketSort(int[] a,int max){
int[] buckets;
if(a==null||max<1){
return;
}
buckets=new int[max];//Create an array with max capacity and initialize its data to 0
//count
for(int i=0;i<a.length;i++){
buckets[a[i]]++;
}
//sort
for(int i=0,j=0;i<max;i++){
while((buckets[i]--)>0){
a[j++]=i;
}
}
buckets=null;
}
Cardinality sort (multi key sort)
Cardinality sorting is no longer a conventional sorting method, it is more like the application of a sort method. Cardinality sorting must depend on another sort method. The general idea of Radix sorting is to divide the data to be sorted into multiple keywords for sorting, that is to say, the essence of Radix sorting is multi keyword sorting.
There are two solutions for multi key sorting:
Most significant digit first
Least significant digit first
Here we use LSD to sort keywords in buckets, which in essence becomes multiple bucket sorting
Time complexity is O(d(n+k),d is the number of keywords, and K is the value range
The number is within four digits, so the four keywords are tens of thousands of values
//Suppose that there are four keywords, one hundred thousand, for comparison within four digits. The same keyword is sorted by bucket
public static void radixSort(int[] a,int max,int d){
int rate=1;//Indicates key level
int[] buckets=new int[max];//Store single digit, tens digit, hundreds digit
List<Integer>[] temp=new List[max];//Store cached numbers
for(int i=0;i<d;i++){
//Clear operation
Arrays.fill(buckets, 0);
Arrays.fill(temp, null);
//Calculate the subkey of each data to be sorted
for(int j=0;j<a.length;j++){
int subKey=(a[j]/rate)%max;//Get one digit, ten digit, hundred digit
if(temp[subKey]==null) temp[subKey]=new ArrayList<Integer>();//Using list array to store cached numbers
temp[subKey].add(a[j]);
buckets[subKey]++;//Count + 1
}
//To sort is to take
for(int j=0,k=0;j<max;j++){
int t=0;
while((buckets[j]--)>0){
a[k++]=temp[j].get(t);
t++;
}
}
rate*=max;
}
}
Because array operation is more troublesome, if you have to store through array, you can only store the number of times, but not the whole number. When you take it out, I didn't think of a good way to restore it to a number. So I took a very stupid method, and then a cache list number group to store the number
Of course, it's a waste of space and trouble. It's a lot easier to use the linked list directly
public static void linkedRadixSort(int[] a,int max,int d){
ArrayList<ArrayList> list=new ArrayList<ArrayList>();
int rate=1;
for(int i=0;i<d;i++){
list.clear();
for(int j=0;j<max;j++){
list.add(new ArrayList<Integer>());
}
for(int j=0;j<a.length;j++){
int num=a[j];
int subKey=(num/rate)%max;
list.get(subKey).add(num);
}
for(int j=0,k=0;j<max;j++){
while(list.get(j).size()>0 && list.get(j)!=null){
a[k]=(Integer) list.get(j).remove(0);
k++;
}
}
rate*=max;
}
}
Although it's linked list, it's still put in array when it's collected, and there's still a lot of space to open up. So we use linked cardinal sort
The so-called chain type is stored in a linked list. The tail pointer of the previous group points to the head pointer of the next group. In this way, the linked list is easy to do
public static void linkedRadixSortS(Integer[] a,int max,int d){
List<Integer> slist=new ArrayList<Integer>();
ArrayList<ArrayList> list=new ArrayList<ArrayList>();
int rate=1;
slist.addAll(Arrays.asList(a));
for(int i=0;i<d;i++){
list.clear();
for(int j=0;j<max;j++){
list.add(new ArrayList<Integer>());
}
while(slist.size()>0){
int num=slist.remove(0);
int subKey=(num/rate)%max;
list.get(subKey).add(num);
}
for(int j=0;j<max;j++){
slist.addAll(list.get(j));
}
rate*=max;
}
a=slist.toArray(a);
}
The above three are only spatial optimizations, which have no effect on time complexity
External sort
All previous sorting algorithms belong to internal sorting, which need to load input data into memory. However, in some applications, their input data is too large to be loaded into memory, so external sorting is needed
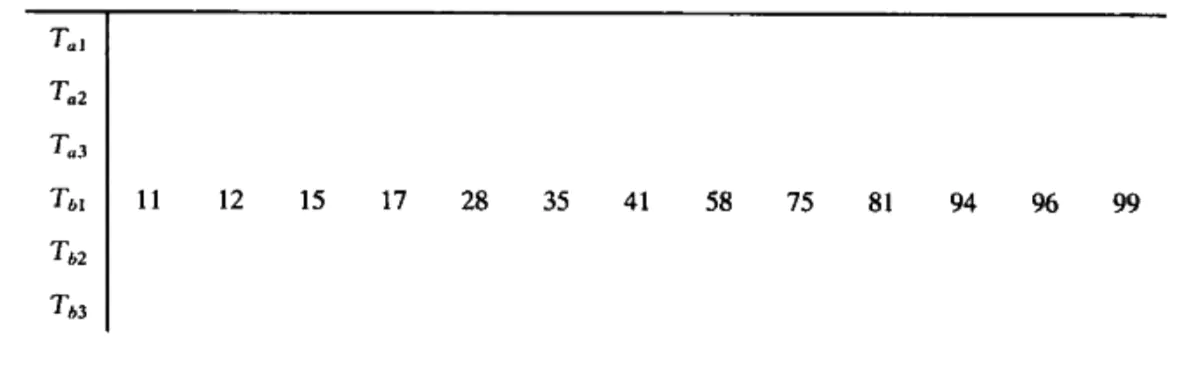
The basic external sorting algorithm uses merge sorting. There are four tapes, Ta1,Ta2,Tb1,Tb2, tape a and tape b, which can be used as input tape or output tape. M records are read from the input tape at a time (we take 3 records), and these records are sorted internally, and then alternately written to Tb1 or Tb2. Each group of sequenced records is called a sequence

1
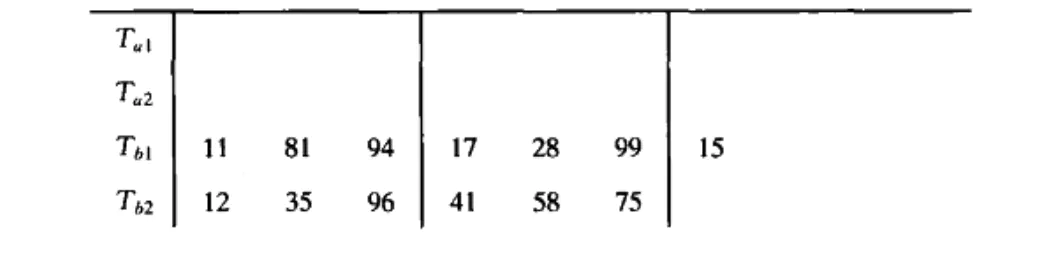
2
Now Tb1 and Tb2 both contain some sequential strings. We take out the first sequential string of each tape and merge them, and write the result to Ta1, which is a two times long sequential string. Then we take out the next sequential string from each tape, merge it and write it to Ta2. Continue this process until Tb1 or Tb2 is empty. Continue this process until a sequential string of N is obtained, This algorithm requires log(N/M) operations, as shown in the figure below
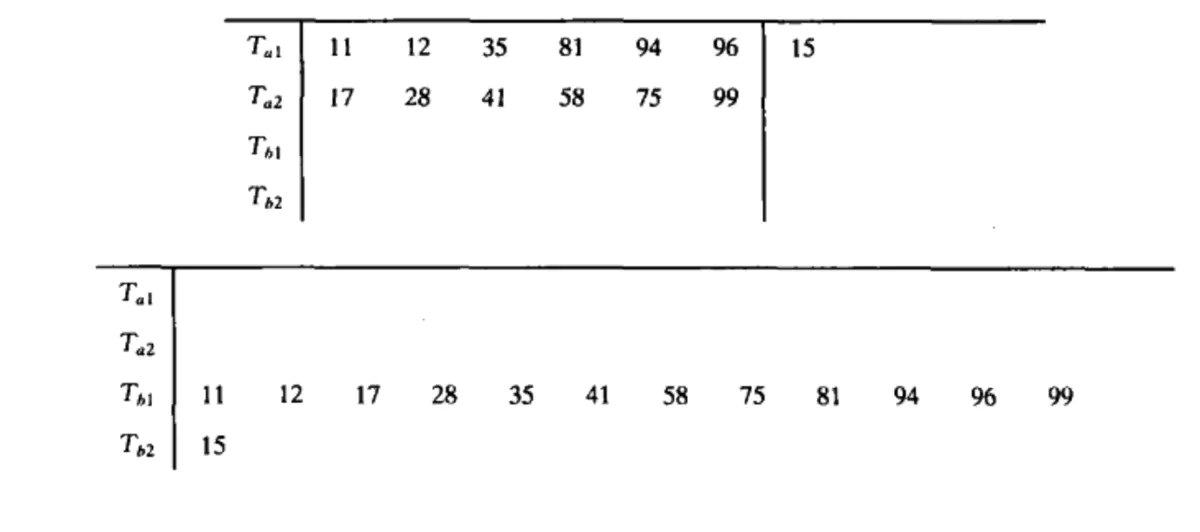
3

4
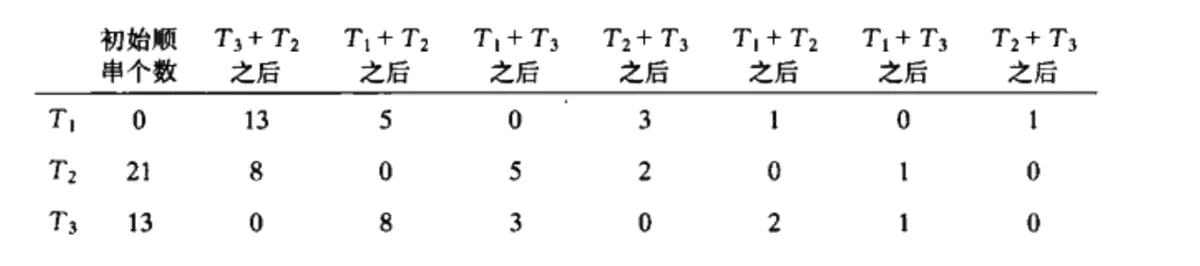
If we have additional tapes, we can reduce the number of times to sort the input data. We can do this by expanding the basic (2-way) merge to (k-way) merge. This is called multiplexing merge

5
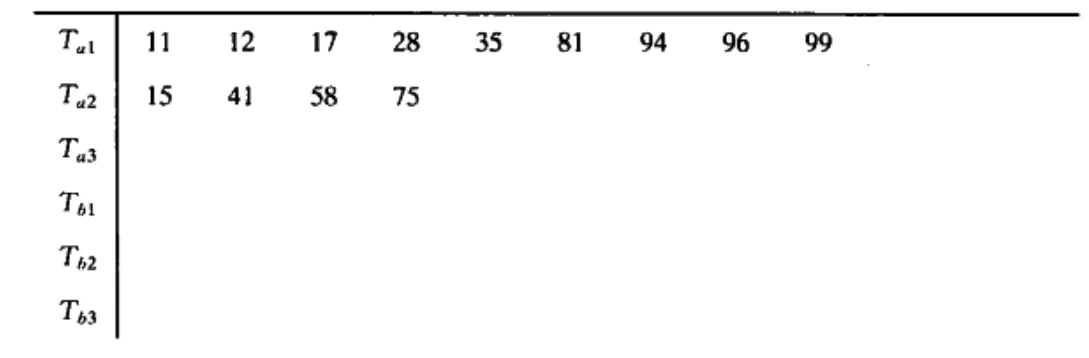
6
7
The k-path merging scheme discussed above requires 2k tapes. In fact, we can complete the sorting work by only using k+1 tapes, which is called multiphase merging. Take three tapes to complete the 2-path merging as an example:
8
Here the initial distribution of sequence is a key problem, in fact, the Fibonacci number is the best
For the construction of sequential strings, permutation selection and sorting can also be used
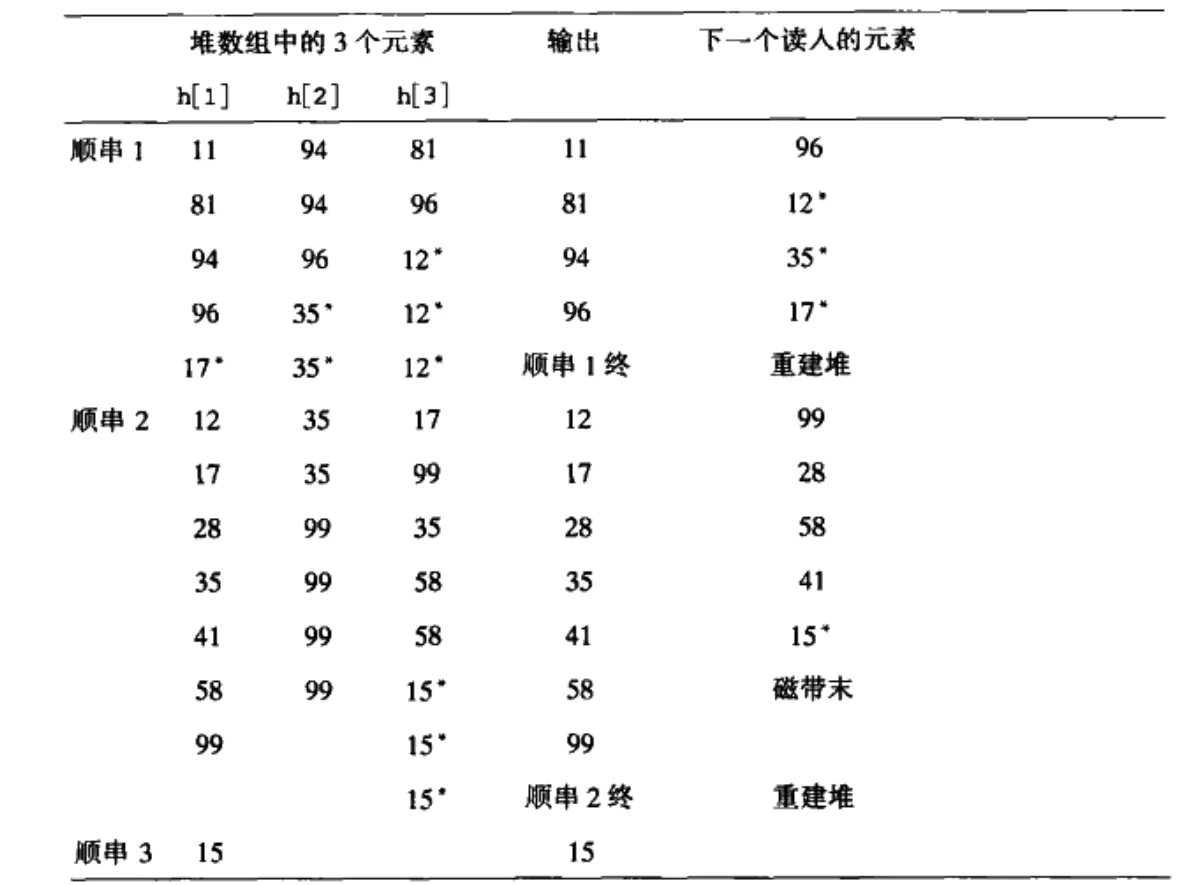
9
Next, complete external sorting
package com.fredal.structure;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Iterator;
import java.util.Random;
public class ExternalSort {
public static int BUFFER_SIZE = 10;
public File sort(File file) throws IOException {
ArrayList<File> files = split(file);
return process(files);
}
// recursive method to merge the lists until we are left with a
// single merged list
private File process(ArrayList<File> list) throws IOException {
if (list.size() == 1) {
return list.get(0);
}
ArrayList<File> inter = new ArrayList<File>();
for (Iterator<File> itr = list.iterator(); itr.hasNext();) {
File one = itr.next();
if (itr.hasNext()) {
File two = itr.next();
inter.add(merge(one, two));
} else {
return one;
}
}
return process(inter);
}
/**
* Splits the original file into a number of sub files.
*/
private ArrayList<File> split(File file) throws IOException {
ArrayList<File> files = new ArrayList<File>();
int[] buffer = new int[BUFFER_SIZE];
FileInputStream fr = new FileInputStream(file);
boolean fileComplete = false;
while (!fileComplete) {
int index = buffer.length;
for (int i = 0; i < buffer.length && !fileComplete; i++) {
buffer[i] = readInt(fr);
if (buffer[i] == -1) {
fileComplete = true;
index = i;
}
}
if (buffer[0] > -1) {
Arrays.sort(buffer, 0, index);
File f = new File("set" + new Random().nextInt());
FileOutputStream writer = new FileOutputStream(f);
for (int j = 0; j < index; j++) {
writeInt(buffer[j], writer);
}
writer.close();
files.add(f);
}
}
fr.close();
return files;
}
/**
* Merges two sorted files into a single file.
*
* @param one
* @param two
* @return
* @throws IOException
*/
private File merge(File one, File two) throws IOException {
FileInputStream fis1 = new FileInputStream(one);
FileInputStream fis2 = new FileInputStream(two);
File output = new File("merged" + new Random().nextInt());
FileOutputStream os = new FileOutputStream(output);
int a = readInt(fis1);
int b = readInt(fis2);
boolean finished = false;
while (!finished) {
if (a != -1 && b != -1) {
if (a < b) {
writeInt(a, os);
a = readInt(fis1);
} else {
writeInt(b, os);
b = readInt(fis2);
}
} else {
finished = true;
}
if (a == -1 && b != -1) {
writeInt(b, os);
b = readInt(fis2);
} else if (b == -1 && a != -1) {
writeInt(a, os);
a = readInt(fis1);
}
}
os.close();
return output;
}
private void writeInt(int value, FileOutputStream merged)
throws IOException {
merged.write(value);
merged.write(value >> 8);
merged.write(value >> 16);
merged.write(value >> 24);
merged.flush();
}
private int readInt(FileInputStream fis) throws IOException {
int buffer = fis.read();
if (buffer == -1) {
return -1;
}
buffer |= (fis.read() << 8);
buffer |= (fis.read() << 16);
buffer |= (fis.read() << 24);
return buffer;
}
/**
* @param args
* @throws IOException
*/
public static void main(String[] args) throws IOException {
File file = new File("mainset");
Random random = new Random(System.currentTimeMillis());
FileOutputStream fw = new FileOutputStream(file);
for (int i = 0; i < BUFFER_SIZE * 3; i++) {
int ger = random.nextInt();
ger = ger < 0 ? -ger : ger;
fw.write(ger);
fw.write(ger >> 8);
fw.write(ger >> 16);
fw.write(ger >> 24);
}
fw.close();
ExternalSort sort = new ExternalSort();
System.out.println("Original:");
dumpFile(sort, file);
File f = sort.sort(file);
System.out.println("Sorted:");
dumpFile(sort, f);
}
private static void dumpFile(ExternalSort sort, File f)
throws FileNotFoundException, IOException {
FileInputStream fis = new FileInputStream(f);
int i = sort.readInt(fis);
while (i != -1) {
System.out.println(Integer.toString(i));
i = sort.readInt(fis);
}
}
}
See extended reading for more articles and related downloads
By fredal
Link: https://www.jianshu.com/p/28d0f65aa6a1
Source: Jianshu
The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.