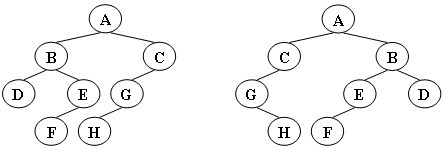
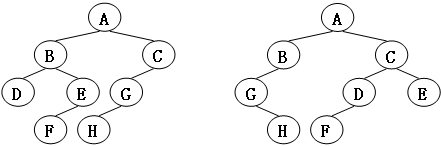
Give two trees T1 and T2. If T1 can be changed into T2 by several times, we call the two trees "isomorphic". For example, the two trees given in Figure 1 are isomorphic, because we exchange the left and right children of nodes A, B and G of one tree to get the other tree. Figure 2 is not isomorphic.

Now given two trees, please judge whether they are isomorphic.

Input format:

Input the information of 2 binary trees. For each tree, first give a nonnegative integer n in a row   (≤ 10), that is, the number of nodes of the tree (at this time, it is assumed that the nodes are numbered from 0 to n − 1); Then, line N and line I correspond to the i-th node, giving one English capital letter stored in the node, the number of its left child node and the number of its right child node. If the child node is empty, a "-" will be given at the corresponding position. The data given are separated by a space. Note: the title ensures that the letters stored in each node are different.

Output format:

If the two trees are isomorphic, output "Yes", otherwise output "No".

Input example 1 (corresponding to figure 1):

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

No blank lines at the end

Output example 1:

Yes

No blank lines at the end

Input example 2 (corresponding to figure 2):

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

Output example 2:

No

Program code:  

#include <iostream>
#define MaxSize 10
using namespace std;
typedef struct TreeNode{
	char data;
	int left;
	int right;
};
TreeNode T1[MaxSize], T2[MaxSize];
int CreatTree(TreeNode T[]);
int Isomorphic(int r1, int r2);//Judge whether isomorphism
int main()
{
	int r1,r2;
	r1 = CreatTree(T1);
	r2 = CreatTree(T2);
	if (Isomorphic(r1, r2))
		printf("Yes");
	else printf("No");
	return 0;
}

int CreatTree(TreeNode T[])
{
	int n;
	scanf("%d", &n);
	int i;
	int* check = new int[n];//Dynamically allocate arrays
	for (i = 0; i < n; i++)//Initialize the array = 0
	{
		check[i] = 0;
	}
	for (i = 0; i < n; i++)
	{
		char cl, cr;
		scanf("\n%c %c %c", &T[i].data, &cl, &cr);//Note that the input format should have spaces and enter!!!
		if (cl == '-')
		{
			T[i].left = -1;
		}
		else {
			T[i].left = cl - '0';
			check[T[i].left] = 1; //sign
		}
		if (cr == '-')
		{
			T[i].right = -1;
		}
		else {
			T[i].right = cr - '0';
			check[T[i].right] = 1; 
		}
	}
	int root = -1;
	for (i = 0; i < n; i++)
	{
		if (check[i] == 0) {
			root = i;
			break;
		}
	}
	delete[] check;
	return root;
}
int Isomorphic(int r1, int r2)
{
	//if (!r1 && !r2 ) return 1;//r1null r2null
	//if ((!r1 && r2)||(r1 && !r2)) return 0;//one of them is null
	//No! r1 is written in this way, because at first, if the coordinates of the incoming root node are 0, it is wrong

	if (r1 == -1 && r2 == -1)      //If both trees are empty, they are considered isomorphic 
		return 1;
	if ((r1 == -1 && r2 != -1) || (r1 != -1 && r2 == -1))    //If only one of the two trees is empty, it is considered that they are not isomorphic
		return 0;
	if (T1[r1].data != T2[r2].data)           //If the values of the root nodes of two trees are different, they are not isomorphic 
		return 0;
	if (T1[r1].left==-1 && T2[r2].left==-1)
		return Isomorphic(T1[r1].right, T2[r2].right);//If the left subtree is empty, pass it back to find the right subtree
	if ((T1[r1].left !=-1&& T2[r2].left!=-1) &&  ( T1[T1[r1].left].data == T2 [T2[r2].left].data)) {  //If the left subtree is not empty and the left subtree data is the same 
		return Isomorphic(T1[r1].left, T2[r2].left) && Isomorphic(T1[r1].right, T2[r2].right);//Then recursively enter the left and right subtrees to judge whether they are isomorphic 
	}
	else {  //If the two left subtrees are empty or the data of the two left subtrees are different, the left and right subtrees are exchanged to judge recursively 
		return Isomorphic(T1[r1].left, T2[r2].right) && Isomorphic(T1[r1].right, T2[r2].left);
	}
}

Summary:

          This problem has been done several times. The main idea is to find the left and right subtrees through a structural array and then use the input address. The second is the continuous recursion of judging isomorphism.

We need to pay more attention to several details.

First, scanf must be consistent with keyboard input, including spaces and carriage return (the carriage return usage when absorbing keyboard input is the same as getchar);

The second point is to be smart when isomorphism. If you want to make the code simpler, use it! r1 writes code from the perspective of judging that it is not empty rather than judging that it is equal to - 1. This is wrong, because if the root node coordinate is 0, the root node exists, but the program judges that the node does not exist, resulting in an error.