1. Tree structure

Trees are a special kind of data structure. Trees are called "trees" because they look like trees.But this tree draws a picture of a fallen tree with its roots on top and its leaves on the bottom.
A tree is a kind of graph. The difference between a tree and a graph is that a tree has no rings and a graph can have rings.

2. Why should we have a tree structure?

2.1 Tree structure is a natural structure

For example, a folder in a computer, we need to find a specific file, we need to go to a folder to find this file, the file storage structure of the computer comes from life.
For example, in a library, we know that there are historical, mathematical and computer classes in the library. If we want to find books about java, we need to go to Java for computer classes to find the books we need.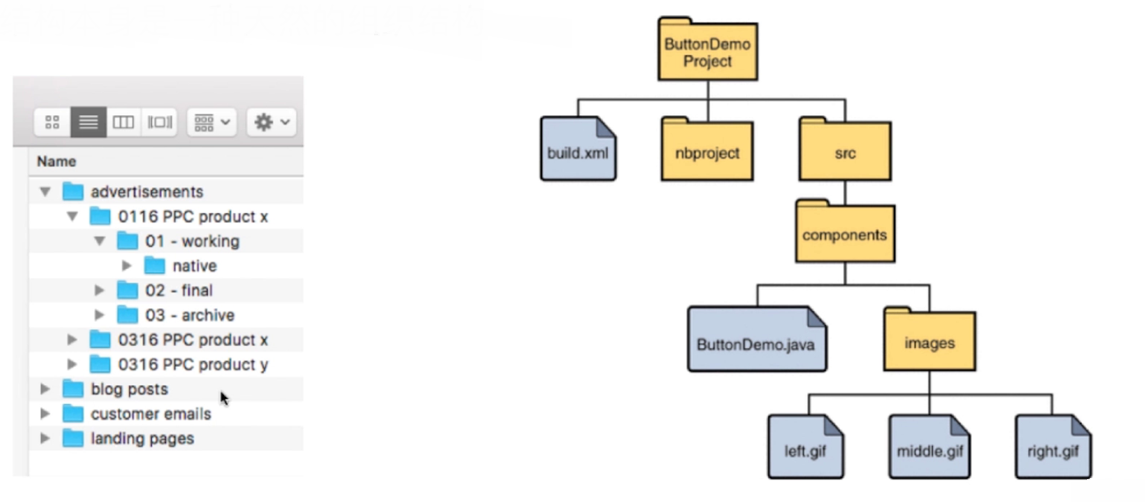

For example, the hierarchy structure within the company: CEO, HR CTO, and so on, as well as our more common family tree and so on, are similar to the tree structure

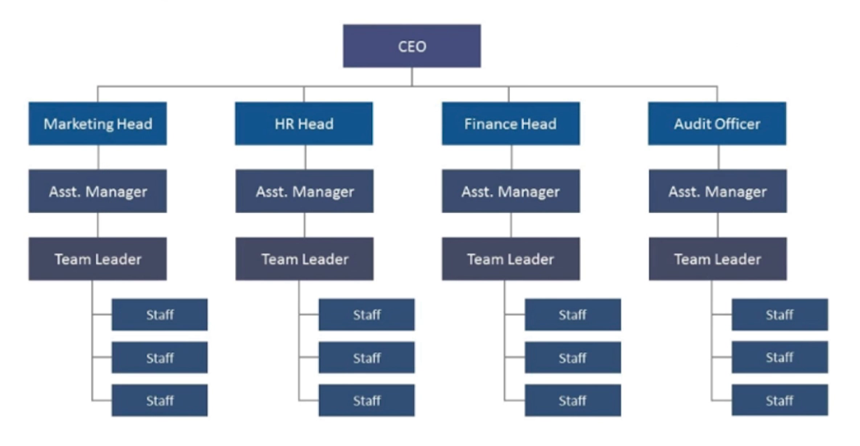
• Using tree structure for data is more efficient

3. Binary Search Tree

3.1 Features

• Binary search tree is a dynamic data structure
• A binary search tree is also a binary tree (also called a multifork tree)
• Each node of a binary search tree has a greater value than all nodes of its left subtree, and each node has a smaller value than all nodes of its right subtree
• Stored elements must be comparable, Java requires that the data type saved by the Binary Search Tree implement the Comparable interface or use an additional comparator
• Each subtree is also a binary search tree
• A binary search tree has a unique root node and its leaf node is at the bottom of the binary tree
  
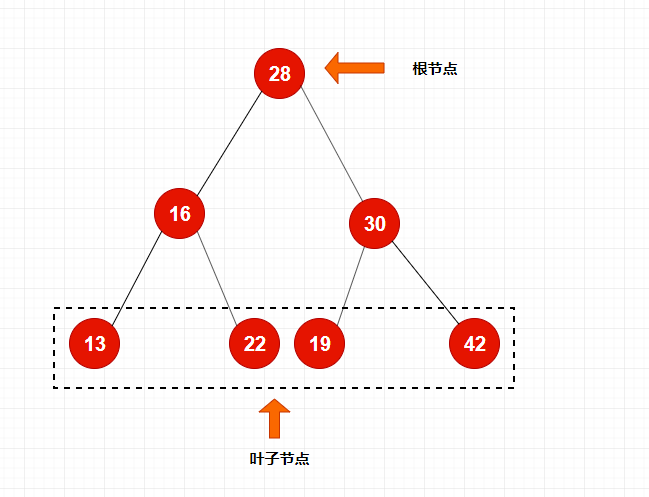
  The binary search tree has root-only nodes, each node has at most two children (left child on the left and right child on the right), and each node has at most one father.

The natural recursive nature of binary search trees

• The left subtree of each node is also a binary tree
• The right subtree of each node is also a binary tree
  

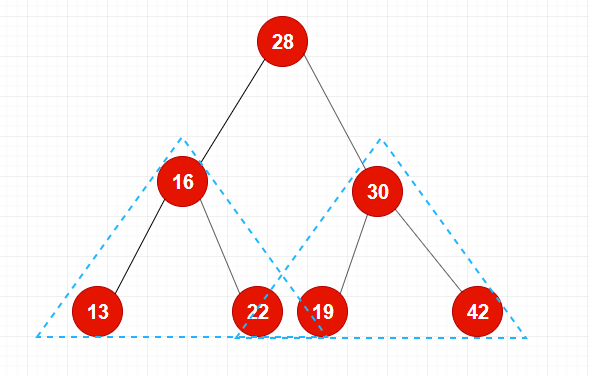
Binary tree is not necessarily full, a computer is also a binary tree, empty is also a binary tree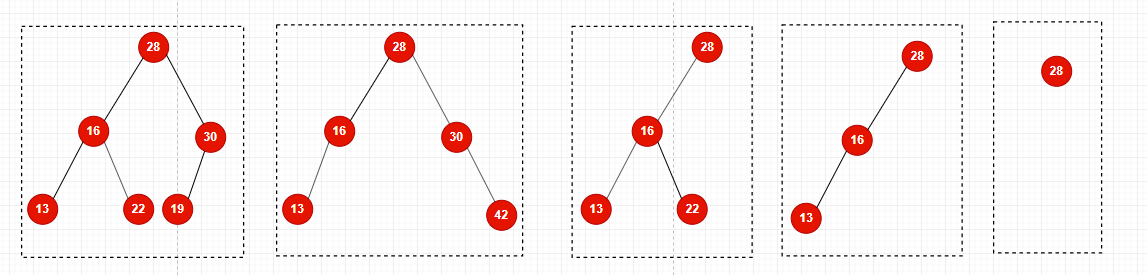

4. Specific Code Implementation

Before proceeding, define a node class that supports generics to store information about each node of the Binary Search Tree, which is an internal class of the Binary Search Tree. The class declarations of the Binary Search Tree and the Node Node Class are as follows:

public class BST<E extends Comparable<E>> {

    private class Node{
        public E e;
        public Node left,right;

        public Node(E e){
            this.e = e;
            left = null;
            right = null;
        }
    }
	//node
    private Node root;
    // Tree capacity
    private int size;

    public BST(){
        root = null;
        size  = 0;

    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

}

4.1 Add Elements

Binary search tree adds elements in a non-recursive way, much like a list of chains. Because of the recursive nature of the binary search tree itself, it is easy to use recursion to add elements to the binary search tree.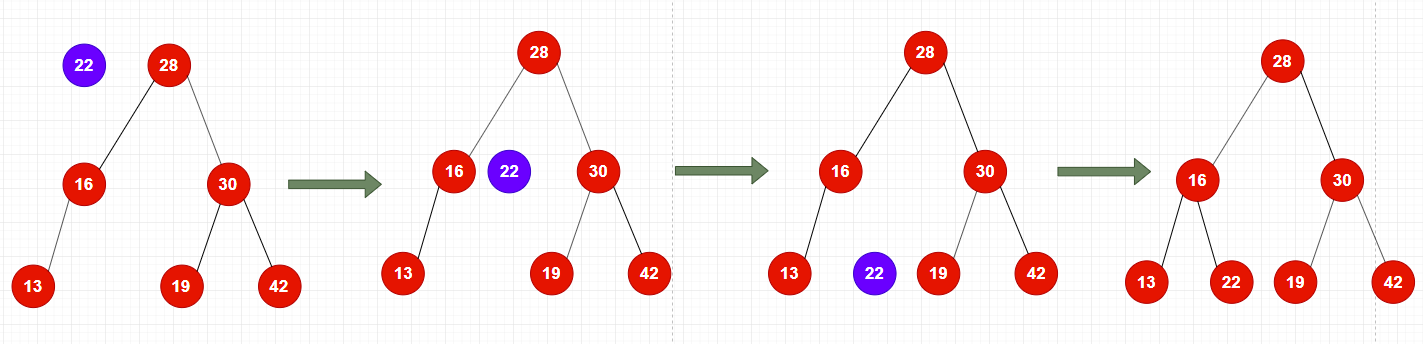

Code implementation:

 //Add a new element e to the binary search tree
    public void add(E e){
        root = add(root,e);
    }

    //Insert element E into a binary search tree rooted in Node, recursive algorithm
    //Returns the root of the binary search tree after inserting a new node
    private Node add(Node node,E e){

        if(node == null){
            size++;
            return new Node(e);
        }
        if(e.compareTo(node.e) < 0)
            node.left = add(node.left,e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right,e);

        return node;
    }

4.2 Find Elements

Since the Binary Search Tree has no subscripts, we need to define a contains() method for the Binary Search Tree search operation to see if the Binary Search Tree contains an element and return a Boolean variable

Code implementation:

    //See if dichotomy contains element e in the search tree
    public boolean contains(E e){
        return contains(root,e);
    }

    //Recursive algorithm to see if element e is included in a binary search tree rooted in Node
    private boolean contains(Node node,E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left,e);
        else //e.compareTo(node.e) > 0
            return contains(node.right,e);
    }

4.3 Traversal operation

1. What is traversal operation

• Traversal is to access all nodes once
• Reasons for access are business related
• Traversal Classification

    //Binary Search Tree Preorder Traversal
    public void preOrder(){
        preOrder(root);
    }

    //Pre-order traverses a binary search tree rooted in Node, recursive algorithm
    private void preOrder(Node node){

        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    public void preOrderNR(){
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);

            if(cur.left != null)
                stack.push(cur.left);
        }
    }

3. Intermediate traversal

    //Mid-order traversal of a binary search tree
    public void inOrder(){
        inOrder(root);
    }

    //A recursive algorithm for traversing a binary search tree rooted in Node in middle order
    private void inOrder(Node node){
        if(node ==null)
            return;
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

4. Post-order traversal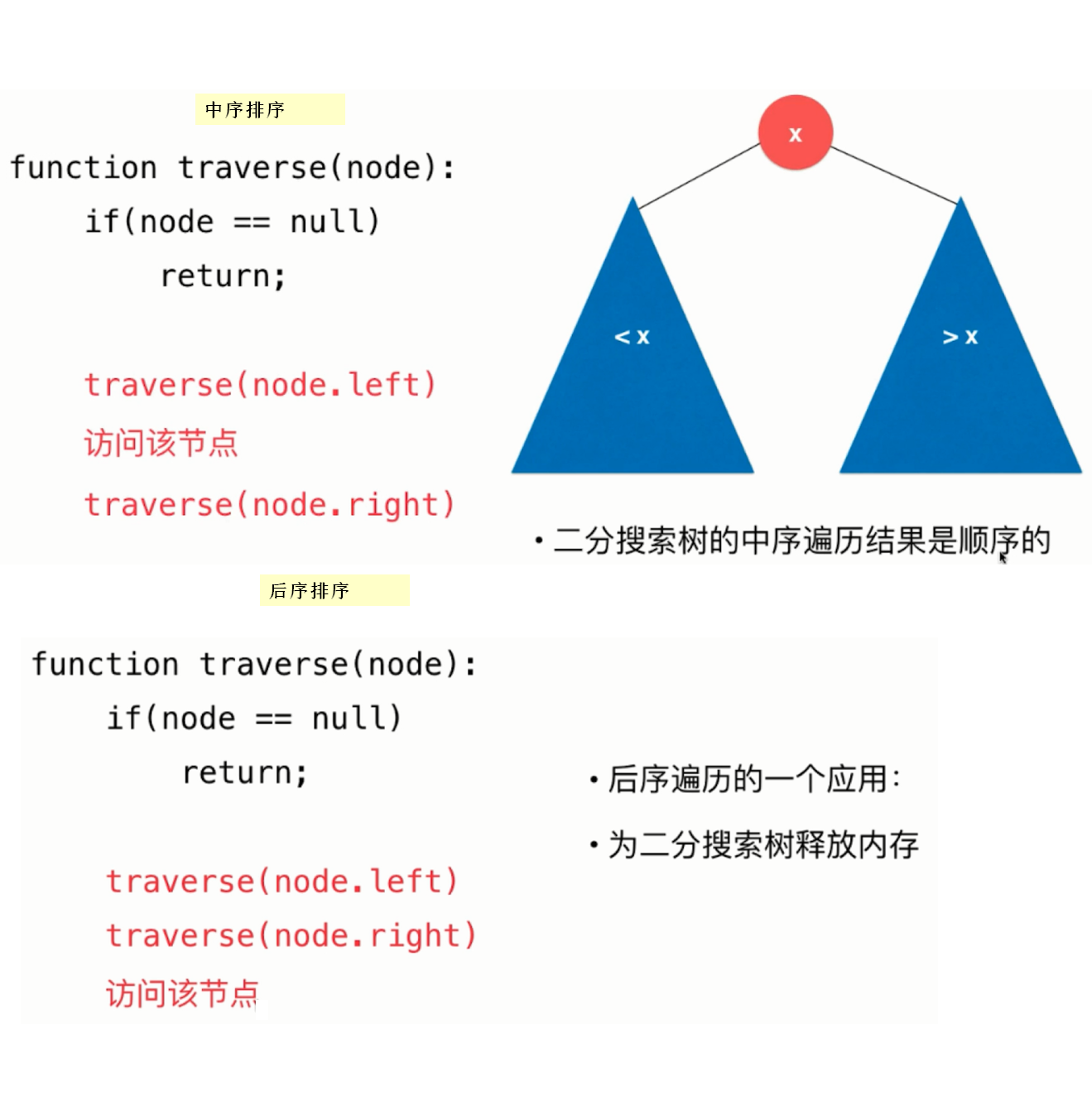

    //Post-Ordered Traversal of Binary Search Tree
    public void postOrder(){
        inOrder(root);
    }

    public void levelOrder(){
        Queue<Node> q = new LinkedList<Node>();
        q.add(root);

        while (!q.isEmpty()){
            Node cur = q.remove();
            System.out.println(cur.e);

            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);

        }
    }


    //A recursive algorithm for traversing a binary search tree rooted in Node
    private void postOrder(Node node){
        if(node ==null)
            return;
        inOrder(node.left);
        inOrder(node.right);
        System.out.println(node.e);
    }

5. Understanding before, during and after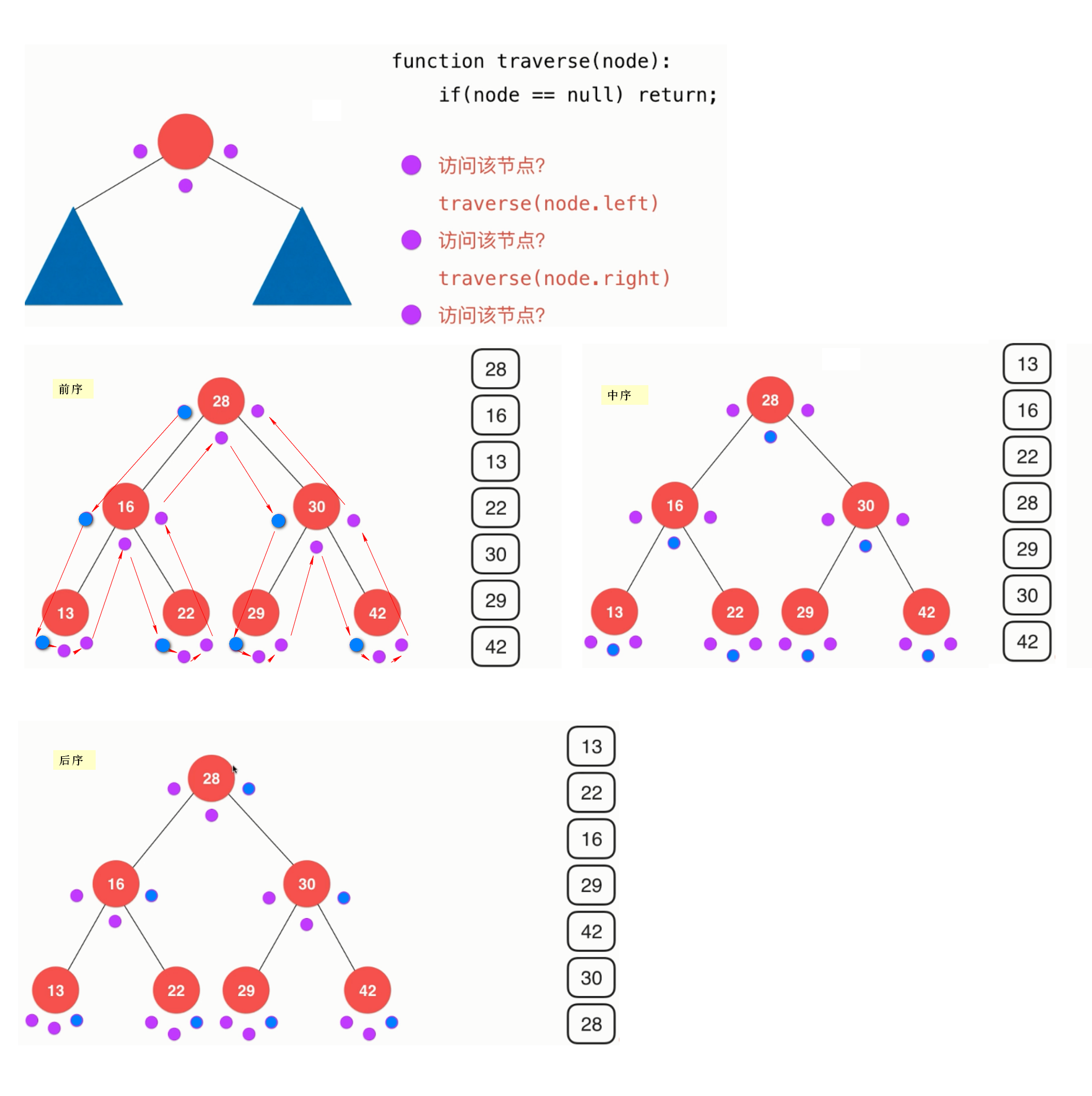

Binary Search Tree Preorder Non-Recursive Writing

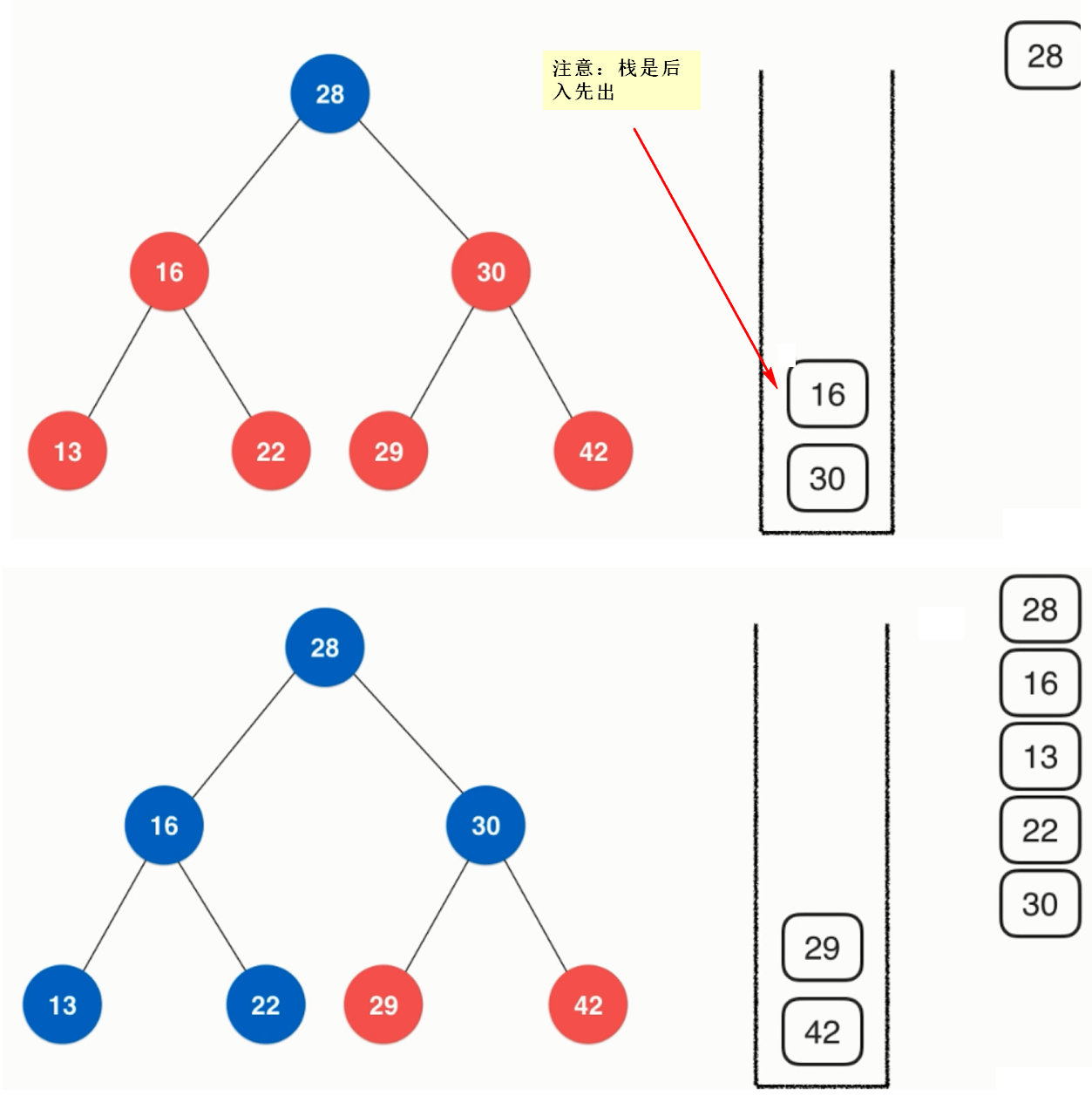
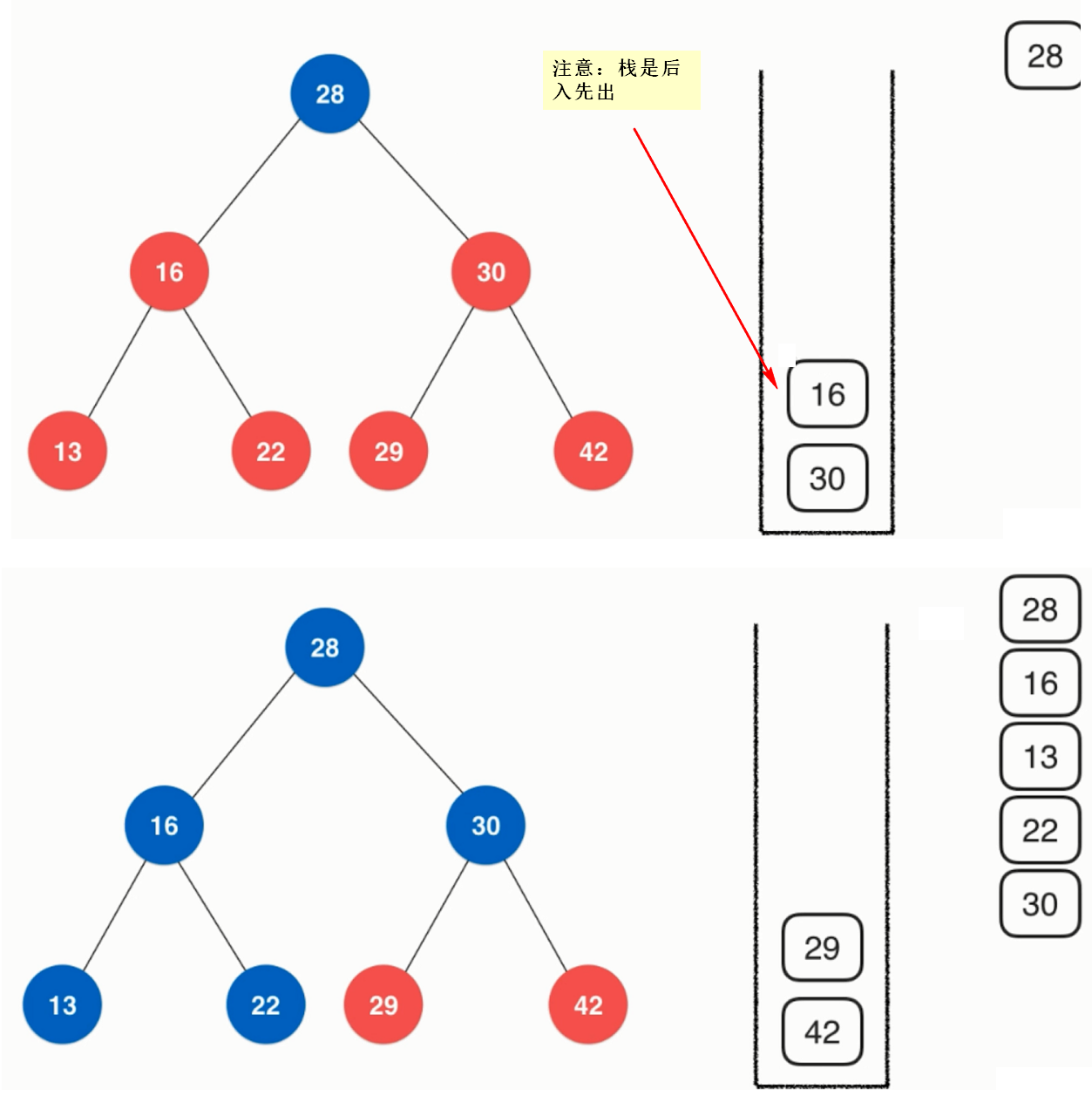
Not finished yet.