Heap (heap)

It is mentioned in linear structure queue that a queue is called Priority Queue. The priority of getting elements is based on the priority of elements, not the priority of elements entering the queue.

How to organize priority queues?

We use the complete binary tree to represent the priority queue. Any node is the maximum / minimum value of its subtree, which is called heap. The heap is divided into big top heap and small top heap. From the name, we can see that the top of the corresponding node of the big top pair is the maximum value, and the small top heap is the same.

Big top pile: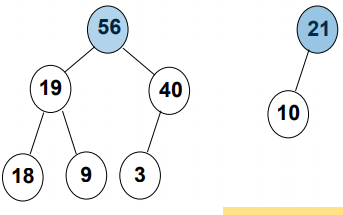

Small top pile: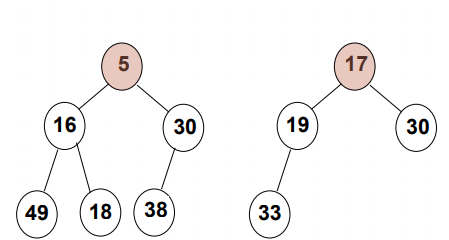

Two characteristics of heap

• Structure: a complete binary tree represented by an array
• Ordering: the key of any node is the maximum / minimum value of all nodes in its subtree
  

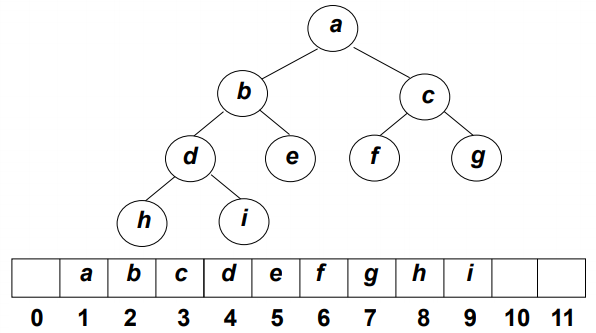
Abstract data type description of heap

Type name: maximum heap

Data object set: perfect binary tree, the element value of each node is not less than that of other child nodes

Operation set:

• maxheap create (int maxsize): creates an empty maximum heap.

• Boolean isfull (maxheap H): judge whether the maximum heap H is full.

• insert (maxheap h, ElementType item): insert the element item into the maximum heap H.

• Boolean isempty (maxheap H): judge whether the maximum heap H is empty.

• ElementType deletemax (maxheap h): returns the largest element in H (high priority).

Heap structure:

typedef struct heapsturct
{
	ElementType *Elements ;//Position 0 stores a sentinel with an infinite value. Easy to insert later
	int Size ;//Number of elements stored in the current heap
	int Capacity ;//Maximum number of piles
}*MaxHeap;

Create heap

MaxHeap Create( int MaxSize )//Create an empty maximum heap.
{
	MaxHeap H = (MaxHeap)malloc(sizeof(struct heapsturct));
	H->Elements = (ElementType *)malloc(sizeof (ElementType) * (MaxSize+1)); //Size of allocation array
	H->Capacity = MaxSize ; //Record memory size
	H->Size = 0 ;
	H->Elements[0] = Maxn ;//Sentinel establishment
	return H;
}

Heap insertion

1. First, put the newly added element at the end of the binary tree, that is, the last position of the array.
2. Then compare the size with the parent node of the new element location, and exchange if the size is large

i= ++H->Size ;
for (;item > H->Elements[i/2] ; i=i/2  ) // There's a big sentry at position 0. It's over at the top 
		H->Elements[i] = H->Elements[i/2];

i is the position of the inserted element at the beginning. This statement can make the node of the new element move down until i reaches the position where the parent node of the new element is larger than it. Here, the role of the sentry is that when the inserted element is the current largest element, when i reaches the position of 1 (tree root), it will be smaller than the Sentry (the sentry is set to be large), so the cycle will stop automatically Stop, this is the role of sentinels.

1. Find the right place to store the new elements

void Insert( MaxHeap H, ElementType item )//Insert element item into maximum heap H
{
	if (IsFull(H))
	{
		cout <<"Pile up"<<endl; 
		return ;
	}
	int i= ++H->Size;
	
	for (;item > H->Elements[i/2] ; i=i/2  ) // There's a big sentry at position 0. It's over at the top 
		H->Elements[i] = H->Elements[i/2];
	
	H->Elements[i] = item ;	
}

Heap delete maximum element

1. Save the maximum value first, and return at the end of the function
2. Put the last element at the root of the tree, that is, at the deletion position, and the heap length is reduced by one
3. Always select the maximum value of left and right child nodes to compare with the value put up. If it is larger than this value, then exchange the position until both left and right nodes are smaller than this element.

for (parent=1 ; parent*2<H->Size ;parent = child)
	{
		child = parent*2 ;
		if (child<H->Size && H->Elements[child]<H->Elements[child+1])//If child = = H - > size, there is no right node
			child ++ ;
		if (item > H->Elements[child]) break ;//parent position meets the conditions
		else 
		H->Elements[parent] = H->Elements[child]; //Change of position
	}

At the end of this cycle, the position of the parent is consistent with the position of the item element insertion

ElementType DeleteMax( MaxHeap H )//Returns the largest element in H (high priority)
{
	if (IsEmpty(H))
	{
		cout <<"The biggest pile is empty"<<endl;
		return H->Elements[0]; 
	}
	int item  = H->Elements[H->Size--];
	int value = H->Elements[1];
	int parent , child ;
	for (parent=1 ; parent*2<H->Size ;parent = child)
	{
		child = parent*2 ;
		if (child<H->Size && H->Elements[child]<H->Elements[child+1])
			child ++ ;
		if (item > H->Elements[child]) break ;
		else 
		H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = item ;
	return value ;
}

Test code:

#include <iostream>
#include <stdlib.h>
#define ElementType int 
#define Maxn  1<<30 
using namespace std ;

typedef struct heapsturct
{
	ElementType *Elements ;
	int Size ;
	int Capacity ;
}*MaxHeap;


MaxHeap Create( int MaxSize )//Create an empty maximum heap.
{
	MaxHeap H = (MaxHeap)malloc(sizeof(struct heapsturct));
	H->Elements = (ElementType *)malloc(sizeof (ElementType) * (MaxSize+1)); 
	H->Capacity = MaxSize ;
	H->Size = 0 ;
	H->Elements[0] = Maxn ;
	return H;
}

bool IsFull( MaxHeap H )//Determine whether the maximum heap H is full.
{
	if (H->Capacity <= H->Size)
		return true ;
	else 
		return false ;
}


void Insert( MaxHeap H, ElementType item )//Insert the element item into the maximum heap H.
{
	if (IsFull(H))
	{
		cout <<"Pile up"<<endl; 
		return ;
	}
	int i= ++H->Size;
	
	for (;item > H->Elements[i/2] ; i=i/2  ) // There's a big sentry at position 0. It's over at the top 
		H->Elements[i] = H->Elements[i/2];
	
	H->Elements[i] = item ;	
}
bool IsEmpty( MaxHeap H )//Determine whether the maximum heap H is empty.
{
	if (H->Size == 0)
		return true ;
	else 
		return false ;
}

ElementType DeleteMax( MaxHeap H )//Returns the largest element in H (high priority)
{
	if (IsEmpty(H))
	{
		cout <<"The biggest pile is empty"<<endl;
		return H->Elements[0]; 
	}
	int item  = H->Elements[H->Size--];
	int value = H->Elements[1];
	int parent , child ;
	for (parent=1 ; parent*2<H->Size ;parent = child)
	{
		child = parent*2 ;
		if (child<H->Size && H->Elements[child]<H->Elements[child+1])
			child ++ ;
		if (item > H->Elements[child]) break ;
		else 
		H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = item ;
	return value ;
}


int main ()
{
	MaxHeap H ;
	H = Create(10);
	cout <<"Insert element:";
	for (int i=0;i<11;i++) // Insert 11 elements the 11th element is full 
	{
		int item = rand();
		cout <<item <<" "; 
		Insert(H,item); 
	} 
	cout <<endl;
	for (int i=0;i<10;i++)
	cout <<DeleteMax(H)<<endl;
	cout <<DeleteMax(H)<<endl; //Empty space! 
}

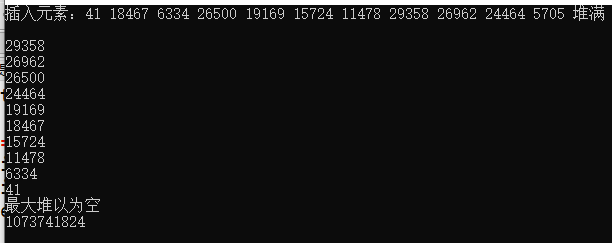
If one element is inserted into the established heap one by one according to the above method, the time complexity is O (nlogn)

A method of linear pile building

1. Store n elements in input order. Structure properties of complete binary trees satisfied first
2. Adjust the position of each node. To meet the ordered characteristics of the largest heap

The adjustment strategy starts from the parent node of the last node and ends at the root node 1, which is adjusted from the bottom element to the top

void PerDown(MaxHeap H , int p) // The method of adjusting the node position to p is similar to that of deleting the maximum value 
{
	int parent,child ;
	ElementType x;
	x = H->Elements[p];
	for (parent = p ; parent*2<=H->Size;parent = child)
	{
		 child = parent*2 ;
		 if (child <H->Size && H->Elements[child]<H->Elements[child+1])
		 	child ++;
		if (x > H->Elements[child]) break ;
		else 
			H->Elements[parent] = H->Elements[child];
	 } 
	 H->Elements[parent] = x ;
} 

Test code:

#include <iostream>
#include <stdlib.h>
#define ElementType int 
#define Maxn  1<<30 
using namespace std ;

typedef struct heapsturct
{
	ElementType *Elements ;
	int Size ;
	int Capacity ;
}*MaxHeap;


MaxHeap Create( int MaxSize )//Create an empty maximum heap.
{
	MaxHeap H = (MaxHeap)malloc(sizeof(struct heapsturct));
	H->Elements = (ElementType *)malloc(sizeof (ElementType) * (MaxSize+1)); 
	H->Capacity = MaxSize ;
	H->Size = 0 ;
	H->Elements[0] = Maxn ;
	return H;
}

bool IsFull( MaxHeap H )//Determine whether the maximum heap H is full.
{
	if (H->Capacity <= H->Size)
		return true ;
	else 
		return false ;
}

bool IsEmpty( MaxHeap H )//Determine whether the maximum heap H is empty.
{
	if (H->Size == 0)
		return true ;
	else 
		return false ;
}

ElementType DeleteMax( MaxHeap H )//Returns the largest element in H (high priority)
{
	if (IsEmpty(H))
	{
		cout <<"The biggest pile is empty"<<endl;
		return H->Elements[0]; 
	}
	int item  = H->Elements[H->Size--];
	int value = H->Elements[1];
	int parent , child ;
	for (parent=1 ; parent*2<H->Size ;parent = child)
	{
		child = parent*2 ;
		if (child<H->Size && H->Elements[child]<H->Elements[child+1])
			child ++ ;
		if (item > H->Elements[child]) break ;
		else 
		H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = item ;
	return value ;
}

void PerDown(MaxHeap H , int p) // The method of adjusting the node position to p is similar to that of deleting the maximum value 
{
	int parent,child ;
	ElementType x;
	x = H->Elements[p];
	for (parent = p ; parent*2<=H->Size;parent = child)
	{
		 child = parent*2 ;
		 if (child <H->Size && H->Elements[child]<H->Elements[child+1])
		 	child ++;
		if (x > H->Elements[child]) break ;
		else 
			H->Elements[parent] = H->Elements[child];
	 } 
	 H->Elements[parent] = x ;
} 


void BuildGeap(MaxHeap H)
{
	int i ;
	for (i = H->Size/2;i>0;i--)//Adjust one by one from the last parent node to the root node 1 
		PerDown(H,i);
}

int main ()
{
	MaxHeap H ;
	H = Create(10);
	cout <<"Insert element:";
	for (int i=0;i<10;i++)
	{
		int item = rand();
		cout <<item <<" "; 
		H->Elements[++H->Size] = item ;  //Put elements directly in order
	} 
	cout <<endl;
	BuildGeap(H); 
	for (int i=0;i<10;i++)
	cout <<DeleteMax(H)<<endl;
}

Huffman tree and Huffman coding

Huffman tree definition:

Huffman tree is also called optimal binary tree: the smallest binary tree in WPL

Construction method: merge the two trees with the least weight each time
Here we take the structure: 1 23 4 5 as an example

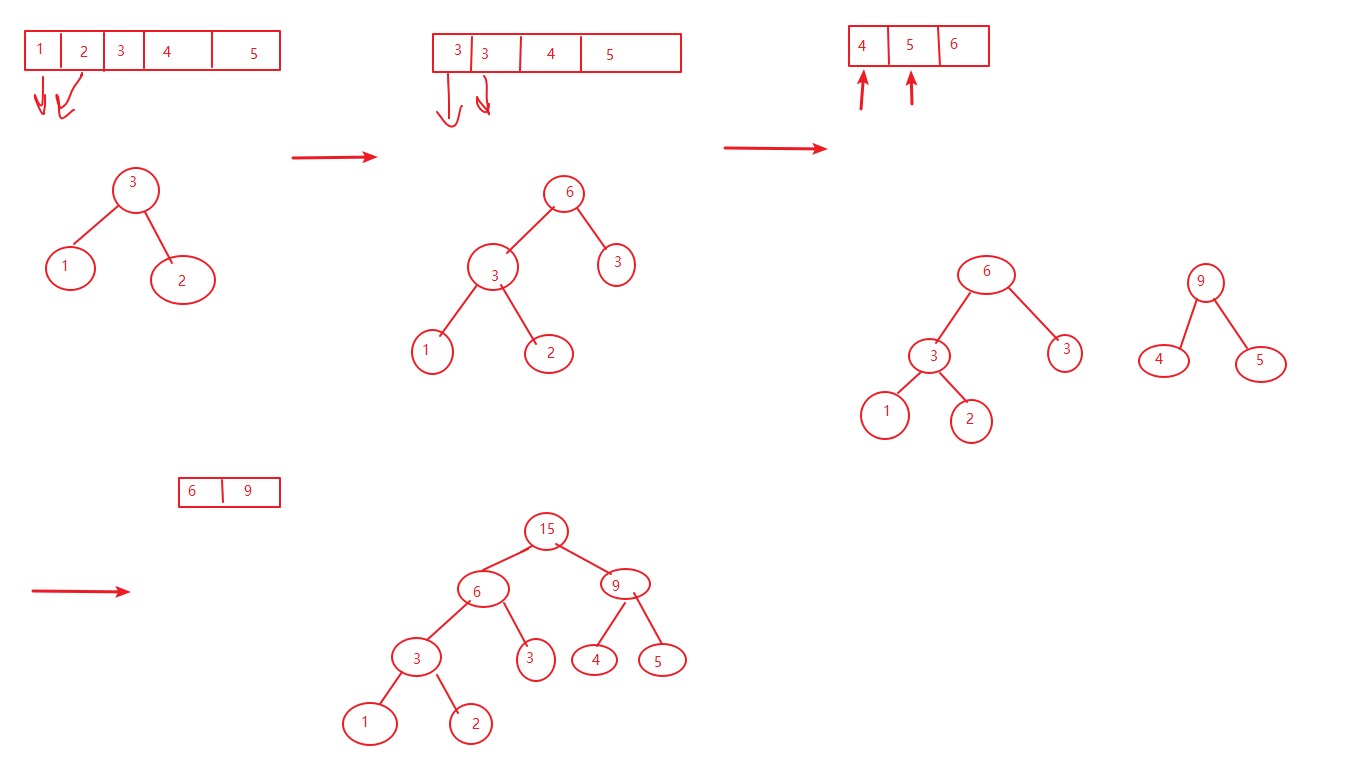Each time, we need to take two smallest elements out of a sequence, and then put a new element into it to form a new sequence. If we use an array, we need o (nlong) time for each sorting. If we use the smallest heap mentioned above to store data, insertion and deletion are o (logn) time complexity. This is done n times. The time to build a Huffman tree is O (nlogn), and if you use the array to sort every time, it is O (n^2logn).

Next, build a Huffman tree with the smallest pile.

#include <iostream>
#include <stdlib.h>

#define Maxn  1<<30 
using namespace std;

typedef struct Tree {
	int weight;
	struct Tree* left, * right;
}*BiTree, TreeNode;

#define ElementType BiTree 

typedef struct heapsturct
{
	ElementType* Elements; //At this time, the stored data should be the pointer of the tree node
	int Size;
	int Capacity;
}*MinHeap;


MinHeap Create(int MaxSize)//Create an empty maximum heap.
{
	MinHeap H = (MinHeap)malloc(sizeof(struct heapsturct));
	H->Elements = (ElementType*)malloc(sizeof(ElementType) * (MaxSize + 1));
	H->Capacity = MaxSize;
	H->Size = 0;
	BiTree T = (BiTree)malloc(sizeof(TreeNode));
	T->weight = -1 * Maxn;
	T->left = NULL;
	T->right = NULL;
	H->Elements[0] = T;
	return H;
}

bool IsFull(MinHeap H)//Determine whether the maximum heap H is full.
{
	if (H->Capacity <= H->Size)
		return true;
	else
		return false;
}


bool IsEmpty(MinHeap H)//Determine whether the maximum heap H is empty.
{
	if (H->Size == 0)
		return true;
	else
		return false;
}

BiTree DeleteMin(MinHeap H)//Returns the minimum element in H (high priority)
{
	if (IsEmpty(H))
	{
		cout << "The biggest pile is empty" << endl;
		return H->Elements[0];
	}
	ElementType item = H->Elements[H->Size--];
	ElementType value = H->Elements[1];
	int parent, child;
	for (parent = 1; parent * 2 <= H->Size; parent = child)
	{
		child = parent * 2;
		if (child < H->Size && H->Elements[child]->weight > H->Elements[child + 1]->weight)
			child++;
		if (item->weight < H->Elements[child]->weight) break;
		else
			H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = item;
	return value;
}

void PerDown(MinHeap H, int p) // The method of adjusting the node position to p is similar to that of deleting the maximum value 
{
	int parent, child;
	ElementType x;
	x = H->Elements[p];
	for (parent = p; parent * 2 <= H->Size; parent = child)
	{
		child = parent * 2;
		if (child < H->Size && H->Elements[child]->weight>(H->Elements[child + 1])->weight)
			child++;
		if (x->weight < H->Elements[child]->weight) break;
		else
			H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = x;
}


void BuildGeap(MinHeap H)
{
	int i;
	for (i = H->Size / 2; i > 0; i--)//Adjust one by one from the last parent node to the root node 1 
		PerDown(H, i);
}

void Insert(MinHeap H, BiTree item)//Insert the element item into the minimum heap H.
{
	if (IsFull(H))
	{
		cout << "Pile up" << endl;
		return;
	}
	int i = ++H->Size;

	for (; item->weight < H->Elements[i / 2]->weight; i = i / 2) // There is a small sentry at position 0. It ends at the top 
		H->Elements[i] = H->Elements[i / 2];

	H->Elements[i] = item;
}
BiTree Huffuman(MinHeap T)
{
	int n = T->Size;
	for (int i = 0; i < n-1; i++)
	{
		BiTree BT = (BiTree)malloc(sizeof(TreeNode));
		BiTree Min1, Min2;
		Min1 = DeleteMin(T);
		Min2 = DeleteMin(T);
		BT->weight = Min1->weight + Min2->weight;
		BT->left = Min1;
		BT->right = Min2;
		Insert(T, BT);
	}
	return DeleteMin(T);
}

void preTraverse(BiTree T)
{
	if (!T)
		return;
	cout << T->weight << " ";
	preTraverse(T->left);
	preTraverse(T->right);
}

void inTraverse(BiTree T)
{
	if (!T)
		return;
	inTraverse(T->left);
	cout << T->weight << " ";
	inTraverse(T->right);
}

int main()
{
	MinHeap H;
	H = Create(10);
	cout << "Insert element:";
	for (int i = 0; i < 5; i++)
	{
		int item = rand();
		cout << item << " ";
		H->Elements[++H->Size] = (ElementType)malloc(sizeof(TreeNode)); //Allocate space before using
		H->Elements[H->Size]->weight = item;
		H->Elements[H->Size]->left = NULL;
		H->Elements[H->Size]->right = NULL;
	}
	cout << endl;
	BuildGeap(H);
	BiTree  Root = Huffuman(H);
	cout << "Preordering:"; preTraverse(Root); cout << endl;
	cout << "Follow-up:"; inTraverse(Root); cout << endl;
}

The Huffman tree of random number given above is as follows: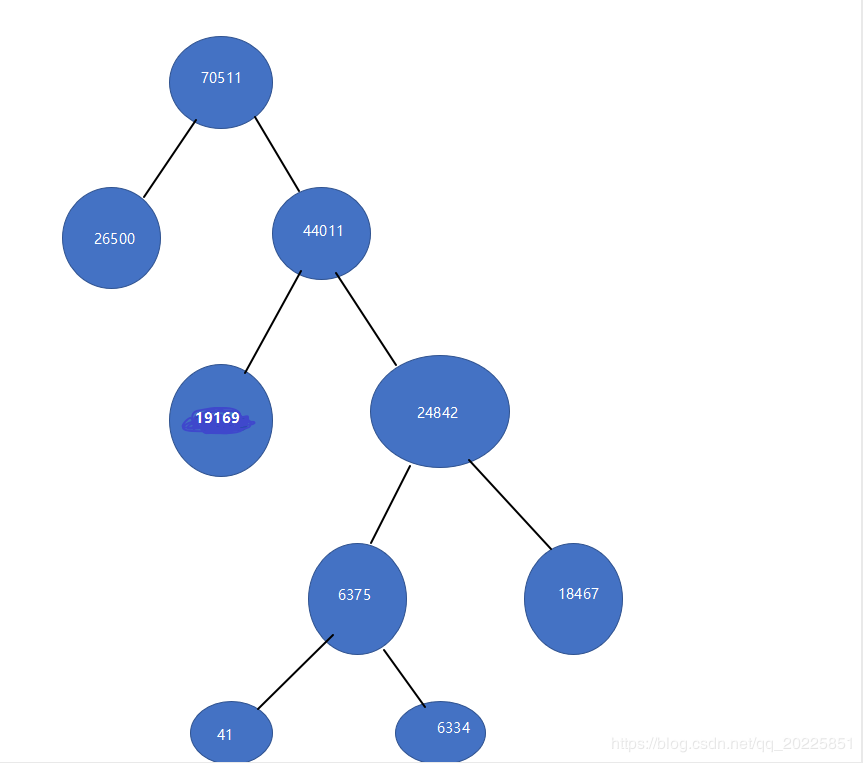

You can see that the smaller the weight, the greater the depth of the location. The greater the weight, the smaller the depth.

Huffman coding with Huffman tree above
Given a string and encoding the characters, the encoding storage space of the string can be minimized

Set up:
A number of times: 26500
B frequency of occurrence: 19169
C frequency of occurrence: 18467
D frequency of occurrence: 41
E frequency of occurrence: 6334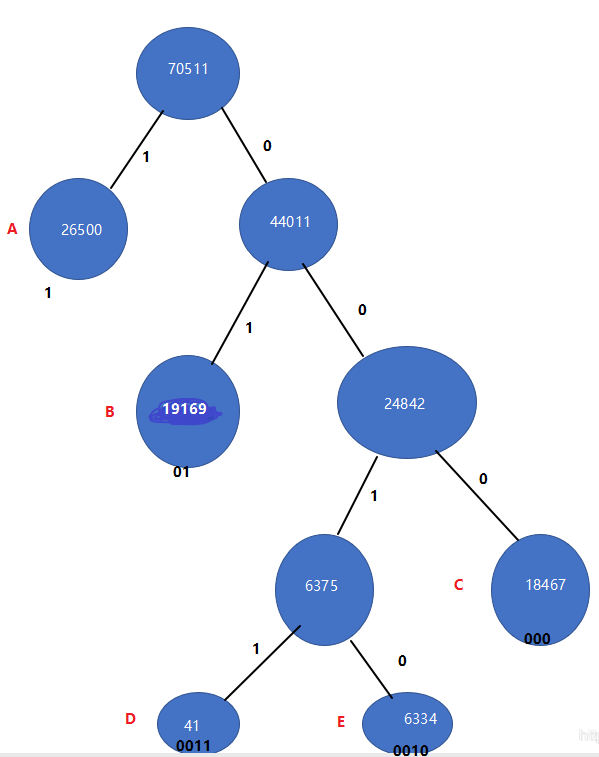

The corresponding code is
D ->0011
E ->0010
C ->000
B ->01
A ->1
Huffman code: cost = 126500 + 219169 + 318467 + 441 + 46334 = 145793
Equal length code: 3 (26500 + 19169 + 18467 + 41 + 6334) = 211533
ASSIC: 8*(26500+19169+18467+41+6334) = 564088
Through the above comparison of space use, we can see that using Huffman coding can greatly save space.

Specifically, I will implement it in the learning notes of Deng Junhui algorithm training camp, and directly use the priority queue in STL to replace the minimum heap to implement Huffman coding.

Set and operation

Set operation: intersection, union, complement and difference to determine whether an element belongs to a set
Concurrent query set: set merging, query what set an element belongs to

Using array to realize and look up set
Path uncompressed:

#include <iostream>

using namespace std ;
int find (int a[],int x)
{
	int root =x ;
	while (root !=a[root])
		root = a[root];
/*	while (root !=x)  //Path compression 
	{
		int item = a[x];
		a[item] = root ;
		x= item ;
	}
*/
	return item ;
}

void merge(int a[],int x1, int x2)
{
	a[find(a,x2)]=find(a,x1);
}

int main ()
{
	int a[11];
	for (int i=0;i<=10;i++)
		a[i] =i ;
	int n;
	cin >> n ;
	while (n--)
	{
		int x1 , x2 ;
		cin>> x1 >>x2;	
		if (find(a,x1)!=find(a,x2))
		{
			merge(a,x1,x2);
		}
	}	
	for (int i=0;i<=10;i++)
		cout << i<<"->"<<a[i]<<endl;
	return 0;
}

Connectivity without compression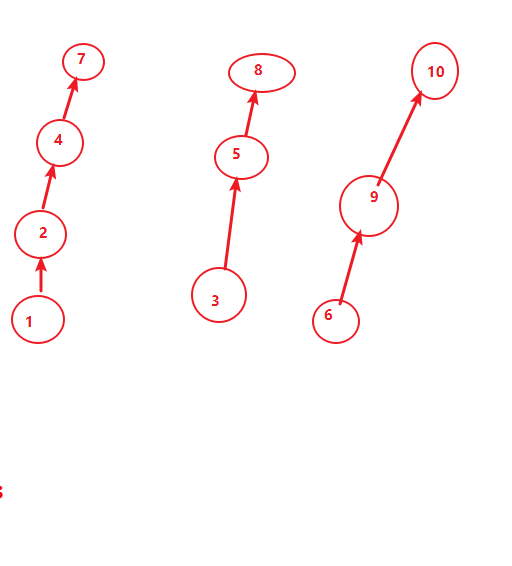

We can find that the path from 1 to 7 is too long, which will lead to a waste of too much time in finding the root, resulting in low efficiency of searching. If we compress the path and make the path shorter, the efficiency of searching will be much higher.

After compressing the path:

while (root !=x)  //Path compression 
	{
		int item = a[x];
		a[item] = root ;
		x= item ;
	}

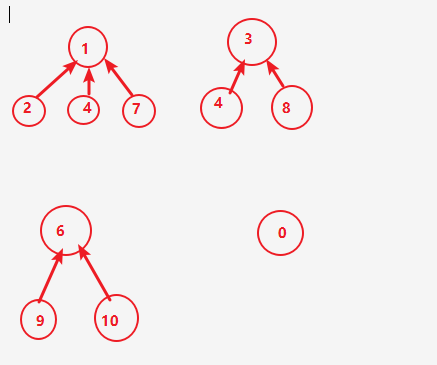
After the path compression, the paths become 1, which can improve the efficiency of parallel search.

Parallel search function

1. If the roots of two nodes are the same and the two nodes are connected, there must be a ring
2. You can judge whether two elements belong to the same class
3. How many kinds of judgments are there

##Exercise: path in heap 7-8##

Insert a series of given numbers into a small, initially empty top heap h []. Then, for any given subscript i, print the path from H[i] to the root node.

Input format:
The first line of each group of tests contains two positive integers n and M(< 1000), which are respectively the number of inserted elements and the number of paths to be printed. The next line shows the N integers in the interval [- 10000, 10000] to be inserted into a small, initially empty top heap. The last line gives M subscripts.

Output format:
For each subscript I given in the input, output the data on the path from H[i] to the root node in one line. Numbers are separated by one space, and there must be no extra space at the end of the line.

Enter an example:
5 3
46 23 26 24 10
5 4 3

Output example:
24 23 10
46 23 10
26 10

This problem can only be inserted while building a heap, can't use the method of saving data first and then building a heap, because it will change the output, which is inconsistent with the problem!

#include <iostream>
#include <stdlib.h>
using namespace std ;

typedef struct node{
	int date[1005] ;
	int size;
}*MinTree,Node;

void Insert (MinTree T , int item)
{
	int i = ++T->size ;
	for ( ; T->date[i/2] > item; i/=2)
		T->date[i] = T->date[i/2];
	T->date[i] = item ;
}

int main ()
{
	MinTree T ;
	T = (MinTree)malloc (sizeof(Node));
	T->size = 0 ;
	T->date[0] = -1*(1<<30);//Sentry
	int n , m ;
	int item ;
	cin >> n>> m;
	for (int i=1;i<=n;i++)
		{
			cin >> item ;
			Insert (T,item ); 	
		}

	for (int i=0;i<m;i++)
	{
		cin >> item ;
		cout << T->date[item];
		item /=2 ;
		while (item)
		{
			cout <<" "<<T->date[item];
			item /=2 ;
		}
		cout <<endl;
	}
	
		
	return 0;
} 

Exercise: 7-9 list connected sets

Given an undirected graph with N vertices and E edges, list all connected sets with DFS and BFS respectively. Suppose the vertices are numbered from 0 to N − 1. When searching, we assume that we always start from the vertex with the smallest number and access the adjacent points in the order of increasing the number.

Input format:
Input the first line to give two integers n (0 < n ≤ 10) and E, which are vertex number and edge number of graph respectively. Then line e, each line giving two endpoints of an edge. The numbers in each row are separated by 1 space.

Output format:
According to "{v"
​1
​​ v
​2
​​ ... v
​k
In the format of} ", each line outputs a connected set. First output DFS results, then output BFS results.

Input example:
8 6
0 7
0 1
2 0
4 1
2 4
3 5

Output example:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }

This problem I did not use and search sets, also did not use the heap, because the data is small, directly open two-dimensional array to save the relationship, and then directly deep search and wide search on it!

#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std ;

int a[11][11];
int Hash[11]; 
	int n, m ;
void dfs (int i)
{
	if (Hash[i]==0)
	{
		cout <<" "<<i;
		Hash[i] = 1;
		for (int j=i;j<n;j++)
		{
			if (a[i][j] ==1 && Hash[j]==0)
			{
				dfs(j);
			}
		}
	}	
}
int main ()
{
	memset(a,0,sizeof (a));
	memset(Hash,0,sizeof (Hash));
	cin >> n >> m ;
	int x1 , x2;
	for (int i=0;i<m;i++)
	{
		cin >>x1 >>x2 ;
		a[x1][x2] = 1 ;
		a[x2][x1] = 1 ;
	}
	for (int i=0;i<n;i++)
	{
		if (Hash[i]==0)
		{
		cout <<"{";
		dfs(i);
		cout <<" }"<<endl;
		}
	}
	memset(Hash,0,sizeof (Hash));
	for (int i=0;i<n;i++)
	{
		queue<int> q ;
		if (Hash[i] == 0)
		{
			cout << "{";
			q.push (i);
			while (!q.empty())
			{
				int item = q.front(); q.pop();
				if (Hash[item] ==0)
				cout <<" "<<item;
				Hash[item] = 1 ;
				for (int j=item;j<n;j++)
					if (Hash[j]==0 && a[item][j]==1 )
						q.push(j);
			}
			cout <<" }"<<endl;
		}
	}
	return 0;
}